预应力混凝土T梁桥非均匀收缩徐变效应分析

王 龙,邬晓光,张柳煜,莫 迪

(长安大学 公路学院,陕西 西安 710064)

0 引 言

近年来,预应力混凝土T梁桥得到了广泛应用,但也逐渐出现了大量病害。这些病害中,T梁腹板的竖向开裂现象尤为突出,但该现象所产生的机理尚不明确,这引起了学界的广泛关注。杨敏等[1]指出:一般力学观点无法很好地对该类裂缝所产生的原因进行说明。学界对典型病害的成因分析也较为宽泛,多是以施工质量及建材的收缩、温度等指标进行经验性地揭示,但没有从定性或定量角度进行具体分析。

环境温、湿度与混凝土收缩徐变发展密切相关。相对密封条件,干燥条件对混凝土试件的收缩徐变影响更大,会引起额外收缩及徐变变形[2-3]。由于干燥作用,水分扩散将使得混凝土内部产生明显的湿度梯度,内部收缩徐变特性随着位置变化而改变[4-5];其次混凝土内各部位配筋率亦存在差异,其约束作用也将使得梁呈现出非均匀收缩徐变效应。

为简化结构设计,收缩徐变特性通常采用均匀性假定[6]。V．KRSTEK等[7]认为:这种经典的简化假设在预测结构长期挠度及开裂时存在着误差。随着混凝土材料理论研究的不断深入,微预应力-固结(MPS)理论从微观角度推动了混凝土收缩徐变机理的发展[8]。该理论从温度、湿度变化的角度对混凝土收缩徐变进行分析,使得预测模型不仅适用于密闭、恒温条件下的基本徐变,也使得混凝土收缩徐变特征的分析更加准确合理[9]。LIANG Siming等[4]结合MPS理论获得了混凝土本征徐变特性参数,并得出了该参数仅与混凝土配合比有关,与加载和干燥条件无关的结论;王永宝等[10]和李传习等[11]分别采用梁单元对混凝土结构的非均匀收缩徐变效应进行了分析,但存在较多假定。

为了分析预应力混凝土T梁桥因非均匀收缩徐变效应给结构带来的影响,笔者基于微预应力-固结理论和纤维梁理论,提出了一种适用于预应力混凝土桥梁非均匀收缩徐变分析的纤维梁分析方法;该方法能综合考虑预应力混凝土梁因干燥收缩、徐变,温度变化,钢筋约束及预应力松弛产生的影响,能对预应力混凝土梁力学性能进行准确预测;并以某座预应力混凝土T梁为例,进行了数值分析,结合工程实例典型病害,验证该模型的正确性。

1 混凝土收缩徐变材料模型

1.1 混凝土内相对湿度预测

高原对[12]混凝土内部的相对湿度和混凝土收缩变形之间关系进行了研究和验证,认为混凝土收缩效应可进行更加精细地分析。湿度扩散模型可用于预测混凝土干燥收缩和自收缩[13]。通过FICK定律对混凝土内部湿度扩散进行计算,如式(1):

(1)

式中:H为混凝土内部湿度;Hs为自干燥引起的湿度变化;D(H)为湿度扩散系数;t为湿度扩散时间。

对于D(H),采用文献[14]所提出的预测函数进行计算,如式(2):

(2)

式中:D0为混凝土内相对湿度为100%时的D(H)值;α为D(H)的最小、最大值之比;Hc为当D(H)=0.5D0时混凝土内相对湿度;D0、Hc、α、β均为常数。

笔者采用文献[15]提出的水化自干模型对相对湿度增量和水化度增量进行计算,如式(3)、式(4):

(3)

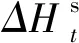
(4)

式中:Δαt为水化度增量;V0为平均水泥颗粒体积;ng为水泥颗粒数量。

收缩应变率可由式(5)计算:

(5)

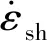
1.2 微预应力固结(MPS)理论

MPS理论能很好地预测混凝土短期和长期的收缩徐变性能,也能预测温、湿度变化下的混凝土收缩徐变行为。随着研究深入,MPS理论也得到了进一步发展,P．YU等[16]对MPS理论的模型进行了改进。故笔者采用文献[16]改进后的MPS理论进行研究。MPS模型示意如图1。

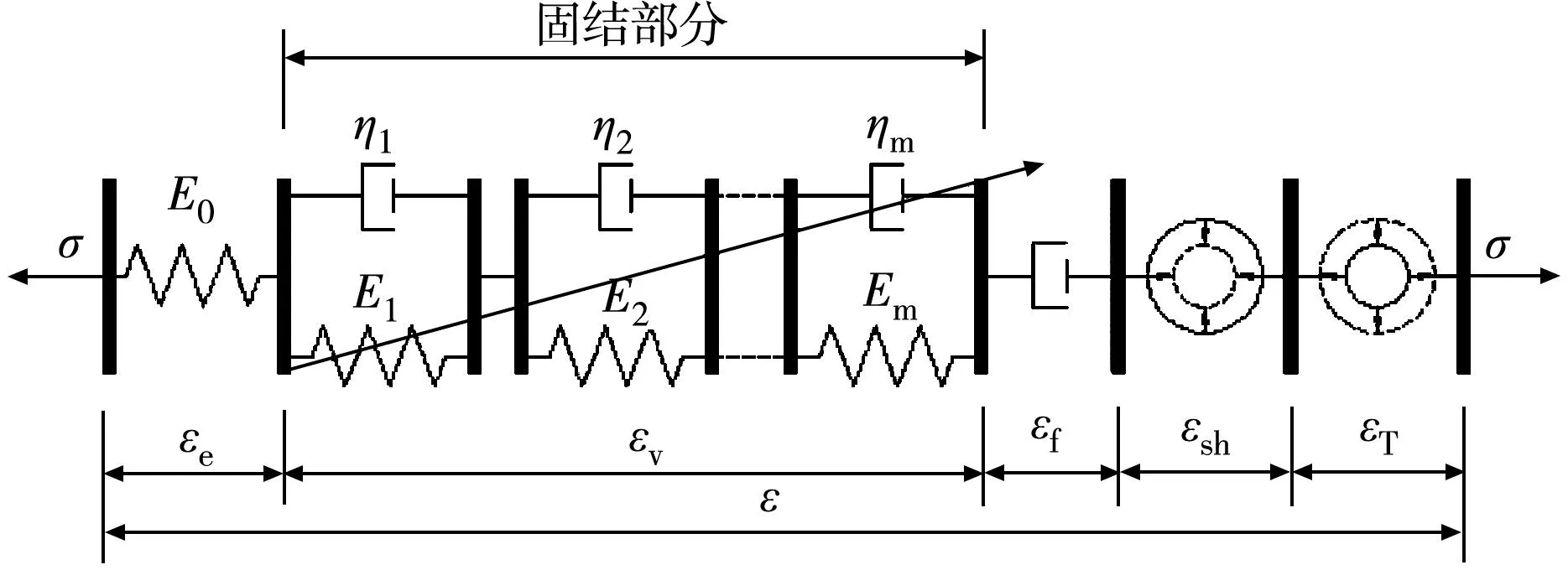
图1 MPS理论的流变模型

假定各应变线性可加,在单轴荷载作用下,总应变率可表达为各应变率之和,如式(6):

(6)

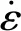
采用非线性增量格式有限元进行结构计算时[17],给定[Δεn+1],则混凝土应力增量与应变增量关系如式(7):

(7)

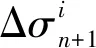
2 预应力材料松弛模型

预应力材料松弛主要与预应力材料种类、预应力张拉应力、张拉锚固工艺、锚固后持荷时间及锚固后预应力筋所处环境温度等5个因素有关[18]。在标准温度下,预应力钢绞线松弛的计算如式(8):

(8)

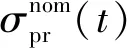
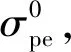
(9)

式中:Ep为预应力筋弹性模量,取常量。

3 非均匀收缩徐变纤维梁模型计算

3.1 截面及平均相对湿度

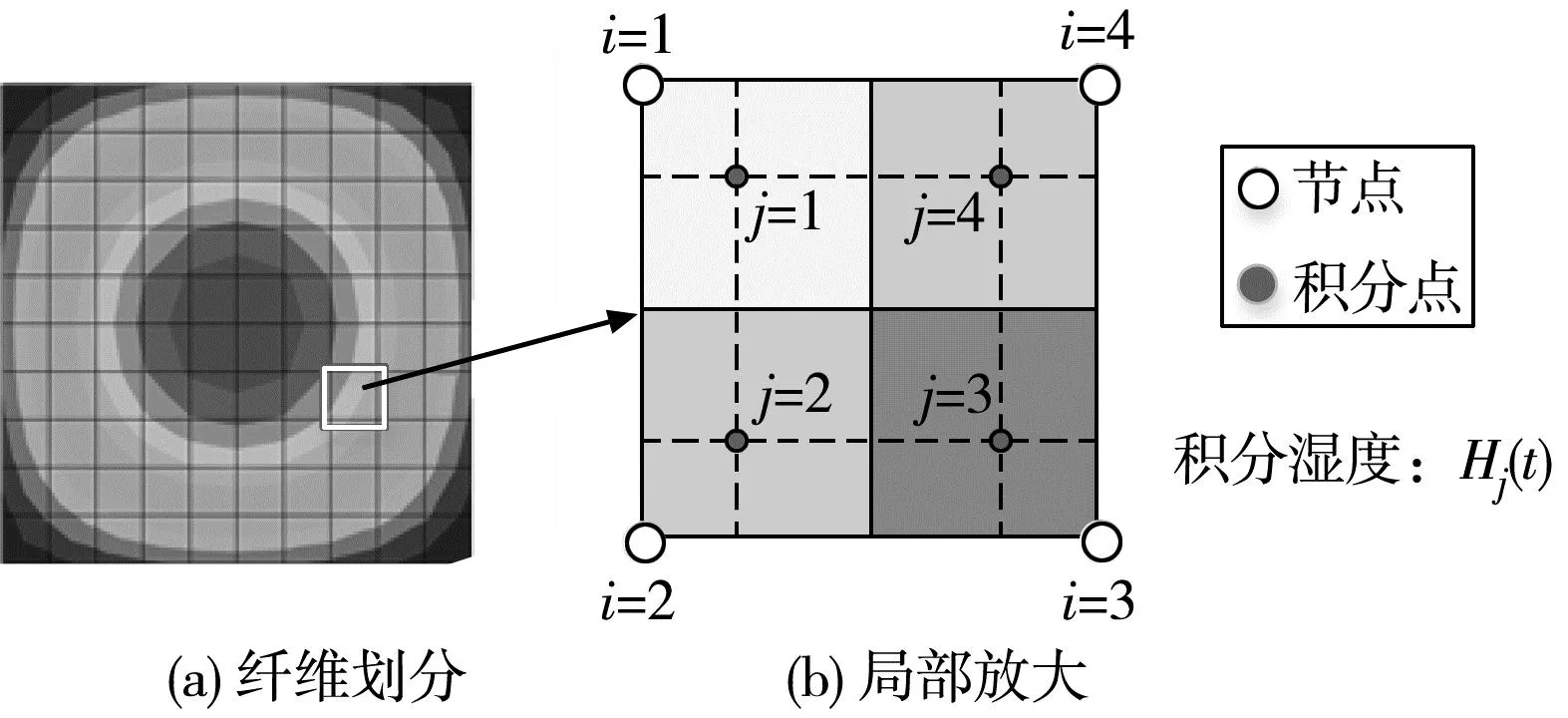
图2 截面纤维梁单元划分示意

(10)

3.2 二维二节点纤维梁单元

每个二维二节点纤维梁单元采用2个节点。每个单元节点具有3个自由度,图3(a)为单元示意,图3(b)为具体截面。梁单元积分点处截面特性计算包括混凝土、钢筋、预应力筋等3个部分。不考虑混凝土与钢筋的滑移,将混凝土截面划分为多个纤维单元,每个混凝土纤维单元拥有均匀特性;将钢筋及预应力筋考虑为单独纤维单元,忽略钢筋与预应力筋对截面剪切变形的贡献。截面特性计算如式(11):

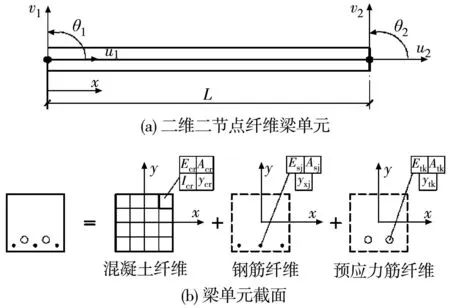
图3 二维二节点纤维梁单元及截面示意

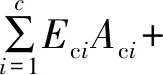
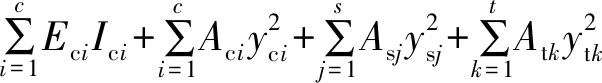
(11)

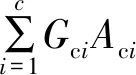
式中:Da为单元轴向刚度;Db为单元弯曲刚度;Ds为单元剪切刚度;Eci、Esj、Etk分别为各层混凝土、钢筋、预应力筋的弹性模量;Aci、Asj、Atk分别为各层混凝土及钢筋的面积;yci、ysj、ytk分别为混凝土层及钢筋层重心距离截面中性轴的距离;κ为剪应力分布不均匀常数,对于矩形截面,κ=5/6;Gci为混凝土剪切模量。

3.3 非线性增量格式有限元

利用增量法构建非线性有限元计算过程。将计算的整个时域T分割为n份,每个时间节点为t0=0,t1,t2, …,tn,tn+1,tk=T。在指定时间步内[tn,tn+1],tn时刻节点位移为qn,则各高斯积分点的应力σn、应变εn均已知。梁单元不平衡力[20]的计算如式(12):

(12)

式中:R(e)为节点不平衡力向量;F(e)为等效节点外荷载向量;B为梁单元应变矩阵。

4 实例分析

取一片30 m等截面简支预应力混凝土T形梁,其布置如图4,T梁截面如图5。T梁梁高200 cm,顶板厚度18 cm,腹板厚度20 cm,马蹄50 cm,尺寸差异较明显;T梁上设10 cm桥面混凝土和10 cm沥青混凝土层,两层之间设置防水层;普通钢筋主要为HPB300、 HRB400级,预应力筋采用高强低松弛钢绞线,在梁底直线布置,抗拉强度设计值为1 860 MPa。假设T梁在3 d时脱模处于干燥环境中,在7 d时张拉预应力钢绞线,67 d时完成桥面铺装。

图4 T梁布置(单位:m)

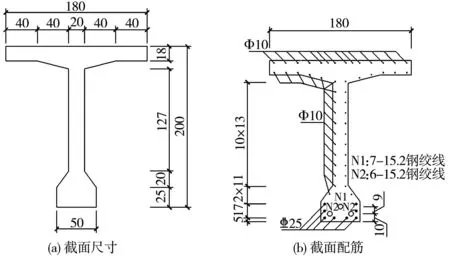
图5 T梁截面

在干燥条件下,T梁顶板、腹板、马蹄收缩徐变特性具有较强的尺寸效应,由于非均匀收缩徐变效应,梁体将发生挠曲。由图5可知:顶板、腹板、马蹄配筋率分别为0.92%、0.28%、3.23%,普通钢筋对截面不同部位混凝土收缩徐变的约束作用不同,会加剧其效应。

4.1 截面湿度分析分及纤维梁单元划分

笔者取常规混凝土进行分析,混凝土水灰比为0.34,集料比为4.15,水泥平均细度为380 m2/kg,水泥颗粒平均粒径为12.5 μm。根据文献[12-13],选取相应模型参数如表1。

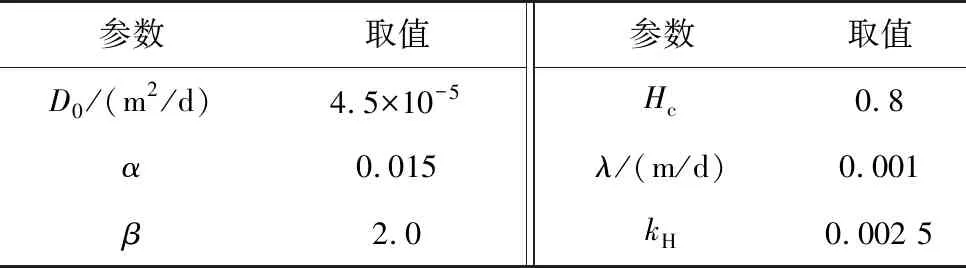
表1 混凝土湿度扩散模型参数

在结构计算中,通常不考虑桥面铺装层混凝土参与受力,但由于桥面铺装层存在,T梁顶面温度及干燥边界会发生变化。在截面湿度扩散过程中,由于桥面铺装(含防水层)将有效阻碍T梁顶面的干燥失水。笔者对两种干燥工况进行研究,工况1:T梁截面完全暴露于60%环境的相对湿度下;工况2:当完成桥面铺装时,将顶面定义为绝湿边界。500 d时T梁截面相对湿度分布如图6。

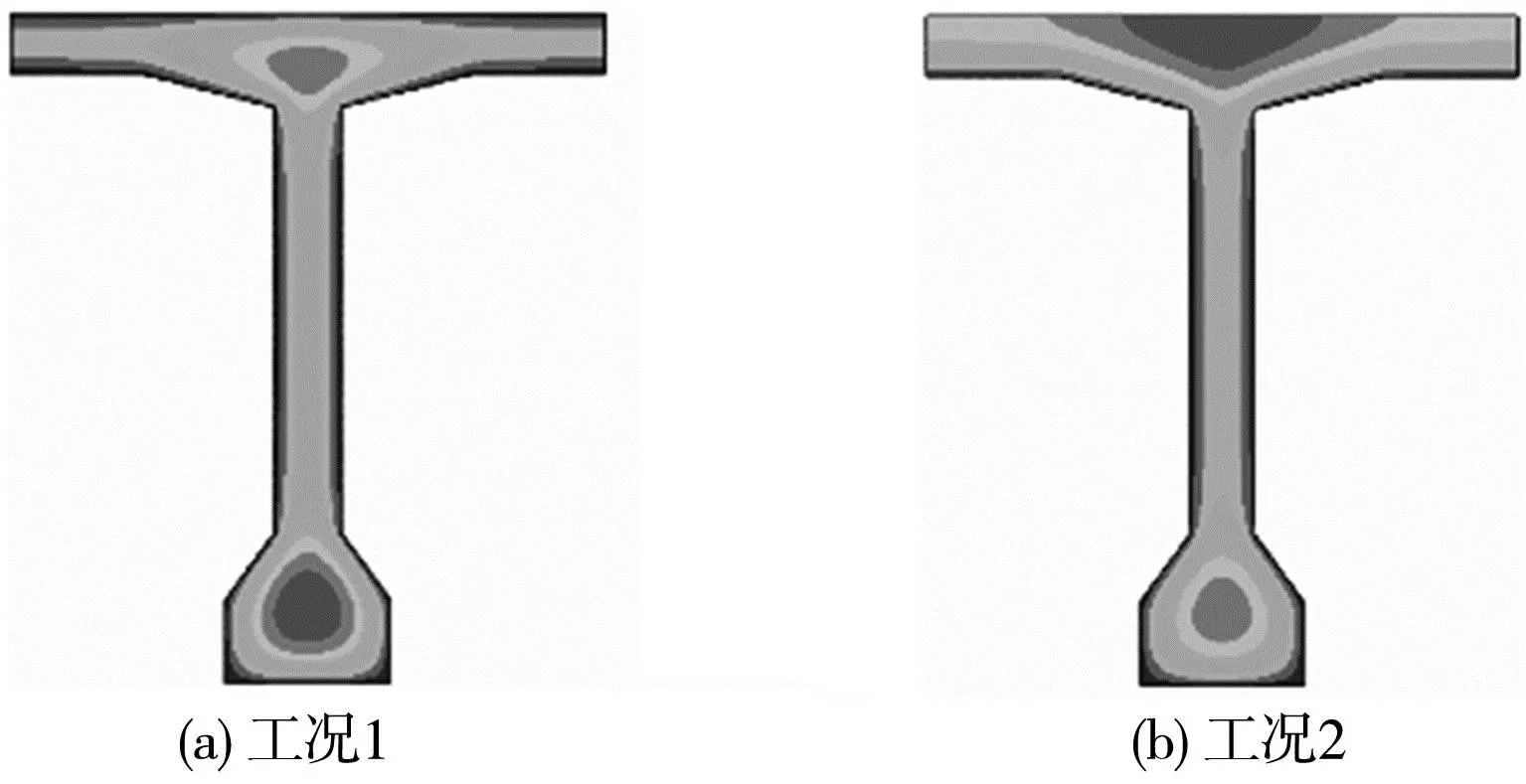
图6 T梁截面湿度分布

由图6可知:当顶面干燥条件发生变化时,T梁顶面的湿度分布规律变化十分显著。若不考虑桥面铺装影响,顶板湿度有较好类似“板”的分布规律,湿度核心区较小;若顶面干燥过程受到阻碍时,干燥面积减少一半,顶板水分只能向下表面扩散,形成较大的湿度核心。根据MPS理论,湿度是影响混凝土材料收缩徐变特性的重要参数之一,截面湿度分布规律对结构受力性能有着至关重要影响。

工况1:根据截面湿度分布规律,将截面划分为多个纤维梁单元,如图7。将截面划分为11个纤维(图8)或96纤维梁单元,可降低均匀假定带来的误差。

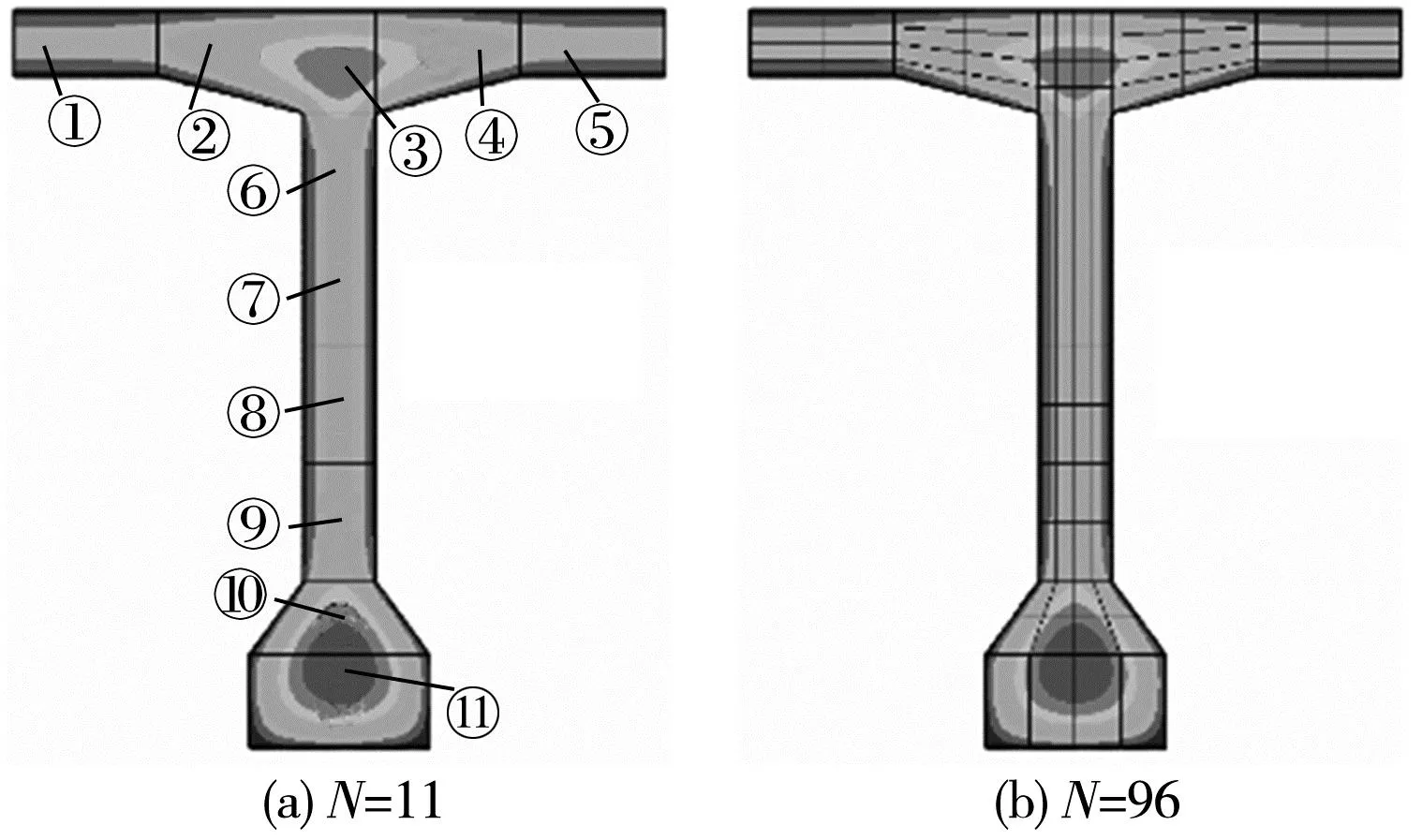
图7 T梁截面划分

图8 N=11时各纤维平均相对湿度随时间变化(工况1)

由图7、图8可知:T梁截面内各纤维平均相对湿度存在较大差异,T梁翼缘板较薄(纤维1),湿度下降最快,腹板(纤维6～9)次之,顶板与腹板铰接处(纤维3)和马蹄(纤维10～11)较厚,湿度下降速率远低于其他部位。不同时刻各纤维材料的特性不同,将各纤维进行编号,求解后则可得到任意一纤维的结果,纤维划分越多,结果越精细。

4.2 预应力混凝土T梁非均匀收缩徐变效应

根据改进的MPS模型及预应力松弛模型,预应力混凝土T梁结构计算参数如表2。

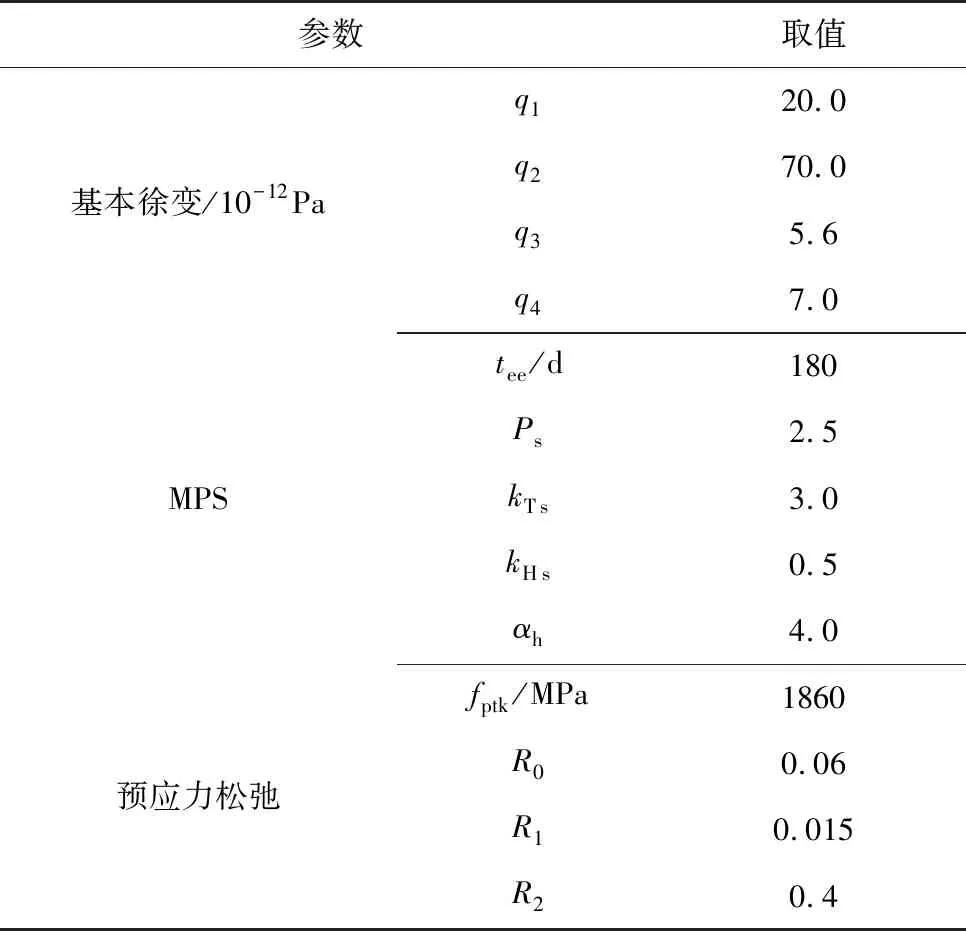
表2 结构分析参数

为简化计算,忽略预应力因管道摩擦、锚固等造成的瞬时损失,假定梁底预应力筋初始应力均为1 395 MPa。当N=11时,T梁跨中挠度随时间变化如图9。

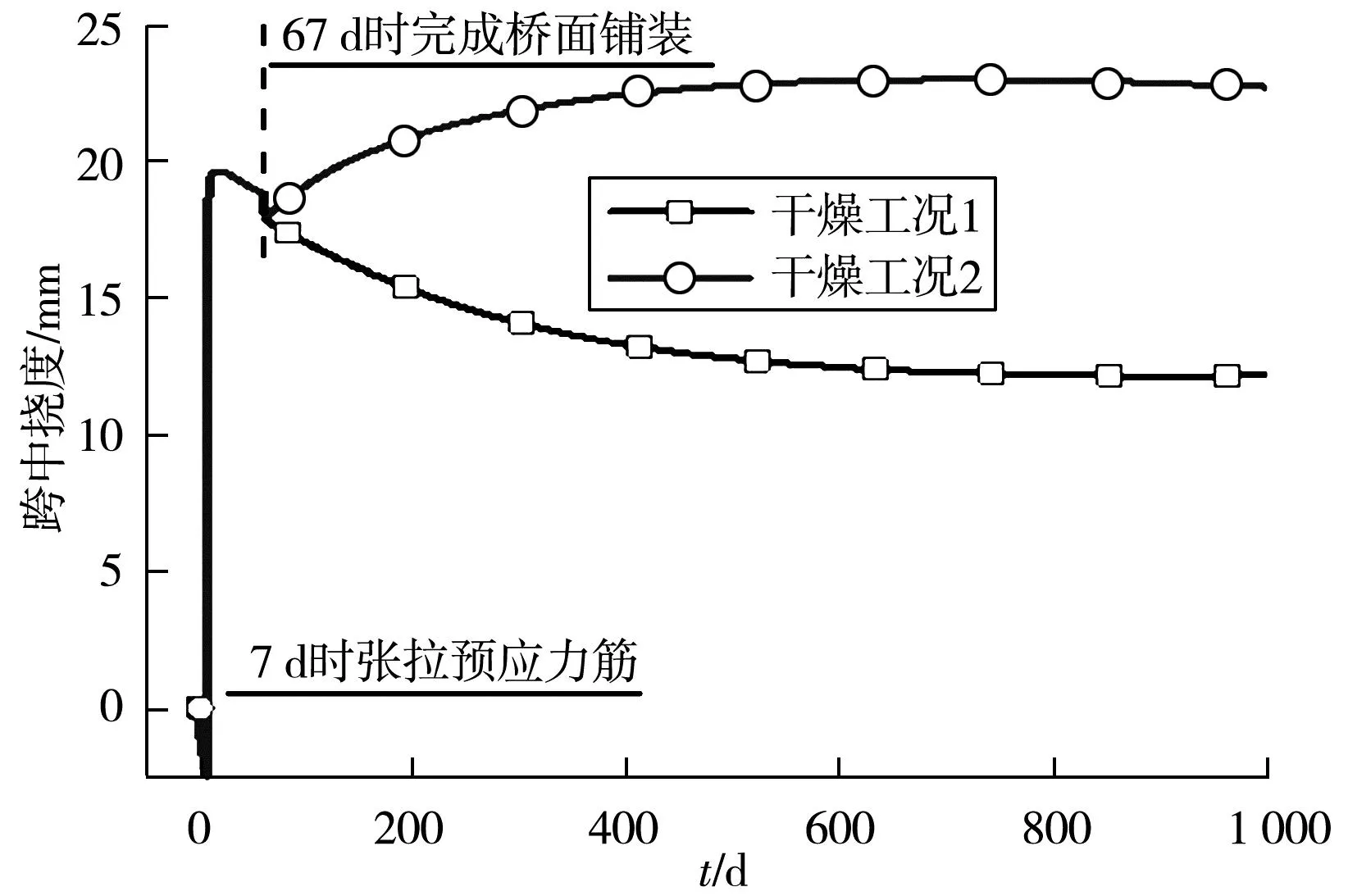
图9 跨中处挠度随时间变化

由图9可知:当截面处于干燥条件时,对结构变形及应力分布均有较大的影响。工况1中,顶板(纤维1～2)湿度的下降速率(收缩速率)大于腹板和马蹄,马蹄配筋率高于顶板和腹板,由于各区域收缩徐变速率及钢筋约束作用强弱不同,梁体因干燥产生向下的挠曲;工况2中,T梁顶板干燥受到桥面铺装限制,T梁顶板湿度下降速率将明显低于腹板和马蹄,梁体因干燥产生的挠曲与工况1相反。

7 d张拉完预应力筋后,梁体处于上拱状态,完成桥面铺装后,T梁干燥条件发生变化,梁体挠度发展趋势呈现相反趋势,如图10。由图10可知:纤维梁单元能有效反应预应力筋应力随时间变化的规律,预应力筋的应力早期下降迅速,后期逐渐趋于稳定。随着T梁收缩徐变及预应力筋松弛发展,预应力筋内有效预应力在持续下降,在1 000 d时,有效预应力下降至约83%,由于干燥条件改变了混凝土材料力学性能,不同工况下的预应力筋有效预应力亦存在差异。

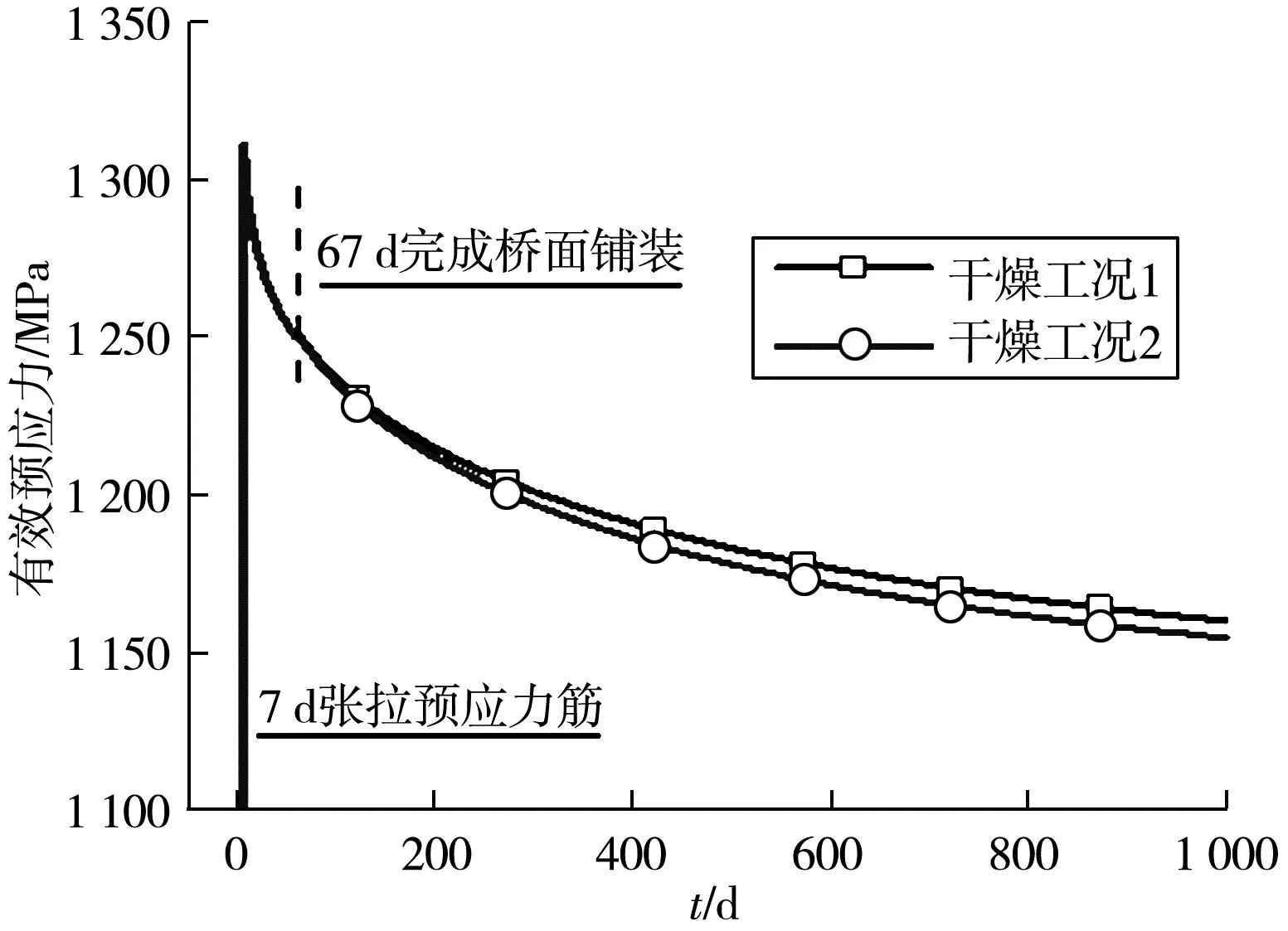
图10 跨中处N1预应力筋有效应力随时间变化

在干燥及混合配筋约束作用下,结构内部应力分布将产生较大的不均匀性,如图11、图12。在1 000 d时,在自重及预应力共同作用下,截面仍处于全受压状态;在多种因素共同作用下,各区域压应力储备存在明显差异。工况1中,马蹄处压应力较高(-2.3 MPa),顶板压应力次之(约-1.8 MPa),而翼缘板和腹板是薄弱部位(约-1.0 MPa);工况2中,应力分布不均匀性更为显著,梁体荷载主要集中于顶板及马蹄部位(约-2.2～-3 MPa),腹板部分区域压应力仅为-0.1 MPa。

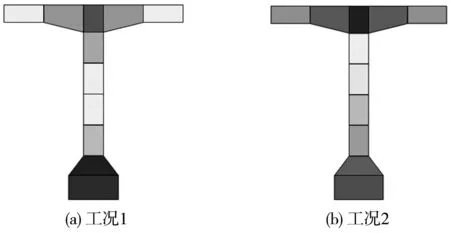
图11 1 000 d时跨中截面应力分布

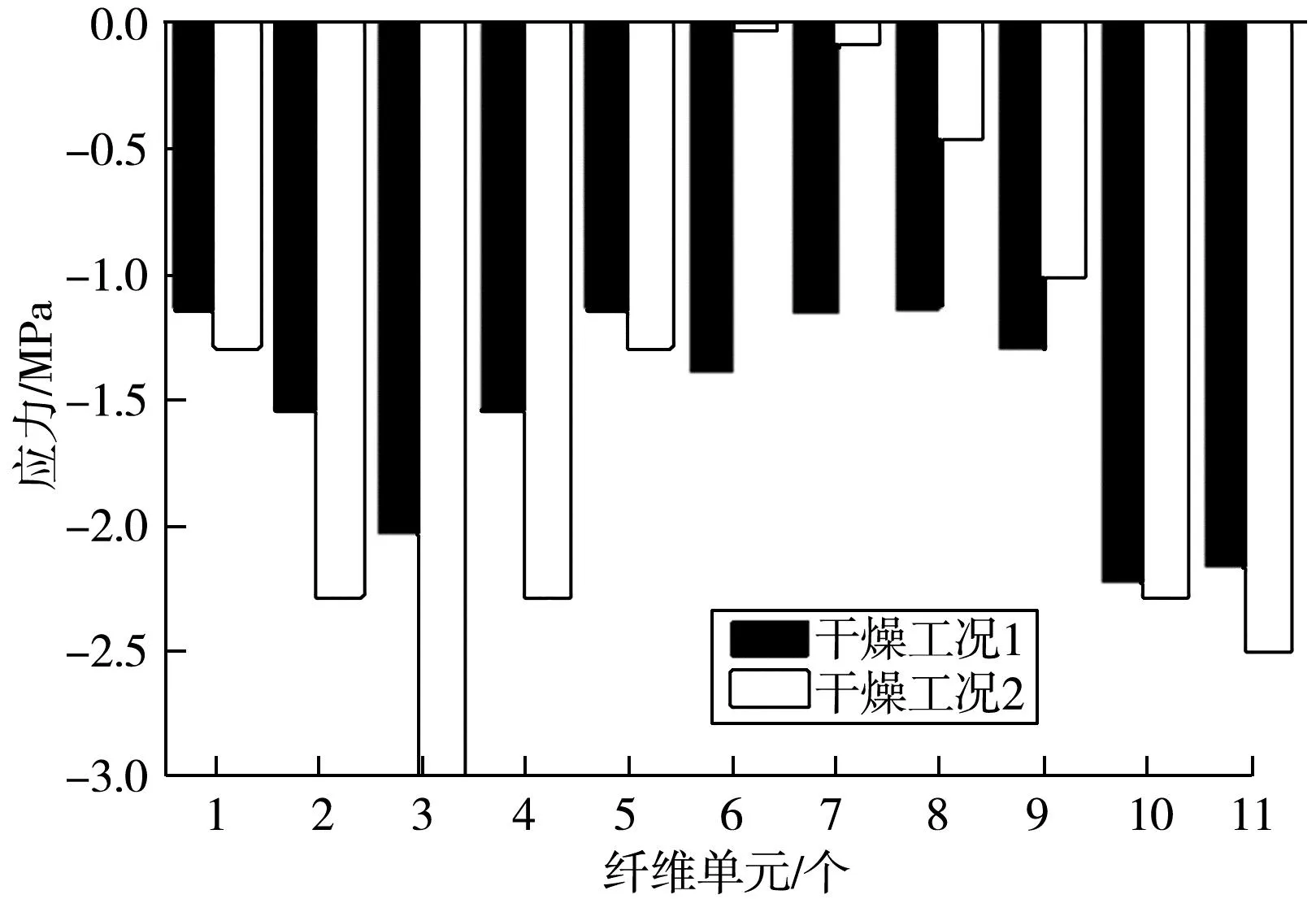
图12 跨中截面处各纤维形心处应力

T梁容易在跨中区域(梁体L/3～2L/3之间)产生腹板两侧对称的竖向裂缝,部分线路预应力混凝土T梁腹板竖向开裂比例为38.64%(桥梁比例高达82.69%)。跨中区腹板竖向裂缝如图13。裂缝仅发生于T梁腹板区,根据芯样,裂纹已完全贯穿腹板。由图13可知:仅在自重及预应力荷载作用下,T梁跨中区域腹板压应力储备显著低于顶板及马蹄部位,腹板是应力薄弱部位,T梁病害与腹板应力薄弱部位吻合,非均匀收缩徐变为该类裂纹产生的重要因素。

图13 T梁跨中区腹板竖向裂缝

4.3 纤维数量影响

当N=96时,T梁挠度及预应力松弛结果与N=11时一致。但应力计算结果存在较大差异,1 000 d时跨中截面应力分布如图14、图15。截面应力分布不均匀不仅存在于T梁竖向中,各部位内外侧也存在差异。由于干燥作用,混凝土表面及内部会因非均匀收缩徐变产生自平衡应力。混凝土干燥早期,表面混凝土干燥较快,混凝土收缩及老化显著,表面混凝土处于拉伸状态,内部混凝土将处于受压状态进行平衡。随着表层混凝土完全干燥,表层混凝土收缩及老化速率将低于内部混凝土,伴随着老化过程中不可逆徐变部分εf的累积,将导致应力分布反转,使得表层混凝土处于受压,内部处于受拉状态。1 000 d时,由于非均匀收缩徐变作用,腹板外侧压应力略高于腹板内侧,在所选参数下,腹板内外应力相差约1 MPa;工况2中,腹板内产生0.7 MPa拉应力。

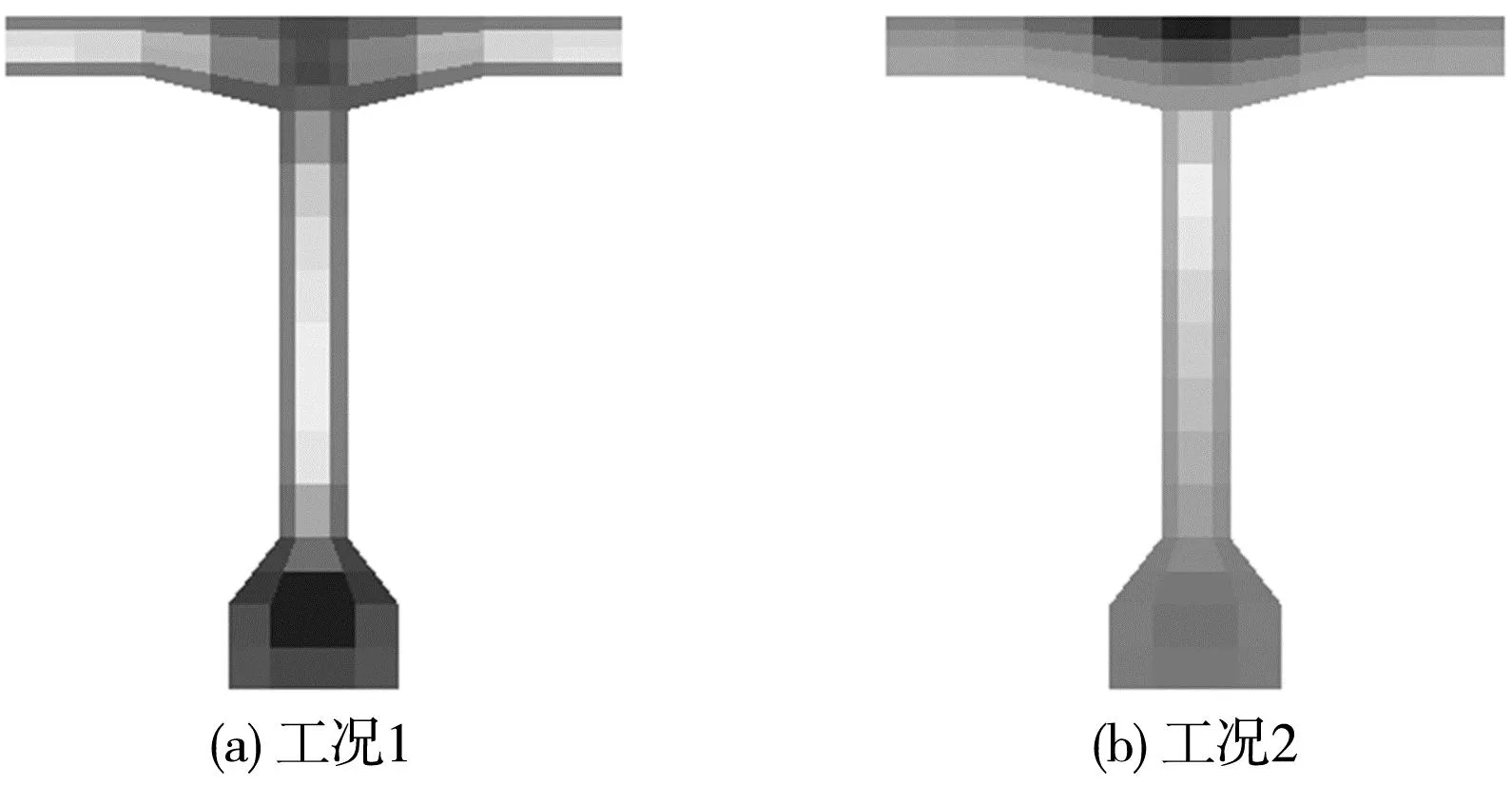
图14 1 000 d时跨中截面应力分布

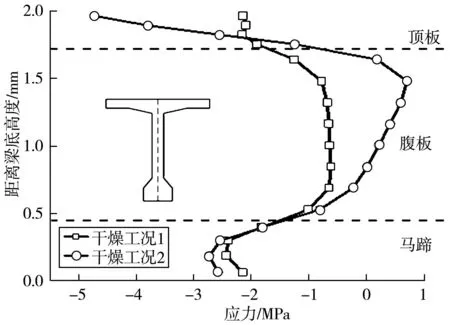
图15 截面中心应力分布

5 结 论

为计算预应力混凝土T梁桥非均匀收缩徐变效应对结构的影响,笔者结合纤维梁理论和微预应力-固结理论,提出了一种纤维梁分析方法。根据计算分析,该模型具有良好的稳定性及收敛性;能综合考虑预应力混凝土梁因干燥、收缩、徐变、过渡热徐变、钢筋约束及预应力松弛等产生的影响,可对预应力混凝土梁力学性能准确预测。根据分析,得到如下结论:

1)结合MPS理论,纤维梁单元可分析任意对称截面预应力混凝土梁力学性能。与传统分析相比,能更加精细地分析在非均匀收缩、徐变、混合配筋下预应力混凝土梁的各项力学指标;

2)平均相对湿度具有良好的代表性,且干燥条件对预应力混凝土T梁非均匀收缩徐变存在显著影响;

3)在混合配筋及干燥条件下,预应力混凝土T梁非均匀收缩效应显著,在传统均质梁分析过程中不能反映该效应对T梁的影响,使得梁体在设计过程中存在薄弱部位;

4)对于尺寸较复杂的T梁截面,由于收缩徐变尺寸效应,不仅各个部位(顶板、腹板、马蹄)将产生较大自平衡应力,每个部位内外亦会产生自平衡应力,应予以充分考虑。