碳配额交易约束下供应链决策问题研究

任 帅

(兰州交通大学交通运输学院 兰州 730070)

0 引言

近年来,由于全球气候变暖和环境污染,环保已成为当下主流话题。我国很早就提出了节能环保的口号,推行节能环保的政策,在国家大力推动可持续发展的同时,民众的环保意识也在不断地提高。对于同样的产品,民众的消费理念由原来的物美价廉转变为低碳节能,甚至在相同的条件下,部分消费者愿意以更高的价格去购买低碳节能的产品。消费者低碳消费偏好会对厂商的生产和定价产生很大的影响,因此,考虑消费者偏好的库存管理决策是值得进行深入研究的领域。

楼高翔等[1]没有将消费者的偏好作为供应链的共有信息,而是将其作为零售商的私有信息,在这种情况下,研究分析了供应链在生产环节的碳减排技术的投资和供应链激励机制设计等方面的相关问题,对政府在碳权交易等方面提出了相关的政策和建议。刘名武等[2]将碳交易约束机制和消费者对低碳产品的偏好都考虑进来,在两级供应链中,从生产商的碳减排技术成本投入与合作的环节入手,构建了动态优化模型,采用微分博弈的方法,求解分析,证明了生产和使用两个环节中的碳排放纳入碳交易之中可以促进碳减排。Yalabikb等[3]研究了在企业的竞争、政府制定的碳减排法规以及最下游的消费者需求等影响下制造商的最优决策问题。Turaym[4]在传统的企业EOQ订货模型中加上了环境标准,分别分析了碳税、碳限额交易和碳补偿三类碳约束政策在企业的碳减排中起到的作用。Hua等[5]在经典的EOQ订货模型之中纳入了碳交易政策,并将该模型与传统的EOQ经济订货模型放在一起,进行了比较分析。Battini等[6]分析了供应链运作过程中哪些因素可以影响整个过程中碳排放量大小,并将相关因素进行集成和量化处理,构造可持续的EOQ订货模型。Hocelaque等[7]在传统EOQ订货模型的基础上考虑订货量和库存对厂商的运作过程中碳排放量的影响。王芹鹏等[8]假定企业考虑消费者的低碳偏好,并为此自愿做出努力,进行碳减排时,在单个供应商和单个零售商组成的二级供应链中,研究零售商的最优订货决策问题和供应商的最少碳排放量决策问题。李林等[9]在存在竞争的市场之中还考虑了消费者的低碳偏好和产品的价格影响,研究这两种行为特征在供应链上下游的绿色活动中如何来影响供应链的绩效结果和利润的分配。姚凡军等[10]在碳配额交易政策下,从碳排放的长期和短期的效应出发,研究在消费者的低碳消费偏好下对零售商的收益和决策的影响。冯瑛杰等[11]从现实中机票、酒店服务等易逝产品的定价出发,在考虑消费者的消费者行为和风险偏好的差异的基础之上,研究供应链中的双阶段定价问题。

通过对上述研究进行梳理,可以看出,消费者的低碳偏好对供应链的影响已有很多人在进行研究,并取得了不错的成果。消费者的低碳偏好会对供应链的决策产生影响,从而影响整个供应链的生产、定价和收益。因此,在上述研究的基础上,考虑由生产商拥有和管理的单一项目库存系统。在生产商生产产品和向下游发货的过程中都会产生成本,持有产品也会产生成本。考虑到当前的低碳目标和消费者的低碳偏好,将碳排放进行量化,将各个过程的碳排放量统计出来,根据碳限额约束机制,将碳排放量和消费者的低碳消费偏好都纳入模型之中,探讨研究生产厂商的利润最优时的周期生产决策和产品的定价决策。

1 问题描述与模型构建

1.1 市场需求

假设市场的规模需求为Q,消费者对碳排放量和产品价格的敏感系数为a,b(a,b>0),p为产品的价格,从产品生产出来开始到发送到消费者购买产品为止,基本每个环节都会产生碳的排放。研究中假设每储存单位产品的碳排放量是g1,生产每单位产品的碳排放量为g2,运输过程中的单个产品的碳排放量为g3,g是单位产品的总碳排放量,其他环节的碳排放量均忽略不计。市场的实际年需求是:D=Q-ag-bp,单个周期内的生产量为q,那么生产次数n=D/q,为简化计算每年按360d算,那么单个生产周期的时间t为:

(1)

1.2 成本分析

持有成本(C1):单位时间内每件产品的持有成本是h[12],假设客户的需求与时间是线性关系,单个生产周期的生产量为q,仓库在整个生产周期内的平均库存为0.5q,库存时间为t,那么单个周期内厂商的库存持有成本为:

(2)

运输成本(C2):运输过程中运输每单位商品的成本是d,运输成本为:

C2=dq

(3)

生产成本(C3):生产厂商每次的固定生产成本为F,单个产品的生产成本为w,周期内的总生产成本为:

C3=F+wq

(4)

1.3 收益分析

碳收益(CP):研究的碳约束选用碳配额约束机制,政府给每个企业单位的碳排放量都有一个规定额度,一旦企业在生产经营的过程中产生的碳排放总量超过了政府给该企业规定的限额,那么企业需要从碳交易市场去购买碳排放额度,满足自己的碳排放,如果该企业生产经营完成后还有多余的碳排放额度,该企业也可以在碳交易市场进行交易[13]。政府给生产商规定的碳排放额度为G,碳交易市场碳排放额度的价格r,则碳收益为:

CP=(G+qg)×r

(5)

生产商每个生产周期内的总利润为:

TP=(pq+CP)-(C1+C2+C3)

(6)

1.4 建立模型

碳约束下基于消费者偏好的生产商生产—库存利润模型为:

(7)

2 模型求解

构建了碳约束下基于消费者偏好的生产商生产—库存利润模型,用数学分析法验证构建的模型有没有最优解。首先,判断碳约束下基于消费者偏好的生产商生产—库存利润模型函数的凹凸性。可以通过函数的单调性来判定,构建Hessian矩阵判断模型函数的凹凸性。Hessian矩阵的构建如下所示,如果函数的Hessian矩阵负定,那么该函数就有极值,否则就没有极值。

(8)

矩阵中各二项偏导数为:

(9)

(10)

(11)

解得当720hqb>(Q-ag-bp)2时有Δ恒>0,此时Hessian矩阵负定,该函数有极大值,该模型有最优解。

令一阶偏导数为0:

(12)

(13)

连立二式解得:

(14)

(15)

若720hqb<(Q-ag-bp)2则不满足极值条件,此时函数没有极值,该模型也就没有最优解,只讨论存在最优解的情况。

碳配额与碳交易价格对厂商决策的影响:

(1)单位产品的总碳排放量为g,那么整个过程中碳排放量qg若大于碳配额G,那么可交易的碳配额为负,需要购入碳配额来满足自己的碳排放,那么碳收益为负;如果总的碳排放量qg小于碳配额G,那么就有多余的碳配额去交易,碳收益为正。

(2)根据计算结果可知,产品的价格p与碳交易价格r成正比,与消费者的碳排放敏感系数成反比,生产量q与产品价格p成反比;若碳交易价格为0,则表示对碳排放政策对厂商没有约束,此时产品的价格与碳排放量g成反比,生产量q与产品的碳排放量g成正比。

(3)企业分配的碳配额的大小不会影响厂商的定价决策和生产决策,但是却会影响利润的大小,碳配额越大,碳收益越大,厂商的利润也就越大。

3 算例分析

根据性质2可以看出消费者对碳排放量的敏感系数a对生产决策和定价决策都有影响,因此,在算例分析中主要对研究消费者对碳排放量的敏感系数a的影响。给第三部分构建的模型赋值:某产品的下游市场的规模需求为500件,下游的消费者对该产品的价格敏感系数为10(产品定价每增加1元,市场的需求减少10件),需求函数为:D=500-ag-10p,生产过程中生产一件产品就会产生碳排放量0.6kg,储存过程中每单位产品的碳排放量为0.2kg,运输过程中单位产品的碳排放量为0.2kg,单个产品的生产成本为8元,每次生产的固定成本为200元,政府给该企业的碳配额为300kg,碳交易市场的价格为10元/kg,运输单位产品的运价为0.2元,库存持有成本为0.2元。下面研究不同的a值下市场需求、定价决策、生产决策和厂商的利润有何变化。具体变化如表1所示。

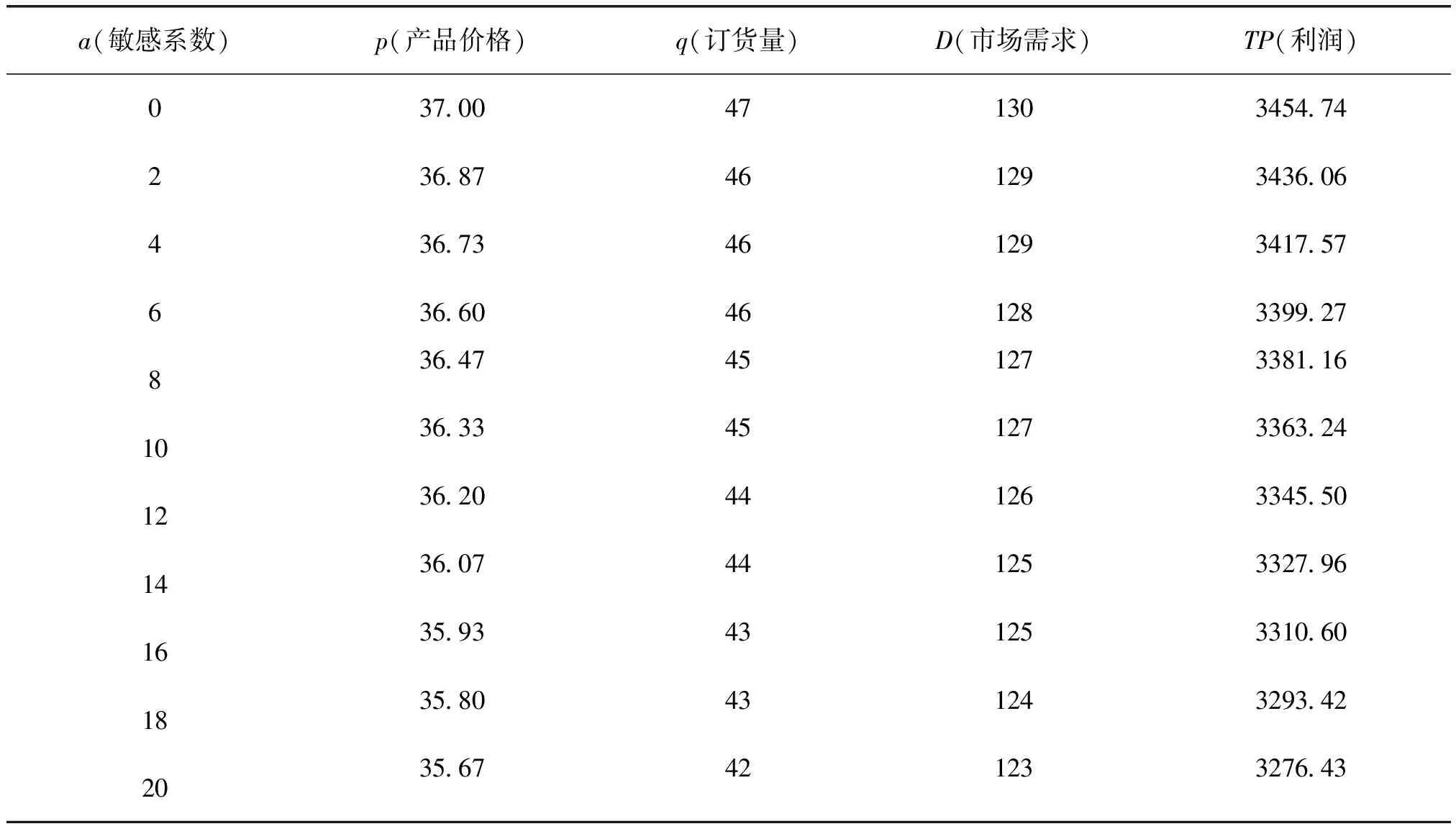
表1 消费者对碳排放量敏感系数的变化对产品价格、订货量、市场需求和利润的影响

根据表1可以看出:

(1)产品的价格随a值变化的幅度较小,变化区间不大,变化幅度在(39.5～38.0)之间,原因是消费者的碳排放敏感系数越大,说明消费者更加注重产品的环保性,消费者对价格的敏感性也会相对下降。

(2)市场需求的变化范围在(99,106)之间,这是因为a值变大,说明消费者对环保的要求更高了,人们追求碳排放量更低的产品了,这会导致产品的市场需求下降。

(3)a值对生产量的影响也不是很大,对q值向下取整,周期内的生产量的变化范围在(27,31)之间,这是因为随着a值的变化,总的市场需求下降了,那么单位周期里的生产量也会减少。

(4)a值对利润的影响是最大的,利润的变化区间为(1900～2300),这是因为随着a值的变化,生产量和产品的价格都降低了,因此厂商的利润下降的趋势就更快了。

总的来说,a值和产品价格、厂商周期内的生产量、市场需求以及厂商的利润都成反比,因此,厂商应当加大低碳力度的研究,从而使自己生产的产品更具竞争力,占据更多的市场,从而达到提高利润的目的。

4 结语

本研究在需求的确定上除了价格的影响外,考虑了产品碳排放量的影响并研究单个厂商的生产和定价决策问题。首先,整理和分析了以往消费者偏好下的供应链研究,并以此为基础,提出研究假设条件和问题。然后,分析单个厂商的成本构成,收益构成。由于目前我国并未制定碳税政策,研究采用碳排放限额交易的约束机制,构造碳约束下基于消费者偏好的库存利润模型,通过构建Hessian矩阵对构建的模型求解,得到利润最优时的产品价格和生产量。最后,给建立的模型带入数值,进行数值分析。消费者对产品的碳排放量敏感系数跟产品价格、厂商周期内的生产量、市场需求以及厂商的利润的关系,并且解释出现这种关系的原因,提出应对措施。