施工场景下灰色小波神经网络短时交通量预测模型研究

孙 瑶 李挥剑 钱 哨

(交通运输部管理干部学院 北京 101601)

0 引言

关于短时交通量预测,已有学者针对不同场景开展了较为详尽的研究与分析,研究场景涉及主干道、矿区道路、高速公路、立交转向等。赵磊娜等[1]研究了主干道路的短时交通量预测模型,基于时变滤波经验模态分解和最小二乘支持向量机构建了组合模型,组合模型的预测精度有所提升。王延明等[2]基于弹性系数法和矿区建设规划对工业矿区专用公路交通量预测展开研究。齐远[3]将BP神经网络运用至高速公路场景交通量预测中。连萌等[4]针对高度城市化地区的高速公路交通量预测精度不足问题,挖掘交通量预测误差因素,提出基于手机信令数据的预测方式,提升预测精准度。王晓阳等[5]将降雨因素考虑作为影响交通量特征因素,建立R—DBN、R—LSTM预测模型,通过对比分析常规深度学习模型,发现提出的预测模型预测精度更高,提升了预测模型的推广以及泛化能力。孙朝云等[6]基于高速公路服务区场景开展交通量预测研究。他们提出了一种基于改进粒子群算法和XGBoost融合改进的高速公路服务区交通量预测模型,匹配了高速公路服务区交通量实际调查数据与交通量之间的预测模型映射关系,能够持续迭代优化参数,收敛速度更快,精准预测不同类型交通参与要素的交通量数据。贾兵兵等[7]针对高速公路立交转向场景,运用BP神经网络进行交通量预测,并反复迭代了交通量增长系数。李双宝等[8]针对机场集疏交通流预测方法开展研究,利用重力模型和二元Logit模型进行预测模型的构建,从而有效地提升了机场集疏交通量的预测精度。张伟斌等[9]建立了微观层次的交通因子状态网络模型,用以实现城市交叉口场景的交通流预测,该预测模型相较于传统模型预测误差下降了7.62%。雷定猷等[10]针对高速公路场景,提出了一种基于非线性主成分分析和GA—RBF神经网络的交通量预测方法,该方法可降低不同指标之间的相关性,提升预测精度。

综上可观察到,当前对城市道路施工场景下短时交通量预测研究比较鲜见,对应的预测方法和预测模型的确定也少有研究。随着城市车辆保有率不断提升,道路扩容修缮极为常见,施工场景下短时交通量精准预测对城市交通管理效能提升具有重要意义。城市道路施工开展多呈现为非周期性,位置分散,导致交通量历史样本缺乏,很难支撑大样本量训练模型。针对城市道路施工场景下交通量的特点,构建基于灰色小波神经网络的短时交通量预测模型,将灰色预测模型小样本预测优势和小波神经网络非线性预测优势进行有效的融合,这对城市道路施工场景下短时交通量预测精准度提升具有实际意义。

1 短时交通量预测模型构建

1.1 基本思想

组合模型的基本思想是将两个及两个以上的模型进行组合,融合各模型的优势,从而有效提升结果的精确度。基于灰色预测模型适用于历史样本数据量少的研究场景的特点和小波神经网络对非线性数据的拟合效果优良的特点,构建了灰色小波神经网络模型。组合模型主要有三种方式,包括串联式、并联式和嵌入式[11],采用灰色预测模型和小波神经网络模型串联组合的形式,将城市道路施工场景下灰色预测模型的短时交通量预测值与观测值的残差作为小波神经网络的输入值,小波神经网络经过不断地学习和运算,得到修正后残差值,然后与灰色预测模型的短时交通量预测结果进行运算,最终计算得到灰色小波神经网络短时交通量的预测结果。

1.2 理论基础

1.2.1 灰色理论

灰色理论根据时间序列数据建立时序微分方程[12],将离散数据序列转变为规律序列,进而建立灰色时间序列的微分方程,对微分方程进行计算,可以得到预测结果,计算步骤如下:

第一步:设原始序列为:

x(0)={x(0)(k)|k=1,2,…,n}={x(0)(1),x(0)(2),…,x(0)(n)}

(1)

第二步:对公式(1)进行累加,得到累加序列为:

x(1)={x(1)(1),x(1)(2),…,x(1)(n)}

(2)

第三步:建立一阶线性白化微分方程:

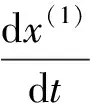
(3)

(3)式中:α为发展灰数;μ为内生控制灰数。

第四步:令原始序列组成向量Yn,那么:

(4)

(5)

第六步:求解发展灰数α

α=(BTB)-1BTYn

(6)

第七步:求解一阶线性白化微分方程,可得

(7)

第八步:通过累减算法得到预测数据序列,即可得到预测值x(0)(n):

(8)

1.2.2 小波神经网络模型

小波神经网络的优势是对非线性数据拟合效果优良[13],其原理是基于BP神经网络的架构,用小波函数代替BP神经网络的传递函数,架构如图1所示。

图1 小波神经网络架构图

小波神经网络模型的运行流程步骤如下:

(1)构建输入层、隐含层和输出层三层的小波神经网络。

(2)随机初始化小波函数的伸缩因子aj,平移因子bj,连接权重ωij(输入层与隐含层)和ωjk(隐含层与输出层)。设置小波神经网络的学习速率η1和η2[14]。

(3)将训练样本输入网络,进而计算得到短时交通量预测值。

(4)计算网络的预测输出和期望输出之间的误差e。

(5)为了使得误差满足要求,采用梯度下降法[15]修正小波神经网络的权值和参数。

(6)当训练次数>1000或e满足预测精度要求时,结束训练返回短时交通量预测结果,否则继续进行学习并训练。

1.3 灰色小波神经网络模型

灰色小波神经网络模型的运行流程步骤如下:

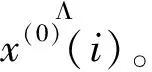
(3)训练网络。基于上一步计算所得的残差序列对神经网络进行训练。

(4)修正残差。基于上一步神经网络的输出结果对残差序列e(i)进行修正,得到修正后的残差序列e1(i)。

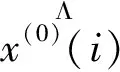
2 实例分析

研究对象为行宫西大街,选取方位为由西向东,研究时段为17:00—19:00,分析时间间隔为5min,基于连续15日17:00—19:00的数据预测第16日17:00—19:00的短时交通量数据。文章采用现场交通量计数的数据调研方式获取交通量数据,保证研究数据的准确性。利用Matlab分别基于小波神经网络模型、灰色小波神经网络模型进行城市道路施工场景下短时交通量预测的实验,第16日17:00—19:00实际值与两种模型预测值如表1所示。

表1 行宫西大街由西向东交通量实际值与预测值对比

交通量实际值、小波神经网络模型预测值、灰色小波神经网络预测值的折线图如图2所示。从图中可以看出,小波神经网络可以较为准确地预测出交通量的走向,但是波动较大;灰色小波神经网络不仅可以较为准确地预测出交通量的走向,波动情况预测也相对准确。通过图像进行初步判定后,分别计算小波神经网络和灰色小波神经网络的平均绝对误差、平均相对误差、均方误差,计算结果如表2所示[16-17]。

表2 灰色小波神经网络模型和小波神经网络模型预测效果对比

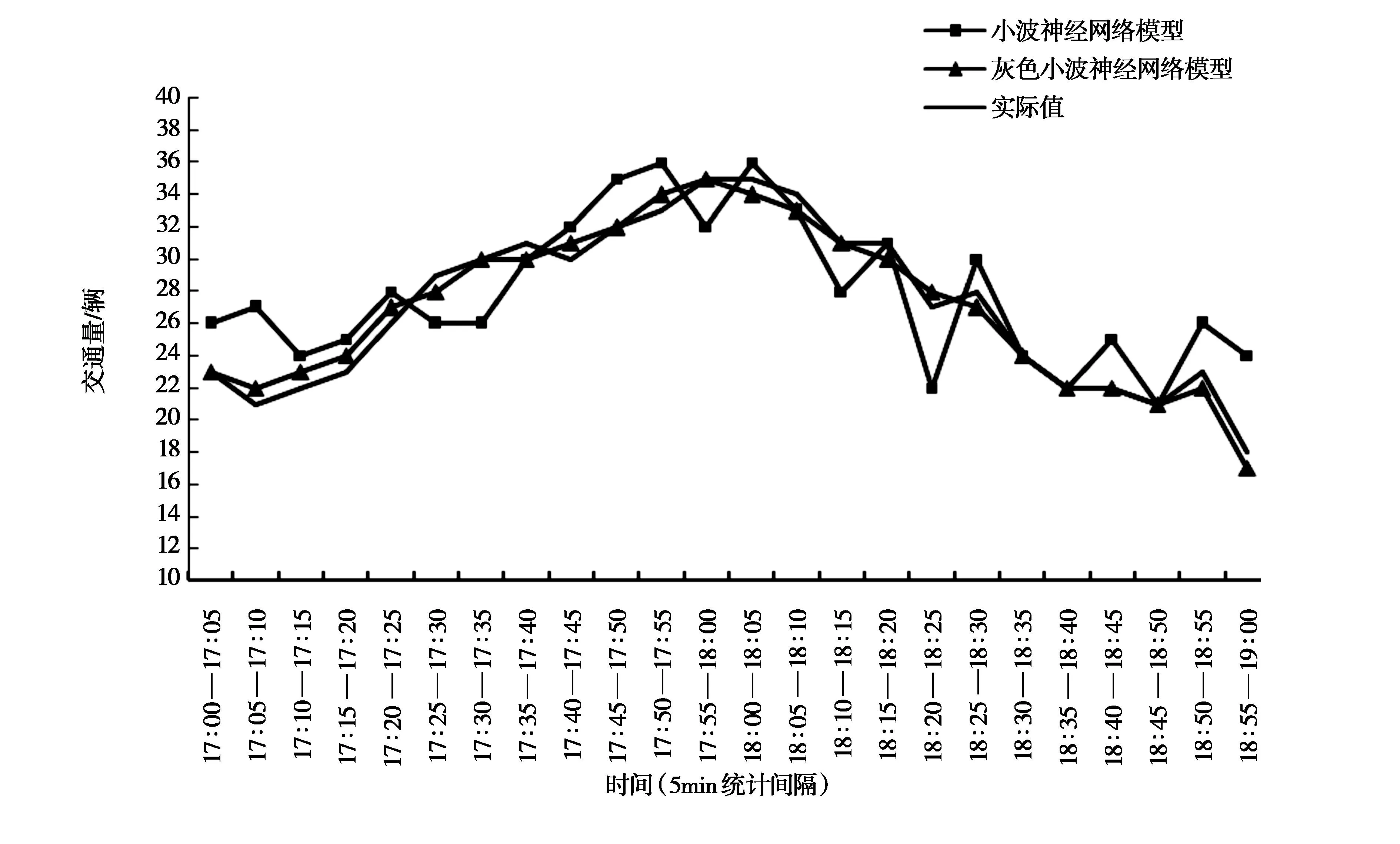
图2 短时交通量预测值与实际值曲线对比图

从表2可知,两种预测模型的平均绝对误差值、平均相对误差值和均方误差值差异显著,灰色小波神经网络预测结果的平均绝对误差、平均相对误差和均方误差相较于小波神经网络预测模型,分别降低了74.14%、75.21%和92.70%。由此可知,灰色小波神经网络预测模型精度更高。

3 研究结论

针对城市道路施工场景下短时交通量的预测进行了研究,构建了灰色小波神经网络模型。其中,灰色预测模型适用于样本数据有限的预测工作,而小波神经网络预测模型适用于具备非线性样本数据的预测工作。提出的灰色小波神经网络短时交通量预测模型创新性地将灰色预测模型和小波神经网络预测模型特点有效结合,适合历史样本数据量少且具备非线性数据特点的城市施工道路应用场景。研究结果表明,灰色小波神经网络短时交通量预测模型的平均绝对误差、平均相对误差和均方误差相较于小波神经网络短时交通量预测模型,分别降低了74.14%、75.21%和92.70%,预测精度显著提升,且能够较为准确地预测短时交通量的走向和波动情况,更加适用于城市道路施工场景的短时交通量预测。但在灰色小波神经网络短时交通量预测模型中尚未考虑预测时间间隔对预测结果的影响,有待进一步深入探索和研究。