电动辅助转向电机控制研究及EMC设计

李 任,刘卫平,卢希全,杨祥卓,张希明,刘雪明,赵 塔

(1.吉林大学 仪器科学与电气工程学院,长春 130061; 2.中车长春轨道客车股份有限公司,国家轨道客车工程研究中心基础研发部,长春 130113)

0 引 言

转向系统是商务车在行驶过程中,为转动方向以及平稳运行提供的助力控制系统。传统的液压助力转向系统电机采用的是体积大、效率低的异步电机,由于存在液压油泄露以及低温预热等问题,导致转向系统整体表现不佳。使用电动助力转向系统,相比于液压动力转向,不仅提高了安全性,而且油耗低,便于操作,因此被很多汽车生产厂家采用。

永磁同步电机因内部结构简单、占用空间小、重量轻、能量转换效率高、造价成本低等优点而被广泛应用于航空航天、无人机和电动汽车等领域[1]。衡量伺服系统整体性能关键是系统是否具有稳定性以及较强的抗干扰能力,因此采用合适的控制策略及其重要。传统的永磁电机是用霍尔传感器检测转子位置,为降低制造成本,减少系统的体积,笔者采用永磁同步电机系统以及无位置传感器的控制策略。应用模糊PID算法对永磁同步电机控制,使用扩展卡尔曼滤波器作为观测器对永磁同步电机转子进行跟踪[2]。

1 构建永磁同步电机数学模型

在永磁同步电机矢量控制中,有三相A-B-C坐标系、两相静止α-β坐标系、以及空间旋转坐标系[3]。三相A-B-C坐标系通过Clark变换成两相静止α-β坐标系如下:

(1)

两相静止α-β坐标系通过Park变换变成空间旋转坐标系如下:

(2)

同理也可以由两相静止α-β坐标系逆变换成三相A-B-C坐标系,称为Clark逆变换。可以由空间旋转坐标系通过Park变换变成两相静止α-β坐标系,成为Park逆变换[4]。Park变换以及Park逆变换需要转子的旋转的电角度。

永磁同步电机的数学模型由电压、磁链、电磁转矩、机械运动和转矩方程组成。

电压方程为

(3)

磁链方程为

(4)

电磁转矩方程为

(5)

机械运动方程为

(6)

等效转矩方程为

(7)

其中ud、uq是由定子三相电压经过坐标变换成的d-q轴分量;id、iq是由定子三相电流经过坐标变换成的d-q轴分量;Ld、Lq是定子绕组d-q轴电感;ψd、ψq是定子磁链d-q轴分量;R是定子上的等效电阻;Te、TL分别是电机输出转矩和负载转矩;p是转子极对数;J是转动惯量;ωe是转子电角度的速度[5]。

2 永磁同步电机矢量控制方法

永磁同步电机的矢量控制方法是一种常用的控制方法,其基本结构如图1所示。永磁同步电机由速度环以及电流环两个闭环控制,通过拓展卡尔曼滤波器得到永磁同步电机的电角度的估计值[6]。应用拓展卡尔曼滤波器可取代传统位置传感器,既降低了成本又减小了整套系统的体积,把拓展卡尔曼滤波器估计出的电角度应用于Park变换以及逆变换中。q轴的电流输入由设定的固定值与实际值相减得到[7]。d轴的电流为励磁电流,用于产生电磁场,将电流控制成id=0。q轴为转矩电流,用于负责产生转矩,使转子在电磁场的作用下旋转并拖动负载,q轴的目标电流来源于速度环的输出。得到的电流差经过内环的PI(Proportional Integral)调节器再通过Park变换进入SVPWM(Space Vector Pulse Width Modulation)调制,产生能控制电机的信号,PI调节器中采用模糊PID(Proportional Integral Derivative)算法。

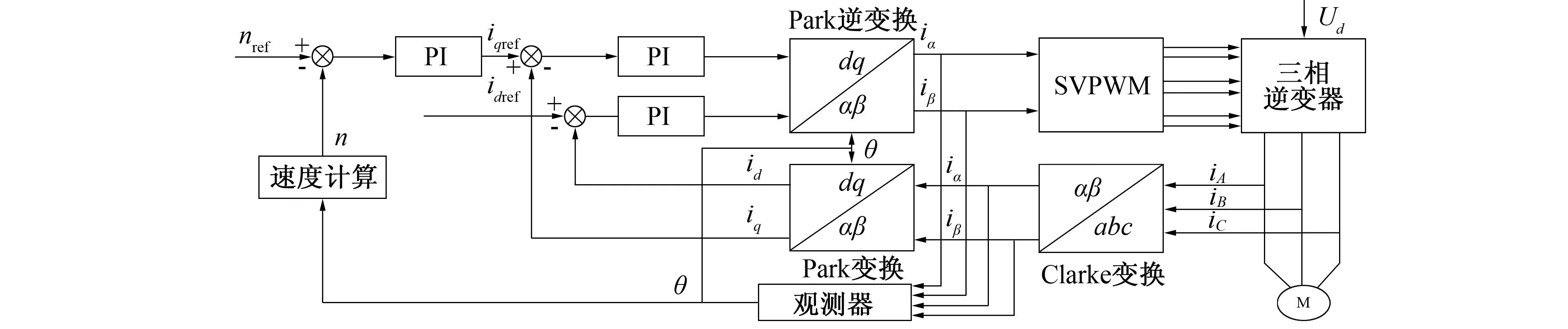
图1 永磁同步电机的矢量控制基本结构图

3 模糊PID控制

3.1 模糊控制系

模糊控制系统如图2所示,在整个系统中,模糊控制器为核心部分,其中包含模糊化、模糊推理以及逆模糊化。规则库保存被控对象的控制规则,模糊化是将某个物理量模糊性表述,模糊推理是根据规则库里的模糊规则进行推理,其推理出的结论仍为模糊的,需要逆模糊化,使推理出的结果转换成明确的结果[8]。

图2 模糊控制系统

3.2 模糊自适应PID控制

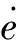
3.3 模糊规则的设定

模糊规则的设定是由专家经不断实践以及经验得到,模糊PID控制器性能高低决定永磁同步电机控制的精度,其主要由有效的模糊控制规则决定,表1～表3给出了PID控制器的模糊规则。

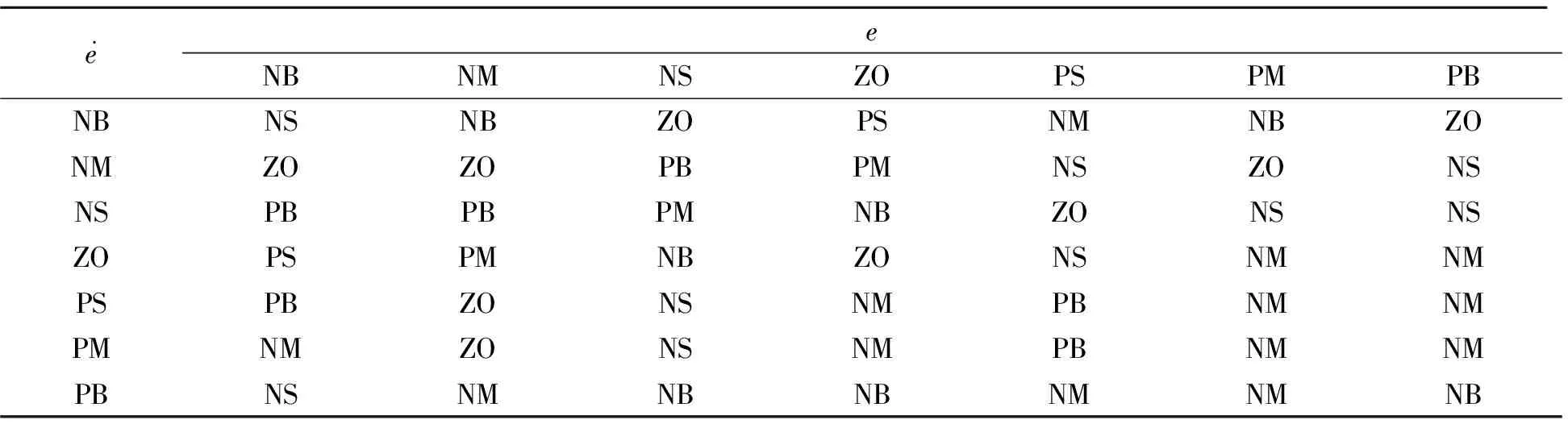
表1 Kp模糊规则

表2 Ki模糊规则

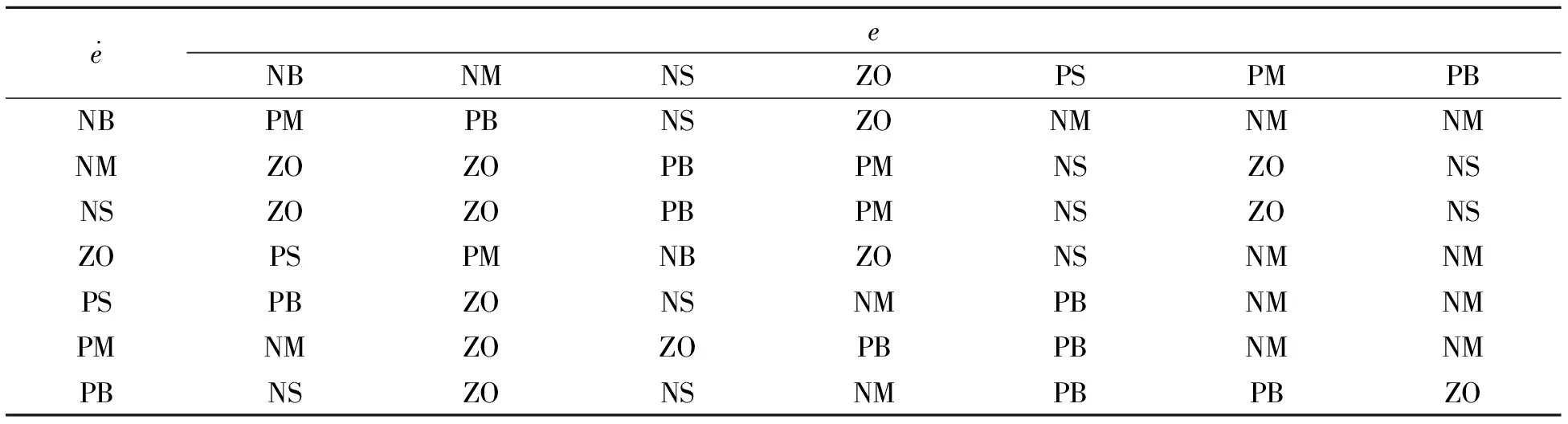
表3 Kd模糊规则

查询模糊PID规则表,并进行相应的逆模糊化可得到Kp、Ki、Kd参数。

3.4 模糊PID控制仿真

笔者应用可信度高的软件工具Matlab,并在其Matlab中使用simulink分别建立模糊PID控制系统以及常规PID控制系统,这样能对比出差异,显示模糊PID控制的优势[10]。在建立模糊PID控制模块时,需要模糊推理机指定相应的规则,其是依据专家实验人员经过实验得出,图3为2种PID控制方法的simulink仿真模型,图4为常规PID控制仿真波形图,图5为模糊PID控制的仿真波形图。

图4 常规PID控制仿真波形图

通过图4,图5对比可看出,模糊PID控制精准度更高,且反应时间更快,模糊PID在系统仿真时间为0.6 s时达到稳定,且稳定后做小幅度摆动; 传统PID控制在9.5 s时达到稳定,反应时间极慢[11]。最后将模糊PID控制系统整合到永磁同步电机控制系统中,使永磁同步电机控制中的PI控制采用模糊PID控制算法。

4 扩展卡尔曼滤波器

4.1 扩展卡尔曼滤波器基本原理

扩展卡尔曼滤波器是基于卡尔曼滤波器衍生的一种状态估计方法,卡尔曼滤波器常常应用于线性系统,而扩展卡尔曼滤波器可应用于非线性系统[12]。扩展卡尔曼滤波器在控制策略上更加完善,可抑制随机干扰,其是基于卡尔曼滤波器改进的,对非线性系统进行最优估计。

对非线性系统线性化后,扩展卡尔曼滤波器方程为

1) 状态预测:

(8)

2) 预测协方差矩阵:

P(k|k-1)=φ(k|k-1)P(k-1|k-1)φT(k|k-1)+Q。

(9)

3) 状态更新:

(10)

4) 卡尔曼增益矩阵:

Kg(K)=P(K|K-1)HT/(HP(k|k-1)HT+R)。

(11)

5) 协方差矩阵更新:

P(k|k)=(1-Kg(k)H)P(k|k-1)。

(12)

4.2 扩展卡尔曼滤波器在永磁同步电机中的数学建模

由式(1)～式(7),假设永磁同步电机的状态变量x=[id,iq,θ,ωe]T,输入量u=[ud,uq]T,输出量y=[id,iq]T,永磁同步电机的状态方程为

(13)

(14)

在方程中f(x)为

(15)

基于以上永磁同步电机的数学模型进行离散化[13]:

x(k+1)=f[x(k)+B(k)u(k)+W(k)],

(16)

y(x)=C(k)x(k)+V(k)。

(17)

由式(17)得出,拓展卡尔曼滤波是以电压为输入量,以q轴d轴上的电流为输出量,状态变量为q轴d轴上的电流,以及电角度和电角度的速度[14]。图6为拓展卡尔曼滤波器在永磁同步电机上的控制框图,该系统可由电流电压传感器检测出三相电流以及电压,三相电流经过Clark变换后可得到iα、iβ的电流。电压经Clark坐标变换成uα、uβ的电流,由输入及输出量输入到卡尔曼滤波器可估计出电角度以及角速度[15]。

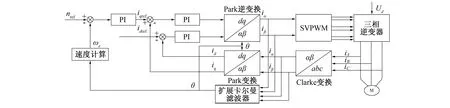
图6 拓展卡尔曼滤波器在永磁同步电机上的控制框图

4.3 基于卡尔曼滤波系统的永磁同步电机控制仿真

图7为基于拓展卡尔曼滤波器的永磁同步电机矢量控制的仿真模型。

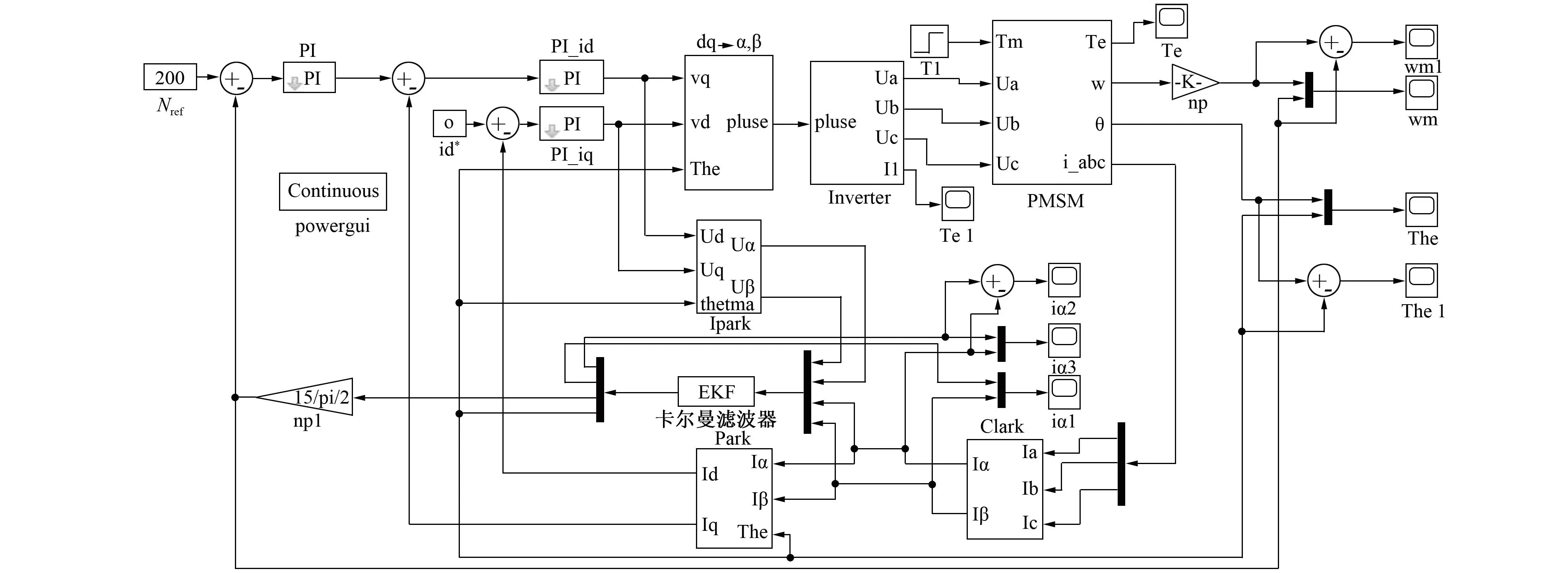
图7 拓展卡尔曼滤波器的永磁同步电机矢量控制仿真模型

通过扩展卡尔曼滤波器,可在无位置传感器的情况下,估算出永磁同步电机转子的位置[16]。图8、图9分别是电机转速的无感估算值与有感计算值。通过仿真结果可得出,在给定参考转速为125 r/s,仿真结果与实际的转速基本一致,可应用于商用车电动辅助转向电机控制。

图8 125 r/s转速估计值

5 电机驱动系统EMC设计

5.1 EMI分析方法

电机驱动系统中的EMI分析法是通过仿真和实际测试进行的,并应用多导体传输线理论建立输出非屏蔽线路的高频电路模型以及逆变器输入模型。采用谐振单元方法建立高频等效模型,同时利用等效电路模型中电容、电阻以及电感参数的计算方法,以电机驱动为对象,完成高频等效电路模型。建立电机驱动其他部件的电路模型以及电机驱动系统电磁干扰源,搭建测试平台,测试干扰电流波形,与仿真结果进行对比并进行验证。

5.2 电机驱动EMC设计

电机驱动中的EMI主要有共模和差模干扰,其中需要解决的是共模干扰。电机驱动EMC设计是抑制电机驱动系统传导时干扰源发射强度以及切断传导EMI传播路径。抑制干扰发射源发射强度从控制策略的角度进行抑制,抑制IGBT(Insulate-Gate Bipolar Transistor)等元件的电压电流变化率。还可以通过改变电路结构减少EMI干扰。采用有源EMI滤波技术切断传导EMI传播路径,其基本原理是将检测到的EMI电流或电压方向回馈给系统,以抵消系统中传导EMI的电压或电流。此外,还可以采用屏蔽式的方法抑制EMI。

6 结 语

笔者提出一种基于模糊PID以及拓展卡尔曼滤波器的商用车电动辅助转向电机控制方法,该控制策略是在永磁同步电机的数学模型基础上搭建的,使用模糊PID算法比常规PID算法更加精准,反应速度更快。拓展卡尔曼滤波器可取代传统的传感器,能减小控制器的体积及成本。由实验结果可看出,使用拓展卡尔曼滤波器可精确地估算出转子的位置,从而取代传统传感器,该控制策略可以应用于商用车电动辅助转向电机控制。最后,针对电机驱动系统进行了相应的EMC设计,为完整的电机EMC研究提供了思路。