改进人工蜂群算法及其在工程设计中的应用
2023-12-26宋婧媛张邦成
李 波,宋婧媛,张邦成
(长春工程学院 a.计算机技术与工程学院; b.吉林应急管理学院; c.机电工程学院,长春 130012)
0 引 言
工程设计问题通常需要在一组严格的规范约束下和在相互冲突的优化目标(例如:项目的成本和产品的稳健性,或产品的重量和产品的尺寸)之间做出妥协。因此工程中的设计问题可以被建模为受约束的多目标优化问题(CMOP:Constraint Multi-Objective Problem)[1]。
虽然工程设计问题与一般的CMOP具有相同的数学形式,但在实际应用中,工程设计问题的目标函数和约束通常具有较高的计算代价,即目标函数的计算过程需要消耗较多的时间和计算资源。由于很多工程设计问题的目标函数是不连续的,并且有些问题的目标函数缺少先验知识,难以通过仿真对其进行建模,往往只能把目标函数作为黑盒进行优化,这极大地增加了优化问题的难度。因此,需要设计准确且高效的优化算法对问题进行优化。
近年来,群智能优化算法在智能优化领域取得了很大突破,对多目标优化和受约束的优化问题都具有较好的求解性能[2]。群智能优化算法包括蚁群算法(ACO:Ant Colony Optimization)、粒子群优化算法(PSO:Particle Swarm Optimization)、ABC(Artificial Bee Colony)算法等。其中AOC算法是受自然界中蚂蚁搜索食物行为的启发,其基于对自然界真实蚁群的集体觅食行为的研究,模拟真实的蚁群协作过程,在求解性能上具有很强的鲁棒性和搜索较好解的能力。但AOC算法计算量大,求解所需的时间长,收敛速度慢,易陷入局部最优[3]。PSO算法具有相当快的逼近最优解的速度,可有效地对系统的参数进行优化,其优势在于求解一些连续函数的优化问题。但PSO算法容易产生早熟收敛、局部寻优能力较差等问题[4]。ABC算法自提出便受到研究者的广泛关注,目前ABC算法及其变种算法已被应用于单目标、多目标以及有约束优化问题的求解,且已在不同的应用领域中证明了其有效性。因为ABC具有多样的搜索策略,能在优化过程中根据算法的历史搜索情况灵活地对算法的搜索策略进行调整,所以ABC具有较高的求解精度,且算法的稳定性和健壮性较高,特别适用于较为复杂的优化问题[5]。
ABC算法源于对蜂群内部分工机制及其觅食行为的模拟。产生智能行为的蜂群觅食模型主要由食物源、受雇佣的觅食者、非受雇佣的觅食者以及针对食物源的招募行为、放弃食物源的行为构成。该算法也被用于求解各种多目标优化问题,但ABC算法在处理这类问题时存在收敛速度慢、种群盲目搜索以及算法开发能力有限等不足[6]。在多目标优化中,优化目标之间往往存在一定的联系。在实际应用中优化目标之间通常是互相冲突的,在对一个优化目标进行优化时,解在其他目标上的质量往往会下降,即多目标优化问题(MOP:Multi-Objective Problem)中的优化目标很难被同时优化[7]。在使用ABC算法求解MOP问题时,往往无法找出一个MOP的最优解。
因此,笔者在ABC算法基础上引入了群智能优化和进化优化中常见的交叉、变异算子,结合算法的基本原理提出了一种基于支配和分解的多目标ABC算法,称为MOABC/DD(Multi-Objective Artificial Bee Colony based on Dominance and Decomposition)。MOABC/DD借鉴了群智能优化和进化优化中常见的交叉、变异算子,通过交叉和变异算子两个步骤后生成一个新候选解。为保证候选解的多样性,设计了一种基于分解的多目标优化策略,该策略采用在目标空间中均匀分布的一组权重向量,将MOP分解为若干个标量子问题。同时每个权重向量取与其距离最近的T个权重向量作为其邻居(neighbor)。在基于分解的搜索过程中,每个权重向量对应一个子问题,每个子问题会选择自己的最优解[8]。因此算法设计了基于邻居的交叉和变异策略,从而使其有针对性地进行搜索,提高了可行解的质量[6]。
1 相关知识
ABC算法包含3个搜索阶段,即3种不同类型的搜索策略,分别为雇佣蜂、观察蜂和侦察蜂搜索[9]。算法模拟蜂群寻找蜜源并采蜜的过程将蜜蜂分为不同的工种,所有工种共同的目标为找到优质蜜源。在ABC算法中,不同搜索策略的目标均为搜索到优质解,将候选解(对应蜜源)称为食物源。
为更好地理解超多目标优化问题及Pareto支配的思想,需要明确以下概念。
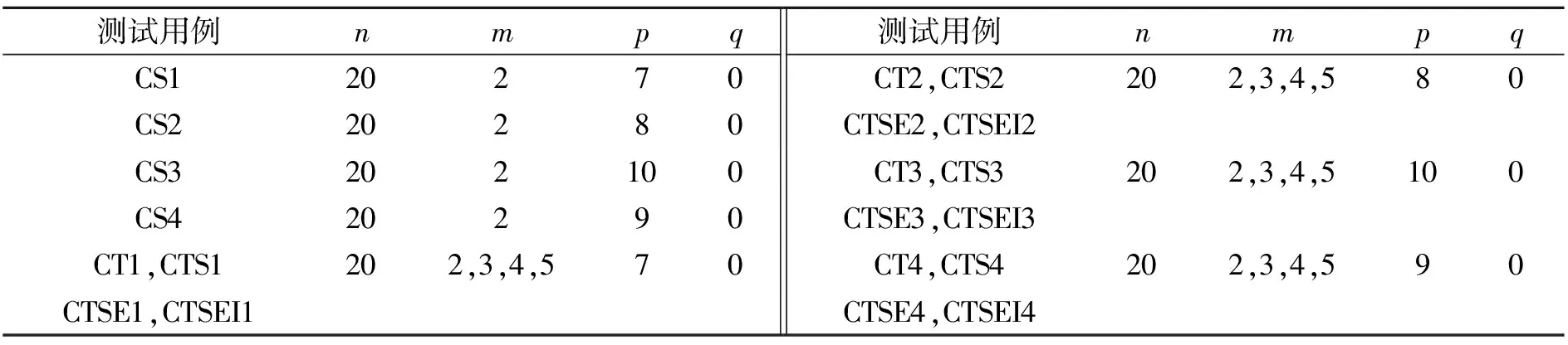
定义1(帕累托支配关系(Pareto dominance relationship)) 当且仅当∀ft(xi)≤ft(xj),且∃ft(xi) 定义2(非支配个体(non-dominated individual)) 个体xi是种群中的非支配个体,当且仅当不存在任何个体xj,满足xj支配xi。 定义3(Pareto最优解集(PS:Pareto Set)) 超多目标优化算法中,不被任何候选解所支配的个体称为非支配解,它们所构成的集合称为Pareto最优解集。 定义4(Pareto前沿(PF:Pareto Front)) Pareto前沿是由理论上优化问题的最优解集合拟合而成的目标空间中的一个超平面。在实验研究中,通常使用已知的非支配解的集合代表问题的Pareto前沿。 图1对已有的多目标优化策略进行了分类,并给出了典型算法名称。已有的多目标优化算法根据其优化策略可分为基于分解、支配和指标的3种多目标优化算法[10]。其中基于分解和支配的多目标优化策略是多目标优化当中常见的2种优化策略。 图1 已有多目标优化算法分类 基于分解的多目标优化策略将MOP分解为能覆盖目标空间的多个单目标子问题,并对子问题进行并行且独立的求解; 算法用所有子问题的最优解对PF进行拟合。通常,基于分解的优化策略利用一组指向目标空间不同方向且分布均匀的向量对问题进行分解,这组向量通常被称作权重向量(weight vector)或参考向量(reference vector)。这些向量将目标空间分解为若干个子区域。算法可以令每个权重向量对应一个标量子问题,这样MOP就被分解为了若干个单目标问题。每个子问题的最优解都可以用于表示PF的一部分。算法用所有子问题的最优解构成PS,对问题的PF进行拟合。由于权重向量的分布是均匀的,所以这类算法能较好地拟合PF的形状。采用基于分解的求解策略时,算法只需计算各个候选解在每个子问题上的适应度,时间开销能得到较好控制,因此基于分解的基于指标的多目标进化算法(MaOEA)具有较高的优化效率。 基于支配的多目标优化的基本思路为利用帕累托支配规则对候选解进行选择,从而选取优质解启发算法的后续优化。最常见的基于支配的选择方法为,首先选取候选解中的非支配解,再选择剩余候选解中的较优解,直至选取到足够的候选解为止。基于支配的算法通过借助帕累托规则能妥善处理进行多目标优化时面临的失去选择压力的问题。采用基于支配的思路处理多目标优化问题时需要注意的是,有时会出现选择的解不足以填充种群或其数量超出种群规模的问题。在这种情况下,很多基于支配的多目标优化策略针对算法演进过程中丧失选择压力的问题引入了额外的候选解评价机制,使算法在种群的每一子代都能选取高质量的个体构成新的种群[11]。 笔者提出了一种改进的多目标ABC算法(MOABC/DD),用于求解CMOP。该算法结合了多目标优化中常见的基于分解的多目标优化策略和基于支配的多目标优化策略,从而在促进算法收敛和维持解的多样性之间达到平衡,使算法在具有较高的求解效率的同时能产生对问题的PF拟合效果较好的非支配解集。 算法1描述了MOABC/DD的算法框架,算法在初始化阶段,随机初始化N个随机食物源,同时初始化一组权重向量λ={λ1,λ2,…,λN},并根据各优化目标对应的目标函数对食物源进行评价。算法交替执行雇佣蜂搜索和观察蜂搜索,并根据特定条件执行侦察蜂搜索,通过重复执行不同类型的搜索行为,不断提高解的质量[12]。最终在算法达到终止条件时,终止执行搜索并输出其搜索到的非支配可行解。MOABC/DD算法提出了基于分解的雇佣蜂、基于支配的观察蜂和基于优化进程的侦察蜂3种搜索策略[13]。通过3种不同类型的搜索策略,MOABC/DD兼顾算法的收敛性能和解的多样性,并保证得到CMOP的可行解。 算法1 MOABC/DD算法框架。 输入:搜索空间Ω; 输出:非支配解; 1) 初始化N为随机食物源; 2) 初始化权重向量λ={λ1,λ2,…,λN}; 3) 根据权向量λ生成子问题; 4) 评价食物来源的客观价值; 5) While终止条件不满足do: 6) 执行蜂蜜搜索; 7) 执行旁观者蜂搜索; 8) for每个子问题do: 9) if如果没有更新k次迭代then: 10) 执行侦察蜂搜索行为; 11) end 12) end 13) 更新NA; 14) end 15) 输出非支配可行解。 ABC的基本思想为通过模拟蜜蜂采蜜的行为对搜索空间进行搜索。蜜蜂的搜索即产生新候选解的过程。ABC需要算法不断生成新候选解,通过将新生成的候选解与旧候选解进行比较淘汰劣质候选解,从而促进算法向候选解的质量提高的方向收敛,最终搜索到问题的最优解或近似最优解[14]。MOABC/DD借鉴了群智能优化和进化优化中常见的交叉、变异算子,通过交叉和变异算子两个步骤后生成一个新候选解。为保证候选解的多样性,笔者设计了一种基于分解的多目标优化策略,该策略采用在目标空间中均匀分布的一组权重向量,将MOP分解为若干个标量子问题。同时每个权重向量取与其距离最近的T个权重向量作为其邻居(neighbor)。在基于分解的搜索过程中,每个权重向量对应一个子问题,每个子问题会选择自己的最优解[15]。因此算法设计了基于邻居的交叉和变异策略。其中变异算子为 ui=xr1+F(xr2-xr3), (1) 其中ui为第i个权重向量对应的交叉算子产出解,xr1、xr2、xr3分别为从第i个权重向量和其邻居权重向量对应的子问题最优解中随机选择出的3个个体,F为交叉因子,用于控制交叉算子产生的新解的个体在搜索空间中可能存在的范围。 在通过变异算子得到ui后,算法进一步通过变异算子对其进行修改,并得到一个新的候选解vi。该变异算子为 (2) 其中vi,j为新候选解vi的第j个维度,rand(0,1)为产生0~1之间随机实数的随机数函数,但服从均匀分布,cr为交叉概率,xi,j为第i个权重向量对应的原最优解xi的第j个维度。 算法2描述了MOABC/DD中基于分解的雇佣蜂搜索策略。雇佣蜂搜索阶段通过进行基于分解的多目标优化能保证解在目标空间中的分布较为均匀,即具有较好的解的多样性[16]。维持解的多样性对多目标优化十分关键,因为多样性对后续的搜索以及最终得到的解对PF的拟合程度具有重要的影响。 雇佣蜂策略采用惩罚边界交叉(PBI:Penalty-Based Boundary Intersection)分解策略设计各子问题。因此子问题的数量与权重向量的数量相等。对第i个权重向量,对应的子问题为 minimizegpbi(x|λi,z*)=d1+θd2, subject tox∈Ω, (3) 其中 (4) d2=‖F(x)-(z*-d1λi)‖, (5) 由于各子问题通过式(3)转化为标量化的函数,所以在算法进行解的评价和选择时,各子问题可拥有唯一的最优解。基于分解的策略简化了多目标优化的评价和选择过程,对提高算法效率具有重要意义。 雇佣蜂搜索策略起始时计算权重向量之间的几何距离,每个权重向量选择与其欧氏距离最近的T个权重向量作为其邻居[17]。然后算法根据权重向量构建N个子问题,并从食物源中为每个子问题选择最优解。之后,对每个食物源,算法根据式(1)和式(2)执行变异算子和交叉算子,从而产生一个新候选解。随后计算新生成的候选解在各目标函数上的取值,并从已有食物源和新生成的候选解中为每个子问题选择各子问题的最优解。最后用子问题的最优解更新食物源。 算法2 基于分解的雇佣蜂搜索。 输入:N种食物来源; 权向量λ={λ1,λ2,…,λN}; 输出:N个更新的食物来源; 1) 计算权向量之间的距离; 2) for每个权重向量do: 3) 选择T个最接近的权值向量作为其邻居; 4) end 5) while终止条件不满足do: 6) for每只受雇的蜂蜜do: 7) 执行变异运算符; 8) 执行交叉运算; 9) end 10) 评估每个新解决方案的客观价值; 11) 融合食物来源和新的解决方案; 12) 根据权向量λ={λ1,λ2,…,λN}生成子问题; 13) for对每个子问题do: 14) 找到最优解; 15) end 16) 更新食物来源; 17) End 根据算法2,雇佣蜂、观察蜂和侦察蜂阶段的时间复杂度均为O(n2)。因此,MOABC/DD的时间复杂度为O(n2)。需要注意的是,在优化过程中并不总是处于执行侦察蜂阶段。同时,MOABC/DD不需要外部解集用于维护非支配解,它只维护一套食物源。因此,其空间复杂度为O(n)。 将所提算法应用于机电执行器设计问题(MODAct:Modification Actuators),该问题为一种实际的工程设计问题。机电执行器是由电动机和齿轮箱组成的系统,其作用是使其他组件在位置控制设置或动作生成过程中旋转。机电执行器被广泛应用于多种不同的应用中。由于机电执行器应用范围广,各种设计目标之间相互冲突,对问题具有严格的限制,所以机电执行器的设计问题是一种典型的工程设计CMOP。在机电执行器设计问题中应用对笔者提出的改进多目标ABC,能对该算法求解CMOP的性能进行测试和分析。 在笔者的机电执行器设计问题中,目标机电执行器由步进电机、k级齿轮(一级齿轮由一个主动小齿轮和一个从动大齿轮构成)和一个容纳各部件的容器构成。一个机电执行器可以被建模为包含k+1个组件的组件链,各组件分别包括:1) 预测组件输出速度、输出扭矩以及与组件相关约束的物理模型; 2) 代价模型ci; 3) 用于创建和组装机电执行器系统的几何模型。基于物理模型和代价模型,或通过检查几何模型,可将机电执行器设计问题的优化目标和约束表示为数学形式。 对问题建模,当计算步进电机的性能时,假设步进电机处于稳态运行的前提下,步进电机的参数θ可从现有商用两相步进电机的5种可能的参数组合中进行选择[18]。定子线圈绕组可通过缩放填充因子FF或电阻Rscale进行调整。所有步进电机都由一个啮合的圆柱形表示,其直径和高度与其实际尺寸相对应。他们的成本代价由两部分组成:组件的固定贡献和其所选绕组的可变部分。问题中齿轮被建模为符合ISO标准的钢齿轮,其特征包含齿数Zi{1,2},轮廓偏移xi{1,2),模数mi和厚度bi。齿轮的三维构成方式通过圆柱形啮合关系进行几何表示。齿轮的代价通过齿轮的体积进行估算[19]。作用于每个部件上的转速和扭矩可从电机开始依次计算。在本研究中机电执行器各组件之间的能量流被认为是完美的(即没有能量损失和完美的刚性连接)。对给定的输入条件(电源电压Um、最大电流Imax和所需的输出转速ω),可以计算输出端的扭矩T。一组由电源电压、电流、所需速度和扭矩构成的参数构成为一个工作点(operating point)。输出端与所需扭矩的偏差称为扭矩过剩[20]。齿轮的三维位置由每个齿轮级的两个决策变量指定:1) 沿轴的平移di,2) 小齿轮和从动轮之间的角度γi。使用所有啮合轮廓的组合检测组件间的碰撞并计算系统边界框的大小。最后,采用凸面形的外壳,假设壁厚固定,所需的材料成本选择被添加到总成本中。使用这种建模方法,机电执行器设计问题的目标在于找到一组在指定工作点运行的合适电机和齿轮参数,并保证其符合齿轮的机械完整性、空间配置等约束[21]。 搜索空间对应机电执行器每个组件的组合。齿轮和电机的决策变量均为整型。为了使更多的优化算法被用于机电执行器设计问题中,笔者定义的MODAct问题将整型变量与相关的连续变量组合为一个实数,其整数部分表示整型变量,小数部分则映射到其他变量。具体映射方式为: 1) 电机选择变量和填充因子FF共同组成变量mF; 2) 齿轮的齿数Zi{1,2}和其齿廓位移构成变量Zxi{1,2}。 在笔者所采纳的MODAct测试用例中,设置k=3,并设计了5种不同的目标函数,通过不同目标函数的组合,可构建不同的MODAct基准测试用例。具体优化目标设计如下。 1) 总成本最小化: (6) 2) 最大化每个考虑的工作点的最小过剩扭矩 (7) 其中ΔTj=Tj-Tdesired,j。 3) 最大化所有齿轮弯曲SF和点蚀SH的安全系数的调和平均值 (8) 4) 最大化电能到机械能的转换效率 (9) 5) 最小化转换率 (10) 基于对以上目标函数的组合,文中的MODAct问题可以分为5类:1) CS,2) CT,3) CTS,4) CTSE,5) CTSEI,各自对应上面5个参数的组合。 此外,MODAct考虑了机电执行器设计中常见的各种不同约束。这些约束可被分为4类:1) 对齿轮的约束(如足够的接触比、有限的滑动速度、无干扰、足够的弯曲和机械强度等); 2) 最小化扭矩过载工作点; 3) 边界框尺寸的上限(bby≤50 mm且bbz≤35 mm); 4) 从输出轴到所需坐标的距离限制在5 mm之内。 以上4种不同类型的约束的复杂性不同,而且存在于机电执行器设计过程中的不同阶段,例如约束1)和2)通常存在于MODAct的早期阶段; 有些约束对应特定的应用规格和需求,例如约束3)和4)对机电执行器的技术规格提出了具体要求。不同的约束可以与不同的MODAct优化目标进行组合。将以上的4种约束与5种不同的MODAct问题进行组合能得到20个基准MODAct测试用例,将这些基准测试用例使用目标名称加约束类型进行命名。例如CTS类型的MODAct问题与约束2)结合可以得到基准测试用例CTS2。 表1给出了所有的测试用例实例与目标空间约束的参数个数(n、m、p、q),其测试用例的搜索空间上下界分别为 表1 MODAct基准测试用例 x(L)=[0,0.3,9,30,0.3,5,020,-π,9,30,0.3,5,020,-π,9,30,0.3,5,020,-π], (11) x(U)=[5-10-6,2,41-10-6,81-10-6,1,15,20,π, 41-10-6,81-10-6,1,15,20,π,41-10-6,81-10-6,1,15,20,π]。 (12) 需要注意的是,除存在2种不同要求的最小扭矩过剩约束外,所有的约束都独立于优化目标。由表1可知,文中的MODAct基准测试用例均可以建模为CMOP,且优化目标的数量从2个到4个不等。随着优化目标数量的上升,问题优化的难度也随之升高,因此能对算法的求解精度和效率进行有效验证。 该实验对比了MOABC/DD和NSGA-Ⅱ、NSGA-Ⅲ、C-TAEA算法在20个机电执行器设计测试用例上的优化结果,将MOABC/DD算法和各对比算法分别独立运行31次。如上所述,机电执行器设计问题中的一部分优化目标为最小化优化问题,另一部分优化目标为最大化优化问题。为方便算法对基准测试用例进行优化,在实验前统一将所有的最大化优化目标转化为最小化优化目标,转化方法为求原优化目标的倒数。采用HV(hypervolume)指标对各算法产生的非支配解的质量进行评价。在对各算法的结果进行HV指标计算时,先对所有的优化结果进行标准化,即将各优化目标的目标值转化为0~1之间的实数,然后将HV指标计算的参考点设为r=(r1,r2,…,rm)T,满足r1=r2=…=rm=1。 31次独立重复实验中各算法的HV指标如表2所示。其中每个算法在每个测试用例上对应4个数值,4个数值之间以符号“/”作为间隔,其中第1个数值为独立重复实验HV指标的均值,第2个为HV指标的最优值,第3个为HV指标的最差值,第4个为独立重复实验所统计的HV指标的标准差。HV的均值、最优值和最差值均为越大越好,HV的标准差越小表明算法求解的稳定性越强,因此认为HV标准差应尽量小。 表2 各测试用例上实验结果的HV指标 由表2可看出,MOABC/DD在20个基准测试用例中的5个测试用例上同时取得了HV均值、最优值、最差值和标准差的最优结果; 其在18个测试用例上取得了最优的HV均值; 在12个测试用例上取得了最优的HV最优值,在16个测试用例上取得了最优的HV最差值; 在12个测试用例上取得了最优的HV标准差。实验结果表明,当CMOP约束类型和优化目标数量不同时,MOABC/DD都具有较为优异的优化性能。在大多数基准测试用例上MOABC/DD的实验结果都具有较高的精度,且在独立重复实验中,MOABC/DD的优化稳定性也较强。NSGA-Ⅱ/Ⅲ和C-TAEA在约束级别为3和4的MODAct实例上的性能不足,而其代表了常见和简单的机械设计问题。考虑到问题CS3和CS4,超过75%的NSGA-Ⅱ优化运行获得了近似的帕累托前沿,其超体积为50%或小于最著名的帕累托前沿,而C-TAEA未能找到有效的解决方案[22]。与其他算法相比,MOABC/DD具有更适用于MODAct问题的优化性能。 为比较MOABC/DD与对比算法在4个典型的机电执行器设计问题的基准测试用例上对PF的拟合情况,根据各算法在独立执行中得到的解在目标空间中的映射进行绘图,结果如图2所示。横坐标为最小化优化问题的变量,纵坐标为最大化优化问题的变量。因此,在4个测试用例中,解的位置越靠近左上角,算法产生的解对PF的拟合情况越好。由图2可见,MOABC/DD在4个测试用例上对PF的拟合效果较好,其产生的解在目标空间中的位置不仅更接近坐标系第1象限的左上方,而且解的分布也更为均匀,因此MOABC/DD产生的解对选取的4个测试用例的拟合效果是参与实验的算法中最好的。 图2 各算法对PF的拟合情况比较 笔者在ABC算法基础上引入了群智能优化和进化优化中常见的交叉、变异算子,并结合算法的基本原理提出了一种改进的MOABC/DD算法。将一种实际的机电执行器设计问题作为工程设计问题的基准测试用例对提出的MOABC/DD进行了验证。实验结果表明,所提出的MOABC/DD算法在求解机电执行器设计问题基准测试用例时,与典型算法相比,具有较好的问题求解精度。通过比较多次重复实验的实验结果可知MOABC/DD的实验结果较为稳定,证明了MOABC/DD具有较高的求解稳定性和健壮性。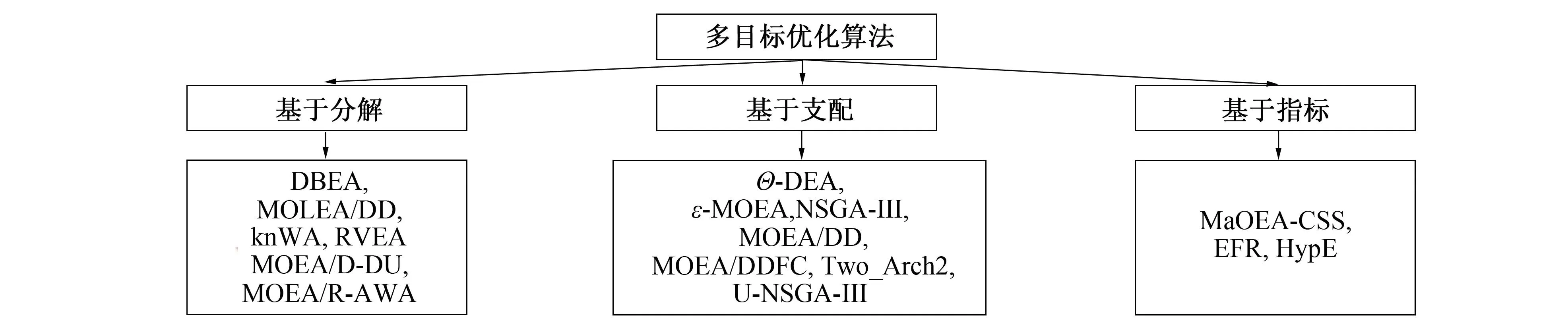
2 改进的人工蜂群算法
2.1 算法框架
2.2 新候选解生成策略
2.3 基于分解的雇佣蜂搜索策略

2.4 算法复杂度分析
3 改进的人工蜂群算法在机电执行器设计问题中的应用
3.1 问题定义
3.2 实验结果比较

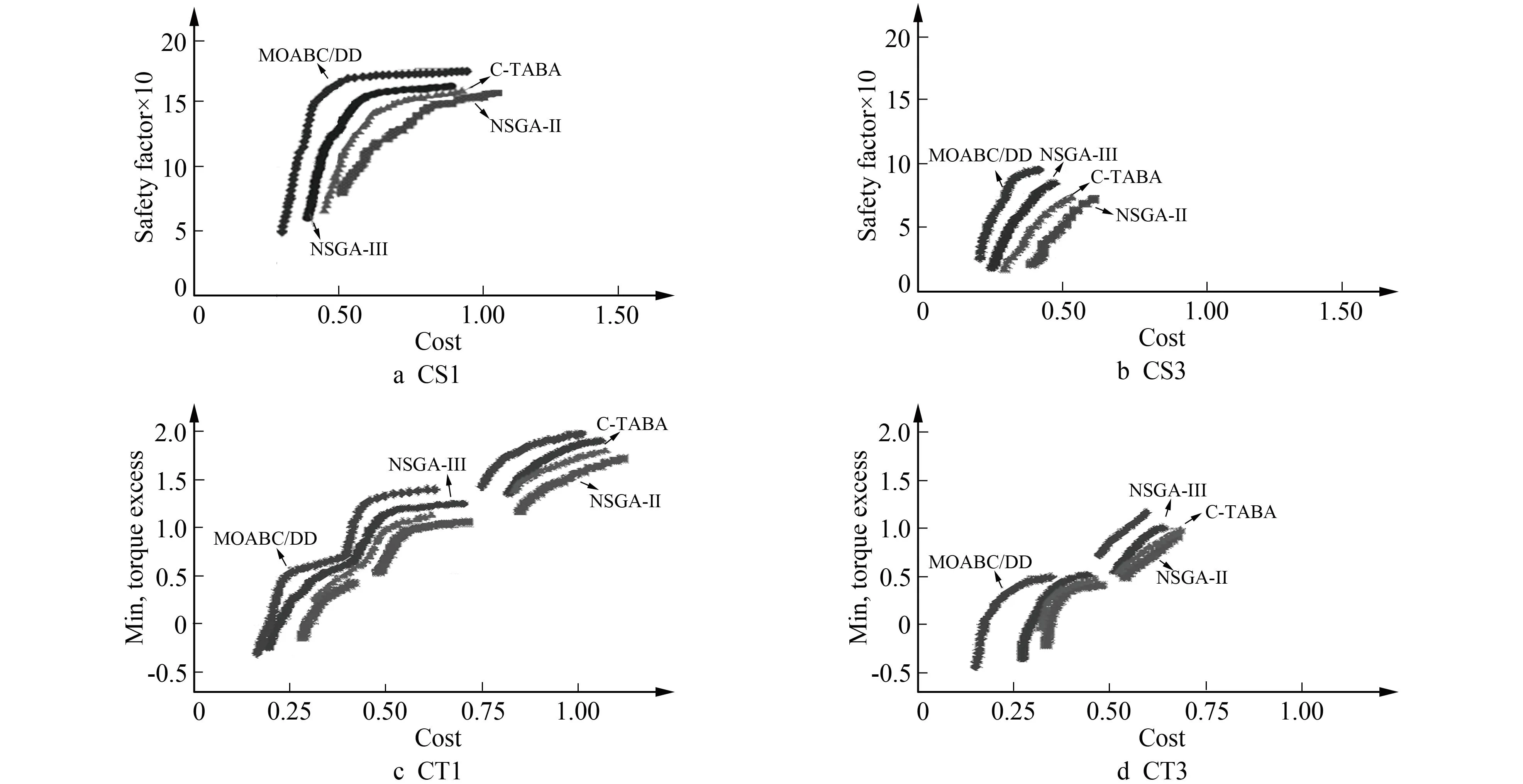
4 结 语
