基于强化学习的木工送料平台误差控制研究
2023-12-25孟兆新乔际冰
朱 莉 王 猛 孟兆新 李 博 乔际冰
(东北林业大学机电工程学院,黑龙江 哈尔滨 150040)
我国在木材零部件切割加工方面大都还使用人力手推切割,这种方式生产效率低,劳动强度大,且危险性较高[1]。由于送料平台属于多自由度多耦合控制系统,系统模型的构建较为困难,各轴的误差也会影响终端切割误差。目前,调整机构误差的控制方法主要有改进机械结构进行补偿[2]、提前反转减小回程误差等[3]。然而,在切割不同曲线时,需要对参数进行调整,因而使加工过程中的操作变得复杂。
由于通过机械结构减小误差的方法效果有限,近年来,通过软件控制机械结构误差的方法成为研究热点。Ni等[4]为实现三自由度机械手的误差控制系统,使用一阶摄动理论辅助建立了误差矩阵。Pan等[5]建立了一种新的误差控制机制,减小了不确定N-link机器人系统的误差。Yang等[6]在研究机器人运行轨迹方面使用了误差约束方案。在控制方法中,智能控制中的机器学习方法只需利用智能学习中产生的数据决定行为[7]。强化学习则是一种试错学习算法[8],在缺乏数据指导的情况下,通过智能体与环境的不断交互来提高整体性能,从而达到目标范围或找到最优控制策略。在强化学习中,使用较多的Q学习算法已被用于主动结构控制系统中[9],可对相关参数进行在线调整。但是在控制连续动作时,有时不能达到超精密减振范围。因此,在连续动作的控制中,确定性策略梯度(DPG)算法[10]被广泛使用。
鉴于机器学习近三十年来的进展[11],将深度神经网络(DNN)[12]与强化学习(RL)[13]相结合,进而形成的深度强化学习(DRL)已成为研究热点。与传统的RL相比,DRL通过利用DNN的能力估计RL中的关联函数,从而有助于更精确地收敛和逼近[14]。这些算法在多个领域都有了一定的应用。同时,为了使强化学习算法与实际工程有更高的契合度,研究人员对算法进行了进一步优化。例如,Nagabandi等[15]使用了一种基于模型的深度强化学习方法,只需17 min的训练样本,就可以让六足机器人成功跟踪所需的直线轨迹。然而,其训练环境范围小,导航路径短,训练结果仅适用于目标点的跟踪。Kiran等[16]对深度强化学习算法进行了总结,并提出了行为克隆、模仿学习、逆强化学习等相邻邻域的应用。由于设计机器人的控制设计复杂,Kober等[17]分别研究了基于模型和无模型、基于价值函数和基于策略搜索方法间的选择,为机器人的控制提供了框架。Peng等[18]使用多智能体深度确定性策略梯度解决了分布式优化问题,以最大化卸载任务数量,实现了无人机辅助车载网络的多维资源管理。Wang等[19]提出了一种基于深度强化的轨迹控制算法(RAT),应用优先体验回放(PER)来改善训练过程的收敛性。近似策略优化(PPO)[20]使用了一阶优化算法,并简化了代理目标函数的约束限定,更加易于实现。
综上所述,本文使用深度确定性策略梯度算法,使智能体通过对各个状态的分析,依靠神经网络做出相应的决策,并对每个状态的不同决策做出相应的价值评估。由于各轴与连杆之间耦合关系复杂,为保证整个试验的安全进行,首先使用多体动力学软件(ADAMS)、矩阵实验室(MATLAB)软件进行建模仿真,在达到允许的误差范围后,进行数据迁移,并采用实际送料平台进行验证。研究结果可为提高锯切木材送料平台的运动姿态精度提供参考。
1 误差分析
1.1 送料平台结构分析
由旋转机构简图1可得各轴丝杠的有效行程和初始位置。为了解算出平台旋转机构解析数学算式,根据几何关系和板材特性[21]可以得到各个时刻滑块坐标与偏转角度之间的相对应关系。由于所有的滑块位置只受目标曲线的影响,且每个时刻的值只受偏转机构的偏转角θ的影响,因此机构中连杆与所在支链中连杆AD、BE和CF与丝杠的夹角可以分别表示为下式:
式中:α1、α2、α3为连杆偏转角度,(°);θ为夹具偏转角度,(°);c为夹具固定螺母B距E轴丝杠距离,mm;LAB为夹具固定螺母A、B两点距离,mm;yD、yE、yF分别为滑块到丝杠首端的距离,mm;a为相邻丝杠的距离,mm;ly为锯切点到丝杠首端的距离,mm。
通过求解转角机构各支链的方程组,计算送料平台转角机构三个滑块的输入位移,建立数学表达式如下式:
式中:LAC为夹具固定螺母A与C距离,mm;LBC为夹具固定螺母B与C距离,mm;LAD、LBE、LCF分别为D、E、F三轴连杆长度,mm。
依据上文送料平台运动学分析的机构解算方程式并参考文献[22],得出本研究仿人工送料平台动力学系统的数学模型:
式中:Qn为输入广义驱动力矩矢量和,其大致由4个部分组成,分别对应螺母部分、连杆部分、夹具及被加工件部分和丝杠部分;mi为相应各部件的质量,其中mn为螺母部分质量,g;mln为连杆部分质量,g;mf为夹具等部分质量,g;msn为丝杠部分质量,g;qn为广义坐标(滚珠丝杠螺母滑块位移),即q1=LA,q2=LB,q3=LC,q4=LD,q5=LE。D为直径,mm;l为杆长,mm;Pn为丝杠导程,mm;kn为连杆动能系数;h、w分别为夹具的长和宽,mm;n为轴数(n=1、2、…、5)。
1.2 送料平台误差分析
送料平台的误差来源可分为静态误差和动态误差。静态误差是由于部件的生产和安装原因引起的,包括丝杠螺母副的螺距误差和各轴与动平台之间的传动误差。如图1所示,系统主体由电机、丝杠、滑块、连杆和夹具组成,其中存在一定的耦合关系,会导致静态误差的放大。动态误差主要由机构工作过程中各部件的形变和磨损导致。其中,最主要的是滑块与丝杠之间的反向间隙误差,随着机构运行,误差不断累积。
控制系统要实现对送料平台的精准控制,必须保持稳定状态,但交流电压的波动会导致执行机构出现误差。静态误差可以通过校准的方法减小;动态误差主要由回程误差组成,可以通过程序控制电机在改变转动方向时提前反转进行减小;控制误差和运行时的能量来源、电机属性相关,在不同环境内产生的误差大小也不同。
1.3 偏转机构误差关系分析
本文旨在通过控制各轴误差来减小终端误差,通过设计得到各个轴的滑块运动轨迹曲线后,分别通过人工调试和PID控制进行试验,得到各个轴的误差以及最终切割曲线的Y方向的跟踪误差。分别取D、E轴的误差和终端切割曲线X、Y方向上的误差进行分析。如图2所示,图a为通过人工调试的试验误差,误差范围为±(-2.325~3.314) mm,误差最大值分布在D、E两轴正负误差最大的情况,且随着误差的减小呈下降的关系。图b为PID控制的D、F两轴与终端跟踪误差关系,通过误差补偿,可将误差范围缩小至-1.2~1.8 mm。对比可知,两者变化趋势相似,且整体误差有所下降。图c和图d中X轴向误差与Y方向误差变化趋势相似,X方向的误差保持在0.666 mm以下,对切割轮廓误差影响很小。

图2 D、F与终端跟踪误差分布图Fig.2 Distribution of errors in axes D, F, and terminal tracking error with PID compensation
图3为E轴误差与终端误差进行比较,误差分布范围广,主要在E轴误差较小的情况下聚集,这是由于终端误差较大的情况较少,没有明显拟合关系。


图3 E轴误差与终端跟踪误差分布图Fig.3 Distribution of errors in axes D, F, and terminal tracking error with PID compensation
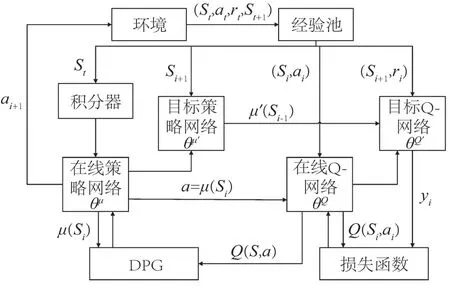
图4 基于DDPG-IC的控制算法框架Fig.4 Control algorithm framework based on DDPG-IC
根据以上误差分布图像可以发现,整个机械系统的终端误差与偏转机构的D轴和F轴的误差大小存在紧密联系,但和定点轴E的关系不明显。因为D轴和F轴的主要作用是调整偏转角度,使切割方向和锯条方向相同。E轴的主要作用是辅助X、Y轴实现定点需要。因此,通过减小滑块误差来调整终端误差是可行的。
2 控制方法研究
2.1 强化学习
2.1.1 马尔可夫决策过程
强化学习过程实质上是马尔可夫决策过程,即系统的下一个状态只和当前状态有关。P是状态转移矩阵,表示了从t时刻状态s经过智能体决策后做出行动,到达下一时刻状态s'的可能性。R是奖励函数,表示运动到s'状态后与预计状态的误差。整体表示为
式中:γ∈(0,1]为衰减系数,γ趋向于0代表短视在乎眼前收益,γ趋向于1代表偏重考虑远期收益。
2.1.2 基于策略的强化学习方法
因为本文研究的送料平台属于连续动作且需要使用随机策略,所以采用基于策略的强化学习方法。基于策略的强化学习算法不依赖价值函数,而是通过评价策略的可优化的目标函数对策略进行优化。在基于策略的方法里,策略可以表示为连续函数:
式中:θ为连续函数的参数,不受值函数的约束。而策略的性能需要由策略目标函数进行评价。策略目标函数选择所有状态值函数的加权平均值,表示为:
2.2 深度确定性策略梯度算法
在送料平台控制问题中,目标是设计稳定高效的控制策略,使每个轴上的滑块位置尽快达到目标位置的误差范围之内,因此采用奖励值rt来表示各轴滑块当前状态与目标状态的距离,将每一步的策略目标函数定义为:
由确定性策略梯度定理[23],策略目标函数关于策略参数的梯度为:
式中:ρAµ为变化的控制策略,Aµ得到的状态分布QAμ(s,a)是Aµ所对应的状态-动作值函数。
值函数需要通过Q学习方法进行拟合,时间差分误差可以通过状态转移矩阵得到:
采用随机梯度下降的方法调整参数,最小化时间差分误差,即可逐步提高状态-动作值函数的拟合精度。由于算法给定的动作是确定的,通过每个轴在理想情况下的运动方程对其进行了限制,所以在部分状态下控制策略是确定的。为保证算法的探索性能,执行者输出上叠加一个高斯噪声,探索策略表示为:
为解决系统模型的复杂性和部分耦合问题,采用神经网络对实际值函数和状态-动作值函数进行拟合[24],系统的网络结构包括执行网络和评价网络两部分。执行网络通过经验池和评价网络的输出,计算五个归一化电机控制量来控制送料平台。评价网络则通过环境状态拟合动作-值函数。两个目标网络使用相同的软件方法进行更新,而在线Q网采用均方误差作为损失函数,并以获得Q值的最大值为目标更新参数。在线策略网通过训练小批量数据来更新网络参数,并利用蒙特卡罗方法实现无偏估计。这些方法可以提高训练的稳定性和速度。
2.3 最小安全距离约束
智能体决策与五个丝杠上滑块的位置相关,当滑块因为连杆和夹具的机械关系使电机无法按照决策运动时,电机会卡死。为确保强化学习的决策安全可靠,本文采用最小安全距离的方法来约束控制器的反应。使用反向解算得到每个轴在理想情况下的运动轨迹,然后添加一定程度的误差进行正向解算,得出系统能接受的最大误差εmax,将决策后每个轴的误差限制在ε≤εmax以避免系统出现卡死状况。这种方法可以正向影响奖励函数,加快强化学习的收敛过程并确保系统的安全性。
2.4 算法步骤
算法伪代码:
初始化执行网络参数Aµ,评价网络的权重Q和σ
初始化经验缓存区R
for训练节数=1 to最大训练节数 do
初始化探索噪声序列N(0,σ2)
清空积分补偿器,接收初始状态信号s1
for时间步t=1 toTmaxdo
计算控制量at
送料平台电机执行控制量at
获取新状态信号st+1和奖励值rt
将经验(st,at,rt+1,st+1)存入经验回放池R
从经验回放池R中随机抽取一批经验{e1,e2,...,eN}
计算评价网络参数的梯度:
更新评价网络权值
更新策略网络和目标网络参数
ifst+1超过安全范围 then
Break
End for
End for
3 仿真试验
为验证DDPG算法的有效性,使用NX进行模型参数设计[25],利用MATLAB和ADAMS进行仿真平台的搭建,模型如图5所示。加入连接和状态变量后导出,在siulink中设置为环境,具体参数如表1所示。

表1 偏转机构零件尺寸Tab.1 Dimension of deflection mechanism components

图5 送料平台仿真模型Fig.5 Feeding platform simulation model
3.1 超参数设计
实验中的超参数设计如表2所示。

表2 DDPG-IC算法训练参数Tab.2 Training parameters for DDPG-IC algorithm
3.2 奖励函数设计
在强化学习的过程中,奖励函数作为实时反馈,对算法的决策选择和收敛速度有着很大的影响。假设送料平台和带锯机在某一时刻t,环境状态为s,每个轴的位置滑块的信息XD、XE、XF、XX、XY。木工带锯机送料平台的状态包括各轴的实时位置和滑块的运动速度。初始状态下,将X、Y轴归零,D、E、F三轴分别初始化至初始切割点处的偏转角度,将切割连续动作离散化,分为采样点,在每个采样处的状态通过光栅尺采集各轴滑块位置。
奖励函数的设置影响整个算法的收敛速度,并且与智能体的决策存在关系。本文的奖励函数由各轴的跟踪误差大小确定。根据图1和各轴误差分析,D轴和E轴的主要作用是偏转机构的角度确定,与终端跟踪误差关系密切,所以奖励函数设计为:
3.3 回合终止条件设置:
1)送料平台机械结构出现卡死状况。
2) 丝杠跟踪误差大于6 mm时,此时的状态相对而言并不能指导有效学习,反而会增大计算量。
3) 达到训练最大步数。
4 仿真结果分析
4.1 仿真结果
仿真结果如图6所示。由图可知,两种曲线在初始阶段都处于较低水平,因为在该阶段送料平台的奖励反馈只来源于机械结构卡死状况之前所给予的奖励。由于常数值设置偏小,因而出现了累积奖励值下降的情况。图6(a)在仿真达到1 000回合时,有效学习的速率加大。在大约1 500回合时,出现了明显的收敛现象,此时整个仿真过程可以完成,但仍在探索最优解。相对于图b更早达到有效学习状态,收敛速度快且稳定。
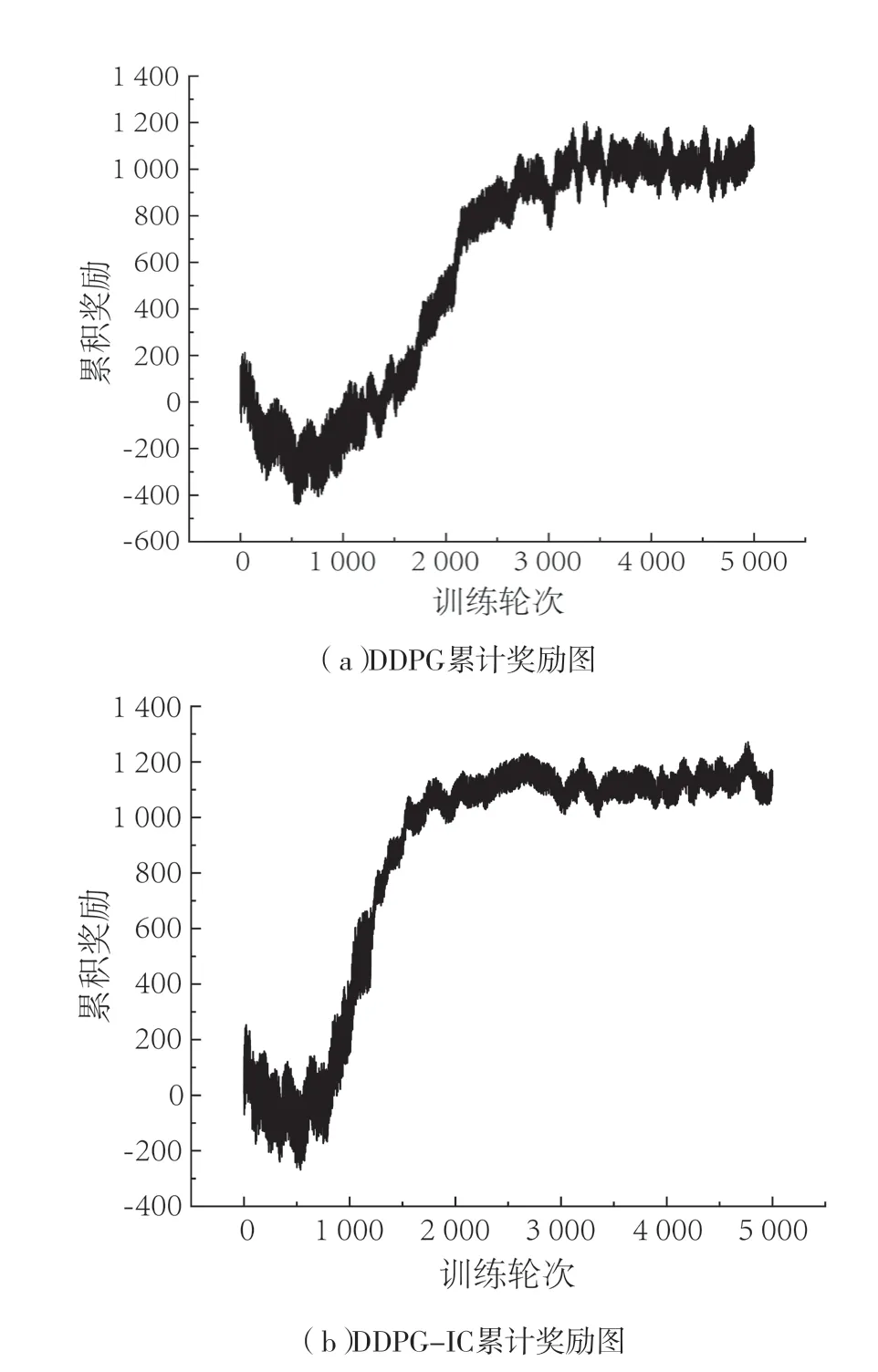
图6 确定性策略梯度仿真奖励变化折线图Fig.6 Line chart of reward variation in deterministic policy gradient simulation
在仿真达到稳定后,进行数据迁移[26],使用codesys控制ADAMS模型进行虚轴模拟试验。控制方法选取三种,分别是无误差矫正手段、PID控制和强化学习得到的控制手段。图7分别表示偏转结构三轴的位移。由于强化学习将各轴误差作为奖励函数进行限制,所以各轴的误差相比于其它两种方法实现了跟踪误差的控制。与PID补偿方法相比,各轴误差分别减小了33.82%、65.23%和43.73%,但各轴的回程误差以及累计误差在滑块发生转向时仍有较大的影响,最大误差在此处表现出来。
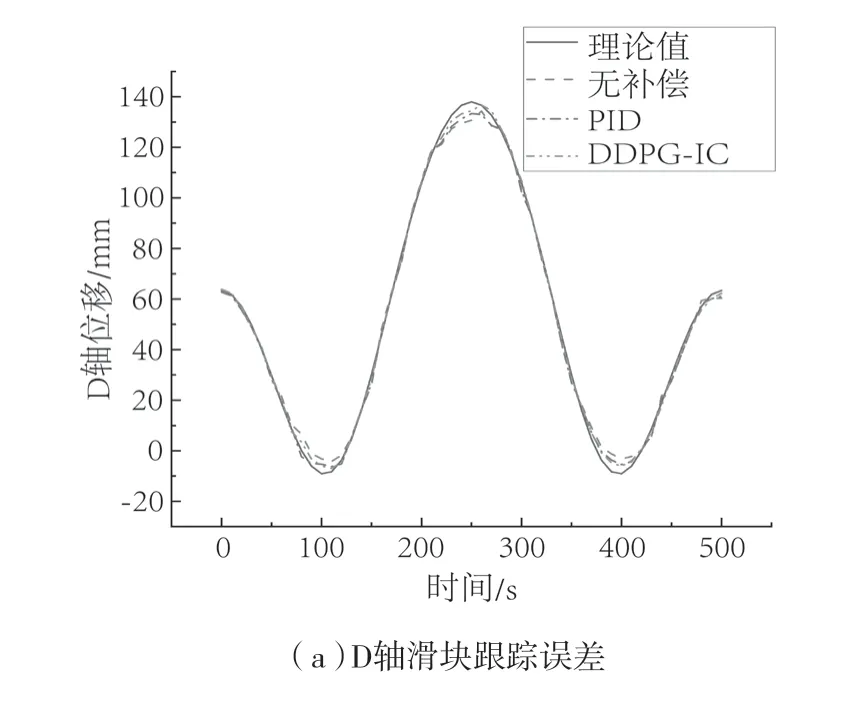

图7 偏转机构滑块仿真位移曲线Fig.7 Simulation displacement curves at the terminal
图8 和图9 为试验终端的跟踪误差。相比于未补偿控制有了较大的提升,只在部份区域产生波动,整体还是与D轴和F轴的误差大小有明显的增减关系。终端最大误差达到0.85 mm,比PID误差控制提高了63.97%,并保持在较小的范围。
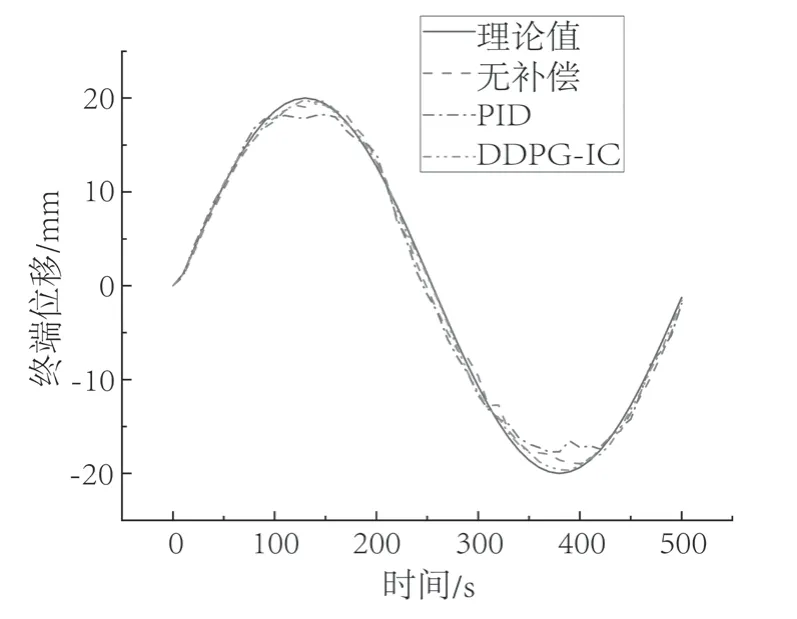
图8 终端位移图Fig.8 Terminal displacement
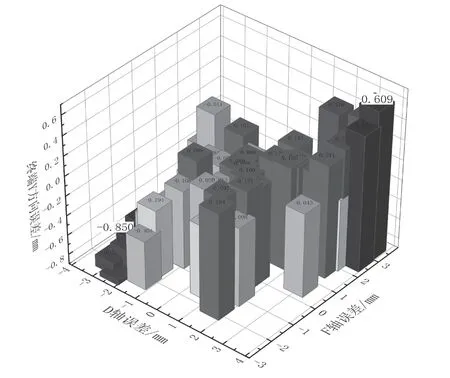
图9 终端Y方向跟踪误差Fig.9 Terminal Y-axis tracking error
5 结论
本文采用深度强化学习算法,以达到对送料平台各轴的跟踪误差的控制进而控制终端误差。结果表明,原始DDPG算法与加入积分的算法都可以达到效果,但由于加入了最小安全距离限制和积分补偿,其收敛速度和稳定性得到了一定的提高。测评结果显示,在足够回合数的学习情况下,两种方法都能够达到稳定并保持良好的控制效果。使用MATLAB和ADAMS进行联合仿真,可以提高送料平台的控制精度。在仿真试验中,也可以实现误差的减小,且误差的控制难点还是在于累计误差和回程误差在拐点时的释放,在此处会出现误差峰值。
本文在仿真试验中只研究了送料过程,后续可将带锯机的锯条转速或辅助盘转矩作为限制条件加入价值函数。由于仿真模型和实体送料平台所受环境影响和误差分布的不同,需要对实体模型进行强化学习。同时,使用仿真数据可以加快学习进程,防止机器出现故障。
