基于混合优化算法的超参数优化方法及其应用

作者简介：丁彧洋（1997-），硕士研究生，从事深度学习、时间序列分析的研究，6201905018@stu.jiangnan.edu.cn。

引用本文：丁彧洋.基于混合优化算法的超参数优化方法及其应用[J].化工自动化及仪表，2023，50（6）：000-000.

DOI：10.20030/j.cnki.1000-3932.202306000

摘  要  卷積神经网络（CNN）自身结构的超参数对于分类问题中的准确率与效率有较大的影响，针对现有超参数优化方法多依赖传统组合，优化结果不彻底，导致模型分类效果不佳的状况，提出一种基于混合优化算法的CNN超参数优化方法。该方法根据CNN架构的结构特点选取超参数，然后采用粒子群优化算法（PSO）-梯度下降（GD）混合算法进行优化。在测试数据集上的实验结果表明：该方法在分类问题上具有较好的性能，提升了超参数的优化效率，避免了传统PSO算法易陷入局部最优的缺点。

关键词  PSO-GD混合算法  超参数优化  CNN  分类性能  优化效率  局部最优

中图分类号  TP183      文献标志码  A      文章编号  1000-3932（2023）06-0000-00

现阶段，信息分类技术已经发展得比较成熟，适用于不同场景的卷积神经网络（Convolutional Neural Network，CNN）架构[1～4]层出不穷，但复杂的CNN结构往往耗费硬件资源及计算成本。CNN用于分类任务训练前，需提前设置好CNN内部的一些参数（即超参数），选取一组最优超参数可以在不改变CNN结构的前提下最大程度地提升CNN的分类性能。因此，选定适合的超参数将CNN架构的分类性能完全释放出来，在工程实践中具有极其重要的作用和意义。

相关CNN超参数优化方法的研究已经有一些成果，早期研究集中于将机器学习的超参数优化方法用于CNN[5]。超参数优化方法主要分为无模型优化和基于模型的优化，目前，前者最先进的方法包括简单的网格和随机搜索；后者包括基于种群的启发式优化算法，以及基于高斯过程的贝叶斯优化（GP）[6]。启发式优化算法对于CNN超参数优化尤为值得关注，其中粒子群优化算法（Particle Swarm Optimization，PSO）[7，8]由于其简单性和通用性已经被证明在解决许多区域中的多任务方面非常有效，并且它具有大规模并行化的巨大潜力。基于PSO的超参数优化，其搜索效率远超网格搜索、随机搜索等，缩短了超参数优化的搜索时间，解决了传统超参数优化效率低、耗时长等问题。但PSO也存在易陷入局部最优的问题，这会造成超参数优化停留在局部最优而非全局最优的一组超参数，在一定程度上无法搜索到使CNN性能达到最优的一组超参数，从而无法使CNN处理分类问题时达到最理想的结果。由此，混合优化算法合成为新趋势之一，通过将不同的元启发算法进行结合，综合不同元启发式算法的特性，使混合算法拥有更快的寻优速度或更好的寻优特性。文献[9]探索了一种遗传算法+PSO的混合算法，该算法对优化问题有显著效果；文献[10]提出一种模拟退火和梯度结合的混合算法，该混合算法为模型提供了概率爬坡的能力，在不牺牲模型收敛效率和稳定性的情况下具有更好的泛化效果。如今，混合算法更倾向于针对具体问题进行混合和改进，文献[11]为特征选择问题提出一种混合灰狼优化和粒子群优化的二进制形式算法，用以获得更优的特征性能指标和使用精度；文献[12]针对具有有限函数计算的计算成本数值问题，提出混合萤火虫和粒子群优化算法，通过检查前期的全局最佳适应度值，正确确定了本地搜索过程的开始点位。

笔者提出一种基于粒子群优化算法（PSO）-梯度下降（Gradient Descent，GD）混合优化算法的CNN超参数优化方法，根据CNN的架构特点选取卷积层与池化层的结构参数，以避免传统PSO对超参数的优化停留在局部最优的弊端。

1  CNN及其超参数优化算法

1.1  CNN

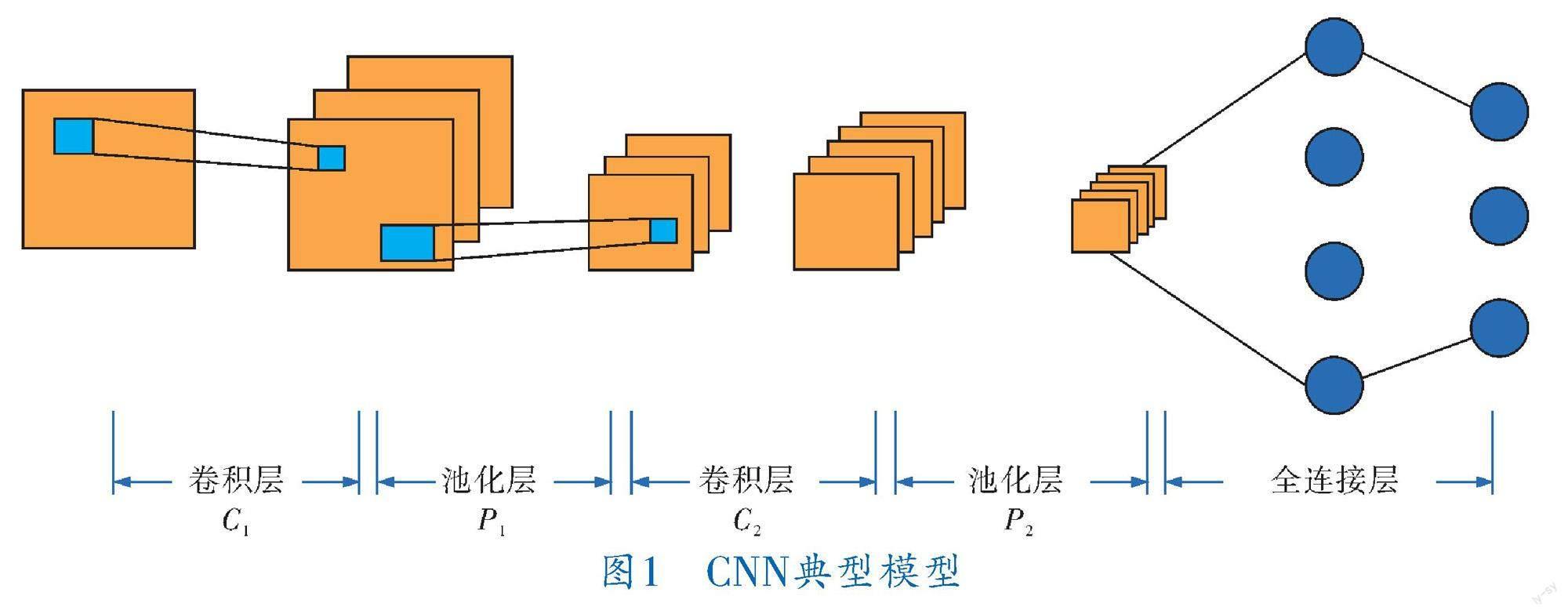
CNN作为前馈神经网络，其概念主要来自信号处理领域的卷积，实际表征了输入与输出间的映射关系，典型模型如图1所示，其结构主要包括卷积层、池化层以及激活函数等，由卷积层对输入值间存在的耦合关系进行处理，激活函数保证整个模型能够较好地拟合非线性函数，而全连接层则进一步提高网络的拟合能力。

1.2  混合智能优化算法

混合智能优化算法是将启发式算法与梯度算法相结合，其本质上是随机的，因为它依赖于启发算法绕过局部极小值，类似于对未知数的连续随机扰动，并且能够以正概率“逃离”任何陷阱。同时，对于小邻域，它能以极快的速度收敛到局部极小值，大幅提高随机优化算法的搜索效率和收敛速度。

由于PSO始于解的一个种群（多点）而非单个解，因此具有更好的全局寻优能力。采用概率而不是确定的状态转移规则，能自适应地调整搜索方向，因此能更好地跳出局部最优点。而GD算法则采用负梯度作为极值的搜索方向，以便能够在搜索区间内最快速下降，这样与初值点选取的好坏关系减小，又由于GD算法每次的迭代计算量小，在经过有限量次迭代后目标函数值都能够大幅下降、程序简短，并且占用较少的时间资源和运算资源。因此，笔者将两种算法结合，提出PSO-GD混合优化算法，其流程如图2所示，先采用GD算法找到局部最优点，再采用PSO算法寻找最优解。同时，如果算法陷入局部最优点，PSO能跳出局部最优点再次寻找全局最优点。

2  基于PSO-GD算法的CNN超参数优化方法

2.1  算法基本原理

根据图2所示的完整算法流程，可大致将PSO-GD混合智能优化算法描述为：

a.随机生成并评估。令迭代数。

b.通过基于梯度的最小化方法求解局部最小值，并作为初始猜测给出，，其中，是阈值，设定为接近零值的正参数。

c.从开始，执行次模拟粒子群发散直到获得一个点，使得对于误差精度满足。

d.。回到步骤b循环，直到收敛。

在算法的步骤c中，模拟的粒子群迭代由4个关键步骤组成，即：

a.下一个实验点主要是由已知解的附近空间的粒子运动产生的；

b.将粒子群个体特征转换为二进制数字，确定它们的值范围和边界条件；

c.通过改变新一代分布来控制是否跳出局部最优极限；

d.结合粒子群变异和交叉的特点，在迭代过程中获得最适合个体的最优解，终止迭代并输出最终结果。

2.2  算法收敛性分析

2.2.1  标准PSO算法的全局收敛性

首先描述PSO的迭代过程：

a.初始化，随机查找且设；

b.从已有的粒子值中随机生成新的极值；

c.设，再选择，设（其中（·）为迭代函数，，且是的任意Borel子集），返回步骤b迭代。

条件1  ，并且若，则有。

条件2  对中的任意Borel子集，且，有。

定理1  PSO算法不满足条件1。

定理2  PSO算法不满足条件2，不能保证全局收敛性。

因此可得出结论，该算法作为随机搜索算法，当粒子尚未搜索到最优区域时，粒子的发散速度就可能已经失去动力，进而导致无法跳出局部最优，即不能得到全局最优。而从整体来看，应该分析最优保持操作，所以最优保持操作需由梯度算法实现，从而需要进一步分析梯度算法得出的结果。

2.2.2  GD算法的收敛性

首先，由数学理论可以得到以下定义和定理。

如果标量函数满足如下条件，称其满足Lipschitz连续性条件：

（1）

其中，为Lipschitz常数。对于固定的，是一个定值。这个条件对函数值的变化做出了限制。

如果函数的梯度满足值为的Lipschitz连续，称函数为平滑：

（2）

这个条件对函数梯度的变化进行了约束：梯度之差的模长不会超过自变量之差模长的常数倍。满足平滑的函数有如下性质：

（3）

如果函数为凸函数，过的切线在曲线下，则有：

（4）

进而。

因此得出平滑具有两个性质：

（5）

（6）

首先证明GD算法的自变量的新解比当前解更接近最终解。考虑新解到最终解的距离：

（7）

利用平滑的第2点性质（即式（6）），考虑在点的线性拟合：

（8）

由于为最终解，则有：

（9）

（10）

（11）

代入式（7），有：

（12）

显然，只要学习率，就可以保证：

（13）

然后，考虑两次迭代的函数值：

（14）

插进最优解的函数值，比较两次迭代距最优点函数值的距离：

（15）

利用凸函数性质以及柯西-施瓦茨不等式，构造一个关系：

（16）

（17）

代入式（15）可得：

（18）

从之前的证明可以得到，于是除去分母中的，则有：

（19）

然后两边同时除以正数得到：

（20）

然后对式（20）从0～t-1进行累加：

（21）

由于：

（22）

所以：

（23）

由此證明完毕，即算法的收敛性成立。

2.3  CNN超参数优化建模

首先对需要分类的数据集进行预处理，并将其按比例划分成训练集T、测试集和验证集V，其中验证集是从训练集中提取的，满足。

在准备工作完成后，开始搭建CNN架构，包括卷积层、池化层、卷积层、池化层，最后由Softmax激活终止。根据CNN架构的结构特点，选取卷积层C1和池化层P1的结构参数为后决定的超参数，并确定这组超参数的取值范围为。

而后在验证集V上采用PSO-GD混合算法优化CNN架构的超参数，可得一组对应的超参数值，整个超参数优化过程设计到的相关变量见表1。

在第次迭代时，每个粒子更新自己的速度和位置：

（24）

（25）

其中，为惯性因子，和为学习因子，均为自选常数；和是范围内的随机数。

随后选择全局变异算子对整个群体中的所有粒子的位置进行变更，或者选择局部变异算子对群体中的精英粒子的位置进行变更。全局变异算子与局部变异算子对位置变更的公式为：

（26）

（27）

其中，是波动因子；为范围内的随机数；为精英粒子；是由局部变异算子生成的新粒子的数目；为全局变异频率；为局部变异频率。

之后，检查粒子速度和位置是否越界，若越界则以其超出的边界值取代相应的粒子值。设为粒子的速度范围，为粒子的位置范围。具体判断方法如下：

a.若，則；

b.若，则；

c.若，则；

d.若，则。

根据上述限制条件确定的最优位置即所要求的超参数值。将超参数输入到CNN中，并用最初得到的训练集对优化后的CNN进行训练，而将初始步骤得到的测试集输入训练好的CNN中，可以得到最终结果。

随后根据条件，判断迭代是否达到终止条件。

首先计算各个粒子的适应度函数值：

（28）

其中，为先前阶段得到的分类结果的准确率。

通过式（28）得到的本次迭代的各个粒子适应度函数值，分别更新个体历史最优位置和群体最优位置，得到本次迭代最优粒子：

（29）

（30）

判断最优粒子的适应度值增加小于阈值，判断群体中的最佳粒子位置更新小于最小步长，判断迭代次数是否达到最大迭代次数，若满足上述终止条件之一，则终止迭代。如果没有达到终止条件，则重新代回超参数值确定步骤起始段继续流程，如果达到终止条件，得到最终的最优超参数，记为，并将其代入到CNN结构中，对整个数据集的进行分类，得到最终结果。

3  仿真实验与结果分析

为了验证基于PSO-GD混合优化算法的CNN超参数优化方法的性能，选取两个基准测试数据集进行实验仿真，其中手写数字识别MNIST数据集的片段如图3所示，该数据集有70 000个灰度图像，每个图像像素为28×28，其中包含10个类别，每个类别有7 000个图像；随机选取该数据集中的60 000个图像作为训练集，剩余的10 000个图像作为测试集，从训练集中随机挑选出6 000个图像作为验证集。

物体识别cifar-10数据集的片段如图4所示，该数据集有60 000个32×32像素的彩色图像，其中包含10个类别，每个类别有6 000个图像；随机选取该数据集中的50 000个图像作为训练集，剩余的10 000个图像作为测试集，从训练集中随机挑选出5 000个图像作为验证集。

3.1  MNIST数据集实验

将混合优化算法中的参数定为粒子搜索空间维度，粒子个数，惯性因子，学习因子，阈值，最小步长，判断迭代次数。搭建CNN架构，选取卷积层C1和池化层P1的结构参数为超参数，确定这组超参数的取值范围，见表2。

在算法结构中，将输出结果以适应度函数的值进行表示，由于过程包含收敛性的分析，因此整体结果按相反数取值，因此，适应度函数值越大，分类效果越好。

MNIST数据集的分类结果如图5所示。

3.2  cifar-10数据集实验

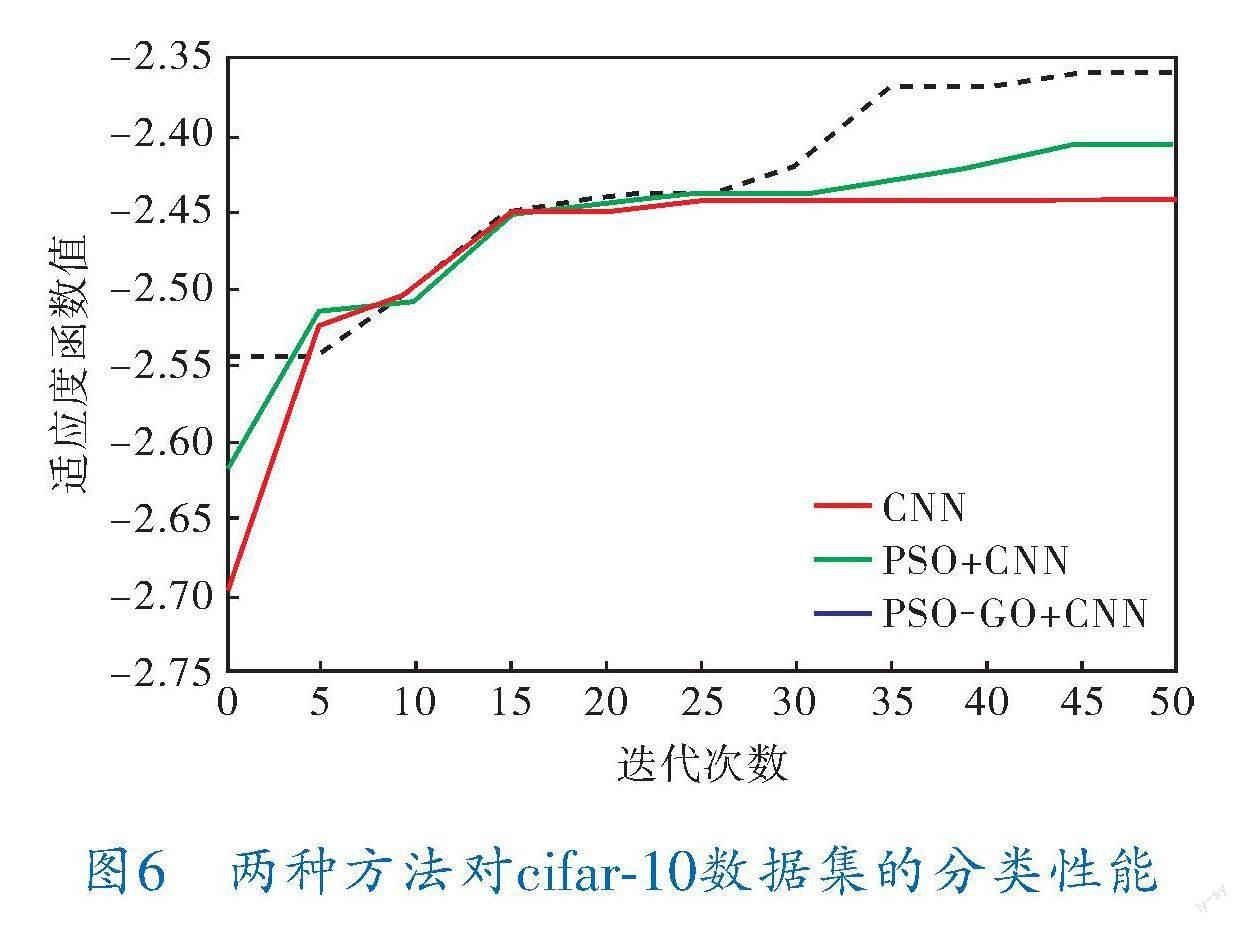
实验所选取各参数与MNIST数据集实验相同，分类结果如图6所示。

对比图5、6可以看出，无论是超参数优化前的常规CNN，还是PSO、PSO-GD优化超参数后的CNN，随着迭代次数的增加，优化都在逐步进行，分类误差不断减小，而经过超参数优化后的方法，在分类准确性上有所提高。

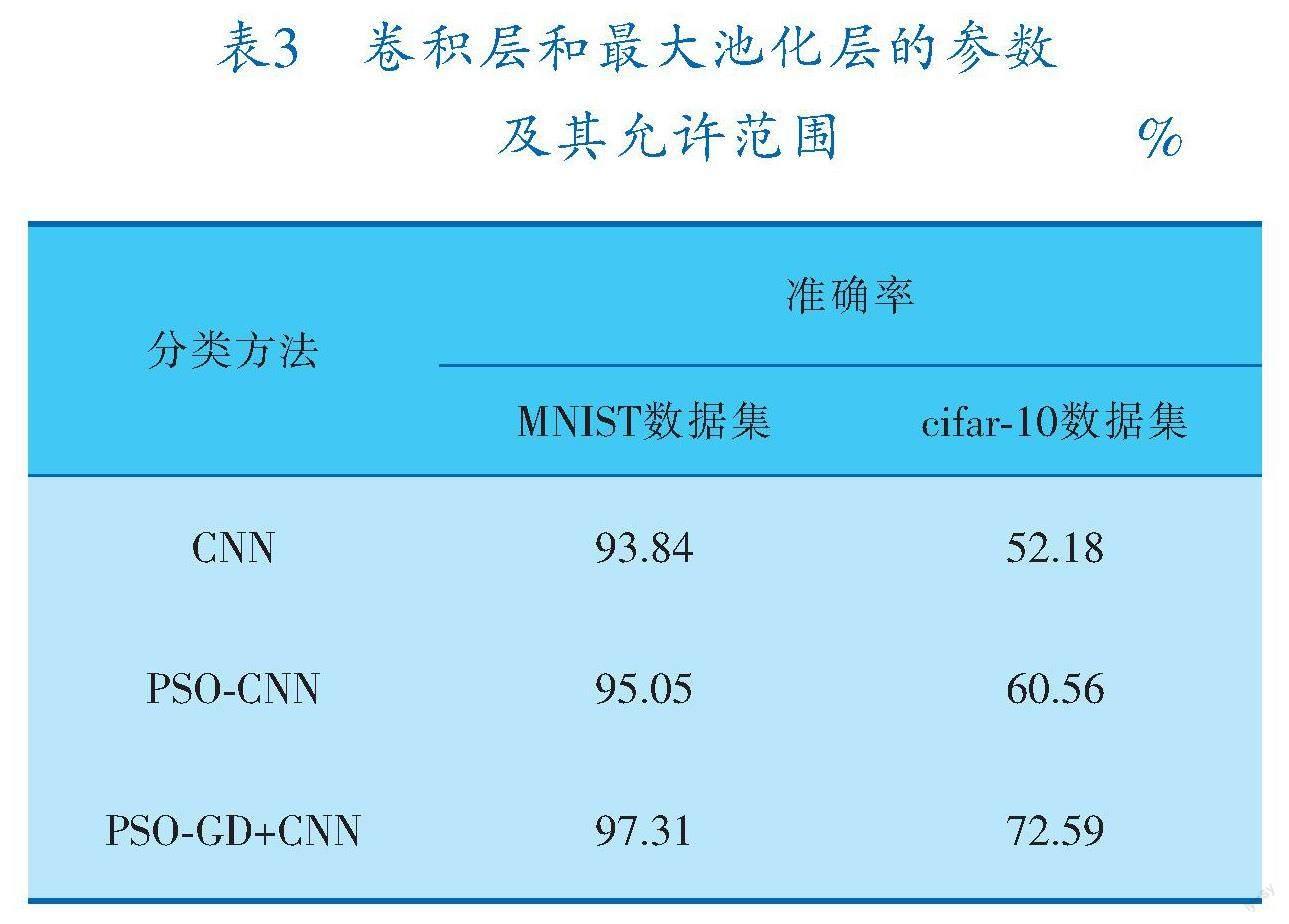
超参数优化方法改进前后手写数字识别MNIST数据集和物体识别cifar-10数据集图像分类准确率对比见表3，可以看出，PSO-GD混合优化方法在不改变分类CNN架构的前提下对图像分类准确率有一定程度的提升，最大程度地发挥了CNN架构的图像分类潜力，节约了CNN进行图像分类时的硬件资源及计算成本。

4  结束语

利用PSO的全局搜索性能融合GD算法的快收敛性，提出基于PSO-GD混合优化算法的超参数优化方法，对CNN结构中的超参数进行了优化，并通过典型的测试数据集对其分类性能进行了评价。实验结果表明，该方法与优化前相比，具备了更好的跳出局部最优限制的能力，最大程度地发挥了CNN架构的分类潜力，节约了CNN进行分类任务时的硬件资源及计算成本，该方法具有一定工程应用价值。

参  考  文  献

[1] SIMONYAN K，ZISSERMAN A.Very deep convolutional networks for large-scale image recognition[C]//Proceedings of  the  3rd  International  Conference  on  Learning Representations.San Diego：ICLR，2015：1-14.

[2] KRIZHEVSKY A，SUTSKEVER I，HINTON G E.Imagenet classification with deep convolutional neural networks[J].Communications of the ACM，2017，60（6）：84-90.

[3] GIRSHICK R，DONAHUE J，DARRELL T，et al.Rich feature hierarchies for accurate object detection and semantic segmentation[C]//Proceedings of the IEEE conference on computer vision and pattern recognition.2014：580-587

[4] REDMON J，DIVVALA S，GIRSHICK R，et al.You only look once：Unified，real-time object detection[C]//Proceedings of the IEEE conference on computer vision and pattern recognition.2016：779-788.

[5] ANDONIE R，FLOREA A C.Weighted random search for CNN hyperparameter optimization[J].arXiv preprint arXiv：2003.13300，2020.

[6] WU J，CHEN X Y，ZHANG H，et al.Hyperparameter optimization for machine learning models based on Bayesian optimization[J].Journal of Electronic Science and Technology，2019，17（1）：26-40.

[7] WANG D，TAN D，LIU L.Particle swarm optimization algorithm： an overview[J].Soft computing，2018，22：387-408.

[8] SALLEH I，BELKOURCHIA Y，AZRAR L.Optimization of the shape parameter of RBF based on the PSO algorithm to solve nonlinear stochastic differential equation[C]//2019 5th International Conference on Optimization and Applications （ICOA）.2019：1-5.

[9] GHORBANI N，KASAEIAN A，TOOPSHEKAN A，et al.Optimizing a hybrid wind-PV-battery system using GA-PSO and MOPSO for reducing cost and increasing reliability[J].Energy，2018，154：581-591.

[10] CAI Z.SA-GD：Improved Gradient Descent Learning Strategy with Simulated Annealing[J].arXiv preprint arXiv：2107.07558，2021.

[11] AL-TASHI Q，KADIR S J A，RAIS H M，et al.Binary optimization using hybrid grey wolf optimization for feature selection[J].Ieee Access，2019（7）：39496-39508.

[12] AYDILEK I B.A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems[J].Applied Soft Computing，2018，66：232-249.

（收稿日期：2023-02-17，修回日期：2023-03-22）