油浸式变压器导油板对油流特性与温度分布的影响

刘锐 赵振喜 郑存龙 高峰 刘欣 吴龙飞

基金项目：国网吉林省电力有限公司智慧变电站建设关键技术科技基金（批准号：522371210003）资助的课题。

作者简介：刘锐（1989-），工程师，从事电力工程技术的研究，liurui1@sgepri.sgcc.com.cn。

引用本文：刘锐，赵振喜，郑存龙，等.油浸式变压器导油板对油流特性与温度分布的影响[J].化工自动化及仪表，2023，50（6）：000-000.

DOI：10.20030/j.cnki.1000-3932.202306000

摘  要  變压器的绕组和绝缘油之间散热不均导致绕组局部热点温度过高，影响绝缘材料的绝缘特性。为研究油道和导油板对变压器油的流速、流向以及热点温度的影响，首先对变压器流体域、固体域以及流-固交界面上的传热模型进行分析，确定了流-固界面的传热数学模型。基于此，构建并求解了油浸式变压器数值仿真模型，利用变压器温升试验结果验证了数值模型的准确性。最后，在数值模型中研究了两种横向导油板对变压器油的流场和温度分布的影响。研究表明：基于流-固耦合特性构建的数值模型偏差小于1 ℃，横向挡油板使水平油流平均油速和峰值流速分别提高1.4倍和2.3倍，提高了流-固耦合区域的换热效率，绕组平均温度和热点温度下降3 ℃以上，为变压器绕组散热分析与结构设计提供了新方法。

关键词  油浸式变压器  油流速度  油流方向  温度分布  导油板

中图分类号  TK311          文献标志码  A          文章编号  1000-3932（2023）06-0000-00

油浸式变压器是电力系统中长距离输电的重要设备，其装机数量和容量等级不断上升，安全性和可靠性标准也越来越高[1～3]。变压器电气可靠性最大的隐患是内部绝缘材料性能退化。热点温度超过该处绝缘材料所能允许的长期平均温度则会导致绝缘材料使用寿命减短[4～7]，GB/T 1094.7—2008中对油浸式变压器所使用的绝缘材料老化程度进行了指导，变压器内A级绝缘材料在老化过程中满足六度法则[8，9]。油浸式变压器的负载能力主要由绕组热点温度决定，更进一步地，与变压器损耗产生热量的能力和变压器油的散热能力有关[10，11]。变压器主体浸入变压器油中，绕组油道结构和油流状态对变压器整体的温度分布起决定性作用[12～14]。因此，研究变压器绕组中水平油道的油流速度和方向，分析油流状态对绕组温度分布的影响，可为研发和生产油浸式变压器，减小绕组最热点温度，保护变压器的绝缘性能提供理论依据。

刘畅等基于有限元法，结合绕组区域流固耦合模型，在不同高度位置设置散热器，分析了不同进口油速下变压器热点温度的差异，并在变压器内部搭建光纤传感系统，直接获取绕组温度分布，验证了模型的有效性[15]。王路伽考虑绝缘油运动阻力、多结构耦合传热的变压器热学-流场模型，得到了暂态模型的油指数、绕组指数解析解，由此可计算出绕组的温度分布和顶层变压器油温[16]。金能思等基于热电类比理论的油浸式变压器内部绕组与油之间热行为计算模型，分析油浸式变压器绕组线饼间水平油道的油流状态，得出更具优势的热点温度的组成关系[17]。谷长健等基于热电类比法和传热理论，利用试验方法获取变压器绕组饼间热阻，代入建立的变压器绕组分布式参数热路模型，分析变压器绕组热点温度及其位置[18]。LUO H W等综合考虑变压器布置环境、太阳辐射及空气流动等环境因素以及工作状态的变压器热模型，得到了计算变压器热区域温度和顶部油温度的解析解过程，计算了不同运行状态下变压器的温度分布，并实测了变压器内部温度，验证了模型的准确性[19]。苑翼飞等首先研究了油浸状态绝缘纸的热阻特性随温度的关系，分析了绝缘纸-油耦合界面的传热特性，然后在变压器空间热路模型中引入绝缘纸的热阻和界面换热阻力，构建了更为精确的变压器计算模型，获得了变压器温度分布[20，21]。ZHAO S C等提出一种简化的计算流体动力学模型，将固体-流体耦合面流体流动状态设置为优化过的对流换热计算式，将该模型在变压器散热器上进行了应用研究，优化了变压器散热结构，有效降低了绕组温度[22]。对变压器散热结构的优化研究取得了较大进展，但变压器涉及两相介质耦合散热，加之变压器绕组结构复杂，冷却油流动状态动态变化，对变压器散热研究还处在不断探索阶段。

笔者以SZ11-10000/35型三相双绕组油浸式电力变压器为研究对象，通过分析该变压器产热和散热过程中固体域、流体域及流固耦合等区域的热量传递机理，结合变压器实际结构尺寸及材料物理属性，应用数值分析软件对变压器箱体内主要部件建立三维多相介质耦合计算模型，得到绕组的油流速度和方向，以及固体域、流体域温度场，并将耦合模型的数值计算结果与绕组温升试验温度场进行比较，验证数值计算模型的精度。最后，基于变压器实际强化散热措施，在仿真模型水平油道中构建了两种导油板结构，探究绕组油道内油流速度、方向特征及绕组温度分布。

1  变压器热传递分析

1.1  变压器的热传递

在变压器的工作过程中，由于空载、负载损耗产生大量的焦耳热，高温导致变压器温度升高到内部绝缘材料的最高耐热值，总损耗PT计算式为[23]：

（1）

等式右边前两项和为铜损，I1Nφ、I2Nφ分别是变压器输入侧和输出侧绕组的相额定电流，A；r1，75 ℃、r2，75 ℃分别为75 ℃时变压器输入侧和输出侧绕组总电阻，Ω。等式右边第3项为铁芯等材料产生的磁滞损失，γ为铁芯材料的磁滞系数，Bmax为磁通密度的最大值，T，V为铁芯体积，f为频率，Hz。等式右边第4项为涡流损耗，δ为硅钢片厚度，m。

变压器运行时，其结构件空载和负载损耗产生的热量使冷却油温度升高，由于浮升力和自重力的作用，绝缘油在发热部件和冷却箱之间循环。冷却油将热量带到油箱壁和散热器上，再通过热辐射、对流换热方式与环境交换热量，过程如图1所示。在变压器工作过程中，有效的散热使得系统整体的温升低于温升限值，以保障绝缘材料的绝缘性能、系统的安全性并延长内部绝缘材料的使用寿命。在变压器运行过程中，由于本身产生总损耗的速度有限，同时该热量部分通过变压器油转移到周围介质和环境中，经过一段时间的运行，变压器的温度上升速度变慢，铁芯和绕组的温度将趋于一个相对稳定的状态，在这种状态下，变压器系统的温度场将达到热平衡的状态。

1.2  流固耦合传热数学模型

对于自然油循环变压器，其流动动力是热浮升力和油的重力的合力，比强迫油循环变压器的流动动力小得多，油道里面的冷却油流动较慢。所以，绕组之间的换热能力较差，热量累积，温度过高。变压器箱体内的结构和油的性质对油的流动具有重要影响，既涉及铁芯、盘式绕组等固体结构，又有冷却油这种粘性流体，所以计算温度场必须多方面考虑，其中流-固耦合热分析方法能够有效解决多相多种介质耦合问题。将流-固耦合热分析方法用于油浸式变压器温度分布计算中，分析固体域（如铁芯、低压、高压绕组）的传热方法和流体域（如绝缘油）的流动方式，以及它们的交界面上的传热方法，分析温度计算模型中结构相互作用机理。

对模型进行数值求解涉及到材料属性设置。在变压器中，固体域的温度计算需获得变压器铁芯和绕组的温度分布情况。温度场是关于空间和时间的函数，由于笔者只关心穩态情况的温度分布，舍去时间项，在笛卡尔坐标系中，将变压器各结构的温度场表示成：

（2）

固体域内的铁芯、绕组存在温差时，其中的微观粒子进行热运动，表现为热传导现象，流经固体界面的热流密度与该材料的热传导系数、热流流向上的温度变化率成正比，且热流流向与温度升高的方向相反，变压器固体域的热流密度满足傅里叶定律[24]：

（3）

其中，q为固体域内传热截面上的热流密度，W/m2；λ为热传导系数；n为该点等温线上的法向单位矢量。

在笛卡尔空间坐标系下，固体域热传导的控制方程可写成如下微分方程的形式[25]：

（4）

其中，等式左边为固体域热力学能的增量；等式右边第1项为固体域与相邻固体域之间的热量交换，第2项为固体域内热源生成热；c为铁芯或紫铜绕组等固体域的比热容，J/（kg·K）；ρs为固体域密度，kg/m3；Sh为固体域的内热源，W。

变压器中油流状况可以通过基本的流动控制方程计算，传热过程满足热工三大守恒方程，即假想的微元体与外界交换的热量和自身存储的热量守恒，微元体的质量收支守恒，微元体动量和其他机械能的转换守恒。绝缘油可以看作是常物性、不可压缩的粘性流体，在构建油流数值计算模型时，可以做简化假设，从而得到变压器流体计算模型的简化数学描述。

铁芯、绕组和冷却油的交界面即变压器固体域与流体域的交界面。分析交界面之间的流-固耦合热特性必须计算各部件热量传递关系。已知交界面热量传递前提是流体域和固体域之间存在温差，换热形式可由牛顿冷却定律描述：

（5）

其中，α为流-固交界面上的表面传热系数；ΔT为交界面冷却油温度Tf与固体表面温度Tw的差。

实际上，式（5）只是一个定义式，搭建变压器流-固耦合热模型必须清楚换热具体机理，在ANSYS软件中设置绕组、铁芯等部件与油的耦合面计算参数，以及油箱壁与空气的对流换热系数，其关键参数计算方法如下[26]：

（6）

（7）

（8）

其中，Nu为努塞尔数，Pr为普朗特数，Ral为瑞利数，由这3个无量纲数即可求出油箱壁与空气的对流换热系数α；L为油箱壁的特征尺寸，m；g为重力加速度，m/s2；β为流体的体胀系数，绝缘油视为不可压缩流体；T∞为流体温度；v为流体的动力黏度，kg/（m·s）；k为变压器油的热扩散率，m2/s。

1.3  流-固耦合传热的数值计算方法

在ANSYS的CFX模块中构建包含铁芯、绕组和冷却油的油浸式变压器传热数值计算模型。有限元通过数学上的近似方法，被简化为一个与现实物理系统无限近似的离散情况。有限体积法是由3个守恒方程的一般形式产生的离散方程，守恒方程的一般形式表示如下[27]：

（9）

其中，ρ为冷却油的密度；Γ为广义扩散系数；?为通用变量，代表3个方向的速度分量u、v、w及温度T；S为广义源项。

在控制体内构建控制方程，并通过有限元进行积分求解，得出：

（10）

控制体中构建的连续微分方程表达为离散形式，得到离散方程。通过对离散方程的求解，可得到流体和固体之间耦合传热的解，求解流程如图2所示。

2  变压器流-固耦合模型的建立

2.1  绕组温度模型

变压器油的比热大，是较为理想的冷却剂，将铁芯、绕组及其他结构件产生的热量传递到箱壁外的散热器，随后利用空气的自然对流将热量带走。笔者以云南某公司生产的35 kV/10 000 kVA式变压器为研究对象。变压器为心式结构，铁芯柱半径为220 mm，低压绕组内外径分别为234 mm和290 mm，高压绕组内外径分别为304 mm和364 mm。变压器出厂的温升试验中，施加的空载损耗为9 670 W，施加的负载损耗为55 398 W。应用ANSYS软件的温度仿真模块建立铁芯、绕组温度场的计算模型。根据该变压器的实际材料参数和结构尺寸搭建模型。表1为变压器材料的热物理参数。

在仿真软件ANSYS CFX构建变压器流-固耦合模型时，需在铁芯和绕组部件中设置单位体积热源q，计算方法如下：

（11）

其中，P为铁芯或绕组的产热功率，即温升试验中施加的损耗，W；V为铁芯和绕组的体积，m3。

根据表1中参数计算，可得出铁芯单位热损为1 074 W/m3，加载在高压绕组、低压绕组上的单位热损耗为30 875 W/m3。将各发热源的热损转换为体载荷，各单位体积热损耗离散化为各离散固体域的热源。

2.2  变压器物理模型

变压器内部的三相绕组呈对称排列，且单个绕组近似为同心圆环结构，结构一致性较好，因此取一相绕组进行模型计算。根据绕组材料参数，建立油浸式变压器单相绕组的3维模型。将铁芯和绕组简化成圆柱体，每饼之间的油道高度为2 mm，绕组总高度为520.5 mm。对模型简化如下：

a. 环境温度恒为室温，流速恒定；

b. 固体域均匀发热；

c. 忽略相邻绕组间的互感影响。

根据变压器油箱的实际尺寸设置油流区域对油道中的油流进行计算，如图3所示。

本研究通过求解控制方程，对图3所示的流体、固体计算区域进行网格划分，将添加流油的连续微分方程离散化，再对方程进行求解。采用CFX软件进行计算，在计算区域上得到解。网格划分是将物理坐标中的基本方程转化为可计算的均匀网格，网格划分的质量关系到模型仿真的速度与准确度。笔者采用软件自动划分网格类型为非结构化的四面体，总网格数为1 258 390，平均网格质量为0.702，满足数值计算的要求。

对于自然油循环变压器，变压器油的流动力主要受温度变化的影响，为油密度降低后向上流动的热浮升力和油密度升高后向下流動的重力。求解流体力学结果前需对模型的边界条件和初始条件进行设置，具体如下：

a. 载荷。变压器铁芯、绕组等固体域为热源，损耗与体积的比值即单位体积固体域热生成量，将损耗转换为体载荷。

b. 流动型态。通过临界雷诺数确定流体的流动模式，分为层流和湍流两种。在软件中选择层流可通过非稳态N-S方程对油流进行控制。

c. 流体模型。变压器油流流速低，将流体模型设定为低流速体的焓分布数学模型，仅对固液传热进行求解，忽略油流动能产生的热量变化。

d. 耦合边界条件。对油流与绕组、铁芯的接触面设置流-固耦合边界条件，变压器油箱壁和外界空气的传热系数设置为5 W/（m2?K），辐射系数设置为0.9。

e. 全场的压力设置。压力设置为标准大气压，将所有的压力与标准大气压作比较，以此来提高精度。

3  流-固耦合传热仿真计算结果及水平油道导向结构

3.1  绕组温升及试验对比分析

利用流-固耦合传热模型对变压器的油流及温升进行求解计算。图4a为变压器单相绕组三维模型的温度分布计算结果，图4b为高压绕组和低压绕组三维模型温度分布细节图。

由图4可以看出，通过变压器绕组三维模型计算的高压绕组和低压绕组温度场基本一致，表明简化等效的流-固耦合热模型精度较高。从绕组温度分布来看，整个变压器热点温度为339.9 K。因为变压器绕组涡流损耗，高压绕组和低压绕组的热点温度位于绕组顶部区域。还因为低压绕组靠近铁芯热源，且散热空间较小，而高压绕组外侧为大空间散热，低压绕组热点温度和平均温度均高于高压绕组相应的温度值。另外，低压绕组最低温度约为327 K，高压绕组最低温度约为324 K，均位于绕组中下部位置。绕组底部温度值高于中部绕组温度，由底部铁芯的涡流损耗造成。

为考察变压器流-固耦合热模型数值计算精度，搭建变压器温度测量试验平台测量绕组温升。温度传感器采用了实验室试制的全介质光纤布拉格光栅（Fiber Bragg Grating，FBG）温度传感器，对10支FBG温度传感器进行3次重复测试，其中2只传感器波长与温度的关系曲线以及传感器静态指标如图5所示。试验中，温度传感器嵌入绕组水平油道的垫片内，减小传感器对原温度场影响的同时，能够准确检测到绕组部位的温升。笔者沿高压绕组等间距布设了10只FBG温度传感器，传感器布设照片如图6所示。

对嵌入FBG传感器的变压器实体进行加载试验，达到稳态后获取传感器读数。试验数据表明，随高度升高，绕组温度呈上升趋势，最高温度在绕组上部，由于传感器布设间距，试验数据的最大值不一定是绕组热点温度。在数值模型中取对应高度的温度计算值，试验测得的温度和数值模型计算的温度对比如图7所示。变压器温升试验温度值略高，两者的偏差小于2 K，可以看出流-固耦合数值计算模型具有较好的精度。

3.2  导油板结构对绕组温升的影响分析

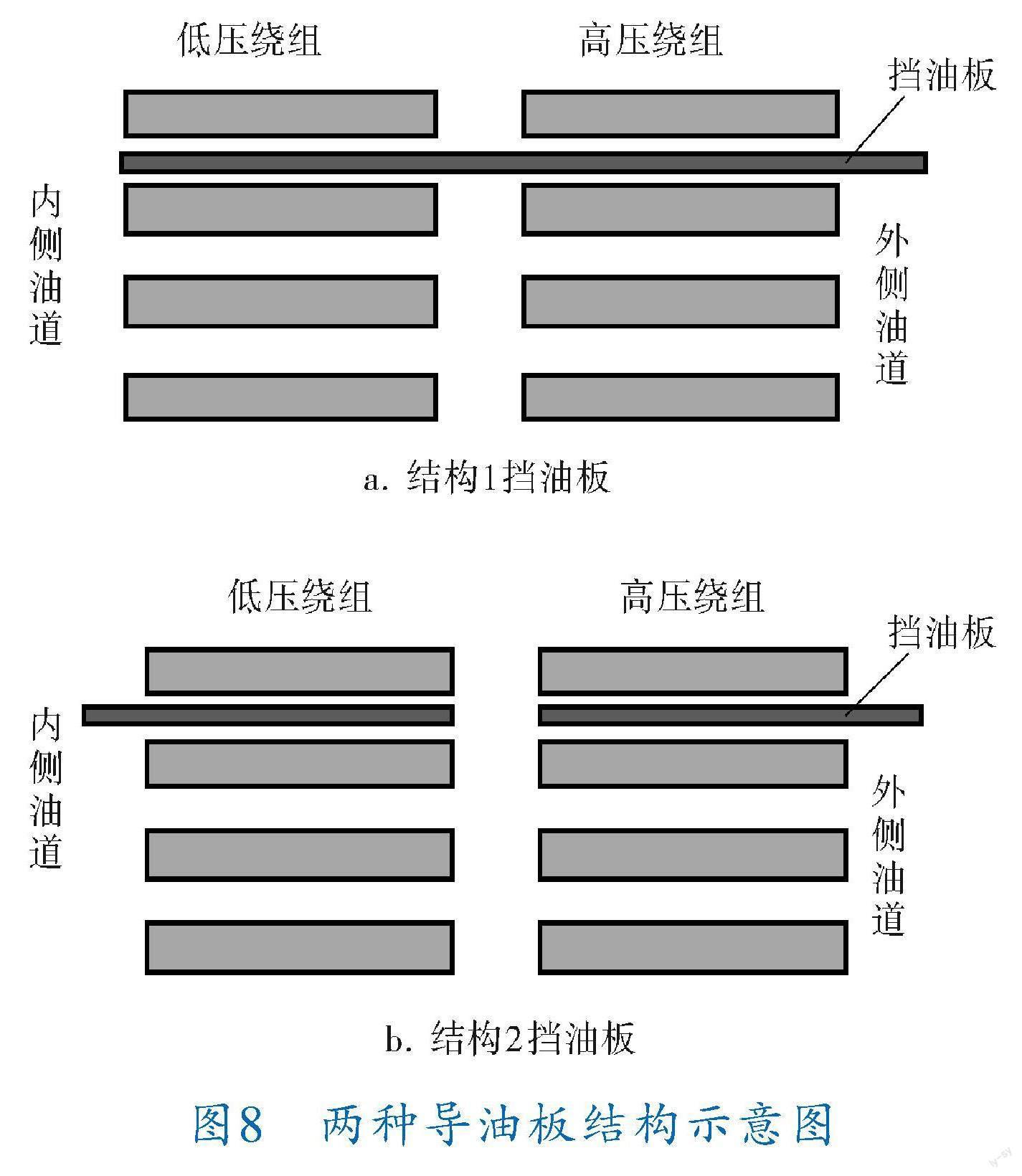
水平油道的变压器油受到阻滞作用会形成死油区，进而影响绕组的散热。通过在饼间加设导向结构的挡油板，改变油道内油流的流向、流速状态以避免死油区的形成。保持流-固耦合热模型中其他结构不变，在第1和第54条水平油道中增加两种形式的1 mm厚的绝缘板挡板，结构如图8所示。

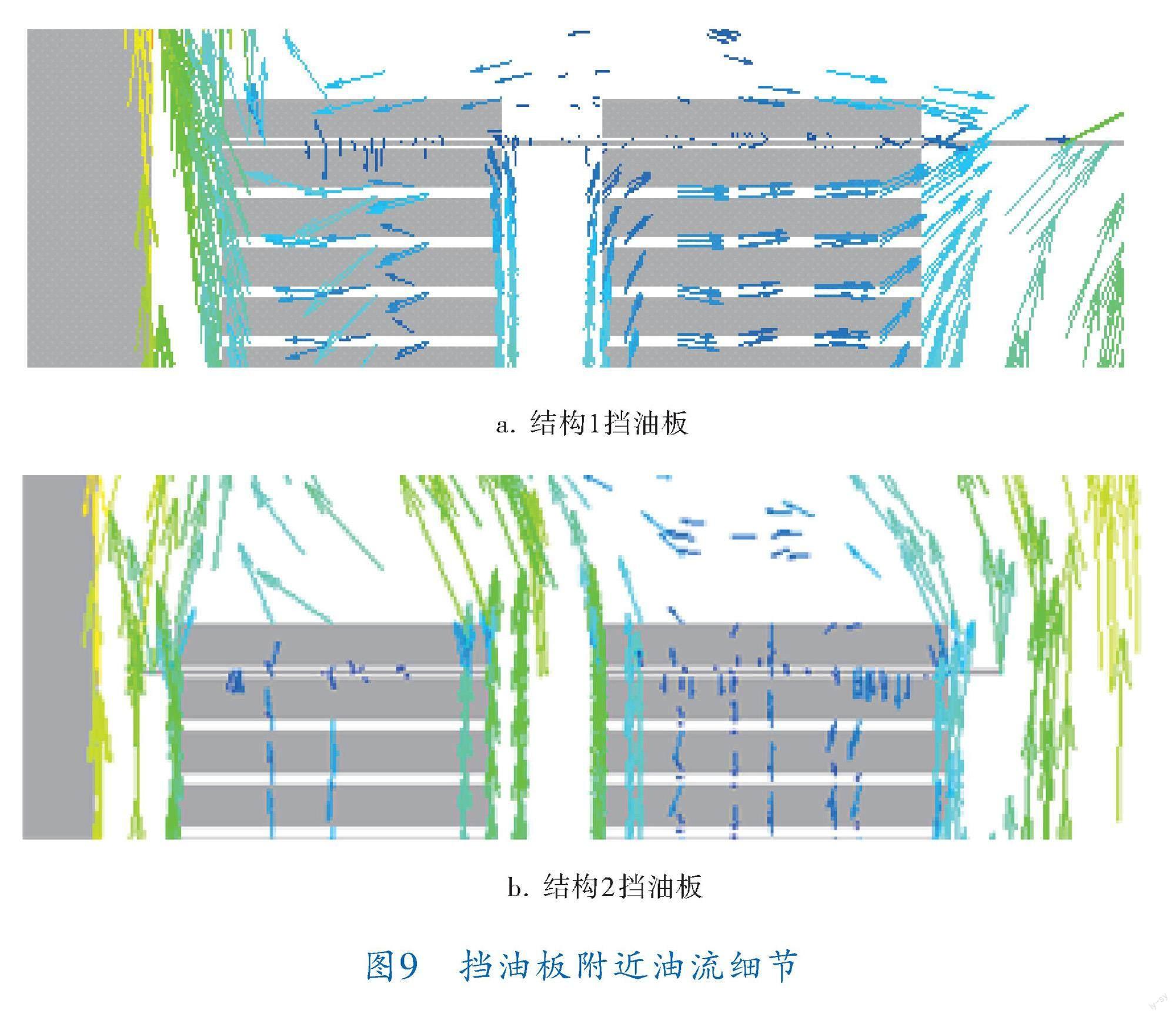
在含有挡板结构的变压器绕组流-固耦合热模型中，设置相同的边界条件和结构参数，对模型进行流-固耦合数值计算。导油板周围和顶层水平油道中的油流方向如图9所示。结构1挡油板呈贯通趋势，阻挡了高低压绕组之间的竖直油道。竖直油流向上流动到达挡板处，转为横向流动，穿透水平油道流出，从两侧的竖直油道向上流动。结构2挡油板阻挡了内外两侧竖直油道部分流通区域，提高了水平油道两侧静压差，促使油流水平流动。可见两种结构不同程度地加快了挡板附近的水平油道油流速度，增强水平油道和竖直油道油流的流动性。

图10展示了无挡板结构和两种不同挡板结构模型的油流分布情况。其中，不加挡板时水平油道最大流速1.476×10-3 m/s，增加结构1挡油板后，水平油流最大流速提高2.8倍，达到4.204×10-3 m/s，增加结构2挡油板后，最大流速提高2.3倍，达到3.356×10-3 m/s。水平油道平均流速从1.222×10-3 m/s，分别提升1.6倍和1.5倍，有效改善了油道油流。

挡板结构提高了挡板附近竖直油道两端的静压差，加快了水平油道内的流速，促进了绕组与冷却油之间的热流交换。不加挡油板及分别增设两种结构挡油板的绕组温度分布如图11所示。不加挡板结构热油直接向上运动，高温区域集中在绕组顶部。增加两种结构挡油板后，绕组热点温度从341.1 K分别降低到338.4 K和337.3 K，并且绕组热点位置与无导向结构相比有所降低。在3种结构的绕组竖直方向上取10个点，对绕组平均温度分布进行统计对比，结果如图12所示。增加两个不同的挡油板结构后，热点的位置由顶部绕组下降到距绕组顶部10%的位置，绕组整体温升减小，对绕组高温部分的改进非常明显。

4  结束语

为改善油流、降低绕组热点温度、强化绕组的散热能力，以SZ11-10000/35型油浸式变压器为原型，在数值模型中设计了两种不同结构的挡油板，计算出了油流场和温度场。结果表明，基于流-固耦合特性构建的三维数值仿真模型计算结果与传感器检测数据偏差小于1 ℃，安装的两种挡油板均能改善水平油道中油流的流向与流速，水平油道最大流速由1.476×10-3 m/s分别增加到4.204×10-3 m/s和3.356×10-3 m/s。平均流速由1.222×10-3 m/s分别提升到1.955×10-3 m/s和1.833×10-3 m/s，有效改善了油道油流速度，提高了流-固耦合区域的热交换效率，绕组的平均温度和最热点温度分别下降3 ℃以上，有利于延缓变压器内部绝缘材料的老化，增加变压器的使用寿命。

参  考  文  献

［1］郭庆奎.变压器油中气体常规故障诊断方法的探讨与展望[J].化工自动化及仪表，2017，44（9）：818-822.

［2］杨超，程新功，陈芳，等.油浸式电力变压器热路模型研究综述[J].电工电气，2018（8）：1-6；45.

［3］LAN J，KIM D，ABU-SIADA A，et al.Oil-Immersed Power Transformer Condition Monitoring Methodologies：A Review[J].Energies，2022，15（9）：3379.

［4］ZHANG M Z，LIU J，LIAO L L，et al.Method for predicting the remaining life of oil–paper insulation system based on stochastic degradation process[J].IET Science， Measurement & Technology，2019，13（4）：478-485.

［5］LIU J，LV J L，ZHANG M Z，et al.Research on Life Prediction of Oil-Paper Insulation Based on Dielectric Response[J].Electric Power Components and Systems，2020，48（3）：281-290.

［6］何先华，张远鹏，崔桂兴，等.基于回归算法的变压器故障检测方法研究[J].电力系统保护与控制，2020，48（21）：132-139.

［7］ZHANG E Z，LIU J，ZHANG C H，et al.State-of-Art Review on Chemical Indicators for Monitoring the Aging Status of Oil-Immersed Transformer Paper Insulation[J].Energies，2023，16（3）：1396.

［8］中华人民共和国国家质量监督检验检疫总局.电力变压器  第7部分：油浸式电力变压器负载导则：GB/T 1094.7—2008[S].北京：中国质检出版社，2009.

［9］郑一鸣，何文林，孙翔，等.基于油色谱超立方映射的电力变压器缺陷援例诊断模型[J].电力工程技术，2017，36（4）：48-53.

［10］赵莉华，王释颖.油浸式变压器高温绝缘材料的研究现状[J].绝缘材料，2016，49（4）：1-6.

［11］周晨，高强，刘海.基于变压器和负荷需求响应协调的配电网实时电压控制策略[J].电力电容器与无功补偿，2021，42（6）：143-150.

［12］肖强，王红艳，陈晴，等.油浸式电力变压器内部温度场与流场特性分析[J].南京工程学院学报（自然科学版），2016，14（1）：60-64.

［13］陈伟根，李孟励，孙才新，等.变压器绕组热点温度热电类比计算模型仿真分析[J].重庆大学学报，2010，33（12）：8-13.

［14］陈忠贤，谢虎波，任文军，等.基于FBG的35 kV油浸式变压器绕组变形监测研究[J].智慧电力，2023，51（1）：115-122.

［15］刘畅，赵振刚，黄嘉，等.油浸式变压器进口油速对绕组热点温度的影响[J].昆明理工大学学报（自然科学版），2020，45（4）：85-90.

［16］王路伽.高速鐵路牵引变压器温升建模及应用研究[D].成都：西南交通大学，2020.

［17］金能思，许晓平，文贺敏，等.基于热电类比理论的油浸式变压器绕组热行为计算模型[J].化工自动化及仪表，2019，46（9）：725-730.

［18］谷长健，文贺敏，万小容，等.油浸式变压器绕组分布式参数热路模型研究[J].化工自动化及仪表，2019，46（9）：736-740；775.

［19］LUO H W，CHEN L K，JIANG G Y，et al.Thermal Circuit Model of the Transformer Considering Environment Factors and Its Application[J].High Voltage Engineering，2018，44（11）：3561-3568.

［20］苑翼飛，赵振刚，罗川，等.油浸式变压器绝缘纸热阻的温度特性[J].高电压技术，2019，45（6）：1754-1761.

［21］LUO C，ZHAO Z G，ZHANG D C，et al.Temperature effect on the thermal properties of insulation paper[J].Electrical Engineering，2021，103：1083-1091.

［22］ZHAO S C，LIU Q，MARK W，et al.A Reduced Radiator Model for Simplification of ONAN Transformer CFD Simulation[J].IEEE Transactions on Power Delivery，2022，37（5）：4007-4018.

［23］潘文霞，陈星池，赵坤等.基于温度场计算的油浸式变压器热点温度仿真分析方法[J/OL].电测与仪表：1-8[2023-07-18].http：//kns.cnki.net/kcms/detail/23.1202.TH.20221019.1050.006.html.

［24］马玉龙，王永庆，朱超，等.大型油浸式变压器内部及热点的数值计算与温度研究[J].工业加热，2020，49（2）：50-55.

［25］刘国坚，王丰华.油浸式电力变压器温度场分布的计算分析[J].科学技术与工程，2015，15（32）：36-41.

［26］CHEN Y，LUO C，XU W J，et al.Study on Oil Flow Characteristics and Winding Temperature Distribution of Oil-immersed Transformer[J].Distributed Generation & Alternative Energy Journal，2021，35（3）：173-194.

［27］金能思.油浸式变压器分布参数热路模型边界条件研究[D].昆明：昆明理工大学，2020.

（收稿日期：2023-05-05，修回日期：2023-07-29）