一种最速控制器的机理研究与应用

陈锦攀 赵兵 孙闻 罗滇生 梁爽 廖峰 王伟 梁晓兵 王玲 李德波

基金项目：国家自然科学基金重点项目（批准号：51376161）资助的课题；中国南方电网有限责任公司科技项目（批准号：GDKJXM20222593）资助的课题；中国南方电网有限责任公司科技项目（批准号：GDKJXM20210174）资助的课题。

作者简介：陈锦攀（1985-），高级工程师，从事最速控制机理研究及工程最速控制技术专利布局方面的工作，xu_19pan@163.com。

引用本文：陈锦攀，赵兵，孙闻，等.一种最速控制器的机理研究与应用[J].化工自动化及仪表，2023，50（6）：000-000.

DOI：10.20030/j.cnki.1000-3932.202306000

摘  要  随着我国“双碳”能源目标的提出，传统PID控制已经很难适应现有火电机组的控制。因此，提出加速型工程最速比例-积分（AEFPI）控制器，显著提高了反馈控制性能。文章首次揭示AEFPI机理，通过仿真实验和数学计算分析AEFPI控制特性，给出AEFPI在提高反馈控制性能上实质性进步的理论依据。最后，通过难控过程的实际应用进一步验证了AEFPI的先进性。

关键词  加速型工程最速比例-积分控制器  直角三角窗函数滤波  加速型工程最速跟踪滤波器  频域滤波特性

中图分类号  TP273      文献标志码  B      文章编号  1000-3932（2023）06-0000-00

回顾工控技术的发展历程，为了适应工业动力发展的需求，1788年瓦特借助飞锤调节器实现了蒸汽机转速控制，奠定了工控基本原理，即反馈控制原理（又称瓦特原理）[1]，飞锤调节器实现了一种比例作用的反馈控制，比例作用的反馈控制的明显问题是存在系统稳态偏差，但那个时代的工业动力系统，对转速控制的精度要求并不高。电机工程[2]发展对控制提出了较高的需求，1936年CAL-LENDER A和STEVENSON A发明比例-积分-微分（Proportional-Integral-Derivative，PID）控制器[3～7]，实现了系统稳态偏差为零的控制。PID控制器的范畴包括比例-积分（PI）控制器，在20世纪40年代形成了以NYQUIST H提出的奈氏稳定判据[8]、伯德建立的反馈控制系统频域分析工具（即伯德图）[9]、EVANS W R提出的根軌迹法[10]等为核心的经典控制论[11]，推动了PID控制技术在工控领域的广泛应用。20世纪50年代末，为适应航空航天领域发展要求，形成了以原苏联科学家PONTRYAGIN提出的极大值原理[12]、美国学者BELLMAN创立的动态规划[13]、KALMAN建立的卡尔曼滤波理论[14]等为基础的现代控制论[11]。经过半个多世纪的发展，产生出宏大和严密的现代控制论和众多的先进控制策略[15～23]，先进控制的本质是一种“建模-优化”策略，即以数学模型[11]为基础、以最优控制[11]为核心。

在工控领域，PID至今占据着统治地位[24]，这其实也是一种无奈的选择[25]。随着我国“双碳”能源目标的提出，风力发电、光伏发电发展形势迅猛，电网调节压力巨大，目前的主要调节手段就是大幅提升现有燃煤火电机组[25]深度调峰快速调频性能[25]，但从现有火电机组控制的角度，PID控制很难适应。由此，电力系统的工程研究人员发明了一种加速型工程最速跟踪滤波器（Acceleration Engineering Fastest Tracking Filter，AEFTF）[26]，它代表了一种最速跟踪滤波机制，显著提高了输出跟踪输入的效率。采用AEFTF构造出的加速型工程最速比例-积分（Acceleration Engineering Fastest Proportional-Integral，AEFPI）[26]控制器，代表了一种新型工业反馈控制技术，相对于PID、PI，AEFPI在提高反馈控制性能上有实质性进步。现通过数学计算分析AEFPI的控制特性，给出AEFPI在提高反馈控制性能上实质性进步的理论依据，并通过仿真实验和实际应用进一步验证AEFPI的先进性。

文中变量、参数、函数的表达均是唯一的。为了表述简洁，如无特别说明，时间、时间常数的单位是s，加速度的单位是s-2，频率ω的单位是rad/s，相位、相位稳定裕度的单位是（°），比例增益无量纲，阶次无量纲，常用对数20lg的单位为dB。

1  直角三角窗函数滤波

2021年，工程研究人员在火电机组控制实践中，发明了一种加速型最速跟踪滤波器（Acceleration Fastest Tracking Filter，AFTF）[27]，就是在给定时间常数内AFTF输出加速跟踪到输入。

机理上，AFTF是一种直角三角窗（Right Triangle Window，RTW）函数滤波[28]，RTW在目前的窗函数滤波中没有出现过，是一种原始创新。RTW的拉普拉斯函数表达式为：

（1）

其中，fRTW（s）为RTW的传递函数，TW为窗口时间长度。

输入单位阶跃，在TW=10 s得到的RTW过程输出PVRTW（t），如图1所示。

时间t/s

图1  RTW过程输出特性示意图

对RTW进行2倍增益、常数为TW的积分，得到的AFTF传递函数fAFTF（s）计算式为：

（2）

其中，TAFTF为AFTF时间常数。

输入单位阶跃，得到的AFTF输出为：

（3）

其中，PVAFTF（t）为AFTF在单位阶跃信号输入的过程输出，aAFTF为AFTF跟踪输出加速度。

设置TAFTF=10 s，输入单位阶跃信号，获得AFTF的过程输出，如图2所示。

时间t/s

图2  AFTF的过程输出特性示意图

由图2可知，在t≤10 s时，PVAFTF（t）以aAFTF跟踪输入；在t＞10 s，PVAFTF（t）跟踪到输入。

在实践中发现，采用直角三角窗（RTW）函数滤波即AFTF直接构造出的新型反馈控制器，存在累计误差，需要完成AFTF的工程化。

2  加速型最速跟踪滤波器的工程化

文献[26]完成了加速型最速跟踪滤波器AFTF的工程化，得到AEFTF，采用AEFTF构造出的AEFPI有效解决了上述累计误差问题。但文献[26]给出的AFTF工程化方法不够严谨，现对此问题进行修正。

首先将AFTF在单位阶跃输入的过程输出PVAFTF（t）近似为1～n阶纯滞后环节相加，得到的近似AFTF（Approximations Acceleration Fastest Tracking Filter，AAFTF）为：

（4）

其中，fAAFTF（s）为AAFTF的传递函数，τ为纯滞后时间常数，l和i均为自然数。

在AAFTF的基础上，采用1～n阶惯性滤波器替换AAFTF中的1～n阶纯滞后环节，得到AEFTF的传递函数fAEFTF（s）为：

（5）

其中，TAEFTF为AEFTF时间常数。

1～n阶惯性滤波器具有自平衡能力，用于AFTF工程化不存在发散的问题。

从工程的角度，出于实际需要，对AEFTF进行变化是可能的。AEFTF分离为A型滤波器（A Type Filter，ATF）和B型滤波器（B Type Filter，BTF）：

（6）

其中，fATF（s）为ATF的传递函数，fBTF（s）为BTF的传递函数。

输入单位阶跃，在n=16、TAEFTF=10 s，得到的ATF过程输出PVATF（t）和BTF过程输出PVBTF（t）如图3所示。

时间t/s

图3  ATF、BTF的过程输出特性示意图

在n=16、TAEFTF=10 s，得到的ATF幅频增益特性GATF（ω）和BTF幅频增益特性GBTF（ω）如图4所示。

频率ω/rad·s-1

图4  ATF、BTF幅频增益特性示意图

ATF、BTF同属于AEFTF范畴，根据应用角度的不同，AEFTF、ATF、BTF可单独选择。相对而言，ATF高频幅频衰减特性为-20 dB/10倍频程，输出跟踪输入特性较好，适合用于新型反饋控制器构造；BTF高频幅频衰减特性为-40 dB/10倍频程，高频衰减特性较好，适合用于信号滤波。

文献[26]实际上是将ATF用于构造AEFPI，便于传承，如无特别说明，AEFTF均指ATF。

3  滤波器性能仿真比较

现将加速型工程最速跟踪滤波器与FOIF进行性能对比。其中，FOIF的传递函数表达式为：

（7）

其中，TFOIF为FOIF的时间常数。

设置n=16、TAEFTF=TFOIF=10 s，输入单位阶跃信号，得到的AFTF、FOIF、AEFTF过程输出PVAFTF（t）、PVFOIF（t）和PVAEFTF（t）如图5所示。

时间t/s

图5  AFTF、AEFTF、FOIF的过程输出特性示意图

根据图5，在t=10 s得到PVAFTF（t）=1.0、PVAEFTF（t）=0.90、PVFOIF（t）=0.63；在t=22.9 s得到PVFOIF（t）=0.90。

在工程上，n值不可能无限大，取n=16已经能够满足实际需要，文中默认n=16。

输入单位方波，在方波周期为100 s，TAEFTF=TFOIF=10 s，得到的AEFTF和FOIF输出仿真结果如图6所示，可见，相对FOIF，AEFTF输出能够较好地跟踪方波。

时间t/s

图6  输入方波的过程输出特性示意图

得出基本结论1：相对FOIF，AEFTF能够显著提高输出跟踪输入的性能，即显著减小滤波滞后。

文献[26]指出，PID结构是基于FOIF构造的，FOIF代表的是一种典型的指数型跟踪滤波机制。

基于上述性能比较结论，指出AEFTF代表了一种典型的最速型跟踪滤波机制。

4  滤波器频域滤波特性计算

AEFTF、FOIF的频率特性函数表达为：

（8）

其中，FAEFTF（jω）为AEFTF的频域函数，GAEFTF（ω）为AEFTF的幅频增益，PHAEFTF（ω）为AEFTF的相频相位，ω为正弦频率，FFOIF（jω）为FOIF的频域函数，GFOIF（ω）为FOIF的幅频增益，PHFOIF（ω）为FOIF的相频相位。

在TAEFTF=TFOIF，当ω趋于无穷大，则GFOIF（ω）：GAEFTF（ω）=8.5，约18.69 dB。

在TAEFTF=TFOIF=10 s，得到的AEFTF、FOIF的幅频增益和相频相位如图7、8所示。

频率ω/rad·s-1

图7  AEFTF、FOIF幅频增益特性示意图

频率ω/rad·s-1

图8  AEFTF、FIOF相频相位特性示意图

用ω-3dB表示GFOIF（ω）、GAEFTF（ω）衰减到-3 dB的频率带宽，用ω-20dB表示GFOIF（ω）、GAEFTF（ω）衰减到-20 dB的频率带宽，用ω-20dB：ω-3dB表示FOIF、AEFTF滤波RC。根据表1，AEFTF在-3 dB增益的频率带宽为FOIF的2.707倍，AEFTF的RC数值明显小于FOIF，即AEFTF与理想滤波的接近程度明显高于FOIF。在ω＞0.658 rad/s，AEFTF的幅频增益衰减特性明显高于FOIF，其中，在ω＞3 rad/s时，GFOIF（ω）：GAEFTF（ω）＞18 dB。在ω＜1.28 rad/s时，GAEFTF（ω）、PHAEFTF（ω）呈单调变化。

表1  FOIF、AEFTF滤波矩形系数

滤波器

ω-3dB

ω-20dB

RC

FOIF

0.100 0

0.994 9

9.949

AEFTF

0.270 7

0.658 4

2.432

AEFTF的重要特性还表现在：AEFTF的高频幅频衰减特性为-20 dB/10倍频程，高频相位趋于-90°，因此AEFTF的高频特性趋于一阶。

得出基本结论2：AEFTF的频域滤波特性显著优于FOIF。

AEFTF有多种重要用途，具体如下：

a. AEFTF的基本用途是过程信号的去噪滤波[25]，相对FOIF，AEFTF显著提高了输出跟踪输入的性能，即减小了滤波滞后。

b. 文献[29]用AEFTF构造了一种加速型工程最速跟踪微分器（Acceleration Engineering Fastest Tracking Differentiator，AEFTD），能够显著提高跟踪微分的性能。

c. 文献[26]用AEFTF构造了一种加速型工程最速积分器（Acceleration Engineering Fastest Integrator，AEFI），显著提高了跟踪常值扰动的效率。

d. AEFTF的高频特性趋于一阶是一个有价值的特性，将AEFTF反转，用于构造新型超前观测器（Novel Ahead Observer，NAO），在NAO输出降阶或滤波处理上相对简单。

5  加速型工程最速比例-积分控制器与最优比例-积分控制器的性能比较

5.1  控制器结构

PI控制器属于PID的范畴，在控制工程实践中，大量运用的是PI控制器，原因是PI控制器仅有2个参数，用法更简单。PI结构基于FOIF构造，出于对比的需要，采用串级PI结构。在串级PI结构基础上，采用AEFTF取代FOIF，得到AEFPI。其中，PI结构如图9所示，AEFPI结构如图10所示。

图9  PI控制器结构示意图

图10  AEFPI结构示意图

PI控制器表达为：

（9）

其中，fPI（s）为PI的传递函数，KP为串级比例增益，TI为积分时间常数。

AEFPI表达为：

（10）

其中，fAEFPI（s）为AEFPI的传递函数，KAEFPI串级比例增益，fAEFI（s）为AEFI的传递函数，TAEFI为AEFI的时间常数。

5.2  性能计算

衡量AEFI的性能需要有参考对象，在积分常数相同时，采用AEFI与CI的相对零频率增益（Relative Zero Frequency Gain，RZFG）来衡量AEFI跟踪常值的效率。CI、AEFI频域函数为：

（11）

其中，FAEFI（jω）为AEFI的频域函数，FCI（jω）为CI的频域函数。

当ω趋于0时，AEFI的频域函数为：

（12）

其中，RZFGAEFI：CI为AEFI相对CI的RZFG。

根据式（12），在TAEFI=TI，当ω趋于0，AEFI的零頻率增益是CI的1.4545倍。

出于对比的目的，定义仿真控制系统（Simulate Control System，SCS），如图11所示，其中，反馈控制器（Feedback Controller，FC）具体为PI、AEFPI，外扰通过耦合模型（Coupling Model，CM）直接耦合到控制过程（Control Process，CP）的输出端即过程输出中。外扰采用斜坡函数（Ramp Function，RF），RF速率为1 000 s，RF长度为2 000 s。

图11  仿真控制系统示意图

定义CP和CM为：

（13）

其中，fCP（s）为CP的传递函数，fCM（s）为CM的传递函数。

PI、AEFPI开环系统（Open Loop System，OLS）的频域函数为：

（14）

其中，FAEFPI：OLS（jω）为AEFPI开环系统频域函数，FAEFPI（jω）为AEFPI的频域函数，FCP（jω）为CP的频域函数，GAEFPI：OLS（ω）、PHAEFPI：OLS（ω）为AEFPI开环系统幅频增益、相频相位，PMAEFPI：OLS为AEFPI开环系统的相位稳定裕度，AMAEFPI：OLS为AEFPI开环系统的幅值稳定裕度；FPI：OLS（jω）为PI开环系统频域函数，FPI（jω）为PI的频域函数，GPI：OLS（ω）、PHPI：OLS（ω）为PI开环系统幅频增益、相频相位，PMPI：OLS为PI开环系统的相位稳定裕度，AMPI：OLS为PI开环系统的幅值稳定裕度。

在临界稳定，即PMAEFPI：OLS=PMPI：OLS=0°、AMAEFPI：OLS=AMPI：OLS=0 dB时，得到的AEFPI、PI临界稳定参数搜索结果如图12所示。

图12  AEFPI、PI临界稳定参数搜索结果

根据图12，在KP=1.736，得到TI：KP最低值为50.17 s，所对应的参数为PI最高性能参数，即KP=1.736、TI=87.1s，简称为A组PI参数；在KAEFPI=4.913，得到TAEFI：KAEFPI最低值为44.18 s，所对应的参数为AEFPI最高性能参数，即KAEFPI=4.913、TAEFI=217.1 s，简称为A组AEFPI参数。

根据A组PI参数、A组AEFPI参数，得到的GPI：OLS（ω）、GAEFPI：OLS（ω）特性如图13所示。

频率ω/rad·s-1

图13  AEFPI、PI开环系统幅频特性示意图

A组AEFPI参数、A组PI参数代表了AEFPI、PI的最高反馈控制性能，已经无法再超越了。根据图13，在给出的ω范围，GAEFPI：OLS（ω）高出GPI：OLS（ω）至少3.73 dB以上（即1.53倍以上），这是AEFPI相对PI能够显著提高反馈控制性能的理论依据。

实际控制系统需要有一定的稳定裕度，笔者将开环系统幅频增益、相频相位用于获取AEFPI、PI参数，给出的参数搜索条件是：对AEFPI、PI参数，在PHAEFPI：OLS（ω）=-135°时满足GAEFPI：OLS（ω）=0.5、在

PHPI：OLS（ω）=-135°时满足时GPI：OLS（ω）=0.5，如图14所示。这种参数搜优点在于拥有良好的鲁棒性，如在控制过程失配，以及控制过程增益增加2倍情况下，仍然能保证开环系统相位稳定裕度在45°。

频率ω/rad·s-1

图14  参数搜索条件示意图

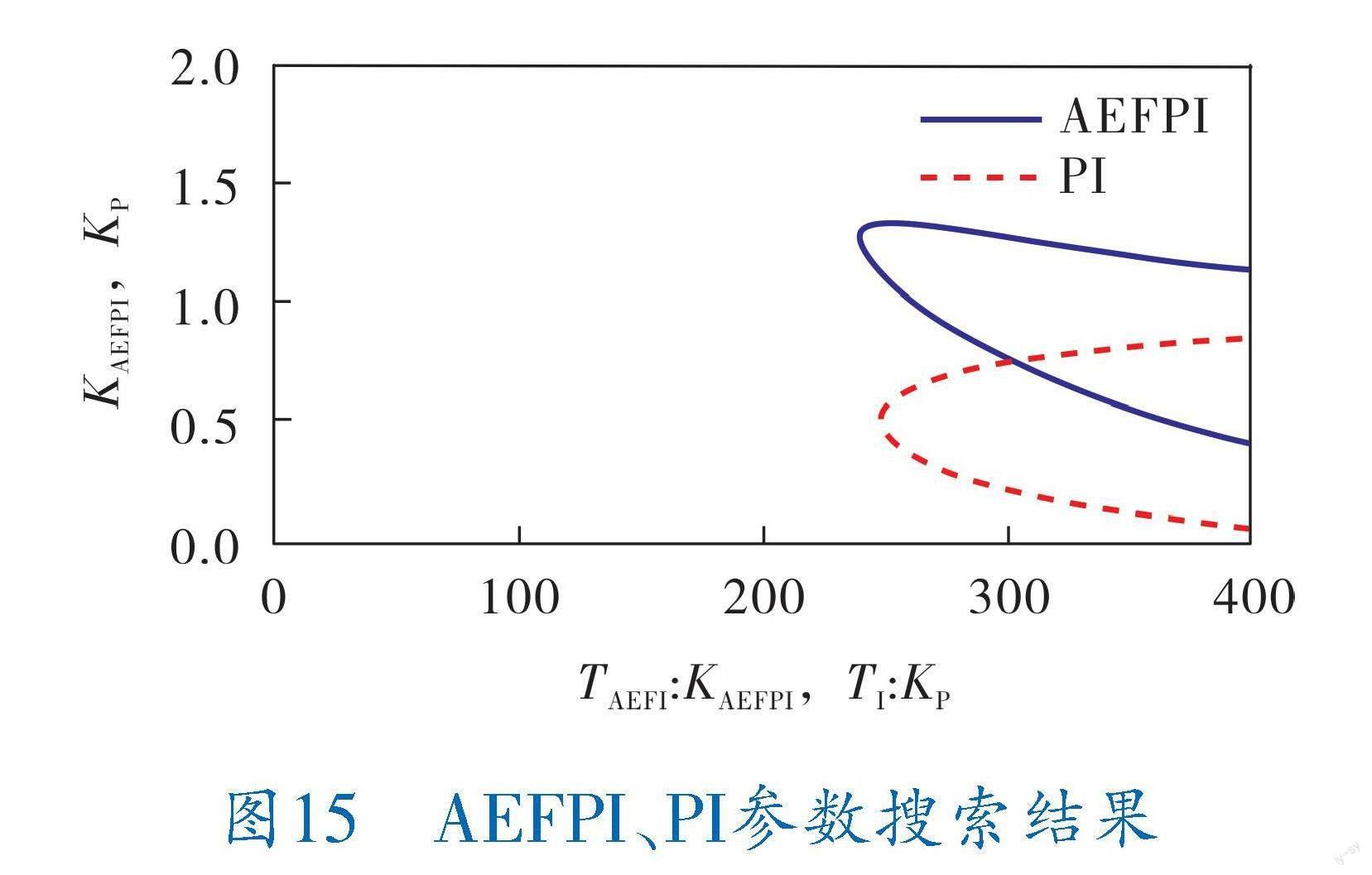
根据图14，得到的AEFPI、PI参数搜索结果如图15所示。

图15  AEFPI、PI參数搜索结果

根据图15，在KP=0.535，得到TI：KP最低值为248.78 s，得到B组PI参数为KP=0.535、TI=133.1s；在KAEFPI=1.296，得到TAEFI：KAEFPI最低值为241.58 s，得到B组AEFPI参数为KAEFPI=1.296、TAEFI=313.1s。

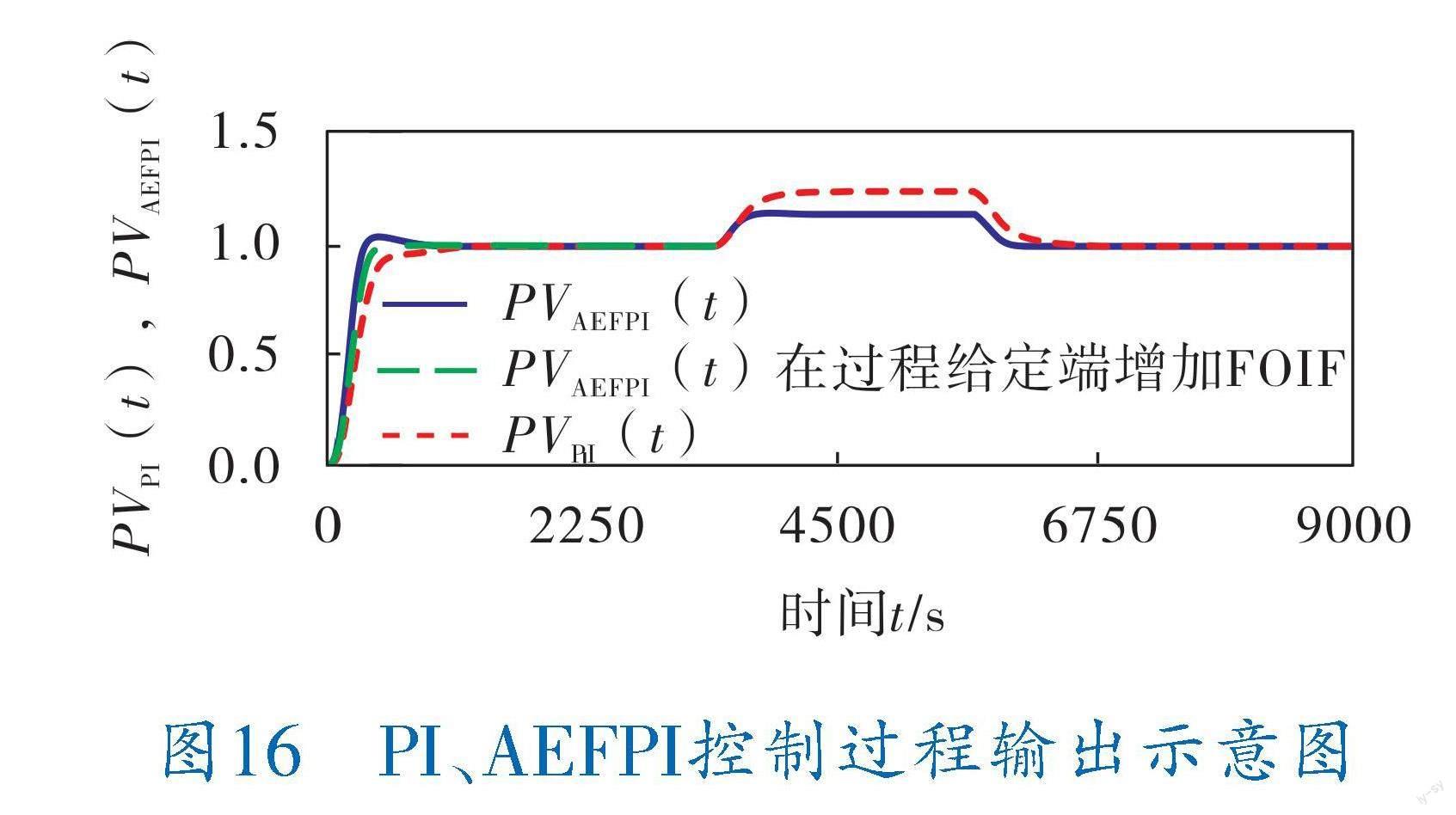
将B组PI参数、B组AEFPI参数用于仿真，过程给定为单位阶跃，在t＞3000 s加入RF，得到的PI控制的过程输出PVPI（t）、AEFPI控制的过程输出PVAEFPI（t）的仿真结果如图16所示。

时间t/s

图16  PI、AEFP控制过程输出示意图

根据图16，得到的AEFPI、PI控制主要性能指标见表2（在工程上，调节时间是指过程进入到小于5%偏差的时间）。

表2  AEFPI、PI控制的主要性能指标

控制方法

第1峰值

第2峰值

过程超调

调节时间/s

PI

1.000

1.0

0.000

501

AEFPI

1.049

1.0

0.049

264

AEFPI控制过程略有超调，因为比例控制量大于1，即KAEFPI=1.296。AEFPI控制过程略有超调是AEFPI固有特性决定的。某些系统不允许出现超调，在过程给定端增加一个FOIF即可解决超调问题。其中，在TFOIF=100 s得到的仿真结果如图16所示。

需要指出，对于恒值控制（即设定值固定），过程超调没有意义，在火电机组过程控制中，有约占70%的控制回路属于恒值控制。

根据图16，得到的AEFPI和PI抑制外扰主要性能指标见表3。

表3  AEFPI、PI抑制外扰的主要性能指标

序号

控制方法

RF最大偏差

1

PI

0.248

2

AEFPI

0.151

火电机组过程控制主要是看直观的性能指标，RF最大偏差就是一种直观的性能指标。用RF期间的最大偏差衡量AEFPI、PI的外扰抑制性能，相对PI，AEFPI提高了64.2%，说明AEFPI的外扰抑制性能明显高于PI。

根据给出的数学计算比较及仿真结果，得出基本结论3：采用AEFTF构造的AEFPI在提高反馈控制性能上有实质性进步。

6  在难控工程的应用效果验证

首先需要指出AEFPI参数整定的问题，之前的PI、AEFPI参数整定采用了数学最优法。在实际工程中，数学最优法难以采用。现实中，PID参数多用凑试法。

在AEFPI参数整定上，文献[25]提出基于ZN[30]模型（Ziegler-Nichols Model，ZNM）的工程法，简称ZNM参数整定法。ZNM表达为：

（15）

其中，fZNM（s）为ZNM的传递函数，KZN为增益，TZN为时间常数，τZN为滞后常数。

ZNM代表一种过程的工程建模，即建立过程的ZNM。

将ZNM法用于AEFPI参数整定：

（16）

将AEFPI运用于某330 MW供热火电机组的供热蒸汽温度控制的商业技改项目，该系统设计额定参数如下：：

蒸汽压力  3.95 MPa

蒸汽温度  415 ℃

蒸汽流量  195 t/h

实际蒸汽流量长期在50 t/h以下，蒸汽流量变化范围在15～50 t/h。系统设计为PI控制，长期无法投入汽温自动控制。通过现场试验，得到该系统的近似ZNM为：

（17）

其中，fZNM：15（s）为蒸汽流量在15 t/h时的过程模型，fZNM：45（s）为蒸汽流量在45 t/h时的过程模型。简单地认为，蒸汽流量越低，过程纯滞后也越大。

由式（17）可知，在低蒸汽流量工况下，过程模型的时变性较大，特别是纯滞后的比例较大，属于典型的难控过程。

将AEFPI运用于所述供热蒸汽温度控制，如图17所示。图中修正函数[31]用于在不同的供热蒸汽流量下修正AEFPI的参数，目的是对过程的时变问题有较好的跟踪特性。实际系统还包括一些前馈控制[24]。简单说，根据在现场的试验结果，将在高、中、低蒸汽流量下得到的过程特性拟合出一个TAEFI和KAEFPI的修正函数，然后根据实际蒸汽流量，对AEFPI的TAEFI和KAEFPI参数进行修正。其中，在蒸汽流量45 t/h的AEFPI参数，KAEFPI=0.73、TAEFI=266 s。

图17  供热蒸汽温度控制示意图

在蒸汽流量38 t/h，将供热蒸汽温度给定值提高10 ℃，得到的过程控制特性如图18所示，可以看出，采用AEFPI，对所述供热蒸汽温度具有较好的控制特性。

图18  供热蒸汽温度控制特性示意图

长期投用AEFPI的结果表明，AEFPI能够有效抑制扰动，并且减温水调节阀指令输出平稳。因采用AEFPI优化之前已经指出系统设计为PI控制，长期无法投入汽温自动控制，因此没有与PI控制进行对比。

7  结论及展望

针对加速型工程最速比例-积分控制器如何提高反馈控制性能且有实质性进步的本质机理进行了探索，得出如下结论：

a. 揭示出了構造加速型工程最速比例-积分控制器的背后实际上是一种窗函数滤波中从未出现过的直角三角窗函数滤波；

b. 给出了加速型工程最速跟踪滤波器性能优于一阶惯性滤波器、加速型工程最速比例-积分控制器性能优于最优比例-积分控制器的理论依据；

c. 验证了相比于PI控制，基于最速滤波机制构造的最速控制器，在难控过程的适用性、有效性和先进性。

控制科学是试验科学，技术先于理论。自2018年以来，工程研究人员在火电机组控制工程实践中，经过艰辛的探索和无数次反复试验，先后发明了工程最速滤波器（EFTF）、工程最速控制器（EFC）[25]；加速型工程最速滤波器（AEFTF）、加速型工程最速控制器（AEFPI）[26]，并非通过理论研究或者数学推导得出的，该技术已在某省火电机组中大规模成功应用[25]。

在工控领域，EFC、AEFPI的出现代表了新的控制机制的诞生，是对瓦特原理、PID指数型控制机制的继承和发展，本文给出的理论依据证实了AEFPI在提高反馈控制性能上的实质性进步，完成了从PID的指数型控制机制到工程最速控制机制的过渡，是对控制科学发展的重大贡献。

最速控制原理的揭示，是丰富控制理论和控制科学发展的必然要求，笔者抛砖引玉，最速控制原理仍需进一步探索，期待更多学者参与研究，挖掘出更多更实用的研究成果，为控制理论和控制科学的发展与应用做出应有的贡献。

谨以此文，献给以李军为代表的EFC、AEFPI发明团队，向为工业过程控制做出重大里程碑成果的工程师致敬。

参  考  文  献

[1] The editor of Journal of the Franklin Institute.To find the power of a steam engine，on Mr.Watt's principle，in horse power[J].Journal of the Franklin Institute，1827，3（5）：335-336.

[2] 吴海容.复形式导数及其在电机工程中的应用[J].电机与控制学报，2000，4（4）：208-211.

[3] 赵建华，沈永良.一种自适应PID控制算法[J].自动化学报，2001，27（3）：417-420.

[4] 李军，万文军，张曦.基于非线性滤波环节的新型鲁棒PID控制策略的研究[J].动力工程学报，2013，33（2）：117-122.

[5] 谢平平，李银红，刘晓娟，等.基于社会学习自适应细菌觅食算法的互联电网AGC最优PI/PID控制器设计[J].中国电机工程学报，2016，36（20）：5440-5448.

[6] 王维洲，吴志伟，柴天佑.电熔镁砂熔炼过程带输出补偿的PID控制[J].自动化学报，2018，44（7）：1282-1292.

[7] 李军，黄卫剑，万文军，等.一种高性能PID控制器的研究与工程应用[J].广东电力，2018，31（7）：42-48.

[7] 曾喆昭，刘文珏.自耦PID控制器[J].自动化学报，2021，47（2）：404-422.

[8] NYQUIST H.Regeneration theory[J].Bell System Technical Journal，1932，11（1）：126-147.

[9] BODE H W.Network analysis and feedback amplifier design[M].New York：Van Nostrand，1945.

[10] EVANS W R.Graphical analysis of control systems[J].AIEE Trans.Part II，1948（67）：547-551.

[11] 罗传翼，程桂芬，付家才.控制工程与信号处理[M].北京：化学工业出版社，2004.

[12] HALKIN H.Liapounov's theorem on the range of a vector measure and Pontryagin's maximum principle[J].Archive for Rational Mechanics and Analysis，1962，10（1）：296-304.

[13] BELLMAN R.Functional equations in the theory of dynamic programming III[J].Rendiconti del Circolo Matematico di Palermo，1956，5（3）：297-319.

[14] KALMAN R E.On the general theory of control systems[J].Ire Transactions on Automatic Control，1959，4（3）：110-124.

[15] 朱宇轩，李少远.双层模型预测控制系统的多包镇定域分析与系统设计[J].自动化学报，2018，44（2）：262-269.

[16] 李世卿，丁宝苍.基于动态矩阵控制的双层结构预测控制的整体解决方案[J].自动化学报，2015，41（11）：1857-1866.

[17] 尹良震，李奇，洪志湖，等.PEMFC发电系统FFRLS在线辨识和实时最优温度广义预测控制方法[J].中国电机工程学报，2017，37（11）：3223-3235.

[18] 刘勇，胡奇英.离散事件动态系统的状态反馈控制理论进展[J].自动化学报，2000，26（4）：499-508.

[19] AZAR AHMAD TAHER，SERRANO FERNANDO E，KAMAL NASHWA AHMAD.Robust H∞ Loop Shaping Controller Synthesis for SISO Systems by Complex Modular Functions[J].Mathematical and Computational Applications，2021，26（1）：21-66.

[20] 刘向杰，孔小兵.电力工业复杂系统模型预测控制——现状与发展[J].中国电机工程学报，2013，33（5）：79-85.

[21] 黄德先，江永亨，金以慧.炼油工业过程控制的研究现状、问题与展望[J].自动化学报，2017，43（6）：902-916.

[22] 许锋，魏小丽，任丽红，等.基于多变量广义预测控制的不稳定系统控制结构选择方法[J].自动化学报，2013，39（9）：1547-1551.

[23] 司文杰，董训德，王聪.输入饱和的一类切换系统神经网络跟踪控制[J].自动化学报，2017，43（8）：1383-1392.

[24] 高志强.自抗扰控制思想探究[J].控制理论与应用，2013，30（12）：1498-1510.

[25] 李军，黄卫剑，陈锦攀，等.一种适应新型电力系统深度调峰快速调频的工程最速控制器[J].广东电力，2021，34（8）：110-119.

[26] 李军，黄卫剑，陈锦攀，等.一种适应新型电力系统的加速型工程最速比例积分控制器[J].广东电力，2022，35（7）：170-178.

[27] 李军.一种线性最速跟踪滤波器的控制方法、系统及装置：CN113341720B[P].2022-06-10.

[28] 李军，陈锦攀.一种直角三角窗函数的构造方法、装置及滤波器：CN115981599A[P].2023-02-06.

[29] 李军，陈锦攀.一种加速型工程最速微分器的生成方法及装置：CN115016254A[P].2022-07-05.

[30] ZIEGLER J G，NICHOLS N B.Optimum setting for automatic controllers[J].Trans ASME，1942，64：759-768.

[31] 李軍，陈世和，万文军，等.一种内反馈控制器IFC的研究与应用.自动化学报，2018，44（9）：1706-1716.

（收稿日期：2023-06-07，修回日期：2023-10-19）