一种基于小波聚类的NOMA 系统SIC 盲检测算法*

刘 佳，张 浩，王 波

（1.桂林电子科技大学 信息与通信学院，广西 桂林 541004；2.北京三星通信技术研究有限公司，北京 100028）

0 引言

为大规模无线设备和数据传输提供有效支持，是当前5G 及下一代蜂窝网无线通信6G 的主要目标[1]。非正交多址接入(Non-Orthogonal Multiple Access，NOMA)系统在发送端进行了叠加编码技术,且在接收端采用串行干扰消除（Successive Interference Cancellation,SIC）接收机来消减干扰，因此，相比正交多址接入（Orthogonal Multiple Access,OMA）系统，NOMA 系统SIC 具有更高的频谱效率[2]。由于NOMA 系统接收机的正常工作离不开接收端用户设备的网络层参数，比如预编码矩阵指示(Pre-coded Matrix Index,PMI)、调制阶数（Modulation Order）和秩指示（Rank Index,RI）等。然而，这些网络层参数都是由无线资源控制（Radio Resource Control,RRC）信令携带[3]，这些网络层参数在NOMA 系统中传输相对于OMA 系统而言会增加信令的消耗[4]。为了降低信令的开销，需要对多用户的这些动态信令进行全部或者部分盲检测。

目前常用的盲检测算法分为两类，第一类是基于最大似然值的算法，使用最大似然框架用于盲检测算法，其实质是一种融合了多种复合参数假设的检验问题，这类算法最典型的是基于对数最大似然估计（MLLE）算法[3,5-6]；第二类是基于特征的算法，需要利用接收数据的特征来进行决策，比较常见的特征有计算小波变换得到的幅度去掉信号峰值后的方差[7-8]、信号相位、频率或者幅度的方差[9]、统计矩[10]、信号自身数据分布矩、累积量和相关的循环累积量[11-12]等。虽然基于特征的算法并不总是能取得最优解，不过它的实现具有较低的复杂度，可以提供接近性能最优的解决方案。而传统MLLE算法中，虽然利用了数据源的统计特性，但没有考虑到数据内部的相互关系，如几何特征，因而其性能通常会有所损失。在这些研究的启示下，本文利用NOMA 场景的接收星座具有较为清晰的几何特征，采用聚类来实现低复杂度的几何特征提取，提出了基于小波聚类的动态参数联合盲检测算法，解决了盲检测正确率较高时计算时间复杂度 (Computational Time Complexity,CTC) 更高的问题。

1 系统模型

考虑基站与n个用户设备组成的下行传输场景，发送端将所有需要发送给多个用户的信息在频率域进行叠加，这个叠加信号将发送给这个单小区内的所有需要通信的用户，而对于接收端，每个用户都将接收到相同的叠加信号，不同用户间仅因为与基站距离不同而接收信号幅度不同，由此每个用户都需要不同层次的串行干扰删除，以便能在解调当前用户前把其他用户的干扰删除掉。

如图1 所示，对于这n个用户设备的第i个用户，它的二进制信息序列bi进行信道编码、速率匹配和加扰等一系列操作，得到ci序列，ci序列会被映射成正交幅度调制(Quadrature Amplitude Modulation,QAM)符号序列xi，xi为发送给第i个用户的符号序列，xi=，其中xi,k表示基站发送给第i个用户符号序列中第k个符号，LC是候选的调制阶数的个数，是QAM 星座图集合。n个用户采用功率占比组合序列=[α1,α2,…,αi,…,αn]，满足=1。此时，从基站发送的给每个用户的通用的叠加的传输符号序列为：

图1 NOMA 通信系统模型

在传输前，传输符号t通过预编码处理消除部分信道之间干扰，那么在接收端，第i个用户的接收符号的接收表达式为：

其中，Mi表示第i个用户的预编码矩阵，Hi表示第i用户与BS 之间的信道矩阵。gi代表加性高斯白噪声 (Additive White Gaussian Noise,AWGN)，gi服从均值为0 且方差为δ2的正态分布,是独立同分布 (independent identically distributed,i.i.d)，并满足：

式中，E[·]表示数学期望运算，且|·|表示复数的绝对值即取模运算。在接收到叠加信号后，用户并不能简单地直接使用串行干扰删除接收机进行用户分离。如图1 中的虚线框所示，在解调和串行干扰删除前，需要进行多用户的参数盲检测，这个参数盲检测是降低带有 SIC的 NOMA 系统信令开销的重要工作。

2 算法描述

鉴于小波聚类具有比较优秀的计算时间复杂度，提出基于指定输入门限的小波变换参数盲检测算法 (The Wavelet Cluster Algorithm with Assigning Input Threshold,AIT-WC)。AIT-WC 盲检测算法如下：

算法包含执行小波聚类、获取每个聚类的点个数、找到分位点、取平均值、计算过滤器的门限和做判决等步骤。接下来将对这些步骤进行详细解释。

（1）执行小波聚类

在传统的小波聚类中，输入数据的各个维度没有限制数值范围[13-14]。为了排除一些误差点，对接收端接收符号星座图进行小波聚类时，可以设置一个数值范围限制。其原因在于接收符号星座的点在大多情况下是有限的，因为接收符号相对于生成其的标准星座点是正态分布，数据值分布都是围绕着各自的标准星座点的，每个接收符号的值都应该在自己所属标准星座点所在的象限，即接收符号不要相对于生成它的点改变了象限。因此，要在小波聚类之前移除一些可以视为噪点的数值点，将这个每一维度的移除的门限定为T，T的值就是标准星座图的每一个象限的理论区域，可以由式（4）表示:

式中，d是两个相邻星座点的间距，M表示调制阶数，表示的是平行于任一条坐标轴的一条直线所能经过的最多的星座点的数目，(·)max表示取括号内表达式的最大值。那么接收符号的任意一个维度的值v在大于门限T时就需要丢弃这个接收符号，也即满足如下公式时需要剔除:

（2）获取每个聚类的点个数

如果进行聚类之后没有得到类簇，本步骤将被跳过。否则的话，需要获取到每个类簇所包含的接收符号点个数。所有簇所包含的点的个数构成一个序列npc，任一个簇所包含的点的个数就是npc中的某个元素。

（3）找到分位点

并不是所有记录了点个数的簇都是符合最终处理需要的，它们是由于选取的聚类参数而产生的噪点，需要过滤一次。在此阶段，将npc的内部元素按点个数从小到大排列。将排列的npc的前p%的簇当成噪声去除，即排名在前p%的数量较少的簇将被丢弃。此时，去除噪声簇后得到的有效簇序列为sidx。

（4）取平均值

对有效簇序列中的元素所代表的簇取几何平均值，这个几何平均值可以作为对应簇的中心pc值。那么得到的簇中心值与候选的标准星座点cp位置值之间取欧式距离，并对所有有效簇的这个欧式距离求和，就获得了与星座图形状相关的特征值。

（5）计算过滤器的门限

为了确定接收符号在星座图中的分布，可以讨论接收符号在两个标准星座点区域内的近似分布。在这里，可以通过检查每个维度上两个均值和方差已知的正态分布的概率密度曲线的叠加来简化这个问题。下面是两个概率密度函数，其中x为接收到的符号，δ2为噪声对接收机的方差，t为两个相邻的聚类中心之间的距离，因为两个正态分布密度曲线叠加后的曲线的聚类中心一定位于t所在的线段上，也就是说提取出来的表征形状特征的距离一定需要小于这个t值才能表明当前的盲检测参数出于正确区域。

式（6）和式（7）叠加的概率密度函数为如下公式：

对式（8）取关于变量x的导数，并使得这个导数置零如下式：

根据式(9),可以得到函数f3的导数的3 个零点x1=,x2≈0,x3≈t。这3 个零点都是极值点。为了简化讨论，将估计值取成确定值，即设定x2=0,x3=t，并且让3个极值点对应的极值f3(x1)、f1(x2) 和f2(x3)进行比较,以获得一个门限，不符合这个门限则舍弃这个形状特征。f3(x1)在极值点x1=的极值是:

f1(x)的极值是f1(0)，此时：

通过式（12）可以找到t和δ的关系：

t和δ2之间的关系是：

此时，获得了形状特征值的最小门限距离t。式（13）的含义是聚类中心的间距随着噪声功率δ2而变化，如果形状特征值大于这个最小距离门限t时，也即f3(x)＞f1(x)且f3(x)＞f2(x)，那么此时的形状特征值就需要过滤掉。

（6）做判决

判决方法就是取特征向量中元素的最小值索引所对应的盲检测参数。

3 复杂度分析

MLLE 算法的计算时间复杂度为O(N+1)[6]，N表示接收符号个数。相比于传统的小波聚类算法，AITWC 算法无需寻找数据的最大值和最小值，因为事先使用O(N)的比较器将所有数据中超出合理范围的点去除掉了。因此，只需为每个数据点找到所在的网格，计算时间复杂度为O(N)。在进行小波聚类后的步骤中，prctile 和min 函数的计算时间复杂度分别为O(nc) 和O(LclogLc)，其中nc和Lc分别是类的数量和待检测个数，而其他的步骤都是对数据或者候选参数进行线性的操作，其余线性步骤的计算时间复杂度总和为O(4N)，所以小波聚类执行后在 AIT-WC 中剩余的步骤的计算时间复杂度总和为O(4N+nc+Lclog(Lc))。同时，由于N≥nc＞＞Lc，因此 AIT-WC 算法的复杂度总和可以简化为O(N+4N+nc+Lclog(Lc))≈O(6N)。根据上面分析，AIT-WC 算法的计算复杂度与 MLLE 算法的计算复杂度相当。

4 系统性能仿真分析

在本节中，基于前文的分析给出仿真数值性能结果。表1 给出了场景的仿真参数[15]。在仿真中，设置了带宽和载波频率分别为 20 MHz 和 2 GHz，设置用户移动速度为 10 km/h，此时的用户信道环境是用于模拟行人用户设备移动速度的多径衰落的 (Extended Pedestrian A model,EPA) 信道。信道模式设置为多径RAYS模型，上报模式选择的是 PUSCH1-2 模式，传输模式选择的是 TM4 模式，前缀码长度的模式选择的是 Normal形式，发送天线和接收天线数分别设置为 4 和 2，下行信道估计 (Cell Reference Signal,CRS) 选择了DFT(Discrete Fourier Transform)方法。仿真所涉及的两个盲检测参数为 PMI 和调制阶数，为了简化每次仿真两者的排列组合，两者的范围分别设置为[1,2,3,4] 和[2,4,6,8]。除此之外，为了表现盲检测正确率与SNR（Signal-to-Noise Ratio）值的关系，本次仿真设置了 SNR 范围为SNR={snr|snr=0,1,…,36}。通过根据表格2 设置的仿真参数进行盲检测仿真实验，获得了如图2～图5 所示的仿真结果。

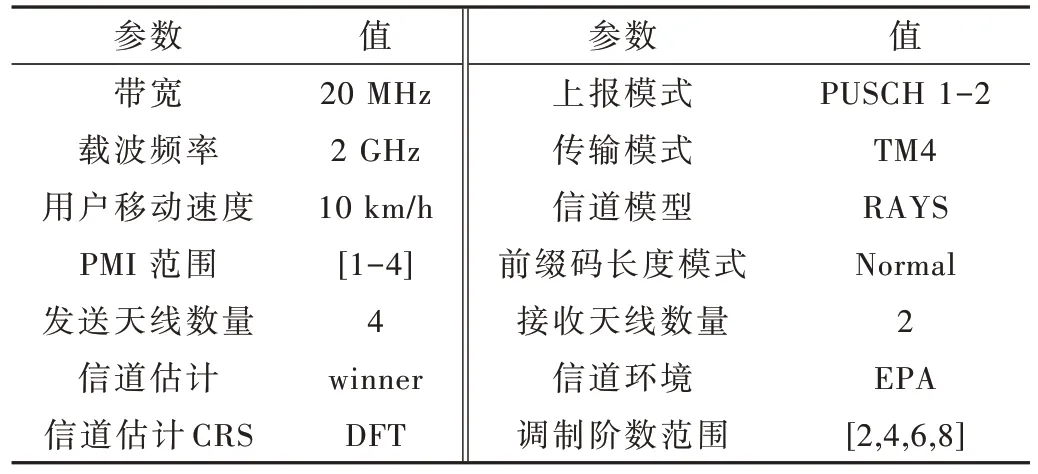
表1 仿真参数

图2 用户数为3 的盲检测正确率曲线比较

图2 是在 PMI 固定为 1 时的关于盲检测正确率曲线的比较。图中显示，提出的AIT-WC 算法的盲检测性能要优于 MLLE 算法。同时，从图2 还可以看出，当联合调制阶数达到 12 时，AIT-WC 算法能在 SNR 为 36 dB 左右达到盲检测正确率为 100%，而MLLE 算法无法达到，说明对于高阶联合调制而言，AIT-WC 算法的检测性能更具优势。图3 是在PMI 固定为1 时的链路级吞吐量比较,从图中可看出，当调制阶数以及SNR 相同时，AIT-WC 算法的吞吐量优于MLLE 算法的吞吐量。同时，当联合调制阶数达到12 时，AIT-WC 算法在 SNR为 36 dB 左右达到吞吐量峰值，而MLLE 算法无法达到，说明对于高阶联合调制而言，AIT-WC 算法的吞吐量性能也更具优势。

图3 用户数为 3、4 和 5 的吞吐量比较

图4 与图5 都是用户数为 4 时，PMI 在 1 和 3 变动时的盲检测正确率曲线，可以看出，在PMI 变动时，AITWC 算法与MLLE 算法在SINR 相对较低时呈现的性能差异不大；而当SINR 增加，盲检测性能差距拉大，尤其对于MLLE 算法更明显。例如，图5 中当SNR 为34 dB时，对于PMI 从1 变动到3，MLLE 算法的检测正确率从35%变化到20%，而AIT-WC 算法的检测正确率从98%变化到97%。此结果进一步印证了AIT-WC 算法由于过滤噪声处理而具有的更优稳健性。

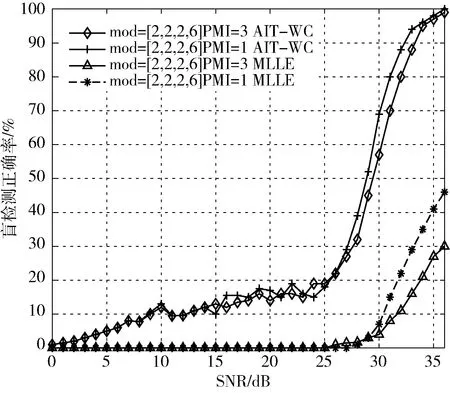
图5 联合调制阶数为12 的 PMI 影响下的盲检测正确率曲线

5 结论

通过对星座图的形状特征的利用，本文提出了一个基于小波聚类的多参数盲检测算法，新提出的算法利用到了聚类中的网格法，同时也区别于传统网格法的使用，根据研究的场景进行了合理的设计。仿真结果表明，新提的 AIT-WC 盲检测算法在仿真结果中的性能要优于经典的 MLLE 算法，且计算时间复杂度与 MLLE算法相当。但随着联合调制阶数增大，AIT-WC 与MLLE 算法的盲检性能均有较明显下降。下一步可继续研究在联合高阶调制方式下更高检测性能的盲检测算法。