基于GPU 的稀疏深度神经网络性能优化*

石于诚，黄建强，边浩东，吴 利，贾金芳，王晓英

（青海大学 计算机技术与应用系，青海 西宁 810016）

0 引言

随着神经网络原理性研究的不断深入以及算力逐步增强，越来越多的深度神经网络涌现。例如在自然语言处理[1]领域，谷歌提出Transformer[2]模型，其本身对于梯度消失这一难题的解决以及可以进行并行训练等一系列的优势，使得大模型愈发火热，ChatGPT[3]也是在此基础上训练得到的。但规模庞大的深度神经网络对于模型应用的时效性提出了更大的挑战，由于“存储墙”[4]和“功耗墙”[5]的存在，稀疏深度神经网络[6-7]进入研究视野，GPU 设备和稀疏深度神经网络的结合使得训练速度再迈上一个崭新的台阶。

但目前稀疏深度神经网络于GPU 的运行性能仍然存在提升空间，异构计算平台的运算能力还没有能够得到充分发挥。虽然稀疏深度神经网络在存储和计算上存在优势，但同时也会带来负载不均衡和空间局部性差的缺点。图计算领域最有影响力的高级比赛之一：GraphChallenge[8]，新开设了与稀疏深度神经网络有关的赛道，2019 年的优胜者之一，Bisson[9]等研究者将计算任务分配给GPU 不同的线程，并采用填充等方法尽量消除不同线程之间计算量的差距，并且利用NVLink 和NVSwitch 构建出SMP 结构的集群体系，实现数据的快速获取。之后的Lin[10]等研究者进一步使用了任务图优化技术，将任务图重新构造为有向无环图，消除重复的节点的计算，使得同一节点的计算结果可以被相关节点所共享。

现有研究者大多针对于稀疏深度神经网络并行计算时负载不均衡的问题进行解决，而在空间局部性方面仍然有待进一步研究。为此本文针对稀疏深度神经网络的计算顺序进行调整，增强空间局部性，并结合GPU的独特结构以及CUDA 编程的优化方法，最后相较于cuSPARSE 相关库函数在网络层数为480 层时获得1.67倍的性能提升，在网络层数为1 920 层时获得2.5 倍的性能提升。

1 相关工作

1.1 神经网络稀疏化

深度神经网络存在训练时间长、速度缓慢等缺点，对于硬件设备的要求也越来越高。为降低计算与存储成本，神经网络稀疏化成为研究热点。

在大规模计算过程中，存在许多冗余的参数与计算，而对于冗余内容进行剪枝并不会过于影响模型最终训练精度。Arora[11]等指出，数据集在概率统计上的分布可以用稀疏的网络结构表示，在对于最终激活的神经元与具备高度输出的聚类神经元进行统计与分析之后，可以构建出较优的稀疏网络拓扑从而获得更快的训练速度。

Cun[12]等提出了经典的Optimal Brand Damage 算法，通过在删除参数之后对于目标函数的变化进行观测来确定每个参数实际的贡献度，而参数具体对于目标函数的影响如式(1)所示：

该式计算较为繁琐，通过对角逼近理论可以将公式进行简化，如式(2)所示：

每个参数的贡献度则通过式(3)可以计算得到，最后将计算数值较低的参数删去，则在保证模型训练精度的前提下对于模型训练速度进行了提升。

神经网络稀疏化的意义不仅在于提升模型训练速度，对于模型的泛化能力同样也进行了提升。神经网络的稀疏化也不只存在于网络结构的设计层面，针对于采样噪声研究者们提出了正规化和一些权重惩罚[13]举措；为了避免模型过拟合，研究者们提出了dropout[14]方法对于全连接层进行剪枝。这些方法共同造就了深度神经网络的稀疏性，即在精度、训练速度与泛化能力三个方面获取平衡。

1.2 稀疏矩阵存储格式

为了节省存储空间并提升计算效率，稀疏矩阵通常被压缩存储，即只保留有效的非零元素进行计算。

朴素的稀疏矩阵压缩存储格式是通过三个数组分别对于非零元素的行偏移、列偏移具体数值进行存储。但这样的存储方式显然是冗余的，对此CSR（Compressed Sparse Row）[15]存储格式进行了优化，虽然CSR存储格式仍然使用三个数组进行存储，但没有存储每个非零元素的行偏移，只标识了稀疏矩阵中每行第一个非零元素地址和第一行的首地址之间的偏移，在数值上即表示为从第一行开始到索引所对应的行当中非零元素的个数。

在此种压缩方式下，稀疏矩阵中的非零元素的行偏移只需要根据每行的非零元素个数进行确认即可，列偏移和数值的存储数组长度仍然和稀疏矩阵中非零元素数目保持一致。CSR 存储格式通过这样的方式进一步对于存储空间进行了压缩，也进一步减少从数组中读取元素信息时所存在的数据依赖，提升可并行性，具体如图1 所示。

图1 CSR 压缩存储格式

2 优化方法与实现

GraphChallenge 给出的数据集稀疏度为0.03，分布并无明显规律，本文对于朴素计算方式进行调整，配合相应存储结构获得更好性能提升。

2.1 计算顺序优化

随着深度学习研究的不断深入，普通的GPU 设备已经开始无法满足层数更深、参数规模更大的神经网络的训练，研究者们将目光转向硬件平台结构的进一步优化，例如Google 所提出的TPU，NVIDIA 推出的DGX-2系统平台。而在硬件领域，存在一个经典的优化思想：权重固定(Weight Stationary)，如图2 所示。根据Sze[16]等研究者的研究表明，神经网络在训练时的瓶颈在于内存访问，针对于全连接层而言，运算的基本组成部分是乘法与累加操作，而每一次的乘法与累加都需要多次的存储器读取和一次的存储器写入，而这多次的访存操作，在最坏的情况之下，都需要对于片外存储器进行访问，而访问片外存储器往往会带来更多的延时。于是硬件加速器的设计者们引入层级更多的内存架构进行数据的存储，以便于提升访存速度。并由于神经网络的训练流程相对固定，将哪些数据在哪个时刻预先读入哪个分层存储器结构中成为了运算速度优化的重点。

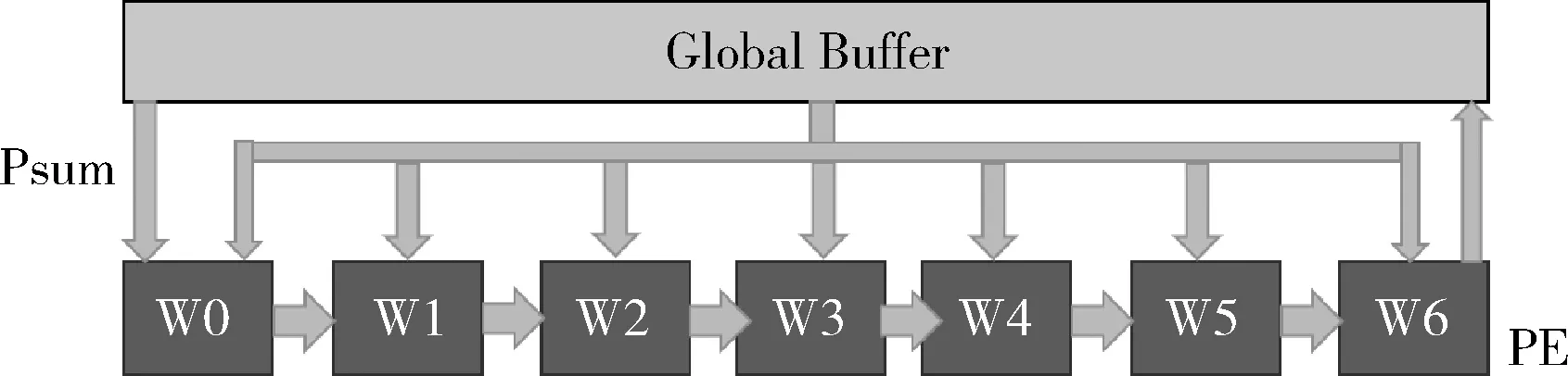
图2 权重固定

上述所提及的优化思路被称为神经网络的数据流问题，而权重固定便是神经网络数据流的种类之一，权重固定的具体思路是将权重读取到存取效率较高、能量消耗更小的寄存器当中，并减少低效的访存操作，针对权重数据尽可能实现更高的数据复用，并且计算所得出的部分和可以通过处理引擎阵列进行广播，从而进行部分和的累加操作。

这样的硬件设计优化思路运用到软件的设计方面，即为数据重用性的增强。具体方法为将数据预取到访存延迟较低的存储结构内，并最大化预取数据的使用，避免频繁的数据读写替换，加速整体计算。

2.1.1 优化实现

通过观察稀疏深度神经网络的具体运算过程，核心部分为输入矩阵和权重矩阵的相乘。朴素算法为多次矩阵向量乘的叠加，如图3 所示。

图3 朴素稀疏矩阵乘法

朴素的稀疏矩阵乘法不外乎通过压缩矩阵存储，提升计算效率，但核心计算顺序与稠密矩阵计算一致。

这样的计算顺序是缓存不友好的，并且不具备良好的空间局部性，每次对于新的行元素的访问都会造成缓存不命中，并且可能造成缓存抖动的发生。即使通过矩阵转置变换为行元素与行元素之间的相乘，计算结果的转置也会带来额外的开销，而在大规模的矩阵乘法中，为了节省存储空间，往往使用已经开辟的矩阵空间进行存储，在此情况下，行元素将被不同行的计算所使用，无法直接将计算结果存储于原位置，并且对于各个线程计算任务的划分也会造成阻碍。

为此本文针对其计算顺序进行调整，每一次计算将输入矩阵的一个元素分别与权重矩阵的行元素相乘，该两两元素相乘的结果直接保存于权重矩阵每行元素的对应位置，接着将输入矩阵后一元素与权重矩阵的下一行元素分别相乘，元素相乘结果分别累加于上一次计算的结果，并存储于相同位置，而由于计算结果的覆盖存储，每个计算任务中保留权重矩阵行元素的副本以获得正确结果。每次遍历输入矩阵的一行并完成相应计算后即可获得矩阵相乘结果的一行数据，如图4 所示。

图4 计算顺序调整

在计算任务划分时，假如仍然按照行元素进行划分，在上述的计算顺序调整后，每次计算仍然需要权重矩阵不同行的数据，程序空间局部性差。为此选择按列划分计算任务，并且结合分块技术，每个计算任务内使用部分列元素计算，该部分列元素仍然预取至线程私有寄存器内。

基于上述的计算顺序与任务划分的调整，每个计算任务内所使用数据皆被预取至寄存器内，无需额外冗余访存，增强程序局部性，提升计算性能。为了性能的进一步提升，可为一个计算任务分配一个线程束(Warp)，对于元素的遍历相乘采用循环展开的方式进行计算，细化任务粒度，并且由于不同计算任务之间不存在数据依赖，无需同步等待，并行计算不会退化为串行。虽然输入矩阵与权重矩阵都是稀疏矩阵，导致不同计算任务的负载不均衡，但本文对于计算任务的划分是循环进行，同一线程束计算不同的部分列元素，并且数据集中的非零元素并不存在上三角或是下三角等特殊分布，因此每个线程束的计算任务方差较小，缓解负载不均衡。

2.1.2 优化结果分析

缓存命中率可以作为反映程序空间局部性的指标，在传统计算方式中，由于每次需要将矩阵的行元素分别与另一矩阵的列元素相乘累加得到结果，即需要读取两个矩阵的一行元素与一列元素。以矩阵大小为1 024×1 024，每行平均非零元素占比为25%，缓存行(cache line)大小为64 B 为例，由于double 类型占8 B，一个缓存行可以存储8 个元素，而访问矩阵一行元素则会出现32 次缓存未命中，访问矩阵一列元素会出现256 次缓存未命中，缓存命中率只有43.75%，但经过计算顺序的调整后，每次的计算只需要访问输入矩阵中的一个元素与权重矩阵中一行元素，总共出现33 次缓存未命中，缓存命中率为87.16%，程序具备良好空间局部性。

2.2 存储方式优化

通过调整计算顺序以提高空间局部性，数据访问更加集中，将其预读至读写延迟更低的存储结构中，能够进一步提升性能。CUDA 内存模型[17]提供了分层存储结构，包括寄存器、共享内存、L1 缓存、L2 缓存和全局内存。其中，寄存器是每个线程私有的存储空间，访问速度最快，但容量有限；共享内存是每个块私有的存储空间，访问速度比全局内存快，容量介于寄存器与全局内存之间；L1 缓存和L2 缓存是全局内存的缓存，访问速度比全局内存快，但容量有限；全局内存是所有线程共享的存储空间，访问速度最慢，但容量最大。

2.2.1 数据存储优化

出于存储容量和读写延迟等因素的综合考虑，本文将数据预取至共享内存中。不读取至寄存器主要有以下两个原因：(1)寄存器存储容量有限；(2)寄存器是每个线程所私有的，于是每个线程都需要保存一份整行数据的副本，整体容量将会超出限制。

但共享内存存在存储体冲突的可能性，为了提升内存带宽，共享内存被划分为32 个存储体，不同的存储体可以被同时访问，从而实现流水线式的数据读取，隐藏数据读取延时。但同时也带来了新的问题，假如同时有多个线程对于同一个存储体进行访问，此时这些线程只能排队对于存储体进行访问，从并行读取退化为串行读取，此时的访存时间将变为并行访存时间的线程访问数量的倍数，从而对于程序性能造成负面影响，如图5所示。

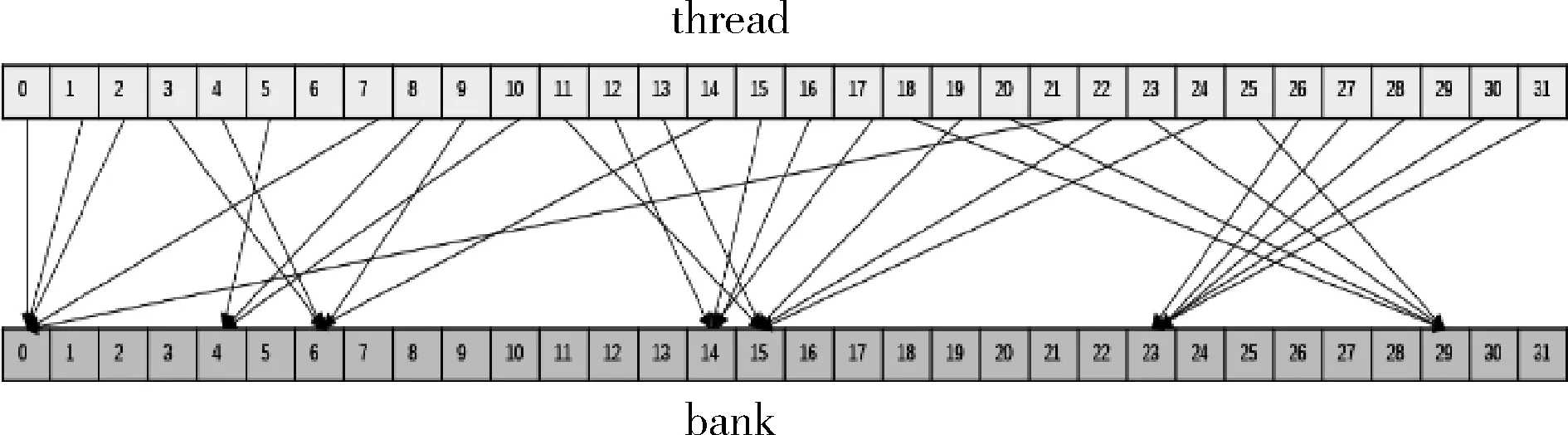
图5 存储体冲突

虽然CUDA 对于共享内存的访问还支持广播的方式，即线程束内的所有线程都只访问同一个存储体，被访问的内容便将广播到所有进行访存请求的线程当中，此时虽然只需要进行一次广播，但由于只有一个存储体被访问，带宽利用率较低，无法充分发挥硬件能力。所以在设计线程的具体执行流程的时候，需要尽量保证一个存储体在同一时刻只有一个线程进行访问。

而由于设计者已经将共享内存包含的存储体数量与线程束所包含的线程数目进行了对应，本文的程序设计也相应更加方便。在使用线程束对于共享内存进行访问之时，只需要尽量使得每个线程的任务映射到各不相同的存储体内即可，尽可能降低存储体冲突发生的可能性，从而获得较高的访存效率和较好的程序执行性能。经过上文计算顺序的调整，输入矩阵内的同一列元素将同时被多个线程访问，而不同行的同一列元素可能存储于同一个存储体内，使用内存填充可以使得本位于同一存储体内的元素分布在不同存储体内，如图6所示。

图6 内存填充

2.2.2 数据依赖消除

本文选择了CSR 格式作为稀疏矩阵的压缩和存储格式，因非零元素分布不规律且散乱，无特定的规律。同时，CSR 格式也最适合上文所提出的计算顺序。

CSR 格式的数据依赖为每行的非零元素数量的计算，需要根据前一行的非零元素数量计算。而本文对CSR 格式进行了修改，因每行非零元元素个数较少，压缩后填充为小规模的稠密矩阵，每行元素位置位于特定区间，便于直接标记每行非零元素数量，以此消除数据依赖。

在并行计算过程中，线程束在完成一行的计算任务后，只需要统计本次计算所产生的非零元素数量，并直接更新相应位置上的数值，无需进行线程之间的同步，以此消除数据依赖。

3 性能测试与验证

GraphChallenge 官方所提供的性能分析指标，除了运行时间外，还提供了运行速度的计算,具体计算方式为：输入矩阵的行数和连接数目的乘积，最终除以运行时间。通过分析不同方法在不同维度的稀疏深度神经网络中的性能表现，综合分析不同方法的整体计算性能。

3.1 数据集介绍

GraphChallenge 官方提供了稀疏深度神经网络训练的数据集，内容包括输入矩阵、每层的权重矩阵以及最后的训练结果。官方通过使用Radix-Net[18]生成了稀疏DNN，并通过随机重复与排列的方式生成了不同维度的神经网络。本实验所选择的数据集，输入矩阵的大小为60 000×1 024，权重矩阵的大小为1 024×1 024，输出的结果矩阵大小为60 000×1 024，表1 展示了数据集的详细规模。

表1 数据集规模

3.2 实验流程

实验流程即为基于GraphChallenge 所给数据集进行稀疏深度神经网络的训练，具体流程如下：

(1)从数据集文件当中，将输入矩阵和权重矩阵的数据读入内存；

(2)计算出每层的输入矩阵和权重矩阵的乘积，并对于计算结果都加上偏置的数值，接着将计算结果输入激活函数ReLU 当中得到最后的数据；

(3)通过训练的结果矩阵当中的非零元素，计算得到最终的分类结果；

(4)将获得的分类结果和官方所提供的答案进行对比，确认计算结果的正确性；

(5)输出流程(1)～(2)的具体执行时间作为程序的性能结果。

3.3 具体性能对比

实验对比是使用cuSPARSE 库函数版本和本文利用CUDA 所实现优化方法的对比，测试在集群上进行，具体配置为：CPU Intel Xeon Silver 4110，GPU Tesla V100-PCIE-32GB，NVCC 11.2，程序开启了O2 优化，具体的运行结果如表2 所示。

表2 不同版本程序运行时间比较

将运行时间代入官方所提供的运行速度的计算公式中，得到的具体结果如表3 所示，最终对比如图7所示。

表3 不同版本程序运行速度比较

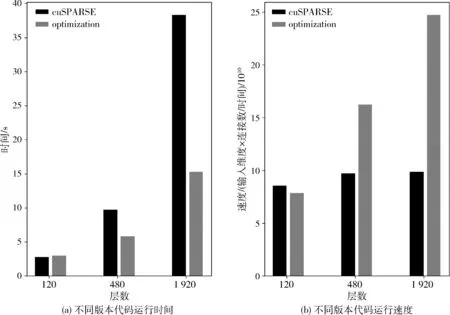
图7 不同版本代码运行结果比较

根据最终结果，可以看出将CUDA 编程的相关优化方法与特定的计算和存储优化相结合所体现出的性能优势。而之所以随着层数的不断扩大，本文所实现的优化方法的性能提升同样增大，主要原因之一在于大量的计算与数据传输的重叠而产生的时间隐藏。同时从对比可以看出GPU 设备在计算密集型任务上相较于CPU所存在的巨大优势，以及将计算顺序的调整、相关存储的优化与CUDA 编程的相关优化内容相结合之后所产生的性能优势，并且随着网络层数的增加，这样的性能优势也变得更加明显，验证了本文所实现的性能优化方法的优越性。

4 结论

大模型是未来发展的趋势之一，但如何有效降低运行与存储成本成为了关键问题，而针对神经网络的稀疏化处理不仅能够降低计算与存储开销，还可以提升模型泛化的能力。但稀疏化同样也带来了负载不均衡和程序空间局部性差的问题，于是如何对于该问题进行解决从而进一步提升计算性能成为研究热点。而本文对稀疏深度神经网络的计算顺序进行了调整，加强数据访问的集中性，并提升程序空间局部性，基于此使用数据预取和CUDA 编程的相应优化手段，进一步获得了性能的提升，实验结果也验证了该方法的优越性。