巧思维切入，妙方法应用——一道三角函数求值问题的探究

■陈 婷

三角函数的求值问题,融合了三角函数的基本概念、基本公式、三角函数的图像与性质等,是三角函数的难点之一,成为高考命题中的一个重要考点。此类问题,知识交汇融合,思维视角多样,方法技巧多变,是全面考查数学“四基”与数学能力、展示知识交汇与体现方法多样性的一个重要场所,倍受大家的关注。

一、问题呈现

二、问题破解

解后反思:根据所给分式进行整式化处理,是解答这类问题比较常见的一种切入方式。解题时,利用三角函数的平方关系进行合理拆分、合并、化简,构建更为简捷的三角关系式,为进一步求值提供条件。

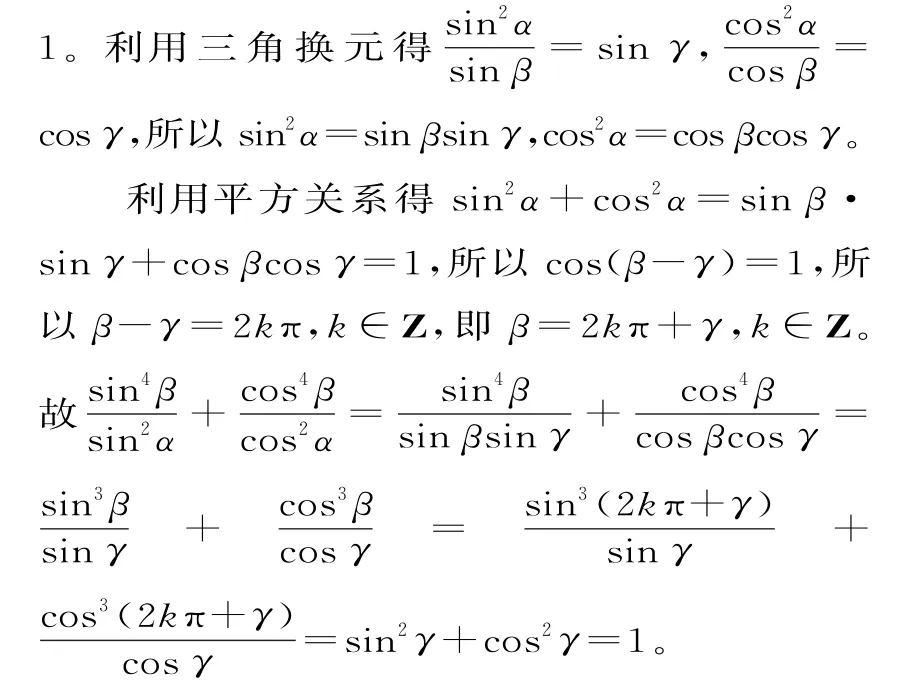
解后反思:根据所给分式的结构特征进行平方转化,为三角换元奠定基础。在三角函数问题中进行三角换元处理,是解决此类问题的一种“巧技妙法”。

解后反思:根据所给的高次幂关系式,通过巧妙代数换元处理,把三角函数问题转化为代数式问题,通过代数式的化简与运算达到巧妙解决三角函数问题的目的。

解后反思:根据所给的三角函数关系式,借助合理的等式配凑与转化,通过基本不等式、柯西不等式加以巧妙放缩与变形,利用等号成立的条件的应用,求得三角函数的值。

解后反思:根据“小题小做”的思维方式,在解答一些选择题或填空题时,可以借助特殊思维,利用特殊值法进行巧妙处理,这里分别从特殊角入手加以分析,从而实现特殊思维应用的目的。利用特殊值法处理问题,有其特殊性,但不具备普遍性。