轮轨异常磨耗下的动车组振动特性研究
2023-12-21何辉永郭冰彬孙效杰王恒亮
何辉永, 郭冰彬, 孙效杰, 王恒亮, 严 建
(1.中车株洲电力机车有限公司 大功率交流传动电力机车系统集成国家重点实验室, 湖南 株洲 412001;2.上海应用技术大学 轨道交通学院, 上海 201418;3.中国铁路上海局集团有限公司科学技术研究所, 上海200333)
由于动车组高速、高密度地服役,其轮轨异常磨耗出现的概率相比普速铁路大幅度上升,这将会影响轮轨间相互作用,引发车辆-轨道系统的异常振动,加剧各层级部件的疲劳损伤,对行车安全性、稳定性和舒适性造成严重威胁[1-4]。因此,亟待对动车组在轮轨异常磨耗下的振动特性进行研究,总结其振动响应规律,为动车组减振设计和运营维护提供理论支撑。
动车组出现的轮轨异常磨耗以踏面凹磨和车轮多边形为主,国内外学者已对此取得一定的研究成果。文献[5-6]试验研究了特定阶数车轮多边形对车轮、轴箱的振动响应影响,证明了车轮多边形是引发轮对、轴箱异常振动的原因;文献[7-8]仿真分析了车轮多边形对动车组各层级时域响应特性的影响;文献[9-10]将实测踏面廓形与车辆-轨道耦合模型相结合,研究踏面凹磨对车辆安全性、平稳性的影响。上述研究较为全面分析了车轮多边形、踏面凹磨对车轮、构架、车体的时域振动影响,也解释了发生某些异常振动的原因。周劲松等[11]通过车体模态分析,建立高维度刚柔耦合模型,研究了车下设备的频域振动响应规律。文献[12]针对地铁异常振动问题,考虑轨道不平顺和踏面凹磨,理论分析了不同频段、不同激扰源对车体部件的影响。文献[13]通过实测构架加速度数据和仿真分析,研究了动车组振动特性及传递规律。
以上研究从时域、频域分析了动车组的振动特性,但大都关注于轮轨异常磨耗对车辆系统某一层级或特定部件的振动响应特性,对车辆系统整体的响应情况关注较少。因此本文在前人研究基础上,分别设计了车轮多边形和踏面凹磨工况,前者考虑车轮多边形波深、阶数,后者考虑凹磨中心位置、磨耗深度、磨耗宽度,分析动车组各层级时域、频域振动响应特性及振动传递规律。
1 轮轨异常磨耗
1.1 车轮踏面凹磨
车轮踏面凹磨指车轮外形大范围低锥度的踏面接触区磨耗,也是动车组车轮磨耗常见的形式之一,严重的踏面凹磨是引发构架横向失稳的主因[14]。参照文献[10]中凹磨磨耗参数的定义方法和踏面廓形数据,忽略了非中心磨耗带的微小磨耗,生成了不同磨耗程度的踏面凹磨文件,其踏面几何外形如图1 所示,凹磨磨耗参数如表1 所示。

表1 凹磨磨耗参数Tab.1 Hollow-worn wheel tread parameters

图1 踏面几何廓形Fig.1 Profile of wheel tread profile
1.2 车轮多边形
车轮多边形指车轮圆周方向上的非均匀磨耗,车轮半径沿车轮圆周呈现周期性变化,多边形以一定的波长延伸至整个圆周表面,相应的波数称为多边形阶数,多边形的峰谷半径差称为波深[15]。车轮多边形为车轮不圆顺的典型形式,其车轮不圆度r的数学表述为
式中:a为多边形波深;μ为谐波次数;φ为相位角。
本文采用simpack 的untrueness 模块,以Harmonic function 方式定义车轮多边形参数,其表达式为
式中:A为多边形波深;n为多边形阶数;β为相位角。
2 车辆-轨道耦合模型
2.1 车辆-轨道耦合模型的建立
为了研究轮轨异常磨耗下的动车组各层级振动特性,参照相关动车组建立了车辆-轨道耦合模型。模型包含了车体、构架、轴箱、轮对、一系悬挂、二系悬挂。其中部分减振器考虑了其非线性特性,其在simpack 界面完成的模型如图2 所示。
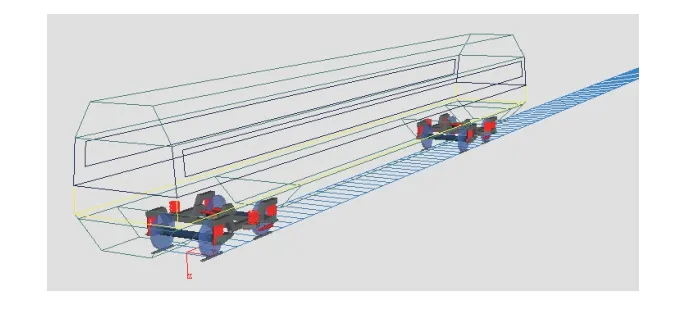
图2 车辆-轨道模型Fig.2 Vehicle-track model
2.2 车辆-轨道耦合模型的验证
为检验模型的可靠性,设置德国低干扰轨道谱,仿真速度为250 km/h。图3 给出了各层级的时域响应,图4 给出了经过FFT 的各层级频域响应。
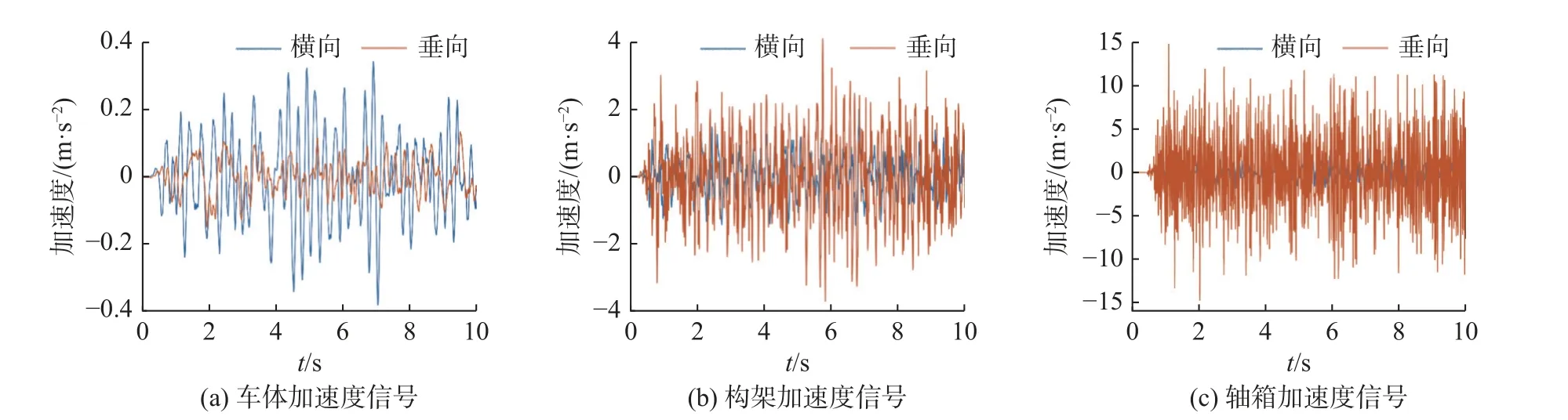
图3 车辆系统各层级时域响应信号Fig.3 Time domain response signals at all levels of the vehicle system

图4 车辆系统各层级频域响应信号Fig.4 Time domain response of rail vehicle system
由图3、图4 可知,车体垂向主频为1.4 Hz,横向主频为2.1 Hz;构架垂向主频为7.2 Hz,构架横向主频为4.1 Hz;轴箱垂向主频为169.8 Hz,轴箱横向主频为3.5 Hz。参照文献[13]中相关数据,经过综合对比,基本验证了模型的可靠性。
3 动车组振动特性分析
3.1 踏面凹磨对动车组振动特性的影响
文献[10]的相关实验数据指出磨耗踏面对应的构架振动加速度明显大于镟修踏面对应的构架振动加速度。通过分析其功率谱密度频谱图,在高磨耗条件下,5.0~12.0 Hz 区段增长最为显著。而构架的自振频率也在5.0~12.0 Hz 区段内,引起构架横向失稳的情况。
参考文献[10]的实验数据和结论,以本文搭建的动车组模型为研究对象,对比分析在5 种不同运行里程下的凹磨踏面对动车组各层级振动响应情况。钢轨廓形文件采用CHN60 钢轨相关参数,轨道激励谱采用德国低干扰谱,仿真时速与文献[10]中的设置相同均为250 km/h。
依次更换根据表1 参数制作的磨耗踏面文件,其各层级的频域响应情况如图5、图6 所示,表2计算了各工况的Sperling 平稳性指标。
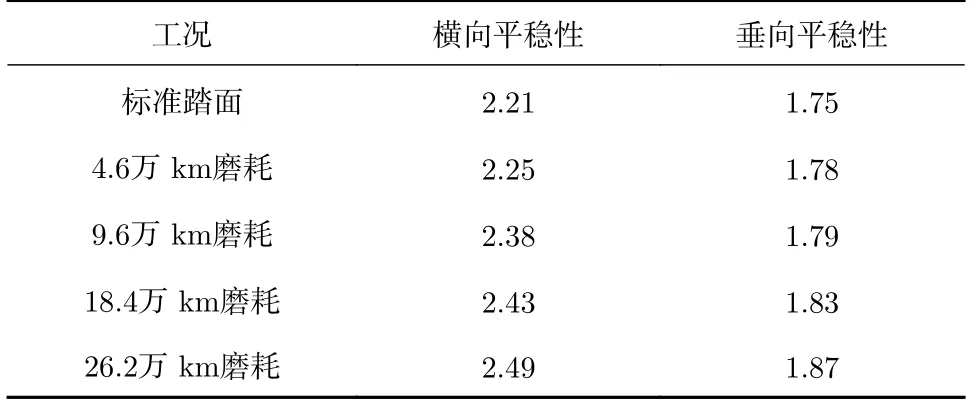
表2 平稳性指标Tab.2 Riding index

图5 不同空心磨耗踏面的轨道车辆系统时域响应信号Fig.5 Time-domain response of rail vehicle system with different hollow-worn tread

图6 不同踏面凹磨下的车辆系统各层级频域响应信号Fig.6 Frequency-domain response of rail vehicle system with different hollow-worn tread
由图5 和表2 分析可知,随着各项凹磨磨耗参数的增加,各层级的时域振动加速度幅值有不同程度的上升,轴箱、构架的加速度振动幅值变化明显,车体的加速度振动幅值由于悬挂系统的存在变化幅度较小。此外,统计数据反映出车体的横向稳定性对于踏面凹磨磨耗程度较为敏感,验证了标准构架横向加速度评价方法的有效性。
由图6 分析可知,踏面凹磨程度对于各层级垂向加速度功率谱分布影响不明显,但对构架、轴箱横向加速度功率谱分布影响显著,特别是构架。随着磨耗程度的加剧,轴箱、构架的频率分布有向右偏移的趋势,高频区域宽度逐渐增加,构架横向高频区从1~8 Hz 扩大为2~28 Hz、6~30 Hz,区域频带响应幅值增加明显,构架发生横向失稳的概率增加。
3.2 车轮多边形对动车组振动特性的影响
图7、8 展示了波深为2 mm 时车轮多边形阶数对动车组振动特性的影响。由图7 可知,随着阶数的增加,各层级的时域振动响应先加剧后减弱,当阶数为7 时,振动响应最大。模型中轮对名义滚动圆半径为0.46 m,仿真时速为250 km/h,计算可知1、3、5、7、9、11 阶车轮多边形分别对应24、72、120、168、216、264 Hz,图8 验证了理论计算的正确性。图9 从时域角度展示了当阶数为1 时,不同波深对各层级振动特性的影响。由图可知,波深的增加使各层级的振动响应有不同程度的加剧,对各层级频谱分布无明显影响,波深仅影响部分频段的幅值。图10 从频域角度展示了不同波深对车体振动特性的影响。由图可知,24 Hz 处的波峰来源于1 阶车轮多边形对应的激励频率,0.99 Hz 为车体的固有频率。随着波深的增加,频谱分布无明显变化,各处幅值有不同程度的增加。其它层级有类似的规律,此处不再赘述。

图7 不同阶数下的车辆系统各层级时域响应信号Fig.7 Time domain response of rail vehicle system with different wheel polygon orders

图8 不同阶数下的车辆系统各层级频域响应信号Fig.8 Frequency domain response of rail vehicle system with different wheel polygon orders

图9 不同波深下的车辆系统各层级时域响应信号Fig.9 Time domain response of rail vehicle system at different wheel polygon amplitude

图10 不同波深下的车辆系统各层级频域响应信号Fig.10 Frequency domain response of carbody with different wheel polygon amplitude
3.3 车轮多边形对动车组振动传递特性的影响
振动传递率是衡量动车组振动特性的一个主要指标,它直观展示了振动能量在悬挂系统中的衰减情况。为进一步研究车轮多边形和踏面凹磨对动车组振动传递特性的影响,图11 和图12 分别展示了车轮多边形的波深和阶数对一系、二系垂向振动传递率的影响。从图11 和图12 可知车轮多边形的波深、阶数变化对车辆一系、二系垂向振动对振动传递率影响幅度较小;构架至车体的垂向振动传递率在高于2 Hz 频带时小于1,说明悬挂在此频带范围内有良好的衰减作用。一般人体对垂向4-8 Hz 的振动频率最敏感,因此车辆悬挂系统满足乘坐平稳性的要求。
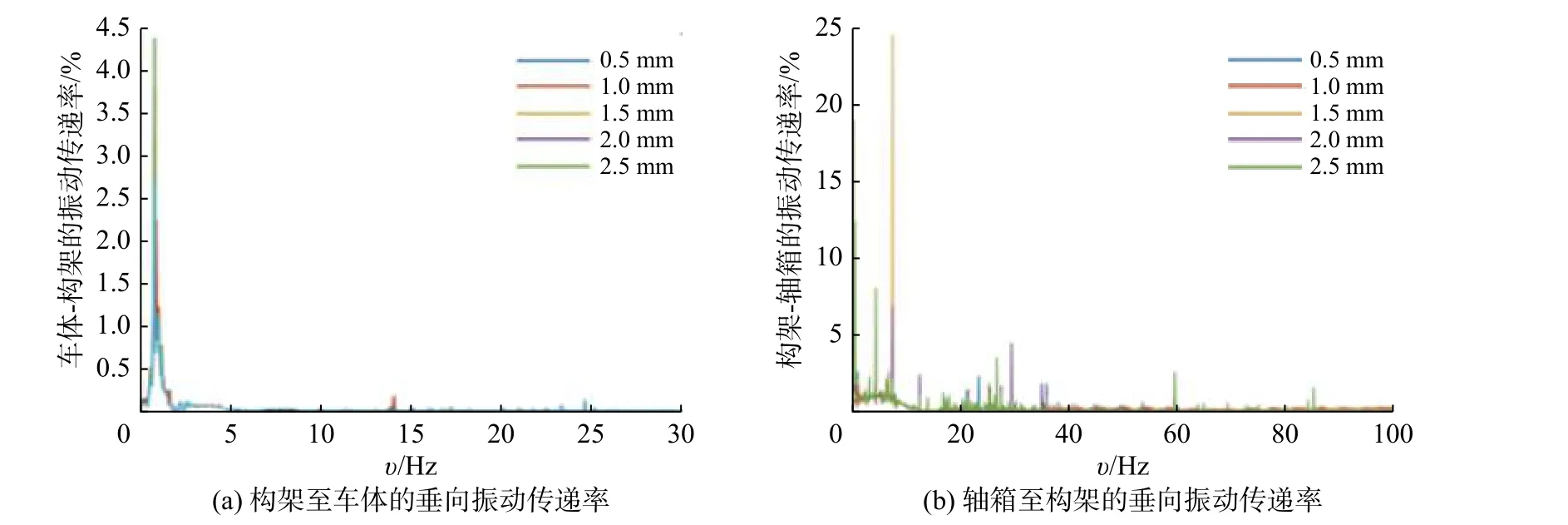
图11 车轮多边形波深对一系、二系振动传递率的影响Fig.11 Influence of wheel polygon amplitude on vibration transmissibility of primary and secondary suspension
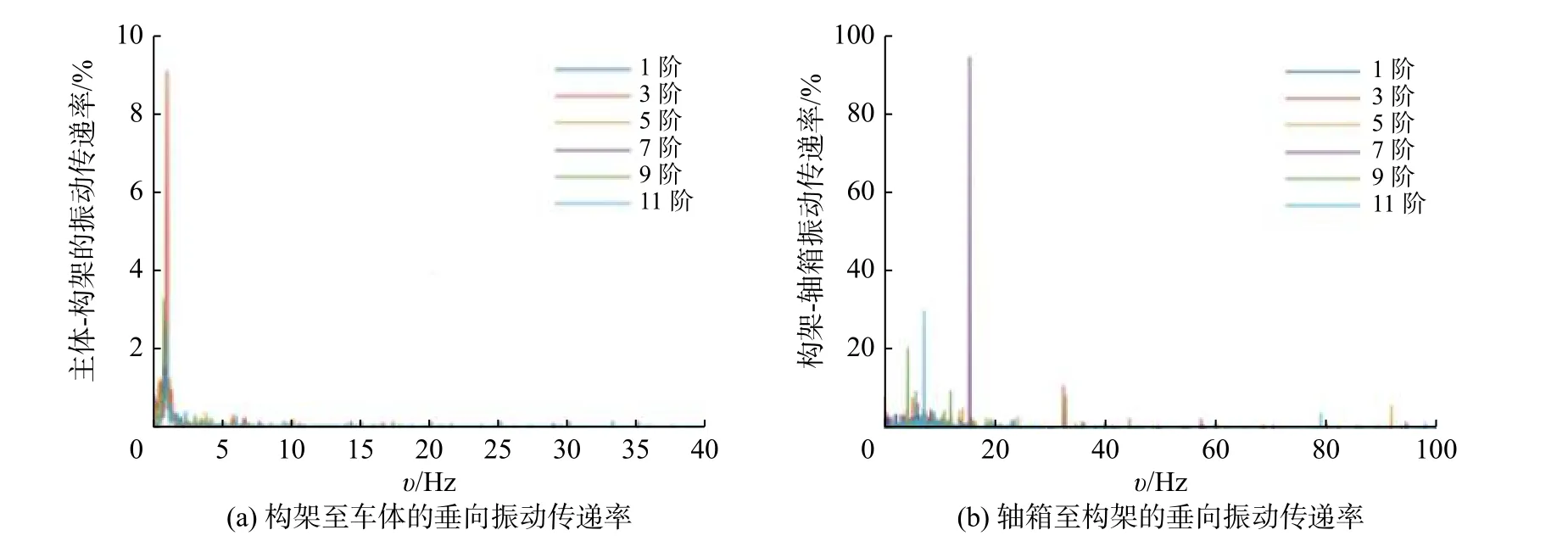
图12 车轮多边形阶数对一系、二系振动传递率的影响Fig.12 Influence of wheel polygon order on vibration transmissibility of primary and secondary suspension
4 结 语
为研究轮轨异常磨耗下的动车组振动特性,参照相关动车组参数建立了车辆-轨道动力学模型,仿真分析了车轮不圆和踏面凹磨的异常磨耗工况的动车组各层级振动响应,结论如下:
(1)随着踏面凹磨的加剧,在动车组各层级中,轴箱的横向振动响应加剧明显,发生转向架横向失稳的概率增加。在频谱分布方面,各层级垂向频谱无明显变化,横向频谱各层级有不同程度右移的趋势,其中转向架横向频谱变化明显。
(2)当车轮多边形阶数从1 变化到11 时,各层级振动响应先加剧后减弱,当阶数为7 附近时,振动响应较为剧烈;各层级振动响应对车轮多边形波深较为敏感,当波深超过2.5 mm 时,仿真结果显示车辆已脱轨。
(3)车轮多边形的阶数和波深变化对垂向振动传递特性影响较小,且频率大于2 Hz 时悬挂系统有效减振,满足人体舒适性的要求。
