车轮多边形对重载机车轮轨相互作用及接触损伤的影响分析

2023-12-21杨云帆王开云

西南交通大学学报 2023年6期

张波，杨云帆，凌亮，王开云

（1.中车株洲电力机车有限公司重载快捷大功率电力机车全国重点实验室，湖南株洲 412001；2.西南交通大学轨道交通运载系统全国重点实验室，四川成都 610031）

重载电力机车具有运量大、成本低和绿色环保等优点，因此，被广泛应用于我国的货物铁路运输.目前我国重载运输系统为满足更高的牵引速度和质量要求，电力机车均装配了大功率牵引电机，同时采用大轴重设计，使得轮轨系统的动态冲击作用更为复杂和恶劣[1].通过大量针对重载机车和线路的现场调研发现，随着服役时间的增长，车轮和钢轨表面的滚动接触疲劳现象日益加剧，而轮轨滚动接触疲劳问题与轮轨系统的动态作用直接相关[2-3].

轮轨表面的轻微滚动接触疲劳问题虽然不会导致脱轨等重大安全问题，但随着疲劳损伤的进一步发展，将会导致车轮和钢轨断裂现象发生，其后果是灾难性的[4].此外，严重的滚动接触疲劳问题也会导致车辆和轨道系统异常振动[5].目前，主要通过车轮镟修和钢轨打磨来消除轮轨表面的滚动接触疲劳损伤缺陷，极大地缩短了车轮和钢轨的使用寿命.

国内外大量研究人员开展了针对车轮和钢轨表面疲劳损伤问题的研究，主要采用实验和理论仿真的方法：Zhao 等[6]利用轮轨滚动接触试验台分析了不同轮轨接触条件和法向载荷工况下的车轮表面疲劳损伤发展规律；Chen 等[7]利用JD-1 试验台分析了车轮扁疤对车轮滚动接触疲劳的影响.研究人员建立了轮轨滚动接触有限元模型来分析不同情况下轮轨表面的疲劳损伤特性：Li 等[8]分析了残余应力对钢轨表面损伤的影响；于荣泉等[9]分析了载荷、车轮缺陷深度和摩擦因数等因素对缺陷附近滚动接触疲劳裂纹发展的影响.大量学者利用车线耦合动力学模型以及基于轮轨系统动力学响应的损伤函数模型或安定理论来定性地分析不同运行工况下轮轨滚动接触疲劳特性[10-12].车轮和钢轨表面的疲劳伤损的发展与磨耗密不可分，Khan 等[13]分析了曲线位置处轨顶摩擦调节器对表面滚动接触疲劳问题的影响.由于不同类型机车牵引拉杆安装方式不同：Liu 等[14]对比分析了不同类型机车车轮踏面的疲劳伤损特性；Lyu等[15]分析了轮径差对机车车轮踏面的疲劳伤损的影响.

通过现场调研发现，车轮多边形广泛存在于机车车轮上[16-17].严重的多边形磨耗无疑会导致剧烈的轮轨垂向冲击作用，但关于车轮多边形磨耗对轮轨切向蠕滑作用及轮轨表面疲劳伤损的影响研究不多[18].本文建立重载列车-轨道三维耦合动力学模型和基于轮轨系统动态响应的损伤预测模型，分析制动工况和轨面变摩擦条件下重载机车车轮多边形对轮轨系统蠕滑作用以及车轮表面磨损的影响规律.

1 数值计算方法

本文基于车辆-轨道耦合动力学理论[19]，建立重载列车-轨道三维耦合动力学模型；基于轮轨系统动态相互作用分析结果，研究车轮多边形磨耗对机车踏面损伤的影响，计算分析流程如图1 所示.

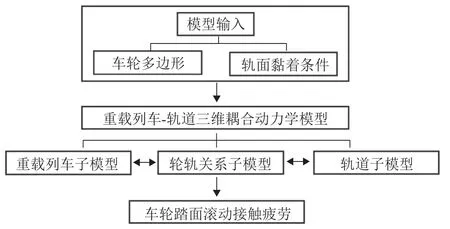
图1 机车车轮踏面滚动接触疲劳仿真流程Fig.1 Simulation flow of wheel-tread RCF of locomotive

1.1 重载列车系统动力学

重载列车系统动力学模型和轨道系统动力学模型是重载列车-轨道三维耦合动力学模型的主要组成部分，如图2 所示.本文重载列车系统动力学模型主要由2 节电力机车和50 节货车组成.由于本文重点关注机车的踏面损伤特性，如若动力学模型计算考虑所有货车的主要部件（包括车体、旁承、侧架和轮对）的空间运动，将会导致计算效率显著降低，因此，在此仅详细考虑机车主要部件的空间运动，采用仅考虑纵向运动的单质点模型模拟货车.

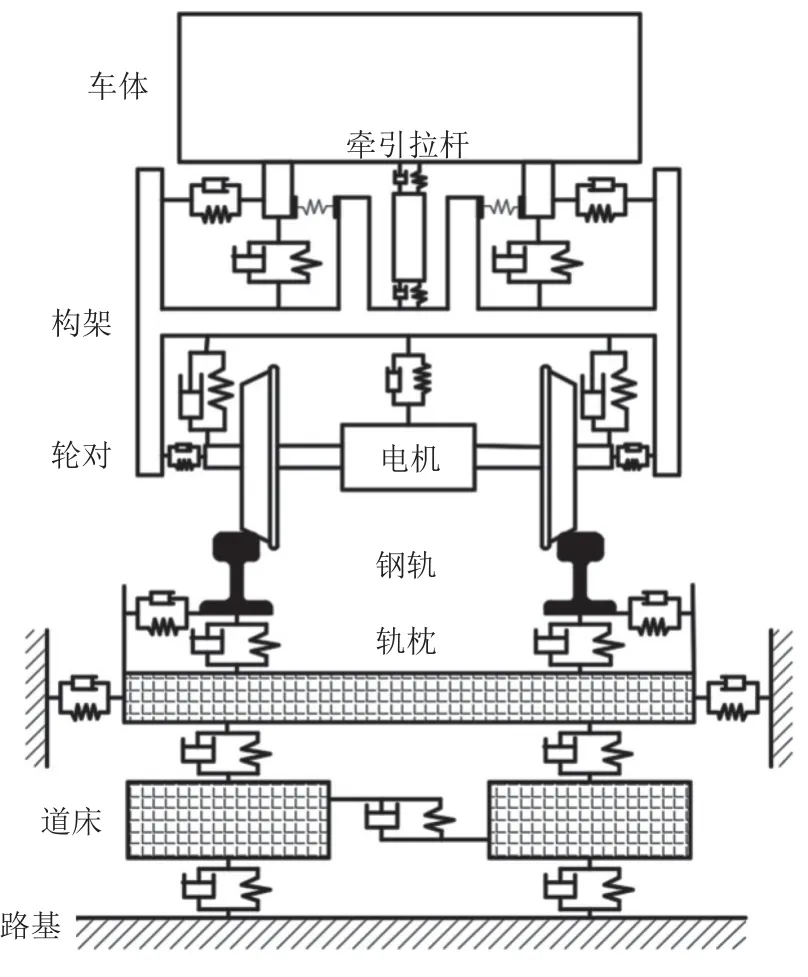
图2 机车车辆-轨道耦合动力学模型Fig.2 Locomotive-track coupled dynamics model

图2 机车主要由车体、牵引拉杆、构架、轮对和电机组成，各个部件通过钢弹簧、油压减振器、橡胶节点和拉杆等悬挂元件约束和固定.本文模型中采用刚性体模型模拟机车部件，其中各个部件考虑纵向、横向、垂向、侧滚、点头和摇头运动自由度.采用具有非线性特性的三维弹簧-阻尼单元模拟悬挂元件.此外利用具有迟滞特性和非线性特性的弹簧-阻尼单元模拟车间钩缓系统[19].

重载电力机车一般配置了防滑控制系统[16]，本文采用比例积分（PI）控制模型来模拟机车的防滑控制器.在此假设：如若轮轨纵向蠕滑率超过了防滑控制器的控制阈值，轮轨防滑控制器则会被触发，此时牵引/制动力矩将会通过控制算法改变，防滑控制器将会提供缩减力矩以防止轮对打滑.

缩减力矩可通过式（1）[20]计算.

式中：sthres为设定的防滑控制阈值，本文设置为0.03，s为轮轨滑行率，P和I为控制系数，t1和t2分别为控制器触发的起始和终止时间，e(t)为实时蠕滑率与设定的防滑控制阈值之间的差值.

重载列车系统的动力学模型[19]为

式中：MHL为列车系统广义质量矩阵，CHL为列车系统广义阻尼矩阵，KHL为列车系统广义刚度矩阵，xHL为列车系统广义位移矢量，FHL为列车系统所受到的外部力载荷矢量.

1.2 轨道系统动力学

轨道系统主要由2 股钢轨、扣件、轨枕、道床和路基组成，采用分层模型模拟轨道系统，忽略路基及以下结构的振动.钢轨振动采用考虑纵向伸缩、垂向和横向弯曲以及扭转振动的离散点支撑梁模型求解，其中垂向和横向弯曲振动采用Euler 梁模拟，梁的边界条件为“简支-简支”；扣件系统采用三维弹簧-阻尼单元模拟；轨枕和道床采用刚性体模拟，考虑其垂向、横向和侧滚振动，轨枕和道床之间以及道床和路基之间的相互作用同样采用弹簧-阻尼单元模拟.

轨道系统的动力学模型[19]为

式中：MHT为轨道系统广义质量矩阵，CHT为轨道系统广义阻尼矩阵，KHT为轨道系统广义刚度矩阵，xHT为列车系统广义位移矢量，FTL为轨道系统所受到的路基作用的外部力载荷矢量.

1.3 轮轨空间相互作用模型

轮轨空间相互作用模型主要包括轮轨空间接触几何、轮轨法向力和轮轨蠕滑力的求解.对于轮轨空间接触几何，采用“迹线法”求解[19]，具体求解过程在此不再复述.

本文考虑轮轨单点接触情况，轮轨法向力Fn采用赫兹接触理论求解，如式（5）[21].

式中：KHertz为赫兹接触刚度；δwr为考虑轮轨接触界面不平顺（包括线路随机不平顺和车轮多边形）的法向压缩量，当法向压缩量小于0 时，意味着此时发生了轮轨分离现象，轮轨法向力为0.

轮轨蠕滑力采用FaStrip 模型[22-23]求解.基于轮轨赫兹接触理论，该模型将轮轨接触斑划分为黏着区和滑动区如式（6），分别对这2 个区域内的切向应力和滑动分布进行求解.

式中：Cp为轮轨接触斑区域；（x,y）为接触斑区域内离散点坐标，∀（x,y）∈Cp；ac和bc分别为椭圆形接触斑的长半轴和短半轴；υ为泊松比；η、ψ和ξ为轮轨蠕滑率因子，可分别由轮轨纵向、横向和自旋蠕滑率求解.

轮轨接触斑内黏着区和滑动区内的切向应力分布求解以及相应的修正方式较为复杂，在此不再复述，具体的推导过程可参照文献[22].轮轨纵向蠕滑力、横向蠕滑力和自旋蠕滑力矩[22]分别为

式中：qx(x,y)为接触斑内纵向切应力分布，qy(x,y)为接触斑内横向切应力分布，A为轮轨接触斑内划分的积分单元面积.

本文蠕滑力求解模型还考虑了复杂轮轨摩擦条件以及轮轨相对滑动量对摩擦系数的影响，该变摩擦系数[23]为

式中：vs为轮轨相对蠕滑速度，B为适用于指数型的摩擦系数衰减系数，μ0和μ∞分别为静摩擦系数和滑动量为无穷大时对应的摩擦系数.

不同轮轨摩擦条件下的求解参数列于表1[23]，表中：KA和KS分别为轮轨接触斑黏着区和滑动区面积缩减系数.考虑轮轨变摩擦系数时，利用赫兹接触理论结合FaStrip 轮轨蠕滑力模型求解不同轮轨摩擦条件和轮轨蠕滑率情况下的轮轨蠕滑特性，如图3 所示（轴重25 t，运行速度70 km/h）.其中，黏着系数定义为纵向蠕滑力除以轮轨法向力.

表1 不同轮轨摩擦条件下接触参数Tab.1 Contact parameters under different wheel-rail friction conditions

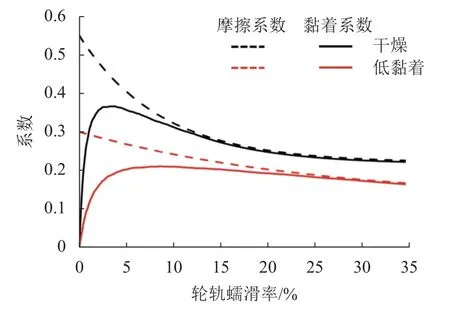
图3 不同接触条件下轮轨黏着特性曲线Fig.3 Wheel-rail adhesion feature curves under different contact conditions

1.4 模型验证

由于轮轨动态相互作用难以通过测试手段获取，尤其是纵向的相互作用，因此，在此将现场测试和利用该模型仿真计算所得的轴箱振动加速度进行对比，以验证所建立三维重载列车-轨道耦合系统动力学模型的准确性.在对轴箱纵向和垂向振动进行动态测试前，对相应车轮的多边形进行了测试；同时在动力学仿真计算中，也采用该车轮多边形以及美国五级谱轨道不平顺作为轮轨不平顺激励.

图4 为车轮多边形测试结果，可看出该车轮存在明显的谐波型非圆化磨耗，其中最大波深约为0.34 mm，主要不平顺波长约为172 mm.图5 为实测和仿真计算的轴箱纵向和垂向振动对比分析结果.通过对比结果可知，实测轴箱纵向和垂向振动加速度幅值略大于仿真计算所得的轴箱纵向和垂向振动加速度，这是由于在动力学仿真模型中未考虑轴箱结构的柔性特性，同时钢轨表面纵向短波不平顺亦未考虑.总体而言，实测和仿真计算所得的轴箱纵向和垂向振动相差不大，本文所建立的动力学仿真模型可用于分析车轮多边形对重载电力机车轮轨动态相互作用和车轮踏面损伤影响的研究.

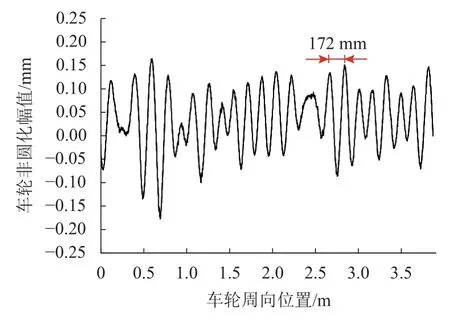
图4 实测车轮多边形Fig.4 Tested wheel polygonal wear

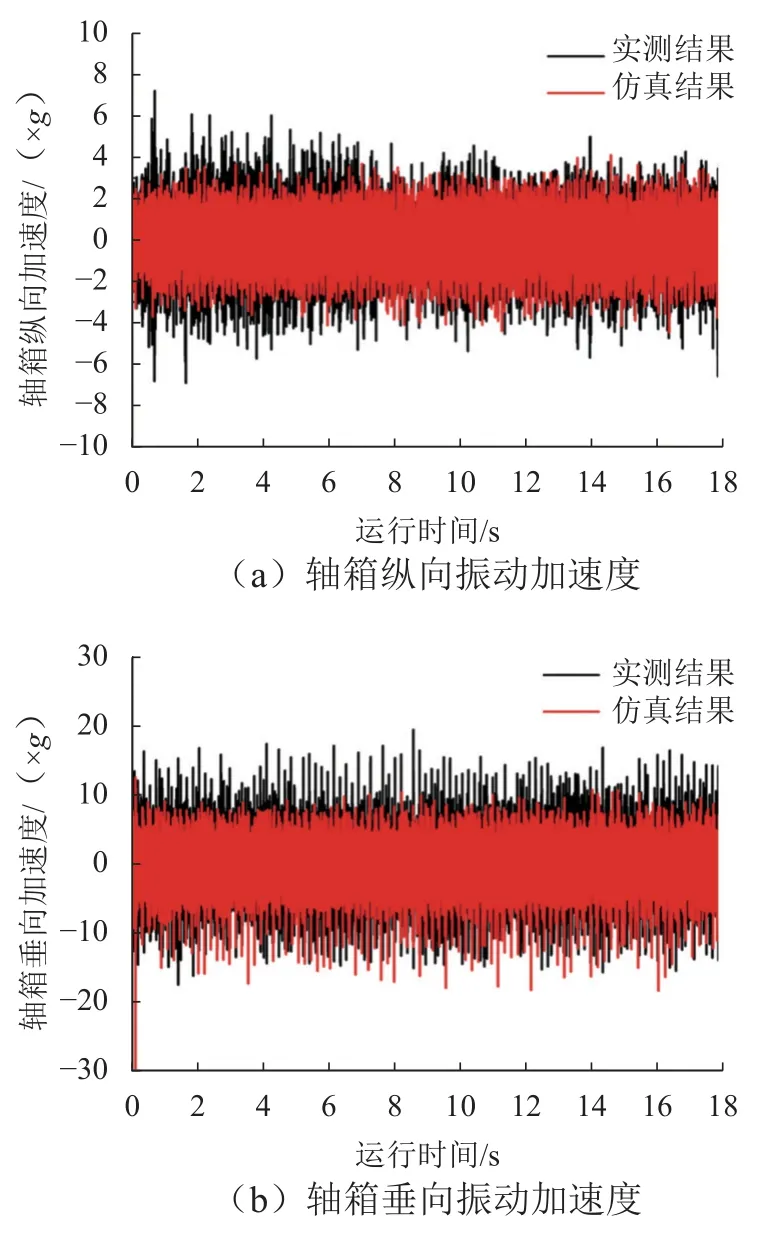
图5 轴箱振动加速度对比分析结果Fig.5 Comparison results of vibration accelerations of the axlebox

2 车轮踏面损伤预测模型

车轮和钢轨踏面的疲劳损伤与轮轨系统动态相互作用密切相关，大量研究人员利用车辆系统动力学仿真计算结果来定性预测不同运行工况下车轮和钢轨踏面的疲劳损伤情况.目前，基于动力学仿真计算的轮轨踏面疲劳损伤预测模型主要有基于赫兹接触模型的损伤函数模型和安定理论[10-12].

安定理论主要利用轮轨蠕滑力和法向力来判断轮轨表面材质是否出现棘轮现象（滚动接触疲劳），但该模型的缺点是无法考虑轮轨蠕滑率以及磨耗对轮轨接触表面疲劳裂纹的影响.损伤函数模型主要利用轮轨蠕滑力和蠕滑率来预测轮轨踏面的滚动接触疲劳，同时考虑了轮轨磨耗和踏面疲劳裂纹的竞争关系.鉴于此，本文利用基于赫兹接触模型和FaStrip 蠕滑模型的损伤函数模型来预测车轮多边形磨耗对车轮踏面损伤的影响.

基于赫兹接触模型和FaStrip 蠕滑模型的轮轨磨耗数分布以及总磨耗数分别为

式中：sx、sy和sφ分别为纵向、横向和自旋蠕滑率.

损伤指数分布和总损伤指数[24]分别为

式中：Ek为损伤指数修正因子，与车轮材料参数和轮轨蠕滑率有关，具体求解方式可参考文献[25].

3 计算结果分析

利用所建立的三维耦合动力学模型和车轮踏面损伤预测模型，分析了制动工况和轮轨表面变摩擦系数条件下，严重的车轮多边形磨耗对不同轮轨接触条件下轮轨动态相互作用和车轮踏面损伤的影响.仿真计算中，严重的车轮多边形如图4 所示，而正常车轮则未考虑车轮多边形磨耗.假设重载列车在直线上运行，初始速度为75 km/h.所施加的制动载荷曲线如图6 所示，当运行至100 m 时开始施加制动载荷.运行线路中，350～750 m 范围内为低黏着接触区域，其余线路则对应于干燥接触区域.采用美国五级谱模拟线路不平顺.限于篇幅，本文仅展示第1 位轮对和第4 位轮对的动态响应分析结果.

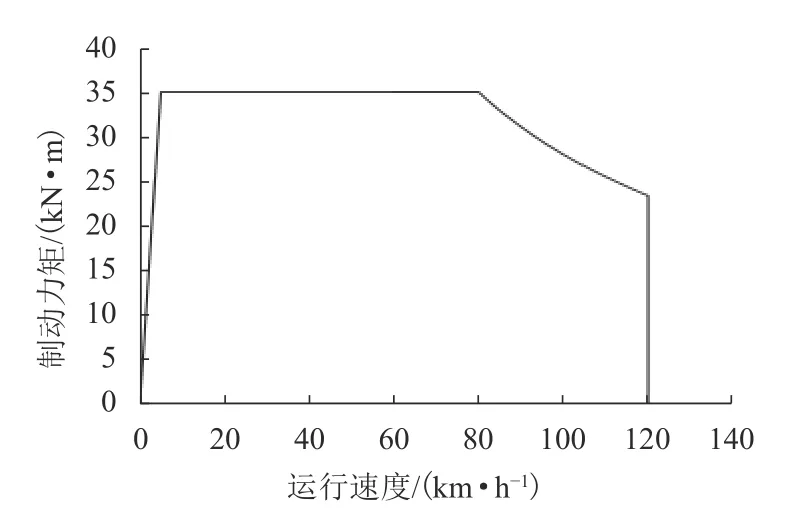
图6 制动力矩Fig.6 Braking torque

图7 为轮轨垂向力动态响应曲线.由图7 可以看出：当车轮存在严重的多边形磨耗时，轮轨垂向力波动明显比正常车轮的轮轨垂向力更为剧烈；施加制动载荷时出现了明显的轴重转移现象，其中干燥接触区域内，第1 位轮对平均增载16.05%，第4 位轮对平均减载16.85%；在低黏着接触区域内，第1 位轮对和第4 位轮对的增载量和减载量分别平均减小4.89%和增大7.78%，这是由于轮轨切向力在低黏着接触条件下减小，从而导致制动工况下的轴重转移量产生相应的改变.

图7 轮轨垂向力Fig.7 Wheel-rail vertical forces

图8 为轮轨纵向蠕滑率动态响应结果.由图8可知：在干燥接触区域内，第4 位轮对的平均轮轨纵向蠕滑率约为0.39%，第1 位轮对的平均轮轨纵向蠕滑率约为0.27%，第4 位轮对的轮轨纵向蠕滑率大于第1 位轮对的轮轨纵向蠕滑率，这是由于在制动工况下，第1 位轮对和第4 位轮对分别增载和减载；在低黏着区域内，轮轨纵向蠕滑率急剧增大，同时防滑控制器被触发，此时第1 位轮对和第4 位轮对的轮轨纵向蠕滑率均维持在控制阈值（3.00%）附近；当车轮存在严重的多边形磨耗时，第1 位轮对的轮轨纵向蠕滑率的波动范围在2.89%～3.25%，略大于正常车轮的轮轨纵向蠕滑率的波动范围2.95%～3.22%，同时，第4 位轮对的轮轨纵向蠕滑率波动范围在2.90%～3.25%，略大于正常车轮的轮轨纵向蠕滑率的波动范围2.99%～3.25%，这是由于车轮多边形磨耗导致了剧烈的轮轨垂向冲击作用，从而使得轮轨切向相互作用产生相应的变化.

图8 轮轨纵向蠕滑率Fig.8 Wheel-rail longitudinal creepage

图9 为轮轨纵向蠕滑力动态响应结果.由图9可以看出：随着制动载荷的增加，第1 位轮对和第4 位轮对的轮轨纵向蠕滑率增大；相比于干燥接触区域，在低黏着接触区域内由于轮轨摩擦系数减小，此时轮轨纵向蠕滑力明显降低，第1 位轮对的平均纵向蠕滑力由干燥接触区域的-31.25 kN 降低到低黏着接触区域的-23.32 kN，第4 位轮对的平均纵向蠕滑力由干燥接触区域的-31.22 kN 下降到-18.18 kN；在制动过程中，当车轮存在严重的多边形磨耗时，轮轨纵向蠕滑力的波动明显较不存在车轮多边形时更为严重，尤其是在低黏着接触区域内，第1 位轮对的轮轨纵向蠕滑力的波动范围较正常车轮的轮轨纵向蠕滑力的波动范围增大4.86 倍，第4 位轮对的轮轨纵向蠕滑力波动范围较正常车轮的轮轨纵向蠕滑力的波动范围增大7.25 倍.

图10、11 分别为第1 位轮对和第4 位轮对的磨耗数动态响应结果、损伤指数动态响应结果.由图10、11 可知：制动工况下车轮踏面的磨耗数和损伤指数均较惰行工况下显著增加；在低黏着接触条件下，第1 位轮对在低黏着接触条件下的平均磨耗数和损伤指数分别是干燥接触条件下的8.05 倍和1.44 倍，第4 位轮对在低黏着接触条件下的平均磨耗数和损伤指数分别是干燥接触条件下的4.50 倍和1.01 倍，磨耗数和损伤指数均远大于干燥接触条件下的磨耗数和损伤指数，这说明低黏着接触条件将会导致更严重的车轮踏面损伤问题；重载列车制动过程中，在干燥接触条件下第1 位轮对的磨耗数和损伤指数均低于第4 位轮对的磨耗数；而在低黏着接触条件下，第1 位轮对的磨耗数明显高于第4 位轮对的磨耗数，而其损伤指数则与第4 位轮对的损伤指数相差不大.

图10 磨耗数Fig.10 Wear number

此外，车轮多边形磨耗对重载机车的车轮磨耗数影响较大.在低黏着接触区域内，当车轮存在严重的多边形磨耗时，第1 位轮对和第4 位轮对的磨耗数波动范围的幅值较正常车轮磨耗数波动范围幅值增大6.44 倍和6.22 倍，磨耗数的波动明显较正常车轮的磨耗数波动更为剧烈.当车轮存在严重的多边形磨耗时，在干燥接触条件下，第1 位轮对和第4 位轮对的损伤指数波动范围幅值较正常车轮损伤指数的波动范围幅值增大19.59%和39.43%，车轮踏面损伤指数也比正常车轮的损伤指数剧烈，但在低黏着接触区域内2 种车轮的损伤指数相差不大.