Wave Radiation by a Floating Body in Water of Finite Depth Using an Exact DtN Boundary Condition

RIM Un-Ryong

Wave Radiation by a Floating Body in Water of Finite Depth Using an Exact DtN Boundary Condition

RIM Un-Ryong*

Institute of Ocean Engineering, Kim Chaek University of Technology, Pyongyang 999093, Democratic People’s Republic of Korea

The present paper focuses on the wave radiation by an oscillating body with six degrees of freedom by using the DtN artifi- cial boundary condition. The artificial boundary is usually selected as a circle or spherical surface to solve various types of fields, such as sound waves or electromagnetic waves, provided that the considered domain is infinite or unbounded in all directions. However, the substantial wave motion is considered in water of finite depth, that is, the fluid domain is bounded vertically but unbounded horizon- tally. Thus, the DtN boundary condition is given on an artificial cylindrical surface, which divides the water domain into an interior andexterior region. The boundary integral equation is adopted to implement the present model. In the case of a floating cylinder, the results of hydrodynamic coefficients of a chamfer box are discussed.

wave radiation; boundary element method; Dirichlet-to-Neumann map; artificial boundary; floating body; finite-depth water

1 Introduction

Ocean wave interactions with floating structures have been of interest in hydrodynamics research for capturing sustainable energy from the sea or protecting the coastal line (Ning, 2018; Deng., 2019). The wave ra- diation from offshore structures floating on the sea is an important area related to this research. Different analyti- cal and numerical methods have been suggested by many researchers to solve the wave radiation problem.

An analytical solution of two-dimensional wave radia- tion by using a small circular cylinder submerged in infi- nite-depth water was suggested by Tyvand (1992), intro- ducing a dimensionless parameter expressed as the radius divided by the submerged depth of the cylinder. The re- sults of hydrodynamic forces and additional mass caused by the oscillating motion of the cylinder showed good performance provided that the dimensionless parameter is smaller than 0.3. Wu (1993) focused on the second-order wave radiation by using a horizontal cylinder under hori- zontal oscillation or circular motion in infinite-depth wa- ter based on the schemes for the wave diffraction problem. Semi-analytical solutions of wave radiation from a verti- cal cylinder in finite-depth water were proposed (Bhatta and Rahman, 2003; Drobyshevski, 2004; Lu and Wang, 2015; Ren, 2018).The water domain is divided into an interior region underneath the cylinder and an exterior one unbounded horizontally. Series-type analytical solu- tions with unknown coefficients for velocity potential are derived for each region, and the coefficients are determined by an algebraic method from matching conditions at the interface between two regions.

Williams and Abul-Azm (1989) studied the approximate analytical solution of the wave radiation from cylinder ar- rays.After obtaining an analytical solution of the velocity potential for an isolated cylinder, the assumption that the distances between the cylinders are larger than the inci- dent wavelength causes the radiated wave to emanate from one cylinder into a plane wave with reference to another cylinder, which makes the solution for the interaction be- tween the two cylinders simple. The analytical solution for wave radiation can also be found in Wu. (2006) for two cylinders only and Siddorn and Eatock Taylor (2008) for multiple cylinders.

Cyclone-anticyclone asymmetry in rotating shallow wa- ter by gravitational wave radiation from a co-rotating vor- tex pair wasfound by Sugimoto(2015), who intro- duced a two-dimensional domain expressed in cylindrical coordinates to compare the analytical results with numeri- cal data for the amplitude of gravitational waves.

The abovementioned analytical methods are only appli- cable to regular-shaped bodies, particularly vertical cylin- ders from their simplification of analytical derivation. Nu- merical methods for dealing with irregular-shaped bodies were reported by Politis(2002), Teng and Eatock Taylor (1995), and Singh and Babarit (2014), who adopted the boundary element method (BEM) for wave diffraction and radiation problems. Setting boundary conditions at po- sitions far from structures is important in applying BEM to the wave-structure interaction. Several ways to solve this problem have been suggested, which can be roughly di- vided into multi-transmitting formula (MTF) by Liao and Wong (1984) and Liao (1996), Higdon-type non-reflectingboundary conditions (NRBCs) by Higdon (1986, 1987) and Dea (2011, 2013), and damping zone method by Shao and Faltinsen (2010). Coupling MTF with the damping zone method was reported by Duan(2015), and Xu and Duan (2013).

Givoli (1992) found an exact NRBC on an artificialboundary to provide a numerical solution for exterior wave problems. The artificial boundary is selected as a circle or sphere to enclose the obstacle; thus, the fluid domain is divided into interior and exterior regions. The boundary condition for the interior region is defined fully after a Dirichlet-to-Neumann (DtN) map on the artificial bound- ary is obtained from the exterior region. Bao and Han (2000) and Premrov and Spacapan (2004) proposed local DtN maps with the finite element method to solve two-dimensional Helmholtz equations. Harwood and Dupère (2015) and Chaillat(2017) adopted BEM with a DtNmap to solve two-dimensional Helmholtz equation andthree-dimensional Navier equation. More studies on DtN maps can also be found in Huang and Yu (2009), and Bar-ucq(2010).

The abovementioned artificial boundaries are selected as a circle in a two-dimensional problem or a spherical sur-face in a three-dimensional problem, provided that the con-sidered domain is infinite or unbounded in all directions, that is,-,-, and-directions. However, the substantial wave motion is considered in water of finite depth, that is, the fluid domain is unbounded horizontally but bounded vertically (, finite in-direction).Recently, Rim (2021) suggested an exact DtN artificial boundary condition to study the three-dimensional wave diffraction by station- ary bodies in water of finite depth, which is the first part of the wave-structure interaction problem.

The present paper focuses on the second part of the wavestructure interaction problem, that is, the wave radiation by an oscillating body with six degrees of freedom by using the DtN boundary condition. The DtN condition is given on an artificial cylindrical surface, which divides the water domain into an interior region and an exterior one. A boundary integral equation (BIE) is constructed to solve the wave radiation problem in the interior region, where theboundary conditions are fully defined by the DtN conditionon the artificial cylindrical surface and traditional boundary conditions on free-water surfaces and seabed.

2 Mathematical Formulation for the Wave Radiation Problem

A body floating on the free-water surface of finite depthis illustrated in Fig.1a. A right-handed Cartesian coor- dinate systemis introduced; thus, theplane is at the free-water surface, and theaxis points upward. As- suming that the isotropic, incompressible, and inviscid fluidis irrotational, the radiation problem can be treated with the fluid motion denoted by the radiated velocity potential

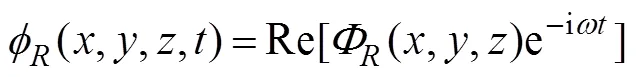
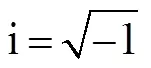
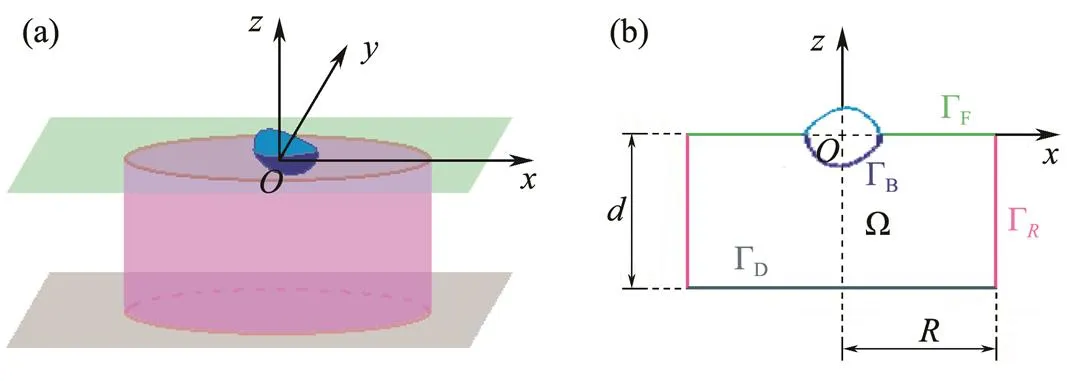
Fig.1 (Colour online) Schematic diagram. (a), bird view ofa mean free surface (top plane with green), a seabed (bot- tom plane with gray), a floating body with blue, and an ar- tificial circular cylindrical surface with rose pink; (b), front view of the interior domain.

In the wave radiation problem, the displacement of the body in the-th mode can be expressed as

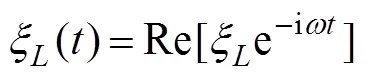
and the spatial potentialcan be decomposed as follows:

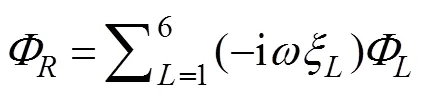
whereis the motion amplitude in the-th mode;=1, 2, ···, 6, corresponding to surge, sway, heave, roll, pitch, and yaw, respectively, andis the complex radiated spa- tial potential caused by the unit amplitude velocity oscil- lation of the body in the-th mode. Moreover, eachsatisfies the governing equation and the following bound- ary conditions:

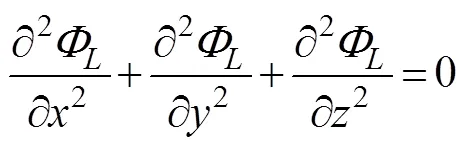
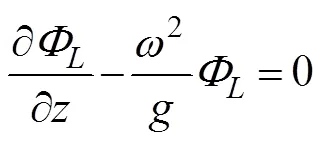
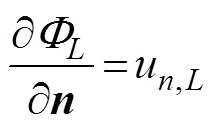
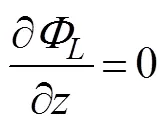
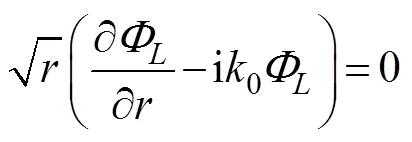
where=(n,n,n) is the unit normal vector directed into the fluid on the wetted surface of the body, andu, Ldenotes the normal component of the velocitycaused by the unit oscillatory motion of the body in the-th mode.Eq.(6) is known as the Sommerfeld radiation condition, where0is the wave number satisfying the following dispersion relation:

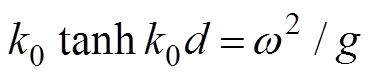
At present, an artificial cylinder with radiusis intro- duced (Fig.1) to solvefor the confined water domain. An artificial cylinder has been selected; thus, the body can be enclosed, and the attentional fluid domain can be in- cluded. Then, the entire fluid domain is divided into a finite interior domain and an infinite exterior domain. The interior fluid domain Ω is enveloped by the artificial sur- face Γ, seabed ΓD, wetted surface of the bodyΓB, and mean free surface ΓF(Fig.1b). The boundary condition on ΓRcan be set as ∂/∂=, whereis the DtN map or DtN operator because it maps the Dirichlet datato the Neumann datum ∂/∂on Γ. The DtN operator reflects anexact boundary condition on the artificial surface.The waveradiation problem in the interior domain can be ex- pressed as follows:

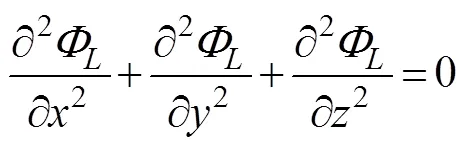
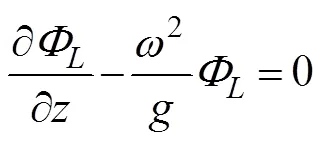
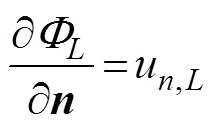
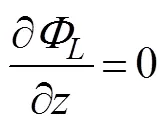
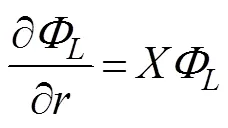
3 Dirichlet-to-Neumann Map

The DtN map on Γcan be obtained by solving the fol- lowing problems in the exterior domain Ωe:

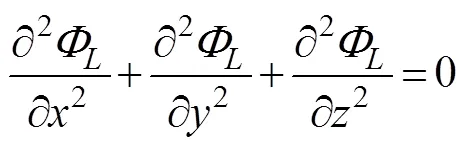
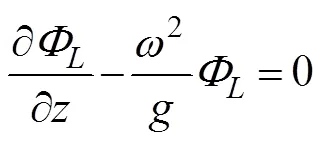
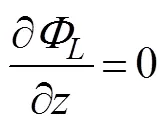
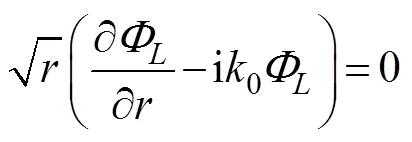
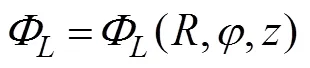
where Eq. (17) is known as the Dirichlet boundary condi- tion, that is, the spatial velocity potential on the artificial surface Γis assumed to be already given as(,,). By separating the variables,a general solution for Eqs. (13)–(16) can be expressed as follows:

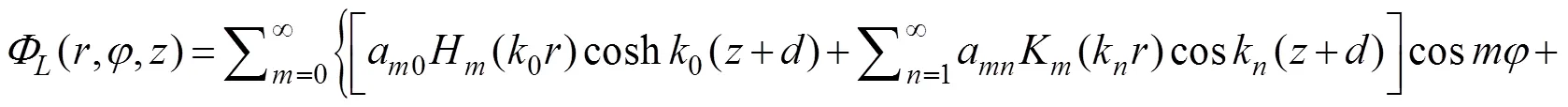
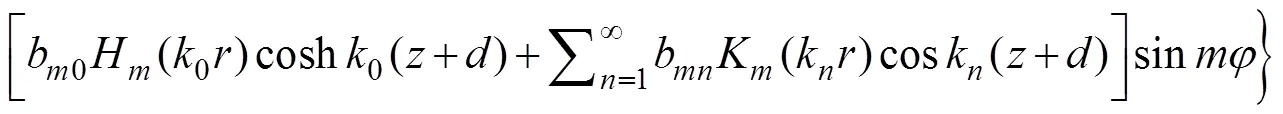
whereaandb(,=0, 1, 2, ···) are unknown con- stants;H(·) is the Hankel function of the first kind of order;K(·) is the modified Bessel function of the sec- ond kind of order, andksatisfies the following rela- tion:

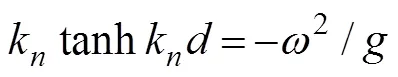
Eq. (18) is a Fourier series for, and each Fourier coef- ficient can be expressed by using the following orthonor- mal set in [−, 0]:

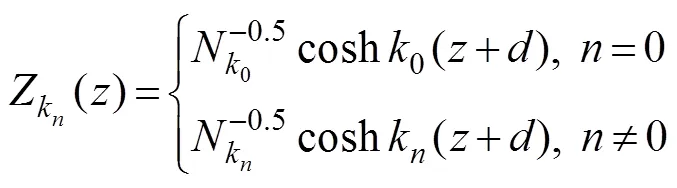
where

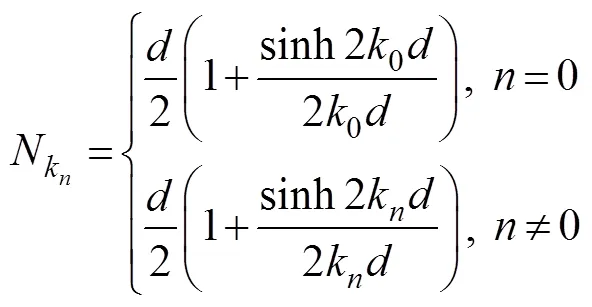
Substituting=into (18) and using the Dirichlet bound- ary condition (17), unknown coefficientsaandbare calculatedas follows:

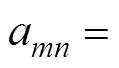
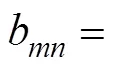
where

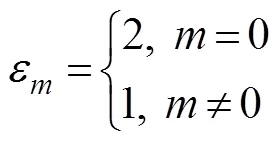
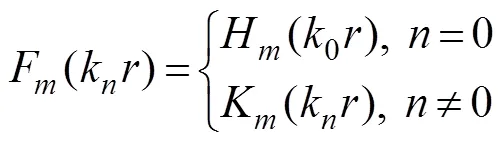
Using the Dirichlet boundary condition on the artificial surface (Γ), Eq. (18) or a solution for the exterior fluid do- main can be expressed as follows:

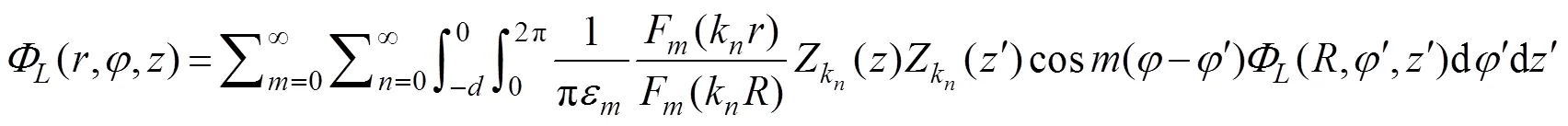
Differentiating Eq. (26) with regard toand setting=, the DtN map on Γis calculated as follows:

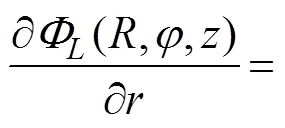
whereχ(,,−) is the DtN kernel presented in the following equation.

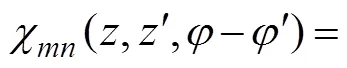
The DtN operatorin Eq. (12) is determined by Eq. (27). Thus, a BIE can be constructed from Eqs. (8)–(12) tosolve the wave radiationproblem for the interior fluid do- main, which will be mentioned in the next section.

4 Implementation by BIE

Based on Green’s second identity, a BIEfor the spatial velocity potentialis written as follows:

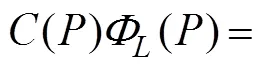
where Γ is the boundary surface of the interior fluid do- mainΩ (, Γ=ΓF+ΓB+ΓD+Γ),andrepresent fieldand source points on Γ, respectively,() is the solid angle at,is the unit normal vector at, and(,) is the following Rankine source Green function:

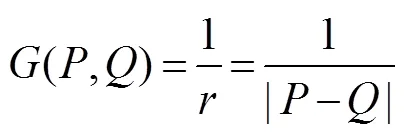
Using the boundary conditions (9)–(12) and (27), Eq. (29) is then rewritten as follows:

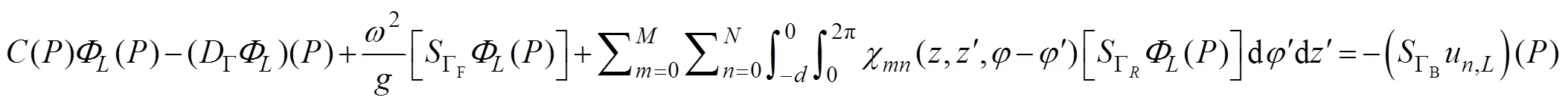
whereandare the operators on an arbitrary bound- arydefined as follows:

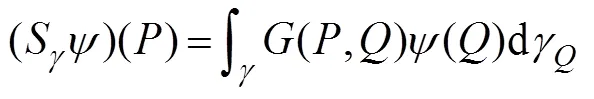
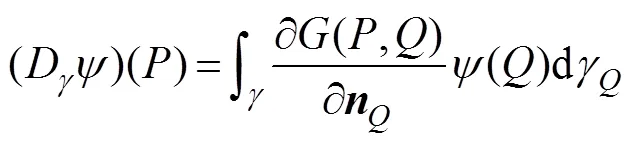
u, Lin the right-hand side of Eq. (31) is already given by the body motion in the-th mode; thus, the unknown radiation potentialin the left-hand side can be deter- minedby discretizing the whole boundary Γ into a finite number of panels and by applying BEM. The detail calcu- lation for each panel can be found in Appendix A of Rim (2021).

5 Results and Discussion

Onceis determined, the radiation force acting on the body in componentis written as

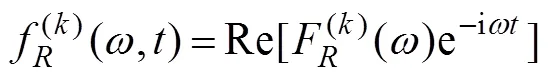
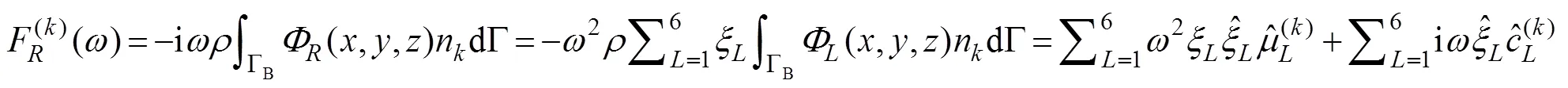
where

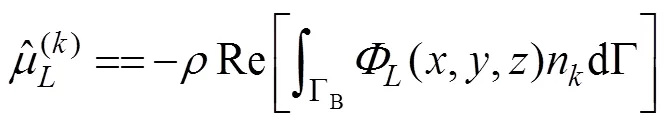
and

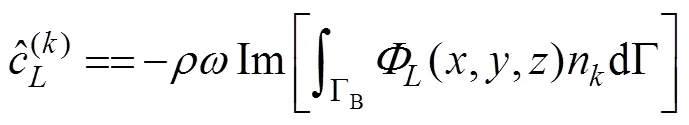
are the added mass and damping coefficient in componentcaused by the unit velocity oscillation motion of the body in the-th mode, in whichnis the-th component of the generalized normal vector expressed as1=n,2=n,3=n,4=−(−0)n+(−0)n,5=(−0)n−(−0)n, and6=−(−0)n+(−0)n.

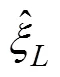
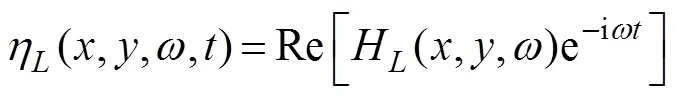
whereH(,,) represents the complex amplitude of the wave elevationat SWL caused by the oscillation of the body in the-th mode, which can be calculated as fol- lows:

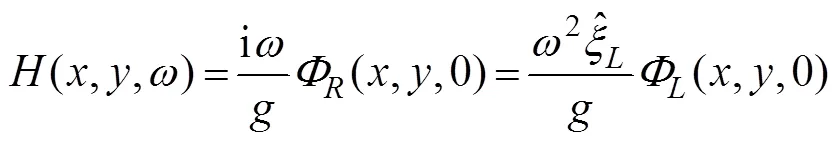
5.1 Model Validation

A cylinder with radiiand draftis selected to validate the present method. In comparing the results, the hydrody- namic coefficients are non-dimensionalized, which are pre- sented as follows:

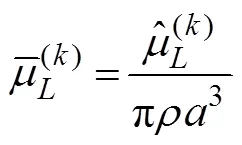
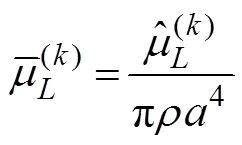
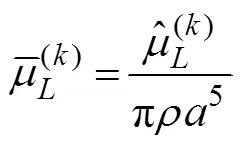
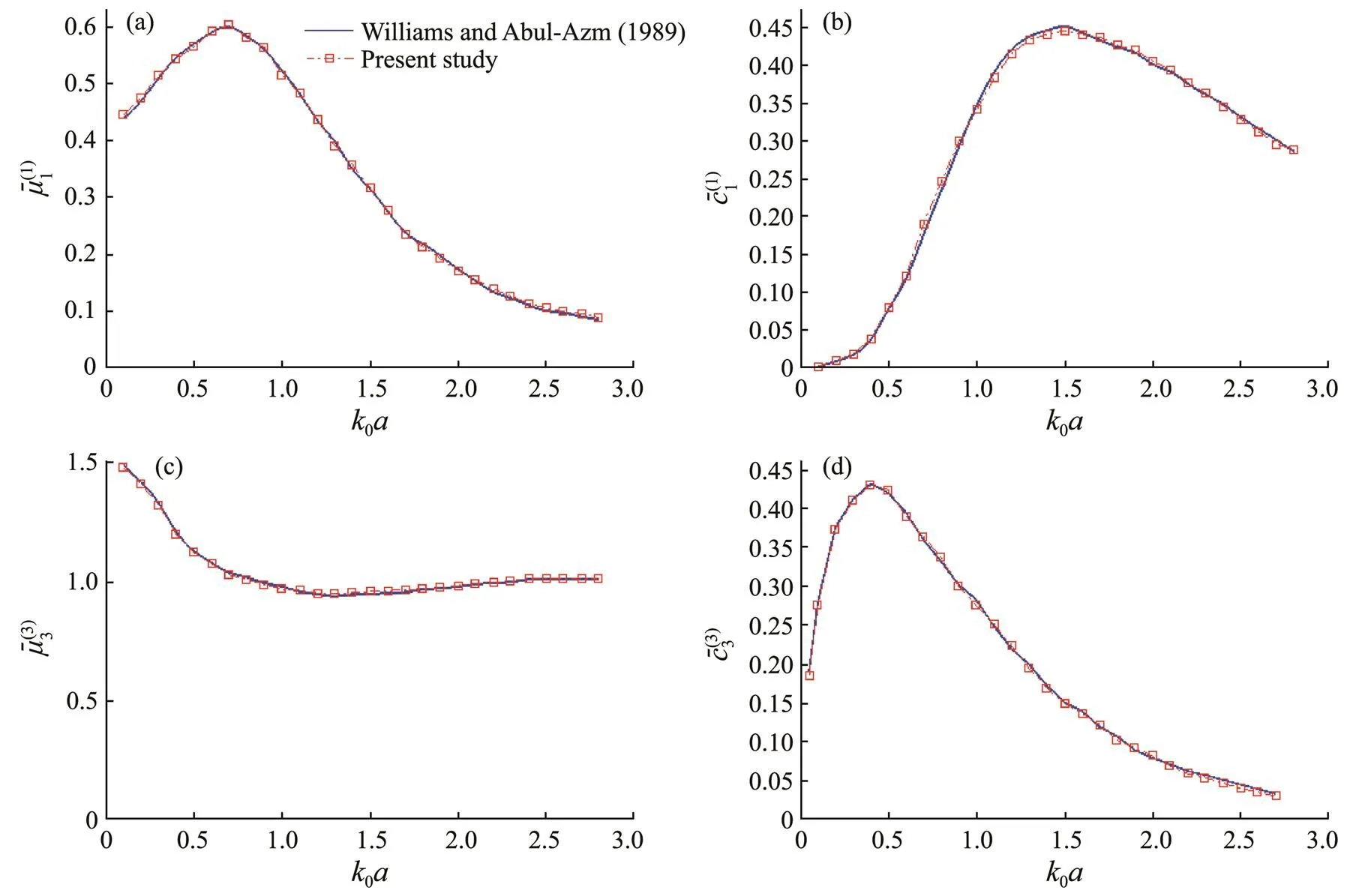
Fig.2 Comparison of the present study with the results of Williams and Abul-Azm (1989) for hydrodynamic coefficients of a cylinder.

5.2 Hydrodynamic Coefficients of a Chamfer Box

The hydrodynamic coefficients of a single chamfer box are estimated for practical purposes. Fig.3(a) shows a sin- gle chamfer box with length (B), width (B), height (B), fillet radius (B), and draft (B). In this case, the non-di- mensionalized hydrodynamic coefficients of the chamfer box are presented as follows:

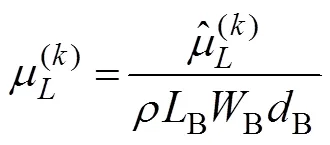
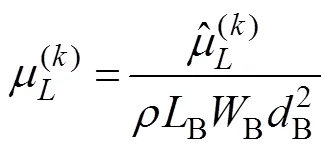
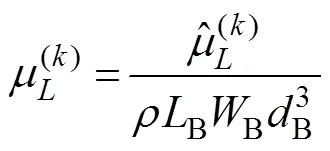
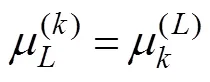
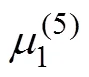
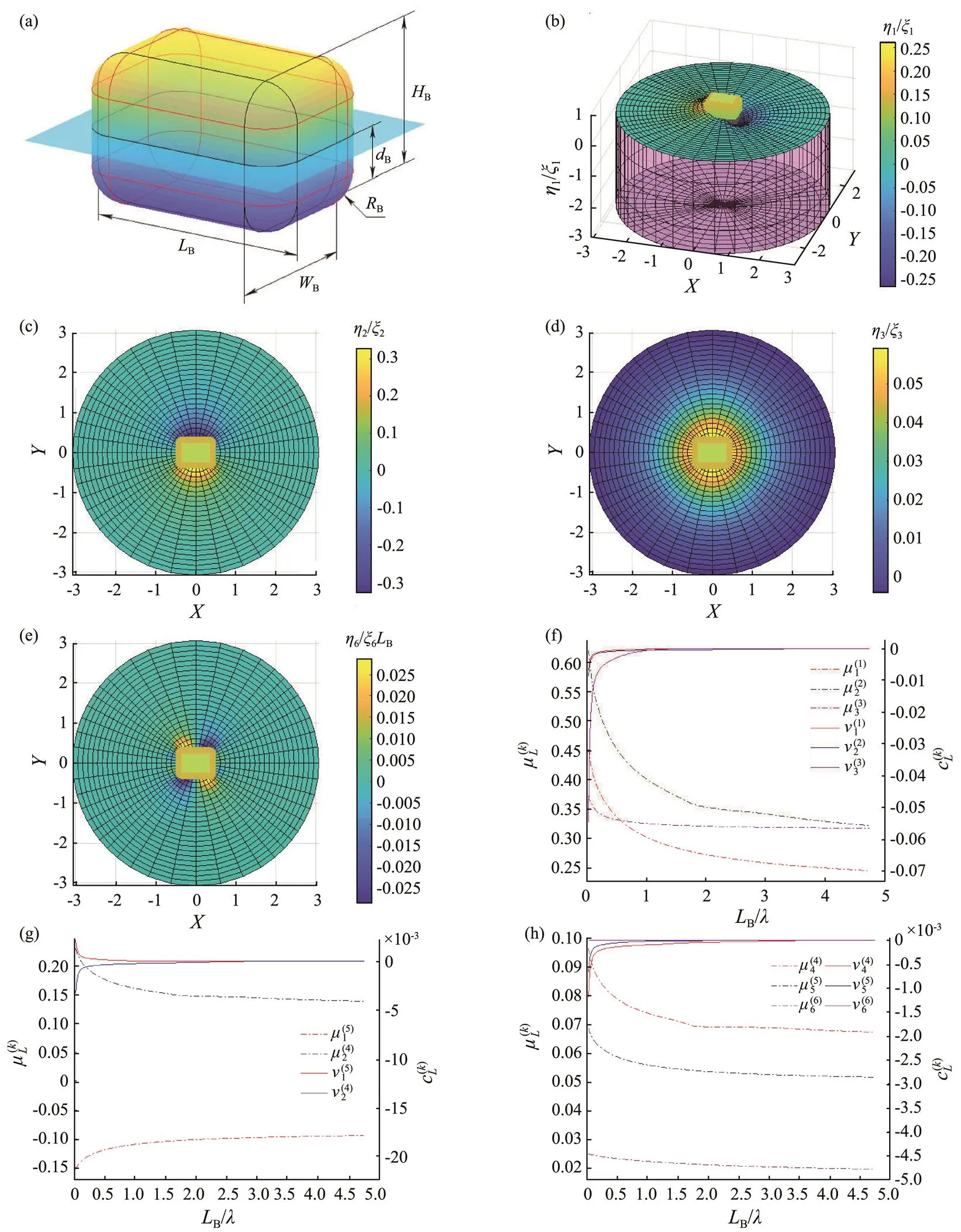
Fig.3 Wave elevation and hydrodynamic coefficients of a floating chamfer box with WB/LB=0.8, dB/LB=0.65, RB/LB=0.15, and d/LB=3: (a), configuration of the chamfer box; (b–e), wave elevation because of the oscillation of the box in the 1st, 2nd, 3rd, and 6th modes, respectively; (f–h), added mass and damping coefficients of the chamfer box.

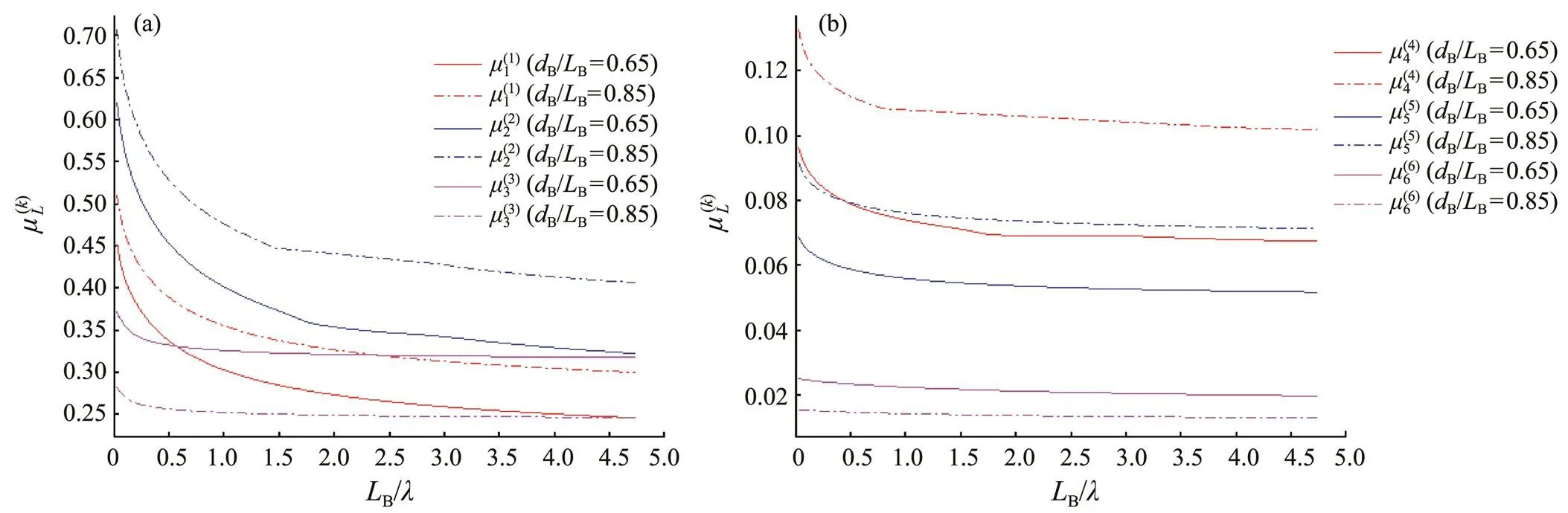
Fig.4 Effect of the draft on the added mass: (a) translation mode and (b) rotation mode.

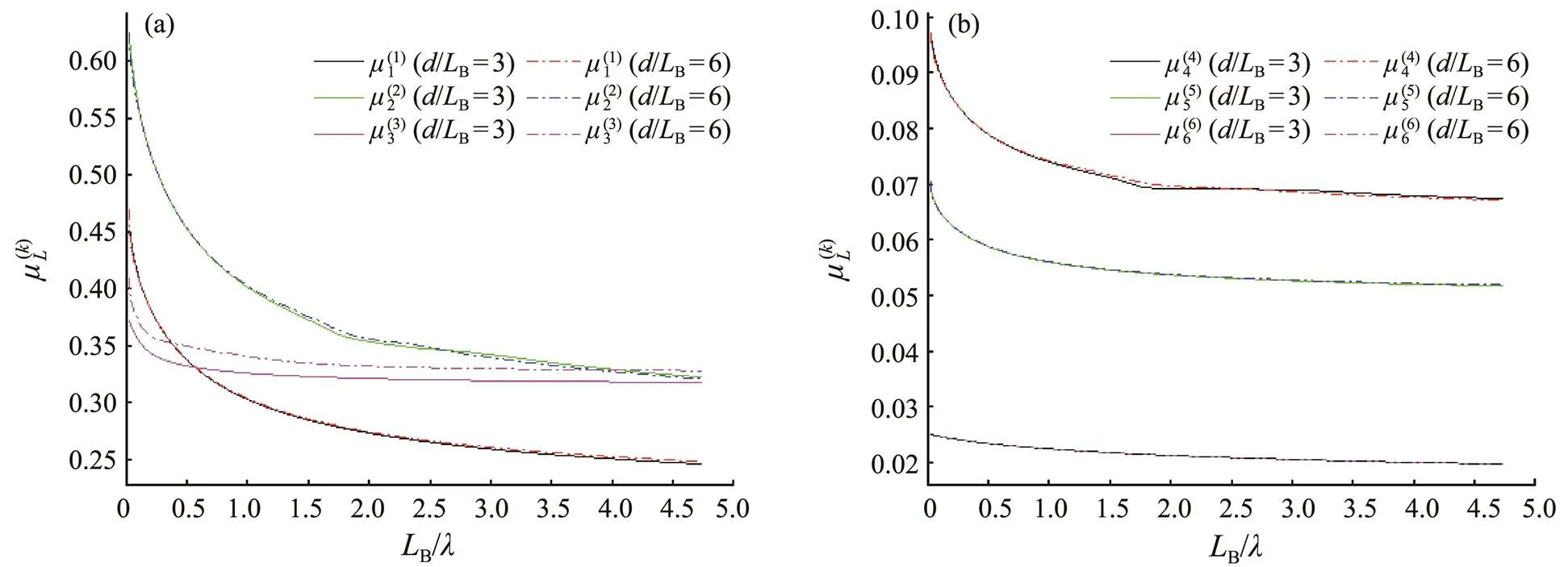
Fig.5 Effect of water depth on the added mass: (a) translation mode and (b) rotation mode.

6 Conclusions

An exact DtN condition for an artificial circular cylin- drical surface is presented to solve the three-dimensional wave radiation by a floating body in finite-depth water with boundary conditions on the free-water surface and seabed. The fluid domain around the body is divided into an interior region and an exterior one by the artificial sur- face. The upper and lower faces of the interior region are parallel, and they have their own boundary conditions (, free surface condition and seabed condition, respectively). Thus, only the additional boundary condition on the inter- face between the two regions is needed to find a solution to the three-dimensional wave radiation problem. DtN map-ping is established only on the artificial cylindrical sur- face, followed by BEM implementation of Laplace’s equa- tion with its full boundary condition. Theintroduction of the DtN artificial boundary converts the horizontally infi- nite water domain into horizontally finite domain with a finite depth, that is, finite volume by the artificial bound- ary, which makes BEM implementation easier than the case of the original water domain because it involves the difficulty of implementing BEM caused bythe horizontal infinityof the original domain.

The present method is verified by using a floating cyl- inder, which shows good consistency with the precedent paper. The hydrodynamic coefficients of a chamfer box are calculated, and their effects on draft and water depth are discussed, which shows that the larger the draft is, the larger the added mass in the horizontal modes but the smaller it is in the vertical mode. In addition, the deeper the water domain is, the larger the added mass is in the heave mode, but a slight difference is observed in other modes. The present model will be applied to assess hydrodynamic coefficients of an arbitrary-shaped floating body.

Bao, W., and Han, H.,2000. High-order local artificial boundary conditions for problems in unbounded domains., 188: 455-471.

Barucq, H., Djellouli, R., and Saint-Guirons, A., 2010. Three-dimensional approximate local DtN boundary conditions for prolate spheroid boundaries., 234: 1810-1816.

Bhatta, D. D., and Rahman, M., 2003. On scattering and radiation problem for a cylinder in water of finite depth., 41: 931-967.

Chaillat, S., Darbas, M., and Louër, F. L., 2017. Fast iterative boundary element methods for high-frequency scattering prob- lems in 3D elastodynamics., 341: 429-446.

Dea, J. R., 2011. Improving the performance of Higdon non-reflecting boundary conditions by using weighted differencing., 61: 1186-1197.

Dea, J. R., 2013. Absorbing boundary conditions for the frac- tional wave equation., 219: 9810-9820.

Deng, Z., Wang, L., Zhao, X., and Huang, Z., 2019. Hydrody- namic performance of a T-shaped floating breakwater., 82: 325-336.

Drobyshevski, Y., 2004. Hydrodynamic coefficients of a floating, truncated vertical cylinder in shallow water.,31: 269-304.

Duan, W. Y., Chen, J. K., and Zhao, B. B., 2015. Second-order Taylor expansion boundary element method for the second-or- der wave diffraction problem., 58: 140-150.

Givoli, D., 1992. A numerical solution procedure for exterior wave problems., 43: 77-84.

Harwood, A. R. G., and Dupère, I. D. J., 2015. Calculation of acoustic Green’s functions using BEM and Dirichlet-to-Neu- mann-type boundary conditions., 39: 4134-4150.

Higdon, R. L., 1986. Absorbing boundary conditions for differ- ence approximations to the multi-dimensional wave equation., 47: 437-459.

Higdon, R. L., 1987. Numerical absorbing boundary conditions for the wave equation., 49: 65-90.

Huang, H., and Yu, D., 2009. The ellipsoid artificial boundary method for three-dimensional unbounded domains., 27: 196-214.

Liao, Z. P., 1996. Extrapolation non-reflecting boundary condi- tions., 24: 117-138.

Liao, Z. P., and Wong, H. L., 1984.A transmitting boundary for the numerical simulation of elastic wave propagation., 3(4): 174-183.

Lu, X., and Wang, K. H., 2015. Modeling a solitary wave inter- action with a fixed floating body using an integrated analyti- cal-numerical approach., 109: 691-704.

Ning, D., Zhou, Y., and Zhang, C., 2018. Hydrodynamic mod- eling of a novel dual-chamber OWC wave energy converter., 78: 180-191.

Politis, C. G., Papalexandris, M. V., and Athanassoulis, G. A., 2002. A boundary integral equation method for oblique water-wave scattering by cylinders governed by the modified Helm- holtz equation., 24: 215-233.

Premrov, M., and Spacapan, I., 2004. Solving exterior problems of wave propagation based on an iterative variation of local DtN operators., 28: 291-304.

Ren, K., Wu, G. X., and Ji, C. Y., 2018.Wave diffraction and ra- diation by a vertical circular cylinder standing in a three-di- mensional polynya., 82: 287-307.

Rim, U. R., 2021. Wave diffraction by floating bodies in water of finite depthusing an exact DtN boundary condition., 239: 109711, https://doi.org/10.1016/j.oceaneng.2021.109711.

Shao, Y. L., and Faltinsen, O. M., 2010. Use of body-fixed co- ordinate system in analysis of weakly nonlinear wave-body problems., 32: 20-33.

Siddorn, P., and Eatock Taylor, R., 2008. Diffraction and inde- pendent radiation by an array of floating cylinders.,35: 1289-1303.

Singh, J., and Babarit, A., 2014. A fast approach coupling Bound- ary Element Method and plane waveapproximation for wave interaction analysis in sparse arrays of waveenergy converters., 85: 12-20.

Sugimoto, N., Ishioka, K., Kobayashi, H., and Shimomura, Y., 2015. Cyclone-anticyclone asymmetry in gravity waveradia- tion from a co-rotating vortex pair inrotating shallow water., 772: 80-106.

Teng, B., and Eatock Taylor, R., 1995. New higher-order boundary element methods for wave diffraction/radiation., 17: 71-77.

Tyvand, P. A., 1992. Wave radiation and diffraction from a small submerged circular cylinder., 9: 279-288.

Williams, A. N., and Abul-Azm, A. G., 1989. Hydrodynamic in- teractions in floating cylinder arrays–II. Wave radiation., 16: 217-263.

Wu, B. J., Zheng, Y. H., You, Y. G., Jie, D. S., and Chen, Y., 2006. On diffraction and radiation problem for two cylinders in water of finite depth., 33: 679-704.

Wu, G. X., 1993. Second-order wave radiation by a submerged horizontal circular cylinder., 15: 293-303.

Xu, G., and Duan, W. Y.,2013. Time-domain simulation of wave-structure interaction based on multi-transmitting formula cou- pled with damping zone method for radiation boundary condition., 42: 136-143.

(February 22, 2022;

September 5, 2022;

September 16, 2022)

© Ocean University of China, Science Press and Springer-Verlag GmbH Germany 2023

. E-mail: lur8971@star-co.net.kp

(Edited by Xie Jun)