函数形式的单调有界原理及其应用
2023-12-19赵霜赵莉莉
赵霜,赵莉莉
函数形式的单调有界原理及其应用
赵霜,赵莉莉
(云南大学 数学与统计学院,云南 昆明 650091)
单调有界原理是判断极限是否存在的重要准则之一,但大多数教材中仅介绍过数列形式的单调有界原理.为了更好地阐述单调有界原理的本质,将单调有界原理推广到函数的形式,利用函数极限、上确界、下确界的定义进行了证明.给出了相应的函数形式单调有界原理的应用实例.
函数极限;单调有界原理;上确界;下确界
判断极限存在的常用准则有两种,分别是夹击准则与单调有界原理.在大多数的数学分析与微积分学教材[1-7]中,分数列极限、自变量趋于固定点时函数极限以及自变量趋于无穷大时函数极限三种情形,对夹击准则进行了介绍,并给出了相应的应用实例, 然而对于单调有界原理只介绍了数列形式的情形.在已有文献中,对单调有界原理的研究,也大多集中在利用该原理证明通项以递推公式形式给出的数列极限的存在性[8-10], 很少有文献介绍函数形式的单调有界原理,以及它们的应用.为更好地阐述数列极限与函数极限之间的异同点,分析单调有界原理的本质,本文将单调有界原理推广到函数的形式,并利用函数形式的单调有界原理,证明了第一类重要极限.

1 函数形式的单调有界原理
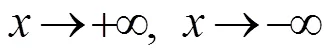
2 函数形式单调有界原理应用实例
[1] 裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,1993:34-41.
[2] 陈传璋,金福临,朱学炎,等.数学分析:下[M].2版.北京:高等教育出版社,1983:43-46.
[3] 张筑生.数学分析新讲[M].北京:北京大学出版社,1991:45-48.
[4] 同济大学应用数学系.高等数学[M].北京:高等教育出版社,2014:43-46.
[5] 四川大学数学系高等数学教研室.高等数学[M].北京:高等教育出版社,1995:45-47.
[6] 华东师范大学数学系.数学分析[M].北京:高等教育出版社,2005:6.
[7] 郑维行,王声望.实变函数与泛函分析概要[M].北京:高等教育出版社,2005:11.
[8] 张留伟.单调有界定理在求递推数列极限的应用[J].广东技术师范学院学报,2016,37(2):1-4.
[9] 谢胜利.平面上的单调有界原理及其应用[J].安徽建筑工业学院学报(自然科学版),2009,17(6):107-109.
[10] 苏柯,孔钰.单调性混合的递归数列求解[J].高等数学研究,2020,23(5):42.
Monotone bounded principle of functional form and its applications
ZHAO Shuang,ZHAO Lili
(School of Mathematics and Statistics,Yunnan University,Kunming 650091,china)
The monotone bounded principle is one of the important criteria for judging the existence of limits,but most textbooks only introduce the monotone bounded principle in the form of series.In order to better explain the nature of monotone bounded principle,the monotone bounded principle is extended to the form of functions,the proof is given by using of the definition of function limit,supremum and infimumthe.Finally,the corresponding application examples of the monotone bounded principle of function form are given.
function limit;monotone bounded principle;supremum;infimum
1007-9831(2023)11-0010-04
O175.1
A
10.3969/j.issn.1007-9831.2023.11.003
2023-03-11
云南省教育厅2020年自然科学基金项目(2020J0020)
赵霜(1999-),女,四川凉山人,在读硕士研究生,从事非线性微分方程研究.E-mail:2368122658@qq.com
赵莉莉(1979-),女,云南大理人,讲师,博士,从事非线性微分方程研究.E-mail:llzhao@ynu.edu.cn
