裂隙粗砂岩渗透率的应力与时间效应研究

韩泽宇, 王 伟, 牛庆合, 杨金鹏, 何卓冉

(1.石家庄铁道大学 土木工程学院,河北 石家庄 050043;2. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043;3.河北省金属矿山安全高效开采技术创新中心,河北 石家庄 050043)

砂岩型铀矿为中国最主要铀资源类型,加大砂岩型铀资源开发力度对促进中国核电发展以及战略核力量具有重大意义。地浸开采是砂岩型铀矿资源的主要开发方式,对铀储层的渗透率要求较高。为了实现砂岩型铀矿高效开采,需对低渗透储层进行改造。已有研究证明,爆破增渗方法可用于低渗透砂岩铀储层改造,并在一定程度上提高了储层渗透率,但该方法的持续性效果尚需进一步研究。储层重构后赋矿层岩体渗透率随应力和时间的演化规律是其涉及的关键科学问题。

相关学者们通过室内实验、分析测试等手段表征了天然裂隙、人造裂隙结构参数,研究了裂隙岩体渗透率演化规律,并构建了相应的理论模型,为裂隙岩体渗流行为的预测奠定了基础。BARTON et al[1]首次发表二维天然裂缝迹线长度的分形测量结果以来,引起了广大学者的关注,自然裂缝模式表现出分形特征天然地质裂隙与统计,为研究裂隙岩石的渗透性提供了一种有效的方法。ANAN et al[2]研究了不同随机粗糙曲面在裂隙法向应力作用下的渗流特性,说明了不同法向应力下裂隙变形特征由裂隙间接触面积决定,同时裂隙由于JRC的增大,隙间涡流的强度与面积也随之增大。李加华等[3]探究了红层砂岩在加载过程中渗透率演化特征,发现砂岩的渗透率随应力增加呈线性降低,孔隙率变化表现出明显的阶段性。核磁共振成像可以显示砂岩内部微孔洞和微裂隙的演化过程,并获得不同应力加载过程砂岩孔隙演化规律。贾群龙等[4]探究了裂隙岩溶介质渗透系数的尺度效应及产生机理,结果表明,随着实验尺度的增大,水平渗透系数也会相应增加,其与渗透系数之间的关系由对数关系转为线性关系,最终渗透系数趋于稳定。王家华等[5]研究了粗糙度和围压对裂隙岩体渗流的影响,并详细阐述了它们对裂隙砂岩中流量的影响机理,表明了导水系数并非定值,其数值随着雷诺数的增大而减小。此外,水力开度随着围压的增大而减小,也将进一步影响渗流特性和动态行为。

在有关理论模型方面上,陶煜等[6]运用单裂隙平行板渗流理论、弹性力学方法,结合模拟电路知识,提出等效渗流阻的概念,在分析裂隙岩体区域中主干裂隙系统几何构造的基础上,建立了基于等效渗流阻的渗流-应力耦合模型。ZHAO et al[7]基于岩石弹性理论和有限差分法,建立煤岩裂隙网络的应力-应变模型,以人工劈裂单裂隙渗流试验参数为依据,用格子玻尔兹曼方法模拟裂隙中的流体流动,研究应力、裂隙密度、裂隙表面粗糙度与孔径对渗流特性的影响。XIAO et al[8]分析了渗流条件下红砂岩破坏过程中强度、变形与渗透率的变化规律,并建立了渗透率与应力的分段函数模型。WANG et al[9]根据中国三峡工程现场勘察,将岩石裂缝几何参数通过离散元法(DEM)生成了一系列计算等效渗透率的二维离散断裂网络(DFN)模型,当正方形模型边长大于40 m时,平行于正方形4条边方向的渗透率基本达到稳定,并以长作为大尺度模拟的REV单元。王俊奇等[10]基于广义达西定律,提出一种新型空间一维环单元模型来计算三维裂隙岩体的渗透张量,简化了以往复杂的三维面状流模型。为验证该模型在计算渗透性方面的可靠性,采用了解析法和数值模拟法进行模型测试,并利用面单元模型对该模型的精度进行校核。

综上所述,尽管前人已进行了大量的探索,但针对原位地层条件下储层改造后裂隙岩体渗透率长时间演化规律的研究尚不充分。为此,通过对含单裂隙粗砂岩和含多裂隙粗砂岩在不同应力和时间影响情况下进行室内渗透率的测量,进而研究渗透率的演化规律,并且对试验数据进行拟合,以期能为今后的岩体工程建设提供参考。

1 砂岩渗流试验研究

1.1 试样准备

试验采用标准圆柱体试样(直径50 mm、长度100 mm)。为了避免试样非均质性对测试结果的影响,所用试样均采自同一岩层,且不含原生裂隙。同时,为了保证测试结果的准确性和可靠性,筛选声波波速相差在5%之内的试样开展研究。

含单裂隙粗砂岩试样是通过人工剪切造缝的方法来制备,CT扫描图见图1(a)。含多裂隙试样则是采用SHPB试验系统来制备动荷载下的含多裂隙粗砂岩试样,CT扫描图见图1(b)。

图1 单裂隙试样和多裂隙试样图

图2 岩石三轴多场耦合试验系统

1.2 试验仪器

试验采用室内岩石三轴多场耦合试验系统。该系统主要由控制及数据采集系统、样品室、温控系统、轴压/围压加载系统和注液系统组成。该系统最大围压和孔压为60 MPa(精度为0.01 MPa),最大轴压为1 000 MPa(精度为0.1 MPa),最高温度为150 ℃(精度为0.1 ℃)。试验装置见图2。

1.3 试验步骤及计算方法

具体试验步骤如下:

(1)启动岩石三轴多场耦合试验系统后,预热处理约0.5 h,以确保设备的运行稳定性和试验结果的精度和可靠性。

(2)用热缩管包裹试样,将试样安装至样品仓。

(3)为了防止液压油渗入试样内部,使用橡胶管和金属箍环对试样进行密封。

(4)将围压腔体移动至底座相应位置,放置围压腔体并拧紧腔体外围螺丝。

(5)打开轴压和围压的低压和高压阀门,同时打开溢油阀和电机,等待试验设备内部的油液充满腔体,直到围压溢油管路中的油排完,说明围压、轴压腔体内的油已充满。

(6)关闭试验设备中的充油按钮、电机旋钮以及围压腔体内的溢油阀门、低压和高压阀门。

(7)分别以3 mL/s和1 mL/s的流量缓慢加载轴压和围压至8 MPa和6 MPa。

(8)待围压和轴压加载好之后加载孔压至2 MPa,同时开始第1组渗透率测量。

(9)按照试验方案,重复步骤(7)、(8),调整轴压和围压,测试下一组渗透率。

渗透率计算基于稳态法。通过给试样两端施加一个稳定的渗透压差,通过测量单位时间内通过岩体的流量来获得试样的渗透率[11]。

(1)

式中,k为渗透率;Q为单位时间流量;A为过水断面面积;ΔP为上下游压差;L为渗流路径长度;μ为水的动力黏度。

1.4 试验方案

1.4.1 渗流-应力试验方案

为了研究改造后赋矿层条件下渗透率演化规律,本次试验考虑轴压、孔压和围压对试样渗透率的影响,具体试验方案见表1。按照该方案首先进行单裂隙试样渗透率测试,其次开展含多裂隙试样渗透率测试。

表1 裂隙试样渗流-应力试验方案 MPa

为了分析轴压、围压和孔压对试样渗透率的影响程度,引入了渗透率应力敏感性系数和渗透率相对变化幅度。

渗透率应力敏感性系数[12]为

(2)

式中,C为渗透率应力敏感性系数;kn第n应力状态下的渗透率,对应的C分别为轴压、孔压与围压的渗透率敏感性系数;kn+i+1为第n+i+1应力状态下的渗透率;σn+i+1为第n+i+1应力;σn+1为第n+1应力。

渗透率相对变化幅度[13]为

(3)

式中,ku为渗透率相对变化幅度。

1.4.2 渗透率-时间效应试验方案

为了能够更真实地模拟地质条件下的岩石变形过程,提高试验结果的可靠性和适用性,该试验中应力采用地下800 m深度的应力状态[14],即轴压为21.6 MPa、围压为17.05 MPa,孔压为2 MPa。

渗透率-时间效应试验时间均为168 h。0～12 h内,以每2 h的时间间隔对试样进行渗透率测量,之后由于渗透率变化过小,以每12 h的时间间隔对试样进行渗透率测量。

2 分析与讨论

2.1 轴压影响下单裂隙粗砂岩和多裂隙粗砂岩渗透率演化规律

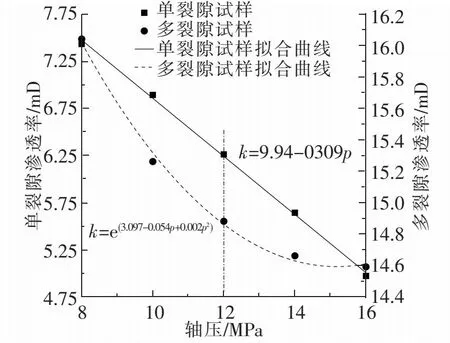
图3 试样渗透率随轴压变化规律及拟合公式曲线图

试样渗透率随轴压演化关系见图3。试验中孔压为2 MPa,围压为6 MPa,随着轴压从8 MPa增加至16 MPa。单裂隙试样渗透率呈线性下降,渗透率从7.43 mD下降到4.97 mD;多裂隙试样渗透率则呈指数型下降,渗透率从16.04 mD下降到14.59 mD。其中含单裂隙试样的渗透率变化幅度为-7.3%、-9.1%、-9.9%、-11.9%,多裂隙试样的渗透率变化幅度为-4.9%、-2.5%、-1.5%、-0.5%。根据渗透率对比得出,在轴压影响下,多裂隙试样的渗透率高于单裂隙试样的渗透率。

由于多裂隙试样中的裂隙渗透率通道数量较多,因此该试样拥有更高的渗透率。在轴压为12～16 MPa之间,多裂隙试样的渗透率变化趋势相较于单裂隙试样更加平缓,这种现象是因为当多裂隙试样的裂缝宽度达到一定程度时,由于法向方向上的应力限制,裂缝无法再继续扩张,因此渗透率变化也会逐渐变得平缓。

单裂隙渗透率轴压敏感性系数分别为0.036、0.042、0.043、0.045,多裂隙渗透率轴压敏感性系数分别为0.024、0.018、0.007、0.002。根据轴压敏感性系数得出,单裂隙试样对轴压的敏感程度明显高于多裂隙试样,且随着轴压的增大,单裂隙试样的敏感性系数逐渐升高,多裂隙试样的敏感性系数逐渐降低。这是因为多裂隙试样的裂隙空间更为复杂,裂隙之间的连通性较差,导致试样的敏感性相对较小。

2.2 孔压影响下单裂隙粗砂岩和多裂隙粗砂岩渗透率演化规律

图4 试样渗透率随孔压变化规律及拟合公式曲线图

试样渗透率随孔压演化关系见图4。此时试验中轴压为16 MPa,围压为6 MPa,随着孔压从2 MPa增加至4 MPa,单裂隙试样呈线型上升,渗透率从4.97 mD上升到6.40 mD;多裂隙试样则呈指数型上升,渗透率从14.57 mD上升到16.68 mD。其中单裂隙试样渗透率相对变化幅度分别为5.2%、5.5%、5.4%、10.0%,多裂隙试样渗透率相对变化幅度分别为0.5%、2.0%、3.2%、8.7%。通过对比2个试样在孔压影响下的渗透率,得出多裂隙试样的渗透率高于单裂隙试样的渗透率。此外,随着孔压的增加,单裂隙试样和多裂隙试样的渗透率会先缓慢增加,然后迅速增加。

在孔压的影响下,单裂隙试样渗透率变化趋势主要与以下2个方面相关。就孔隙结构变化而言,当孔压为2～3 MPa之间,单裂隙试样中的孔隙接近或被完全压实,再施加更高的孔压时,这些裂隙有可能重新打开,导致渗透率急剧增加。从流体流动变化来看,一旦孔隙中的水压力达到一定程度,局部断层和涡流就会形成,这也会导致渗透率突然增加。

就多裂隙试样而言,孔压从2 MPa加载至3 MPa过程中,多裂隙试样的渗透率变化幅度较小。其原因在于此时的孔压仍处于较小值,并未完全打通多裂隙试样中的渗流通道。孔压从3 MPa加载至4 MPa过程中,随着孔压的增大,原本被抑制压实的裂隙面逐渐张开,渗流吼道也逐渐畅通,水通过裂隙的能力也逐渐增强,因此试样渗透率呈现上升的趋势,且上升幅度逐渐增大。

单裂隙渗透率孔压敏感性系数为0.105、0.117、0.121、0.233,多裂隙渗透率孔压敏感性系数为0.003、0.040、0.066、0.184。由孔压敏感性系数得出,多裂隙试样对孔压的敏感程度低于单裂隙试样。随着孔压的增加,2个试样的渗透率应力敏感性系数呈现出先缓慢增大后快速增大的变化趋势。

2.3 围压影响下单裂隙粗砂岩和多裂隙粗砂岩渗透率演化规律

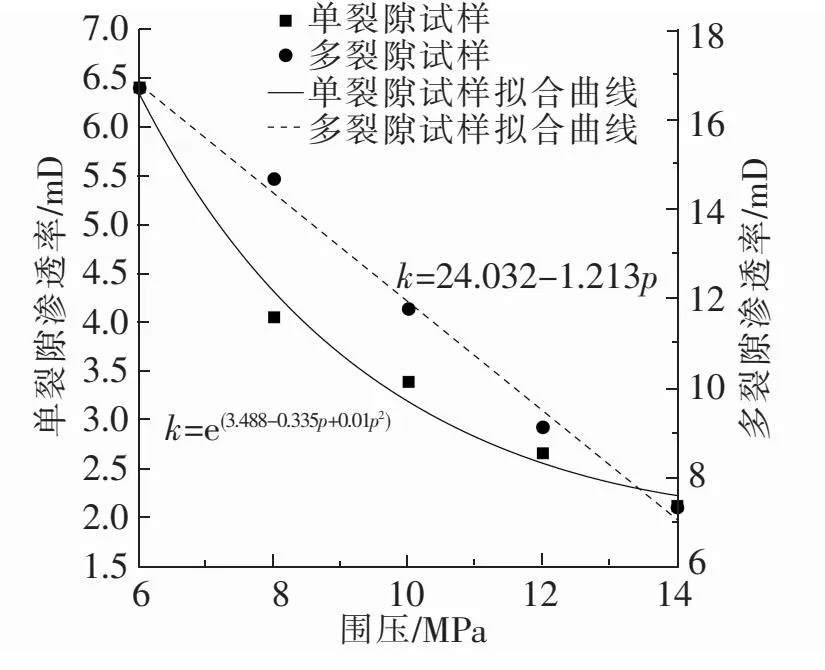
图5 试样渗透率随围压变化规律及拟合公式曲线图

试样渗透率随围压演化关系见图5。试验中轴压为16 MPa,孔压为4 MPa,随着围压从6 MPa增加至14 MPa,单裂隙试样呈指数型下降,渗透率从6.40 mD下降到2.12 mD;多裂隙试样则呈直线型下降,渗透率从16.68 mD下降到7.32 mD。单裂隙试样渗透率相对变化幅度分别为-36.7%、-16.3%、-21.5%、-20.3%,多裂隙试样渗透率相对变化幅度分别为-12.2%、-19.8%、-22.5%、-19.6%。在围压影响下,通过比较2种试样的渗透率得知,多裂隙试样的渗透率高于单裂隙试样的渗透率。其中单裂隙试样随着围压的增加,渗透率呈现先显著降低后缓慢降低的趋势;多裂隙试样的渗透率则呈现下降趋势,其渗透率变化幅度先上升后下降。

2个裂隙试样随着围压的增加,其渗透率均呈现下降的趋势。这是由于随着有效围压不断增大,裂隙中一些支撑作用的隆起和锯齿被挤压甚至碾碎,使得裂隙接触面积逐渐增大。岩屑也会因此脱落,并随着流体移动发生堆积现象,进而导致裂隙渗流通道的截面变小,使得阻渗能力逐渐增大,从而导致渗透率进一步减小[15]。而多裂隙粗砂岩中存在更多的小裂隙和孔隙,这些小裂隙和孔隙能够提供更多的渗流通道。单裂隙试样只有一个裂缝,因此当围压增加时,单裂隙试样的裂隙会更有效地闭合,使得单裂隙试样的渗透率下降更快。

单裂隙渗透率围压敏感性系数分别为0.184、0.052、0.057、0.042,多裂隙渗透率围压敏感性系数分别为0.061、0.087、0.079、0.054。根据围压敏感性系数得知,与多裂隙试样相比,单裂隙试样对围压更为敏感。随着围压的增加,单裂隙试样的敏感性系数先迅速降低,然后缓慢下降;而多裂隙试样的敏感性系数则是先上升后下降。

2.4 砂岩渗透-时间试验

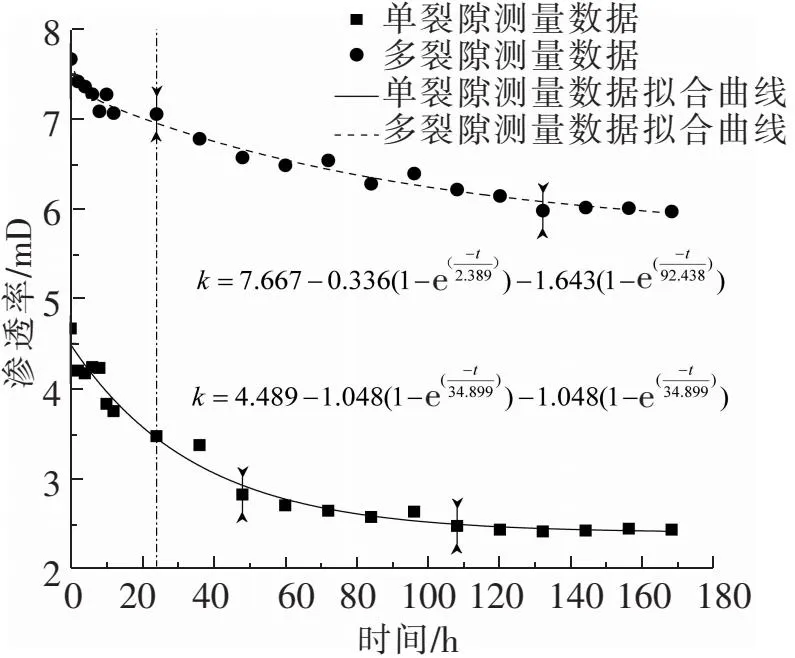
图6 裂隙粗砂岩渗透率随时间演化试验值及拟合公式曲线图

采用对单裂隙粗砂岩和多裂隙粗砂岩渗透率变化的时间效应进行研究,单裂隙试样和多裂隙试样的渗透率随时间演化见图6。在整个试验过程中,多裂隙试样的渗透率始终高于单裂隙试样渗透率。单裂隙试样和多裂隙试样测量数据拟合曲线为指数型曲线,相关系数均为0.98,与测量数据拟合良好。单裂隙试样渗透率随时间演化主要呈3个阶段,在第1阶段(前48 h),渗透率快速降低;在第2阶段(48～108 h),渗透率缓慢降低;第3阶段到了108 h之后,渗透率趋于稳定。以试验开始时的渗透率测试值为基准,试验结果显示,在第1阶段末尾,试样的渗透率减少幅度达到了40%;在第2阶段末尾,减少幅度达到了47%;在整个试验过程中,渗透率减少幅度达到了48%。这说明单裂隙试样的渗透性能受时间因素的影响较大,并且其渗透率随着时间的推移而不断降低。

多裂隙试样渗透率随时间变化也可以分为3段。第1阶段:0～24 h,渗透率降低较快,在第24 h渗透率降低幅度为8%;第2阶段:24～132 h,渗透率降低缓慢,在第132 h渗透率降低幅度为22%;第3阶段:132～168 h,渗透率趋于稳定,最终渗透率降低幅度为22%。

在试验前24 h内,单裂隙试样的渗透率下降幅度大于多裂隙试样。其主要原因是制造多裂隙试样时采用的SHPB方法未能生成完全贯通的裂隙结构,导致填充物大量存在于多裂隙试样中,影响了试样的渗透性能。相比之下,单裂隙试样中的裂隙结构更加贯通,因此在24 h内其渗透率的变化幅度更大。随着时间的推移,2种裂隙试样的渗流通道变形逐渐稳定,渗透率变化幅度低于1%,因此试样的渗透率趋于稳定。

3 结论

分别对单裂隙粗砂岩和多裂隙粗砂岩进行渗流-应力和渗流-时间试验,对比了2种裂隙粗砂岩的渗透率变化。研究了2种裂隙粗砂岩的渗透率随轴压、孔压、围压和时间的演化规律,并通过渗透率应力敏感性公式讨论了轴压、孔压和围压对渗透率影响的大小。主要结论如下:

(1)多裂隙粗砂岩无论在应力还是时间的影响下,其渗透率均高于单裂隙粗砂岩渗透率,但多裂隙粗砂岩的渗透率应力敏感性系数低于单裂隙粗砂岩的渗透率应力敏感性系数,且同一种类型的裂隙粗砂岩渗透率应力敏感性系数存在孔压>围压>轴压这一关系。

(2)单裂隙粗砂岩受到不同应力条件的影响,其渗透率随轴压增大而降低,随孔压增大先缓慢增加后迅速增加,随围压增大先显著降低后缓慢降低;单裂隙粗砂岩的渗透率应力敏感性系数会随轴压的增加而增大,随孔压增加先缓慢增大后快速增大,随围压增加先快速降低然后缓慢降低。

(3)多裂隙粗砂岩受到不同应力条件的影响,其渗透率随轴压增大先快速降低后缓慢降低,随孔压增加先缓慢增加后迅速增加,随围压增大而降低;多裂隙粗砂岩的渗透率应力敏感性系数随轴压增加而降低,随孔压增加先缓慢增大后快速增大,随着围压增加先上升后下降。

(4)在渗流-时间试验中,多裂隙试样的渗透率始终高于单裂隙试样渗透率。而单裂隙粗砂岩和多裂隙粗砂岩的渗透率随时间演化主要呈3个阶段,第1阶段渗透率快速降低,第2阶段缓慢降低,第3阶段趋于稳定。在试验开始的24 h内,单裂隙粗砂岩的渗透率降低幅度比多裂隙粗砂岩大。之后随着时间的变化,2种粗砂岩的渗透率逐渐稳定。