如何在小学渗透计数方法

陈小玲

【摘 要】计数原理作为概念，对小学生而言，抽象、晦涩。而作为排列组合最基本的思想方法，教学中有必要通过“搭配”活动，引导学生感悟有序枚举，进而将计数原理的应用渗透到学生的日常生活中。

【关键词】计数原理 加法原理 乘法原理

计数原理作为排列组合最基本的思想方法，分为“加法原理”和“乘法原理”。计数原理的概念，对于小学低年级的学生而言，较为抽象且难以理解，因此曹培英教授认为“就知识而言，只是渗透与孕伏”。

如何让小学生理解这两个基本原理呢？在北师大版数学三年级上册“搭配中的学问”中有涉及。本课的核心问题是小丑的服装搭配问题，即小丑有2顶帽子和3条裤子的搭配，一共有多少种不同的搭配方式？运用“加法原理”可以这样理解，第1类，第1顶帽子搭配3条裤子，有3种不同的方法；第2类，第2顶帽子搭配3条裤子，有3种不同的方法。这两类可以用算式3+3=6表达。运用“乘法原理”理解，则强调分步讨论，第1步，选择2顶帽子中的其中1顶，有2种不同的方法；第2步，选择3条裤子中的其中1条，有3种不同的方法。这两步用算式2×3=6表达。

以下是笔者在本课教学中的一些尝试。

【教学片段】

（一）服装搭配，初步感知计数原理

1.情境导入，自主探究

师：儿童节当天，小丑皮皮接受了到学校表演的邀请，衣柜里有这些服装，皮皮想给自己选一顶帽子和一条裤子，可以怎样搭配呢？

活动1：

请你用学具摆一摆，可以怎样搭配？一共有多少种不同的方法？

2. 有序枚举，初步感知计数原理

学生借助学具摆一摆，有了不同的搭配方法。教师不急于让学生分享汇报，而是引导学生：同学们都摆好了，找到了不同的搭配方法。咱们把这些方法记录下来。

活动2：

記一记：用你喜欢的方式（画一画、记一记或写一写等），将不同的摆法记录下来。

算一算：请用算式表达一共有多少种不同的方法。

3.展示交流，渗透计数原理

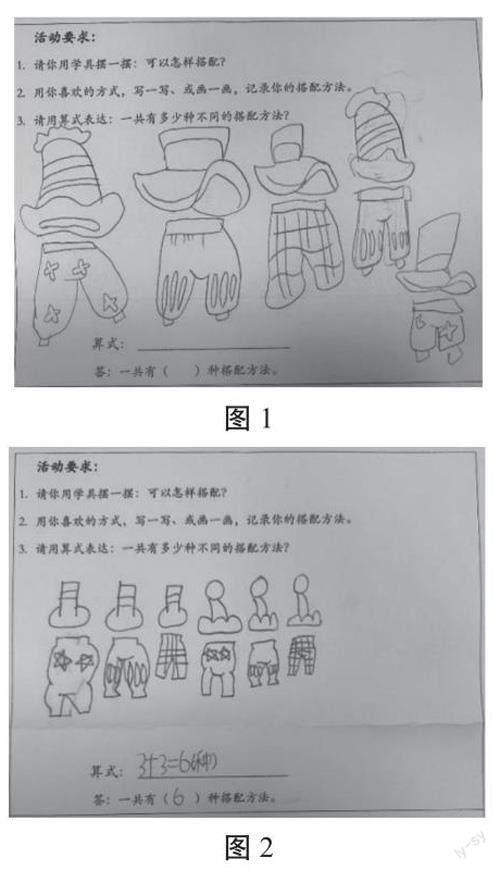
师：对比这两种方法（如图1、图2），哪里不一样？

生1：第一个同学漏了一种方法。

师：那他究竟少了哪一种？

生1：少了尖帽子和格子裤子的搭配。

师：请你分析一下，是什么原因导致他少画了一种？

生1：可能他还没画完。

生2：你看他画得有点乱，如果他能按照顺序画就不会漏了，先用尖帽子搭配3条裤子，再用方帽子搭配3条裤子，3+3=6（种），一共有6种方法，这样就不会有错了。

师：那第二个同学的呢？

生3：他用第1顶帽子搭配3条裤子，第2顶帽子搭配3条裤子。

师：同学们分析得真好啊！也就是说，我们在思考问题的时候，要按照一定的顺序，才能做到不遗漏，也不重复。

思考：在教学中渗透计数原理的思想方法，首先要引导学生有序思考，不遗漏、不重复地找全所有不同的方法。在教学过程中，让学生经历乱序排列及有序排列的对比，感知“有序思考”有助于快速、全面地解决问题。

师：这个同学记录的方式（如图3）跟刚才两个同学的有什么不同？

生1：他们的搭配方法是一样的，只不过这个同学用的是连线，第1顶帽子连3条裤子，第2顶帽子连3条裤子。

师：我们看他的算式是2×3=6（种），这里的2和3分别表示什么？

生2：2表示的是2顶帽子，3表示3条裤子，搭配起来就是6种方法。

思考：相对于逐一画出每种搭配方法，这种连线的方法显然更方便。在搭配过程中，学生已经初步具有分类的意识，懂得运用“加法原理”进行解析。

师：再来看这种记录方式（如图4），你们能看明白吗？

生1：他用三角形表示帽子，用正方形表示裤子。

师：同学们用画图、文字、数字、图形等方式记录了搭配方法。大家认为哪种记录方式更简便？

生2：用图形。

师：是的，我们在记录的时候可以用图形替代。

思考：相对于象形图，抽象图形等记录方式本质是符号记录方式，不同记录方式的逐一呈现，使学生经历具象到抽象的数学化过程，激活学生的符号意识。而符号意识的培养，有助于学生应用计数原理分析问题，因此也是本课的教学重点。

师：再来看这个同学的搭配方法（如图5），与刚才展示的有什么不同？请小组讨论30秒。

生1：他用1条裤子搭配2顶帽子，再用1条裤子搭配2顶帽子，再用1条裤子搭配2顶帽子。一共有6种方法。

师：他没有写算式，你们认为他会用什么算式表达？

生2：2+2+2=6。

生3：2×3=6。

师：刚刚我们也运用了算式2×3=6（指板书），它们表示的意思相同吗？

生4：刚才是用帽子分别搭配裤子，现在是用裤子搭配帽子。

师：也就是说，前面的方法是先选择了帽子，再搭配裤子，而后面的方法是先选择了裤子，再搭配帽子。两者都可以用算式2×3表示。

思考：从不同的思考角度诠释2×3所表达的意义，分步思考（第一步选择帽子，第二步选择裤子；也可以第一步选择裤子，第二步选择帽子），渗透乘法原理。

4.增加一条裤子，巧妙渗透乘法原理

师：当皮皮拿出帽子和裤子时，他发现衣柜里还有一条裤子，现在又有多少种不同的方法呢？

生1：刚刚说1条裤子可以搭配2顶帽子，也就是说在原来的6上面再上2种方法，所以是6+2=8。

师：非常棒！你懂得用递推的方式，在原来的基础上增加两种方法。

生2：还可以用2×4=8。2是2顶帽子，4是4条裤子，1条裤子可以搭配2顶帽子，4条裤子就有8种搭配方法。

师：说得真好，4条裤子，搭配2顶帽子，就可以用2×4=8来表示。

思考：没有操作学具或画图，学生给出算式6+2=8，在原有讨论的基础上递推，理解在原有的3个2的基础上，再增加一个2，也就有了4个2。这说明学生已经能自觉地运用计数原理在脑海里进行图像表征，并用语言描述。

二、路线搭配，体验计数原理的应用

1.变换情境，应用计数原理

师：皮皮在学校表演完了，下午他要赶往动物园参加下一场表演。这是学校到动物园的路线图（图略）。从学校经过少年宫，再到动物园，一共有多少条不同的路线？请你用喜欢的方式记录所有的路线。

师：对比一下，你们有什么想说的？

生1：我认为图6的方法比较好，他把路线图画出来了，我们就知道路是怎么走的。

生2：我认为图7的方法比较好，题目问我们一共有多少条路可以走，而且图6已经标明字母了，走A路再走C路或者D路或者E路，还可以走B路，再走C路或者D路或者E路，一共有6条路线。

师：算式2×3=6表示什么意思？

生3：从A路走，可以选择3条路，从B路走可以选择3条路，所以用2×3=6。

思考：低年级的学生处于具象思维阶段，看到地图抽象出简单的曲线图，是抽象思维的初步发展，而图7学生直接用字母表示，具有一定的符号意识，进一步发展了抽象思维。图7的记录方式及算式表明学生懂得运用加法原理解决问题。

2.各增加一条路

师：如果从学校到少年宫增加一条路，从少年宫到动物园也增加一条路，请思考，从学校到动物园一共有多少条不同的路线？（如图8）同桌之间商量。

生：A和C、A和D、A和E、A和G，這里就有4条路， B也可以和C、D、E、G一起，有4条路，F也是一样的，所以3×4=12。

生：刚才从学校到少年宫有2条路，从少年宫到动物园有3条路，我们用2×3=6表示。所以，从学校到少年宫有3条路，从少年宫到学校有4条路，就用3×4=12表示。

师：是不是这样理解，从学校到少年宫有3条路，我们任选一条，有3种方法，从少年宫到动物园有4条路，任选一条，有4种方法，一共有3×4=12（条）。

思考：学习至此，学生用枚举的策略、迁移的策略，说明乘法原理在起作用。课堂上不明示“计数原理”“加法原理”“乘法原理”等概念，但不影响相关的知识已经渗透。

三、总结提升，联结计数原理

师：请同学们思考“搭配服装”和“去动物园的路线”这两个不同的情境，它们有哪些方面是相同的？

生1：都是搭配问题。

生2：记录搭配的方法是相同的。

生3：比如说，2顶帽子搭配3条裤子，可以用2×3=6，2条路搭配3条路也可以用2×3=6。

师：虽然情境不同，但都属于搭配问题，可以用相同的方法记录，都是可以先选择帽子，再搭配裤子；或者，先选择左边的路，再选择右边的路。这就是我们今天学习的有关搭配的知识。

思考：低年级学生缺乏概括、联结知识的能力，不同情境的对比与归纳，有助于学生总结、概括同类知识，让计数原理的渗透再次得到加强。

计数方法中涉及的“加法原理”和“乘法原理”是高中排列组合的基础，在教材中要到高中才开始学，但这丝毫不影响在小学进行这种思想的渗透。在本节课中，学生通过动手用实物摆一摆、记一记（用自己的方法记录摆的过程）、说一说（将自己记录的方法与同学交流）的活动，对“加法原理”和“乘法原理”有了初步的感悟。