可展开固体反射面天线折展机构设计及分析
2023-12-19马小飞火统龙李欢笑
李 昊, 马小飞, 火统龙, 李欢笑, 吴 迪
(1. 西安空间无线电技术研究所,陕西 西安 710100;2. 西安电子科技大学 机电工程学院,陕西 西安 710071)
1 引 言
随着人类对宇宙空间奥秘的深入探索,传统的卫星已经不能满足人们对外太空信息的渴望,对超大型、高精度的卫星、空间站的发展越发迫切和需要[1-3]。而星载天线作为接收信号的载体,在无线通信、深空探测、卫星遥感和射电天文等领域起着至关重要的作用[4-6]。
受限于运载工具的空间限制,大口径空间天线通常设计为可展开结构[7-9],即在运输过程中呈现收拢态,在到达预定工作轨道后呈现展开态。相比于采用金属丝网[10-12]或薄膜作为反射面[13-15]的传统天线,固体反射面天线由于具有更高的型面精度,可以提供更高的工作频段及增益[16-20]。因此,随着深空探测等天线应用需求的不断提高,固体反射面天线越来越受到研究人员的重视。
典型的固面可展天线通常由一个中心面板与若干旁瓣组成,旁瓣与中心面板共同形成固面天线反射镜面。最早的固面可展开天线是TRW 公司研制的Sunflower[21],该天线由铰接在中心面板上的六块主面板以及相邻主面板之间的6 个子面板组成。然而,这一形式的固面天线收拢后体积较大,且零件数目较多,因此应用并不广泛。当前,应用最多的是欧空局(European Space Agency,ESA)提出的“花瓣式”固面天线[22],其展开过程通常是由2 部分组成,即旁瓣首先绕径向轴线实现径向展开,进而绕旁瓣轴线进行周向翻转完成展开过程。Chae[23]设计了一种以碳纤维增强塑料为反射面的固面可展开天线,采用30 个旁瓣的设计布局,每个旁瓣可独立完成径向展开及周向翻转过程。为提高展开同步性,Bujakas[24]通过设计了一种相似的沿双轴展开固面天线,所不同的是在各旁瓣之间设置了微型线性驱动器用以提高各旁瓣的展开同步性。西北工业大学黄河[25]提出了一种使用扭簧驱动旁瓣沿双轴旋转展开的固面可展开天线,通过仿真分析获得旁瓣展开所需的扭簧预变形,从而满足展开时的型面精度要求。这种布置形式的优点在于可以独立的调节各旁瓣姿态,但同时也因为运动副及驱动源较多,容易造成同步性及可靠性降低。
为解决旁瓣沿双轴旋转展开造成的上述问题,浙江大学徐彦[26]与西北工业大学黄河[27]提出了沿单轴旋转展开的设计方案。该方案以沿双轴旋转展开姿态为基础,通过等效轴角法获得单轴折展运动方案。这一方法需要先以双轴旋转展开姿态为基础,因而无法达到空间中任意姿态,限制了收拢态天线的位形设计。西安电子科技大学谭国栋[28-29]提出了单自由度折展设计方案,并讨论了Bennett 机构在固面可展开天线中的可行性。在此基础上,马军[30]进一步衍生出了RSUR 机构用以控制天线折展。然而上述方法对收拢态与折叠态的旁瓣位形姿态有一定的数值要求,当收拢态位形选择不当时容易使算法无解,同时针对折展机构的过约束问题并没有给出普适性的数学模型作为解决方案。
针对上述问题,本文进行固面可展开天线单自由度折展设计及分析。通过将等效轴角法与粒子群优化算法结合,通过循环迭代求解得出了适用于求解旁瓣绕单轴旋转折展的一般性方法;在Bennett 机构的基础上,进一步进行运动学及动力学分析,并结合变密度拓扑优化方法设计了反射器背架,讨论了背架设计对天线热变形及模态频率的影响;以一款10 m 口径的固面可展开天线为例,进行了详细设计及仿真分析;通过构建并分析折展机构螺旋系,提出了多种避免机构过约束的设计方案,并最终选择RSPRR 机构进行天线非过约束设计,避免了折展机构因严格几何约束可能产生的无法展开问题。
2 可展开固体反射面折展机构设计
2.1 旁瓣展开轴设计
固体反射面天线旁瓣在折展过程中可以视为刚体,因此可以使用空间中不在同一平面的任意三点定义旁瓣在空间中的位置。对于如图1 所示的固面天线折展过程,可以采用A,C,D定义展开状态的旁瓣位置,用A',C',D'定义收拢状态的旁瓣位置。
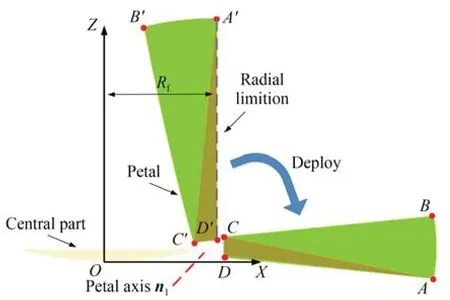
图1 固面天线折展示意图Fig.1 Schematic diagram of deployment of SSDA
根据空间刚体坐标变换原理,旁瓣的展开轴的计算问题可以归纳为三个未知参数的求解:(1)转轴向量nr;(2)旋转锚点P坐标;(3)旋转角度θ。
根据任务需求及天线型面划分,天线处于展开态时旁瓣关键节点的空间坐标通常是已知的,即A,C,D三点坐标已知。由于运载器对天线收拢体积有要求,因此通常可以设置收纳后天线旁瓣的位置,即给定A',C',D'三点坐标。首先需要明确是否存在唯一转轴可以使旁瓣由A',C',D'定义的收拢态位置通过旋转展成至A,C,D三点定义的展开态位置。
以一款10 m 口径固面可展开天线为例,天线的展开外径Da=10 000 mm,中心面板直径Di=3 000 mm,焦距f=4 350 mm,旁瓣数量为24,运载器径向收纳限制Rf=2 000 mm。据此,可以得到A,C,D三点坐标为:
为避免收拢时旁瓣之间的干涉及旁瓣与中心面板的干涉,同时方便收拢态的绑扎,对于收拢态的旁瓣空间位置提出要求为:(1)在XOY平面内观测时,A',C',D'三点都处在与X轴夹角为π/24 的连线上;(2)旁瓣最低点高于中心面板外缘h;(3)从XOZ平面内观测时,A',D'两点连线与Z 轴平行。相比于文献[28]中的计算结果,本文所作约束条件可以使旁瓣外缘与包络圆柱母线重合,更便于收纳。
据此可以假设收拢态时旁瓣的空间位置为:
其中:Rf为收拢外径;Rc'为C'点外径,ZA'为A'点Z向坐标,ZD'为D'点Z向坐标,h为旁瓣最低点与中心面板的距离,C(z)为C点Z向坐标,即中心面板外缘高度;
可以看出,当给定h值时,式(2)的未知数仅为Rc',ZA',ZD'三项。考虑到旁瓣折展过程中为刚体,因此各节点间的距离保持不变,即:
将式(1)和式(2)代入式(3),得到收拢后旁瓣的空间位置:A'(1 982.88,261.05,3 965.54),C'(1 597.57,210.32,181.43),D'(1 982.88,261.05,229.31)。考虑到旁瓣为绕空间某一轴线旋转展开,因此折展前后,转轴向量应始终垂直于AA'和CC'构成的平面、AA'和DD'构成的平面、CC'和DD'构成的平面,据此可以得到:
由于n1,n2,n3不共线,说明在给定坐标下,并不存在可以使旁瓣由指定的收拢态通过一次旋转形成展开态的转轴。
为实现单轴旋转的折展要求,本文提出将指定的收拢态旁瓣位置在限定空间内做出图2 所示的移动,使其达到可以通过一次旋转展开的位形,即:
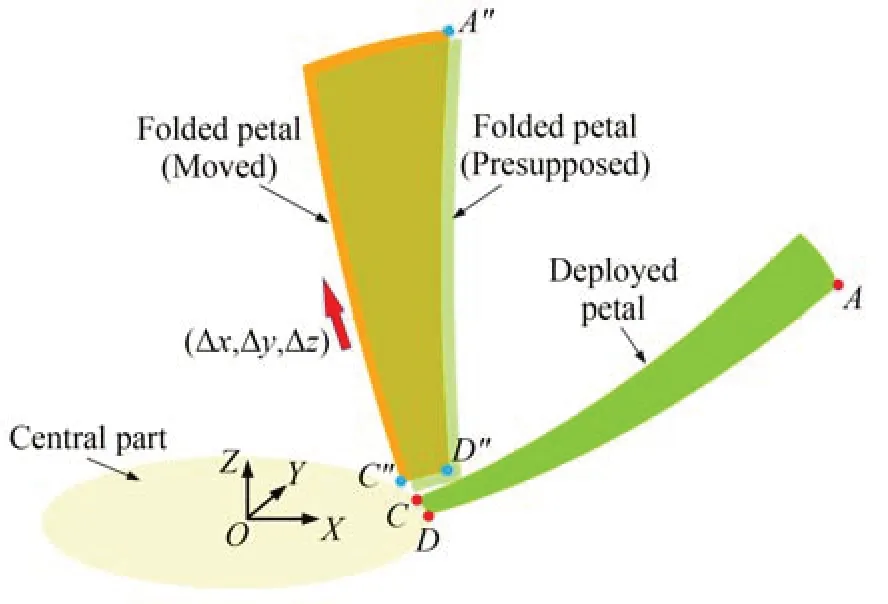
图2 移动旁瓣位置示意图Fig.2 Schematic diagram of petal movement
采用新获取的A″,C″,D″三点坐标更新式(4)所描述的转轴向量:
由于旁瓣绕单轴折展,因此向量n1,n2,n3应为共线的,即:
据此,旁瓣的移动问题就简化为了一个多参数寻优问题,即:通过调整式(5)中的Δx,Δy,Δz,使新获取的A″,C″,D″三点满足式(7)。为解决这一问题,本文采用粒子群优化算法进行多参数优化,构建目标函数G如式所示:
根据式(8)可以看出,此时旁瓣移动问题被抽象为了一个多参数极小值优化问题。当目标函数G足够小时,即可认为新获取的旁瓣位置满足单轴旋转折展的要求。为保证移动旁瓣的过程不会对天线的收纳造成显著影响且不会与中心面板产生干涉,将位移限制在指定范围内,即:Δx∈[-300,300];Δy∈[-300,300];Δz∈[0,300]。
在粒子群算法中[31],一个粒子可以根据其有限的智力和群体的智力来决定自身行动的方向和速度,具体表现为粒子的速度向量v和位移向量s。在实际程序编译过程中,每个粒子的每次行动均代表优化问题的一个解决方案。
在优化过程中,粒子i的第k+1 次行动定义为si(k+1),这一数值在继承上一次行动参数si(k)的基础上,同时引入三个修正向量:
(1)粒子参数的改变量si(k)-si(k+1);
(2)粒子位置与种群最优位置的距离pBestsi(k);
(3)粒子位置与全局最优位置的距离gBestsi(k)。
11月份的皮山农场,虽然寒冷,但与乌鲁木齐的气温来比,还是温暖得多。11月19日,按照兵团“民族团结一家亲”活动工作要求,兵团工会结亲干部一行12人在兵团工会主席黄斌的带领下来到了皮山农场三连,开始为期一周的结亲活动。到达三连,已是下午六点来钟,天已经蒙蒙黑。大家就各自拿上自己的行李,带上为“亲戚”准备的礼物,按照活动方案所分小组奔赴各自的“亲戚”家……
具体数学表达式为:
其中:k为迭代次数;w为惯性系数,用来平衡个体智慧和群体智慧的比例关系;c1,c2为定义的加速系数,反应种群间的信息交流;r1,r2为随机数,提高进化中的随机性;pBest为种群最优解;gBest为全局最优解。
在搜索过程中需要对惯性系数w进行动态调整,目的是权衡全局搜索和局部搜索的关系,以实现在出发阶段的快速探测,在后期进行精细搜索。本节采用的惯性系数调整方法是线性递减权值策略,其表达式为:
其中:wmax为最大惯性系数;wmin为最小惯性系数;k为迭代次数;N为最大迭代次数。
依据优化结果并进行适度圆整后,得到:Δx=-120 mm,Δy=200 mm,Δz=92 mm。即:
移动后的旁瓣径向收纳半径为1 919.05 mm,满足2 000 mm 的收纳要求;C″点高于中心面板边缘129.31 mm,满足旁瓣与中心面板不干涉的要求;A″与D″两点具有相同的收拢半径,满足便于捆扎的要求。
至此,固面可展开天线绕单轴折展的过程简化为求解[A,C,D]T到[A″,C″,D″]T的空间变换问题。根据等效轴角定理,这一过程可以描述为:
其中:Rω(θ)为空间中绕固定轴线旋转θ角的旋转矩阵;CP为旋转轴线矩阵所通过锚点的坐标;I为单位矩阵。
至此,获得了固面可展开天线单自由度展开的运动方案,为后续设计及分析奠定了基础。
2.2 反射器背架设计
对于大口径固面天线而言,为确保展开后的型面精度满足要求,通常需要为旁瓣设置背架使其具有足够的刚度以抵抗变形。图3 为固面天线两个相邻旁瓣展开过程示意图。从图中可以看出,相邻旁瓣的相对位置会在天线展开过程中不断变化,因此仅以收拢态或展开态为依据设计背架就很可能造成运动过程中背架干涉,进而造成天线失效。

图3 相邻旁瓣展开过程示意图Fig.3 Diagram of adjacent petals during deployment
为使折展过程中背架不发生干涉,首先需要获取背架设计空间。图4 为背架设计空间获取过程,建立固连于旁瓣1 的浮动坐标系,分析折展过程中相邻的旁瓣2 在该浮动坐标系下的位姿[28]。当折展过程的时间步长取值足够小时,旁瓣2 相对于旁瓣1 的运动轨迹就可以形成一个包络面,背架设计时只需要避开该包络面即可避免干涉。
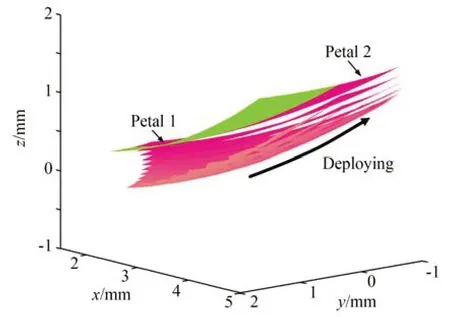
图4 旁瓣背架设计空间Fig.4 Design space of petal frame
在获取得到的背架设计空间内以热变形为约束条件建立背架结构变密度拓扑优化模型,其中旁瓣由碳纤维蒙皮及铝蜂窝芯材构成,材料参数如表1 所示。

表1 天线主要材料参数Tab.1 Material parameters of SSDA
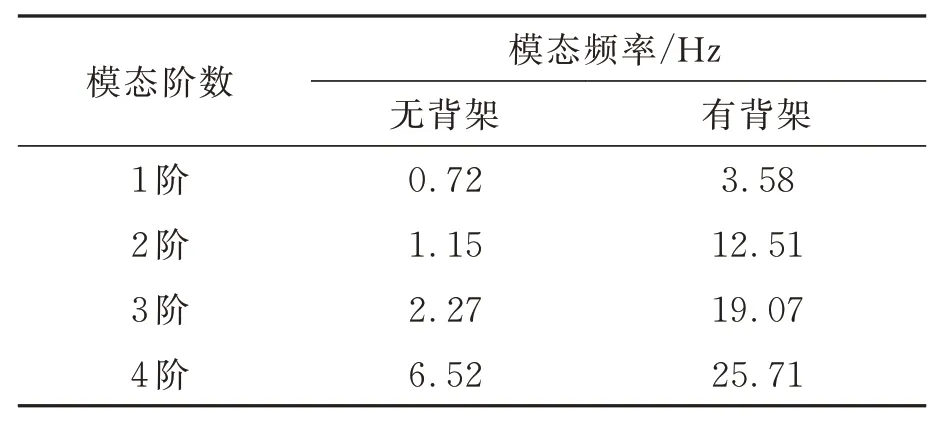
表2 天线模态频率Tab.2 Antenna modal frequency
图5 为拓扑优化结果及背架设计方案。从图中可以看出,高密度区域集中在反射器正面两边缘及背面中线处。据此,设计出了图中“鱼骨状”支撑背架。

图5 旁瓣背架设计空间Fig.5 Topology optimization of petal frame
为验证背架设计的效果,图6 及图7 分别计算了空间环境下(110 ℃)反射器热变形。计算结果显示,采用本节所设计背架可以使反射器热变形最大值由1.92 mm 降低至0.72 mm,降幅为62.5%,佐证了背架设计效果。
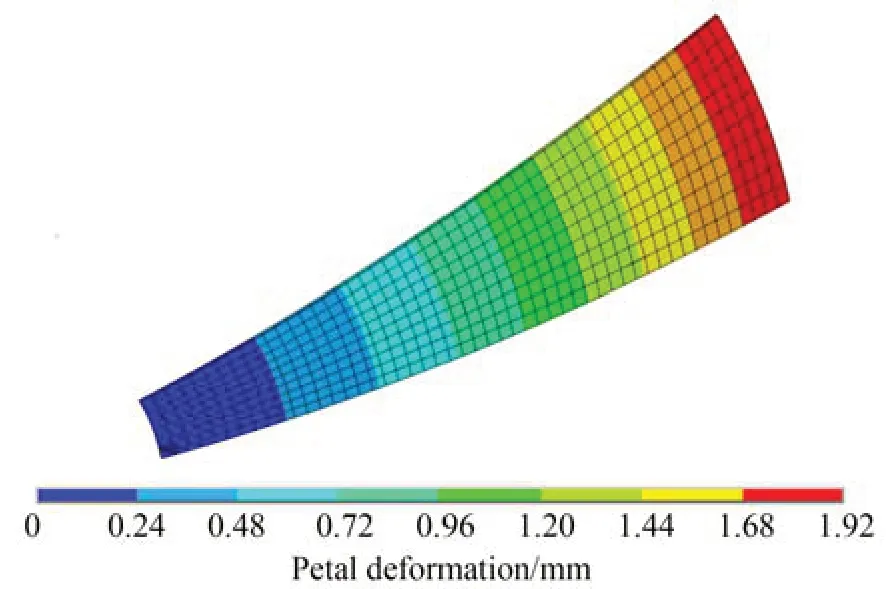
图6 无背架旁瓣热变形Fig.6 Thermal deformation of petal frame without petal frame
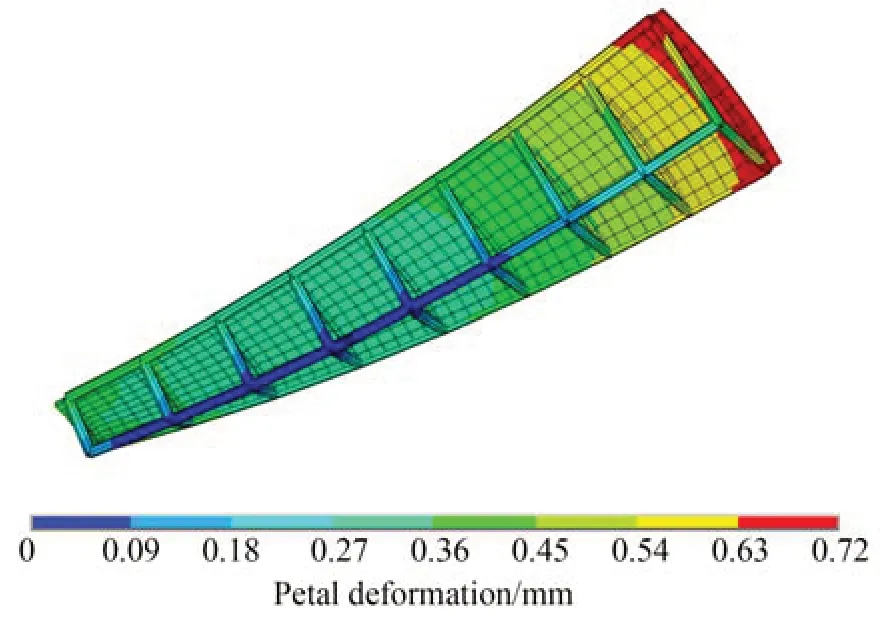
图7 有背架旁瓣热变形Fig.7 Thermal deformation of petal frame with petal frame
图8 为反射器模态分析结果。反射器1 阶及3 阶模态振型呈现沿径向的翘曲,2 阶及4阶振型呈现沿周向的扭转,表3 为反射器面板模态频率计算结果,由于背架提高了反射器整体刚度,因此各阶频率均得到了大幅度的提高。

表3 固面天线折展机构D-H 参数表Tab.3 D-H parameter for deployment mechanism of SSDA

图8 旁瓣模态分析Fig.8 Modal analysis of petal
2.3 折展机构设计
由于收拢态及展开态的固面天线的几何构型均关于抛物面焦点对称,因此将同步转轮的轴线至于通过焦点的中轴线上,形成如图9 所示的拓扑形式[28]。由伺服电机或其他动力源间驱动同步转轮绕转轴nc旋转,同步转轮通过联动机构带动旁瓣绕上一节中计算得到的转轴nr展开。在这一抽象形式中,同步转轮作为输入端,旁瓣作为输出端,则构型综合的核心问题就是解决连接输入端和输出端的联动机构设计方案。
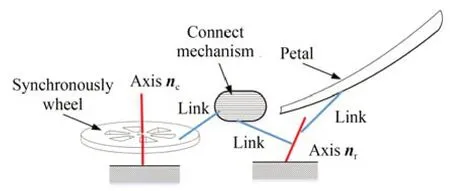
图9 固面天线折展机构拓扑模型Fig.9 Topological model of deployment mechanism
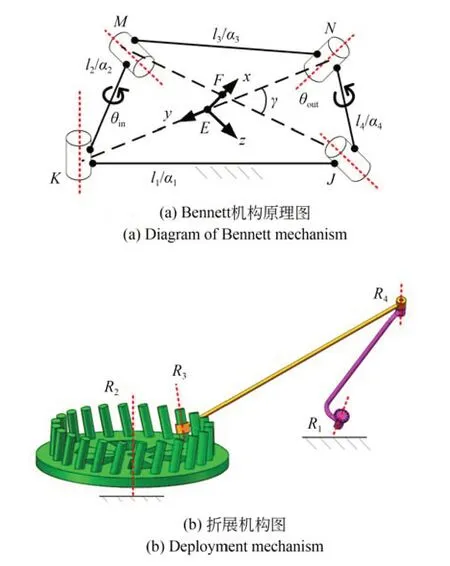
图10 基于Bennett 机构的固面天线折展机构Fig.10 Deployment mechanism based on Bennett linkages
从系统可靠性的角度出发,天线折展机构应尽量采用最少的构件及运动副。同时,从图9 中可以看出,天线的折展过程可以抽象为两空间异面转轴间的旋转运动。因此,本文将沿用Bennett 机构[28]作为旁瓣的折展机构,并进行运动学及动力学分析。
Bennett 机构采用2 组相同的连杆构成,属于空间过约束连杆机构,为满足单自由度的运动要求,需要满足严格的几何约束条件,即:
其中:li为连杆i的长度;αi为连杆i相对于连杆i-1的扭角。
对于本文所述的固面可展开天线结构参数,根据空间向量运算法则,在获得旁瓣转轴向量nr(-0.459 3,0.481 1,-0.746 7)T及同步转轮轴线向量nc(0,0,1)T后,上述Bennett 机构的l1及α1参数已经确定:
其中:NQP为向量n1上一点P与向量n2上一点Q的连线所表示的向量。
按照前文计算结果可得l1=1 216.37 mm,α1=0.727 7。根据约束条件,仅需给定参数l2或α2中的任一参数即可获得完整的Bennett 机构设计方案,由于连杆的长度l2更易通过精密加工及测量获得,因此通常采用给定l2的方法(本文给定l2=400 mm)。
据此,完成了固面可展开天线的折展机构设计,折展过程如图11 所示。
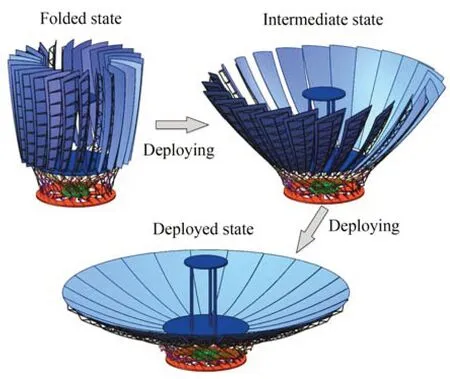
图11 固面天线整体展开过程示意图Fig.11 Deployment process of SSDA
3 可展开固体反射面机构仿真分析
3.1 运动学分析
为描述固面天线的折展过程,在各运动副中心建立D-H 前置坐标系,其中转动副中心轴线为Z轴,其正方向为旋转方向;相邻连杆中心轴线公法线为X轴,其正方向由i-1 杆指向i杆,则各连杆的运动学参数如表3 所示。
表3 中θi为各连杆转角,αi为连杆间转角,li为连杆长度,di为连杆间距。根据D-H坐标系分析原则,可以得出各连杆间坐标系的变换矩阵分别为:
由于Bennett 机构为空间单闭链形式,因此从顺时针及逆时针两个方向开始变换,连杆3 的坐标系在连杆1 坐标系及连杆4 坐标系中的表达式应一致,即:
为方便表述,将连杆1 定为机架,即θ1=0;将连杆2 定为输入连杆,即θ2=θin;将连杆4 定为输出连杆,即θ4=θout。将式(15)~式(18)带入式(19)即可得出:
为使连杆机构平滑运动,使用典型无冲击函数作为输入角参数:
其中:θf为输入角变化总幅值;tf为运动总时长;t为运动时间。
机构运动速度和加速度的变化情况最能反映出天线折展过程中受到冲击的剧烈程度。通过对式(22)及式(23)中的输出转角与输入转角函数分别求导,即可获得旁瓣折展过程中的角速度和角加速度:
依据方程(22)~方程(25)可以计算得到固面天线展开过程中的角度、角速度、角加速度如图12 所示。图中曲线光滑平稳说明了折展过程中无明显冲击及振动发生。同时,输出参数曲线与输入参数曲线近似,这也便于依据输入参数预测折展过程中旁瓣的运动情况。

图12 天线展开过程运动学性能Fig.12 Kinematics parameters of antenna during deployment
3.2 动力学分析
为确保天线能够顺利展开,还需要对展开过程中的驱动力进行求解分析。采用与运动学分析中相同的D-H 前置坐标系,连杆i处质心相对于基坐标系的速度可以表示为:
其中:T0i为连杆i坐标系相对于基坐标系的变换矩阵,ri为连杆i质心位置矢径,θj为连杆j回转角。
连杆i的动能可以表示为:
其中,tr 表示矩阵的迹。
连杆i在基坐标系下的势能可以表示为:
其中,g0为分析工况下的重力加速度,考虑到卸载精度,取分析工况下的重力加速度g0为10-2g。
据此可以获得天线展开过程中的拉格朗日函数为:
由于定义了连杆2 为输入杆,因此对拉格朗日函数L求关于θ2的导数就可以得到展开过程中的广义驱动力。
图13 为不同l2尺寸下,天线展开过程中的驱动力变化情况。驱动力会随着连杆长度的增大而增大,这主要是由于连杆长度增加导致杆组整体质量及惯量增大造成的。对于本文选用的l2=400 mm工况而言,电机驱动力最大值约为17.6 N·m。
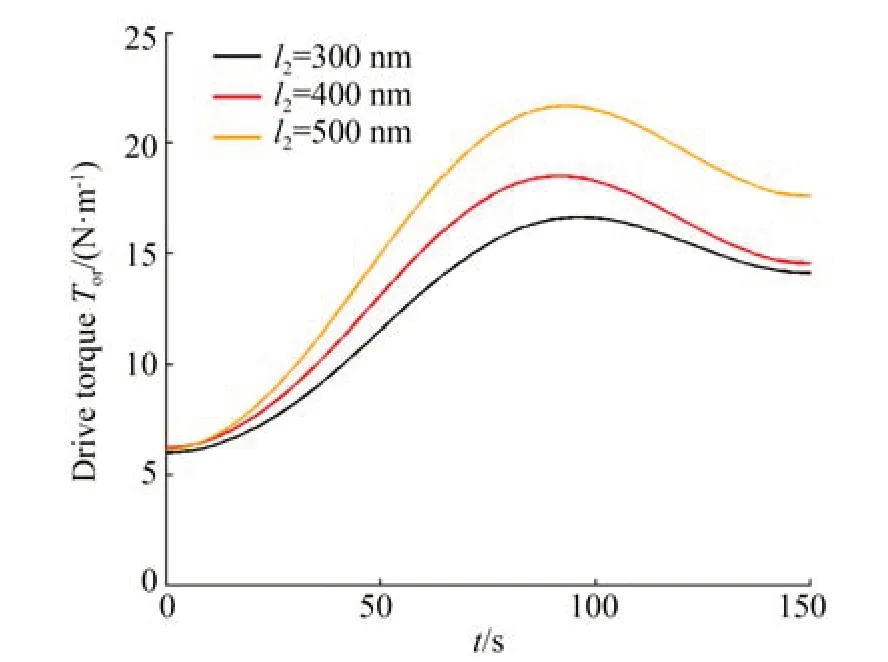
图13 天线展开驱动力Fig.13 Driving moment of SSDA
4 折展机构非过约束设计
由于本文所述的Bennett 折展机构属于过约束机构,只有在满足严格的几何约束的条件下才具有单自由度折展功能。因此为避免因制造及装配误差导致的折展机构失效,需要首先通过引入消极运动副将Bennett 折展机构变为非过约束机构,以使其能够适应制造及装配误差。文献[30]已经注意到了这一问题,并提出了RSUR 机构的替代性方案。本节将通过理论分析,讨论非过约束设计解决方案。
对于图10 所示的折展机构,假设R1及其对应连杆为支链1,R2~R4及其对应连杆为支链2,则构成了一个双支链的并联机构。转动副R1~R4所对应的运动螺旋为$1~$4。设对角线KN=2l,JM=2m,且对角线夹角为γ。KN与JM的中点分别为E,F,且EF=n。取E点为原点,EF方向为X轴,EK方向为Y轴,建立图10中所示的坐标系。4:J(n,-mcosγ,msinγ),K(0,l,0),M(n,mcosγ,-msinγ),N(0,-l,0)。
支链1 的运动螺旋$1可以表示为:
运动螺旋$1对应的约束螺旋为:
支链2 的运动螺旋为:
由于JK为机架,KM和JN分别为输入杆和输出杆,为保证运动规律不发生变化,可以在M或N处引入消极运动副,本文选择在N处引入消极运动副。依据并联机构消极运动副引入规则,消极运动副对应的螺旋系N3应属于N1但不属于N2。考虑到Bennett 机构的阶数为3,为使机构变为非过约束机构,需要引入的消极运动副所对应螺旋系的秩应为3。因此,在N处引入消极运动副的组合可以为RRR,RRP,RPP 及PPP 四种,由于N处已有转动副R4,为满足N3不属于N2,RRR 副的组合形式不成立。考虑到R副的运动精度通常高于P副,因此本文在N处引入RRP 形式的消极运动副,结合N处原有转动副R4,可将N处运动副进一步简化为图14 所示的PS 组合。此时,可以得出消极运动副的螺旋系N3为:
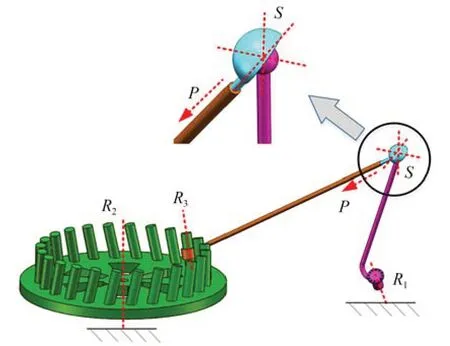
图14 折展机构非过约束形式Fig.14 Non-overconstrained form of deployment mechanism
将公式(33)展开并带入相关数值可以证明此时的N3秩为3,且满足(N3∈N1,N3∉N2)。因此,图10 所示的过约束机构已经转化为RSPRR非过约束机构,当存在制造或装配误差时,机构仍可以实现单自由度折展效果。
事实上,当将M处与N处同时作为消极运动副的引入位置时,采用上述螺旋理论分析方法则可以构建出RSUR,RUSR,RSSR,RSPRR,RSCR,RCSR,RURPPR,RUCPR,RRPPPRR,RCPCR 等大量非过约束设计形式,可以依据实际设计要求进行选取,此处不再赘述。
5 结 论
本文针对固面可展开天线的展开机构,设计并分析了一种单自由度折展方案,主要结论如下:
(1)为实现单轴旋转展开的任务需求,提出了基于粒子群算法的收拢态旁瓣位形确定算法,结合等效轴角定理给出了单轴旋转展开的参数确定方案;
(2)以相邻旁瓣运动轨迹为基础,结合拓扑优化方法给出了反射器背架设计方案,并进行了热变形及模态分析,分析结果表明本文提出的背架设计方案可以有效降低反射器热变形,同时大幅提高模态频率;
(3)以一款展开口径为10 m 的固面可展开天线为例进行了天线折展机构设计,通过运动学及动力学分析,研究了天线折展过程中角位移、角速度、角加速度及驱动力矩的变化规律;
(4)通过构建折展机构螺旋系提出了多种消极运动副引入方案,并最终采用RSPRR 非过约束机构,避免了折展机构因严格几何约束可能产生的无法展开问题。
