基于数学抽象素养的概念课案例及其思考
2023-12-17王伟
王伟
[摘 要] 以“函数”的教学为例,在数学抽象的基础上进行课堂教学过程的构思,促进教师对概念课教学如何培养学生数学抽象素养的深入思考.
[关键词] 数学的眼光;数学抽象素养;抽象能力;概念教学;函数
《义务教育数学课程标准(2022年版)》提出要培养学生的核心素养(“三会”),其中“会用数学的眼光观察现实世界”的核心就是数学抽象素养. 所谓数学抽象素养,是指通过对数量与数量关系、图形与图形关系两方面抽象出数学概念及概念之间的联系,从事物与事物之间的联系、事物内部之间的联系抽象出一般规律和结构,并用数学语言加以表征的素养. 在现阶段初中数学实际教学中,教师大多重视学生解题,很少关注学生数学抽象素养的培养. 在一次宁波市课堂教学评比活动中,对“函数(1)”(浙教版《数学》八年级上册第5章第2节)这节课,笔者从“数学抽象素养”的角度进行教学,让学生经历层次清晰、完整的抽象过程(从具体的数学情境中抽象出数学概念 →从数学概念与概念之间抽象出数学关系→从数学问题解决过程中抽象出数学思想方法),取得良好的效果. 现将具体设计与思考整理成文,供同仁参考研讨.
教学过程
1. 经历从现实情境中抽象出函数的过程——明确研究对象
情境1 电影《我和我的家乡》为祖国71周年华诞献礼,定于10月1日8点在全国各大电影院上映.
(1)象山时代金球影城,票价35元一张,请问电影院每场的收入相同吗?为什么?
(2)若10月1日12:00场卖出60张票,收入是多少元?
(3)12:45场卖出80张票,收入是多少?
(4)若活动价定于20元/张,请同学们完成下表(见表1).
师追问:
问题1.1计算的过程中,哪些量是常量?哪些量是变量?
问题1.2哪个量随着哪个量的变化而变化?
问题1.3用x表示销售票数,y表示每场收入,可以用关于x的代数式表示y吗?
问题1.4当x的值确定后,y的值确定吗?有几个?
情境2 电影院每场次电影播出需要固定成本171元,国庆期间又推出一张电影票送一枚中国心吊坠活动.
问题2.1电影院每场的成本与哪些量有关?
问题2.2每个中国心吊坠成本6.6元,销售票数x张,每场成本m元,m与x之间的等量关系是什么?
问题2.3你可以输入计算的EXCEL表格程序来解决成本的运算吗?
问题2.4输入几个x的值,观察m的值的变化. 当x的值确定后,m的值确定吗?有几个?
情境3 在等候电影期间,小明了解到工作人员小聪的工资报酬按16元/时计算,设小聪这个月工作的时间为t小时,应得报酬为m元,填写下表(见表3):
问题3.1在这个变化的过程中,有几个变量?分别是什么?
问题3.2哪个量随着哪个量的变化而变化?
问题3.3给定一个t的值,我们可以得到几个对应的m的值?怎样用关于t的代数式表示m?
问题3.4y与x,m与x,m与t的这种关系相同吗?是怎样的关系?
设计意图 以国庆节电影票、中国心吊坠、工作报酬引入,不仅使学生感受到新知与生活的联系,认识到研究新知的必要性,而且激发了学生的学习兴趣和爱国主义情怀. 对于情境中的所有信息,学生通过观察、识别、比较等认知行为提取出与概念相关的关键信息,再进行计算、分析、比较等思考后确定抽象的对象是变量之间的关系,对函数的本质属性有了初步的认识. 函数的本质属性过于抽象,Excel表格的动态功能可以突破课本中x,y的人为预设、静态、单一的缺陷,它像一个函数转化器让学生直观、生动地看到函数概念的内涵.
2. 参与定义函数的活动——形成函数的概念
根据上述分析,进行归纳概括.
问题4.1 抛开实际背景,上述三个情境中的变量和变量关系都有哪些共同特征?
问题4.2 这些特征是否适用于一般的同类的变量关系?
教师在倾听学生观点的基础上进行总结性讲解:它们的共同特征是,每组关系都涉及两个变量;对于一个变量的每一个确定的值,另一个变量都有唯一确定的值与之对应. 这样的变量关系在数学上称为函数.
问题5尝试用文字语言给函数下个定义.
通过对问题5的分析,抽象得到:一般地,在某个变化过程中,设有两个变量x,y,如果对于x的每一个确定的值,y都有唯一确定的值与之对应,那么就说y是x的函数,x叫作自变量. 例如:上述变量关系中,m是x的函数,x是自变量……
设计意图 根据学生的思维特征,在概念教学中,必须遵循从具体到抽象的原则,必须经历对学习材料进行“观察比较—感知辨认—加工提取—建立表象”的概念“再创造”过程. 在明确研究的对象是变量的关系时,学生通过比较、归纳、概括等复杂思考提取共性(变量的规律及变量之间的关系)后建立清晰的函数概念表象,这使学生感受到了更高层次的数学抽象,积累了抽象概括的活动经验. 在用数学语言对函数概念加以表征时,八年级的学生还缺乏相关的经验和能力,此时需教师价值引导.
3. 了解函数的三种表达形式——感悟数形结合思想
解析法:像m=6.6x+171这样表示函数关系的等式叫作函数表达式,简称函数式,用函数表达式表示函数关系的方法也叫作解析法.
女生跑800米,成績与时间成函数关系,见表4:
把自变量的一系列值和函数的对应值列成一个表,这种表示函数关系的方法叫作列表法.
如图1,这种用图象表示函数关系的方法叫图象法.
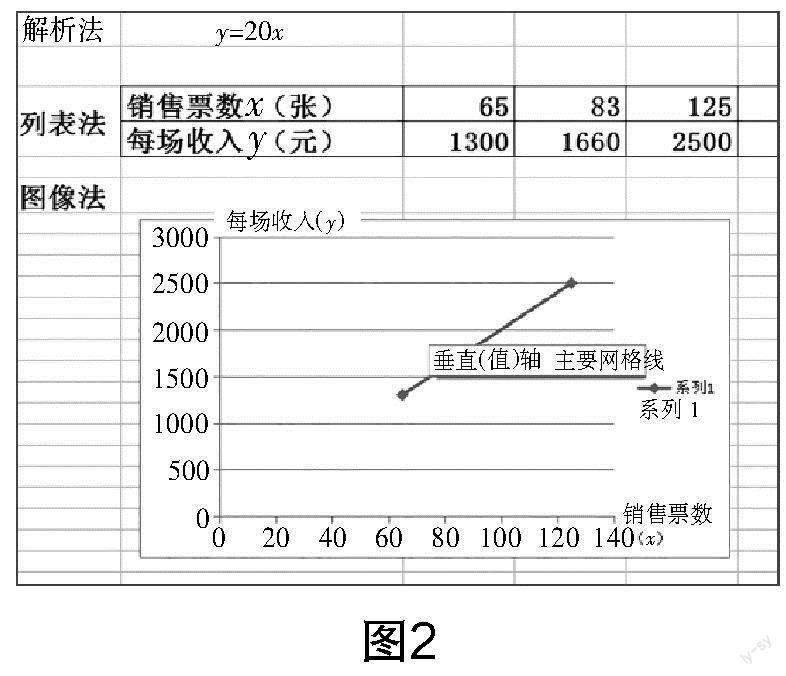
归纳总结:同一个函数问题可以用三种不同的形式来表示(如图2),这三种形式如何转化我们要留着以后探索. 这三种表达形式各有什么优点呢?
设计意图 结合实例了解函数的三种表示方法,即列表法、解析法、图象法. 通过计算、查表、图象找点感受“一个变量确定,另一个变量随之唯一确定”,突出函数的本质属性,剥离“用公式表示变量关系”这一非本质属性. 从函数定义的文字叙述到三种表达形式:符号、表格、图象,从文字到符号,这是数学抽象的重要环节,从符号到图表,这是从抽象到具体,符合学生的认知规律. 举例同一个函数问题可以用三种不同的形式表达,渗透了数形结合思想. 这样的数学活动加深了学生对函数本质的理解,有助于培养学生的发散思维,能让学生体会到数量关系和几何图形的联系,加强了数与形对应关系的意识.
4. 参与知识与技能的应用的活动——解答有代表性问题
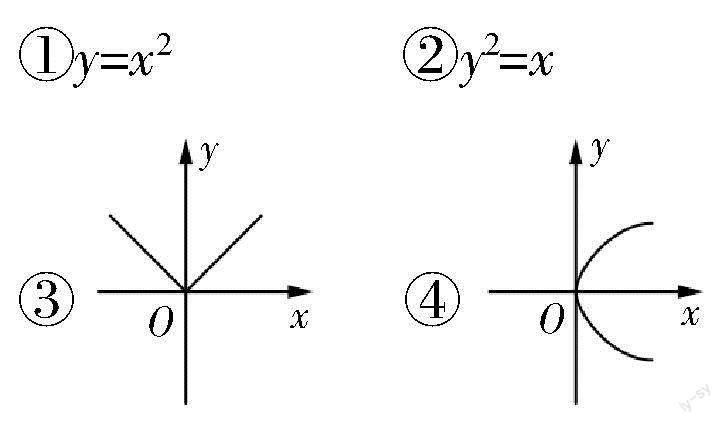
(一)辨一辨
y是关于x的函数的是______.
(二)举例:
请举一个生活中的函数的实例.
(三)实际应用
某汽车油箱有20升油,它在高速公路上行驶,耗油量为0.07升/千米,汽车行驶的里程为x千米,油箱中剩下的汽油量为y升 .
①写出y与x之间的函数解析式;
②求当x=20时的函数值,并说明它的实际意义;
③象山距离上海293千米,可以到达吗?为什么?
设计意图 形成函数的概念后,及时进行函数概念的辨析,通过正例和反例让学生明确概念的外延. 追问为什么,进一步加深学生对函数内涵的理解. 通过学生举例,体会函数是刻画现实世界重要的工具,促进学生对概念外延的进一步把握. 实际问题的解决让学生经历概念的“具体—一般—具体”的过程,形成用数学的眼光(函数的观点)认识现实世界的意识,体会蕴含在应用过程中的函数思想和方法. 在实际问题的解决过程中概括出解题的一般步骤,感悟到模型思想,学生在这一过程中发展了数学抽象素养.
5. 参与回顾与梳理的活动——提炼内化分享
教师出示问题清单,学生围绕问题清单进行思考:
(1)学习了函数的哪些知识?
(2)我们是如何学习函数的,后续还要学习什么?
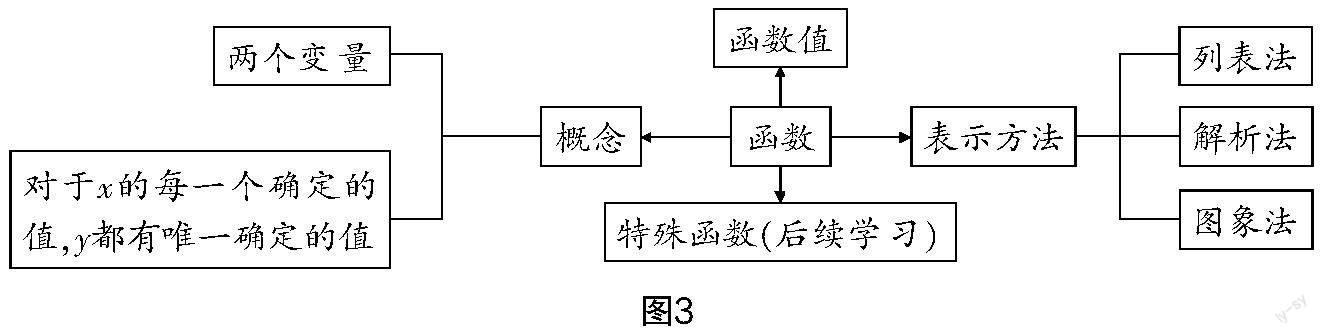
(3)梳理这节课的研究思路,并绘制相应的知识框图.
设计意图 以“问题清单”式的反思性问题引导学生回顾与思考,在此基础上师生共同绘制知识框图(如图3),促进学生函数概念的系统化与结构化,增强了学生的反思意识,发展了学生的语言表达、抽象等多种能力,从而有利于学生理解数学、学好数学. “函数”的研究路径为今后学习类似的问题提供了方向引领和方法指导.
教学反思
1. 培养学生数学抽象素养,教师需创设情境型问题链
史宁中教授认为抽象有两个层次:一是从感性具体到理性具体;二是符号化. 具体来说就是将现实的问题数学化,从数学要素中发现数学关系、概念、命题等. 基于此,教师需创设有效的情境型问题链. 有效的情境型问题链首先情境不仅真实,有内涵,而且包含学生所不熟悉的新知识;其次它能引发学生进行分析、比较、概括等复杂思考. 本文中情境1、情境2、情境3分别是关于电影院里的电影票、电影院每场成本、营业员工作报酬的生活情境,为函数的学习提供真实性的生长点,引出函数学习的必要性. 情境1中追问的问题1.1以旧忆新,提供函数概念的生长点:变量;问题1.2引出研究对象是变量之间的关系;问题1.3将变量之间的关系符号化,隐含函数的单值对应关系;问题1.4进一步探讨变量之间的单值对应关系;问题3.4探讨三组变量关系的共性特征.上述问题链的问题层次清晰、有梯度,为学生抽象概念搭好了“脚手架”,最终达成了数学抽象素养的培养.
2. 培养学生数学抽象素养,学生需经历完整的数学抽象过程
学生的数学抽象素养是在抽象过程中逐步孕育的,并且只有完整的抽象过程才能培养出抽象能力,并最终发展为数学抽象素养. 因此,数学教学应再现抽象的过程,强化抽象的过程. 本文中学生经历了以下四方面的抽象过程:一是从具体的生活情境中抽象出数学问题;二是从变量与变量之间的关系抽象出函数的概念;三是从数学问题的解决过程中抽象出“一般到具体”、函数等数学思想;四是在归纳总结中形成函数概念的系统化与结构化. 学生在层次清晰的抽象过程中参与抽象、尝试抽象,积累了概况抽象的活动经验,数学抽象素养也在抽象经验的积淀与升华中养成.
参考文献:
[1]中华人民共和国教育部. 义务教育数学课程标准(2022年版)[M]. 北京:北京师范大学出版社,2022.
[2]史宁中. 数学基本思想18讲[M].北京:北京師范大学出版社,2016.
[3]李昌官. 数学抽象及其教学[J].数学教育学报,2017,26(04).
