GRACE Level-2数据的RTS状态平滑

凤 勇,常国宾,钱妮佳,魏征强,宦越洋,杨一帆

中国矿业大学环境与测绘学院,江苏 徐州 221116

全球气候变暖导致的冰盖融化、海平面上升是制约人类社会发展的重大问题。GRACE卫星自2002年3月发射到2017年7月结束任务,对全球重力场变化进行了十几年的观测。目前GRACE卫星重力技术广泛应用于陆地水存储量变化、南极和格陵兰岛冰盖质量变化及全球海平面变化等研究[1-2]。后续GRACE-FO(GRACE follow-on)卫星的发射为继续研究地表物质迁移提供基础数据。

球谐系数反演法计算简单,应用较为广泛,但受到卫星载荷的仪器测量误差、混频误差、卫星轨道、先验模型误差和时变重力场截断误差的影响[3-5],不同研究中心发布的GRACE level-2产品解算出来的地表物质迁移反演结果存在显著的南北方向条带。除此之外,GRACE时变重力场模型球谐系数存在明显的高频噪声,尤其是40阶后的重力场位系数,其噪声大于信号,主要原因是GRACE卫星轨道设计缺陷、背景模型误差及星上载荷测量精度导致的观测误差等的共同作用[6-7]。本文利用状态空间模型对GRACE level-2产品处理以削弱条带误差。用到GRACE level-2产品包括截断至60阶的球谐系数以及球谐系数对应的形式误差协方差矩阵。

为削弱误差对真实信号的影响,往往会对数据施加某种约束,这种约束大体上可划分为两类:一是空间约束,利用数据在空间域上存在的联系,对数据加以约束,例如各向同性或各向异性平滑[8]、经验去相关[9]、基于反演或正则化的去相关去噪核(decorrelation and denoising kernel,DDK)滤波[10-12]、独立分量分析(independent component analysis,ICA)[13]等;二是时间约束,对同一组观测量进行连续观测构成时间序列,运用合适的方法表征观测量在时间域上的特性,比如小波分析[14]、时差正则化[15]等。有些方法不仅存在空间约束,还同时兼顾时间约束,比如,主成分分析(principal component analysis,PCA)[16-17]、奇异谱分析(singular spectrum analysis,SSA)[18]等。容易发现,上述时间域约束是一类定性层面的非参数化方法,没有将形式误差协方差矩阵考虑进来,因而损失大量统计信息。参数化的方法也不乏学者研究,比如用关于时间的多项式来参数化重力信号(球谐系数),用关于球谐系数次数的多项式函数来参数化条带误差,所有参数都用加权最小二乘法同时进行估计。本文所研究的状态空间模型法也是一种参数化方法,采用状态空间模型对信号进行参数化表示,进而采用卡尔曼滤波对GRACE Level-2球谐系数进行处理,以达到降噪和去条带的效果。本文方法可以综合利用真实地球物理信号的协方差矩阵及条带误差的协方差矩阵,不仅反映条带误差的空间域特征,而且能反映地球物理信号在时间域上的相关性。

首先,状态向量中仅包含表示真实地球物理信号的球谐系数,GRACE Level-2产品中的测量误差协方差矩阵被用作状态空间模型中观测误差协方差矩阵。然后,状态向量的协方差矩阵用一个仅与阶数有关的幂律模型来表示,以便提供月与月之间球谐系数的不确定性度量;引入一个尺度因子(方差分量)表示该不确定性的总体幅度,并根据数据对该因子进行自适应调整。最后,将平滑解而非滤波解作为最终的结果,进一步改善数据处理效果[19-20]。

DDK滤波代价函数由正则化项和残差加权平方和项两部分组成,分别涉及信号协方差矩阵和误差协方差矩阵,恰与状态空间DDK滤波方法(state space decorrelation and denoising kernel,SS-DDK)中的过程噪声协方差矩阵和观测噪声协方差矩阵相对应,只不过SS-DDK中的过程噪声协方差矩阵表示球谐系数在相邻月份变化的统计信息,而DDK中的信号协方差矩阵表示的是信号在单个月份的统计信息,这一相似性是本文方法名称中“DDK”的来源。

1 数据和方法

1.1 数据

采用美国得克萨斯大学空间研究中心(Center for Space Research,University of Texas at Austin)提供的2002年4月至2014年6月共135个月GRACE Level-2(Release-05)数据。该数据为60阶无约束球谐系数,并扣除了非潮汐大气、高频海洋信号、各种潮汐、固体潮和固体极潮等影响。数据包括球谐系数yk,球谐系数对应的完整形式误差协方差矩阵Rk,下标“k”表示月份。丢失数据的月份直接舍弃,若第二个月数据丢失,可以简单地将下标“2”用来表示第三个月的数据。

1.2 状态空间模型

表示真实地球物理信号的球谐系数xk是待估计的变量,与yk有相同的维数。状态空间模型的观测模型表示为

(1)

式中,观测矩阵Hk是单位阵。观测误差vk一般包含高频误差和条带噪声等。条带噪声的统计规律与时间无关,是一种时间域纯随机误差,即白噪声,将条带噪声纳入vk中加以考虑,而不是将其作为状态向量的一部分,这更符合实际,也可降低状态向量的维数,认为条带噪声的统计信息全部包括在观测噪声协方差矩阵中(事实也是如此),则无须对条带噪声统计信息进行其他人为设置,简化了建模工作量,提高模型可靠性,这是本文状态空间法与前人最大的不同之处。

状态转移方程(过程模型)表示为

(2)

式中,状态转移矩阵Fk是单位阵;Q是过程噪声协方差矩阵,一般为对角阵,考虑到GRACE存在月份缺失问题,Qk=mkQ,mk表示yk与yk-1之间的月数差,Q的对角线元素根据幂律模型得到,幂律模型的幂指数表示为-μ,底数为阶数l;α表示方差分量。式(2)表示对任意阶次的球谐系数采用的均为随机游走过程模型。DDK和SS-DDK滤波解分别为

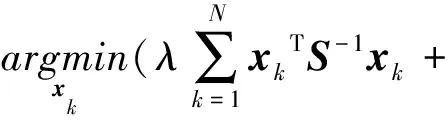
(3)

(4)

不难发现,式(3)和式(4)存在相似之处,均包含观测误差所构成的代价函数这一项。式(3)中引入正则化因子λ和信号协方差矩阵S[12],并根据Roelof Rietbroek发布在Github上关于DDK滤波器的软件(https:∥github.com/strawpants/GRACE-filter),进一步得知从DDK1到DDK8,λ取值介于5×109～1×1014之间,矩阵S的对角线元素为l-v,l表示阶数,指数v一般取4。式(4)引入方差分量因子α和过程噪声协方差矩阵Q,其中α根据公式迭代计算得到,矩阵Q则和矩阵S设计相同,均由幂律模型得到,幂指数μ取4。式(3)和式(4)所体现出的相似性正是将本文方法命名为“SS-DDK”的原因。

1.3 状态估计

给定建模参数,最优状态向量估计一般选用卡尔曼滤波或平滑[21]。这里给出卡尔曼滤波的计算公式

(5)

(6)

(7)

(8)

(9)

RTS(Rauch-Tung-Striebel)平滑是一种最为常用的固定间隔平滑方法,公式为[22]

(10)

(11)

(12)

(13)

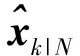
PN,N-1|N=(E-KkHk)Fk-1Pk-1|k-1

(14)

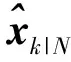
1.4 参数估计

卡尔曼滤波解和RTS平滑解容易得到,然而建模参数α是未知的。本文试图同时找到状态向量和建模参数的最大似然估计。对应的代价函数,即负对数似然函数为

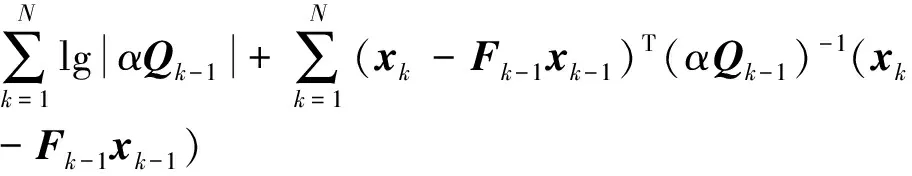
(15)

注意Qk中包含幂指数μ。当使用EM算法进行参数估计时,E-step输出只含建模参数为未知数的近似代价函数[23]

(16)

M-step中找到使得近似代价函数式(16)取得最小值的参数α。经证明,存在如下封闭形式的解

(17)

其中Dk的计算公式如下

(18)

如图1所示,详细阐述SS-DDK实施步骤。步骤1对GRACE Level-2数据进行预处理,根据给定的幂指数和阶数构建过程噪声协方差矩阵Q;步骤2是人为给定初值和初始协方差矩阵,并假定尺度因子(方差分量)α的初值为1;步骤3按式(5)—式(9)逐月计算状态向量的卡尔曼滤波估计值和对应协方差矩阵;步骤4按式(10)—式(14)计算RTS平滑解以及相应协方差矩阵;步骤5运用卡尔曼滤波解和RTS平滑解求得尺度因子α的更新值;步骤6判断参数α是否收敛,若收敛,输出RTS平滑解作为最终处理结果,否则,更新尺度因子α继续执行步骤3—步骤6,直至迭代停止。

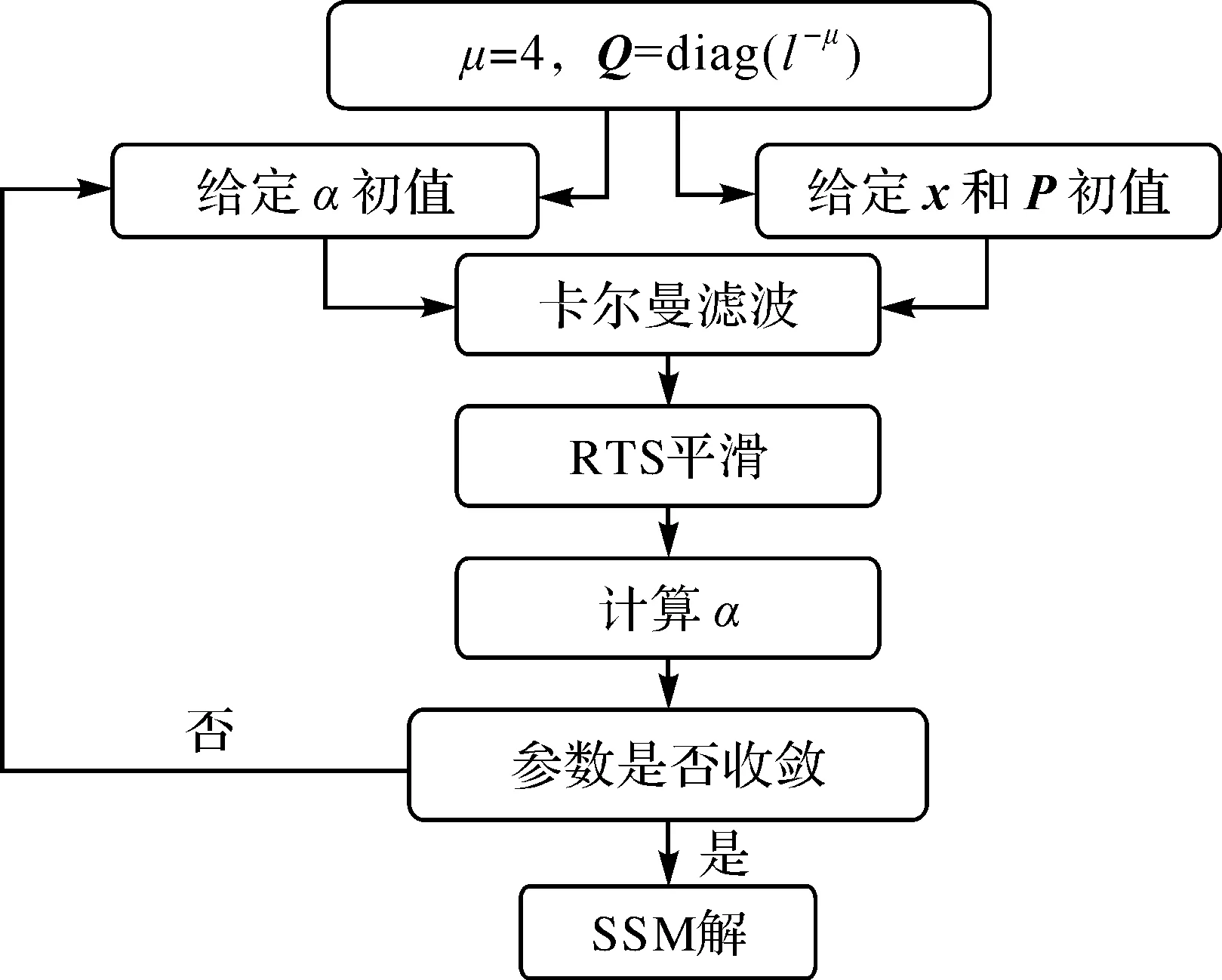
图1 状态空间建模流程

按状态空间流程图(图1)进行迭代处理,得到迭代50次的结果,最后参数α大约收敛至1×10-19(图2)。

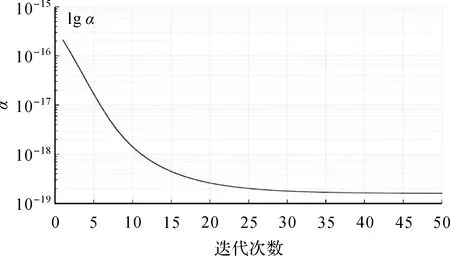
图2 状态空间模型中方差分量因子α随迭代次数的变化

2 试验和结果讨论

2.1 滤波质量异常分析

美国得克萨斯大学空间研究中心目前只发布RL05球谐系数解的协方差矩阵,故没有选用RL06数据进行处理。RL05数据可以从网站(http:∥download.csr.utexas.edu/outgoing/grace/)下载。该网站仅提供2002年4月至2014年6月的数据,后续GRACE在轨运行期间的数据暂未提供。这135个月数据足以验证SS-DDK方法的性能。试验前先做如下预处理:从球谐系数中扣除该时段的平均值;用卫星激光测距(satellite laser ranging,SLR)[24]结果替换球谐系数C20项;地心1阶项由GRACE卫星和海洋模型联合估计得到;利用ICE-6G_D模型进行冰川均衡化调整(glacial isostatic adjustment,GIA)。选用DDK1—8滤波与本文SS-DDK对比。CSR RL06 v2.1 mascon解(https:∥www2.csr.utexas.edu/grace/RL06_mascons.html)可以得到局部较好的质量变化估计[25-26],故将其作为参照数据。

大地水准面是一个重力等位面,大地水准面高可由时变重力场球谐系数计算得到,地球表面及其内部的物质运动引起大地水准面高度的变化(ΔN),公式为

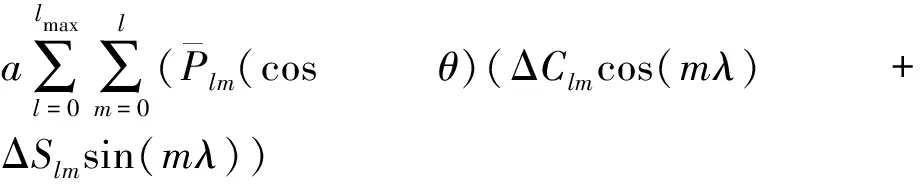
(19)

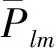
ΔSlmsin(mλ))

(20)

式(20)得到全球范围内等效水柱高变化[27],其中ΔH表示等效水柱高变化;ρave为地球平均密度,取5517 kg/m3;ρω为水的密度,取1000 kg/m3;kl为l阶的负荷勒夫数。在扣除冰川均衡化调整并且没有地震影响的情况下,EWH变化即表征地表质量变化。

本文以2006年1月、3月、6月、12月为例,图3为SS-DDK、DDK3和DDK5滤波解及0.25°×0.25° mascon解的EWH变化,图4为球谐系数无约束解和其余DDK滤波解的EWH变化。从图3和图4中不难发现,DDK1—8滤波的约束能力依次减弱,DDK1的约束能力最强,全球范围内南北条带去除得最干净,但局部区域出现失真现象,尤其是高纬度地区,如格陵兰岛;DDK8的约束能力最弱,局部区域信号保留较好,但是存在明显的条带噪声。一般地,DDK3—5滤波的效果最佳,可以在去除条带噪声的同时保留更多有用的信号。重点关注南美洲亚马孙河流域、非洲刚果河流域、我国长江流域、印度恒河流域和格陵兰岛5大区域的信号保留,以及去条带情况。经SS-DDK滤波之后,能够很好地削弱条带误差的影响,几乎看不到明显的条带存在,并且在上述5大区域,可以较为清晰地看到EWH的变化,例如在亚马孙河流域,2006年6月前后等效水柱高EWH为正值,并且变化异常明显,而在2006年12月前后EWH为负值。再例如格陵兰岛区域,SS-DDK与DDK3—8一样保存了绝大部分的地球物理信号,不像DDK1—2那样具有明显的信号失真。比较SS-DDK和DDK1—8与mascon在格陵兰岛区域的EWH变化发现,任何滤波解都存在不同程度的信号泄漏现象。泄漏误差不是本文的研究重点,故这里不做过多展开。以mascon解为参考,计算2002年4月至2014年6月整个时间段全球720×1440个格网点EWH的均方根差异(root mean square differences,RMSD)见表1,SS-DDK的均方根最小,DDK3的均方根与SS-DDK最为接近,从全球来看,SS-DDK方法要优于DDK系列滤波。

表1 全球格网点EWH的均方根

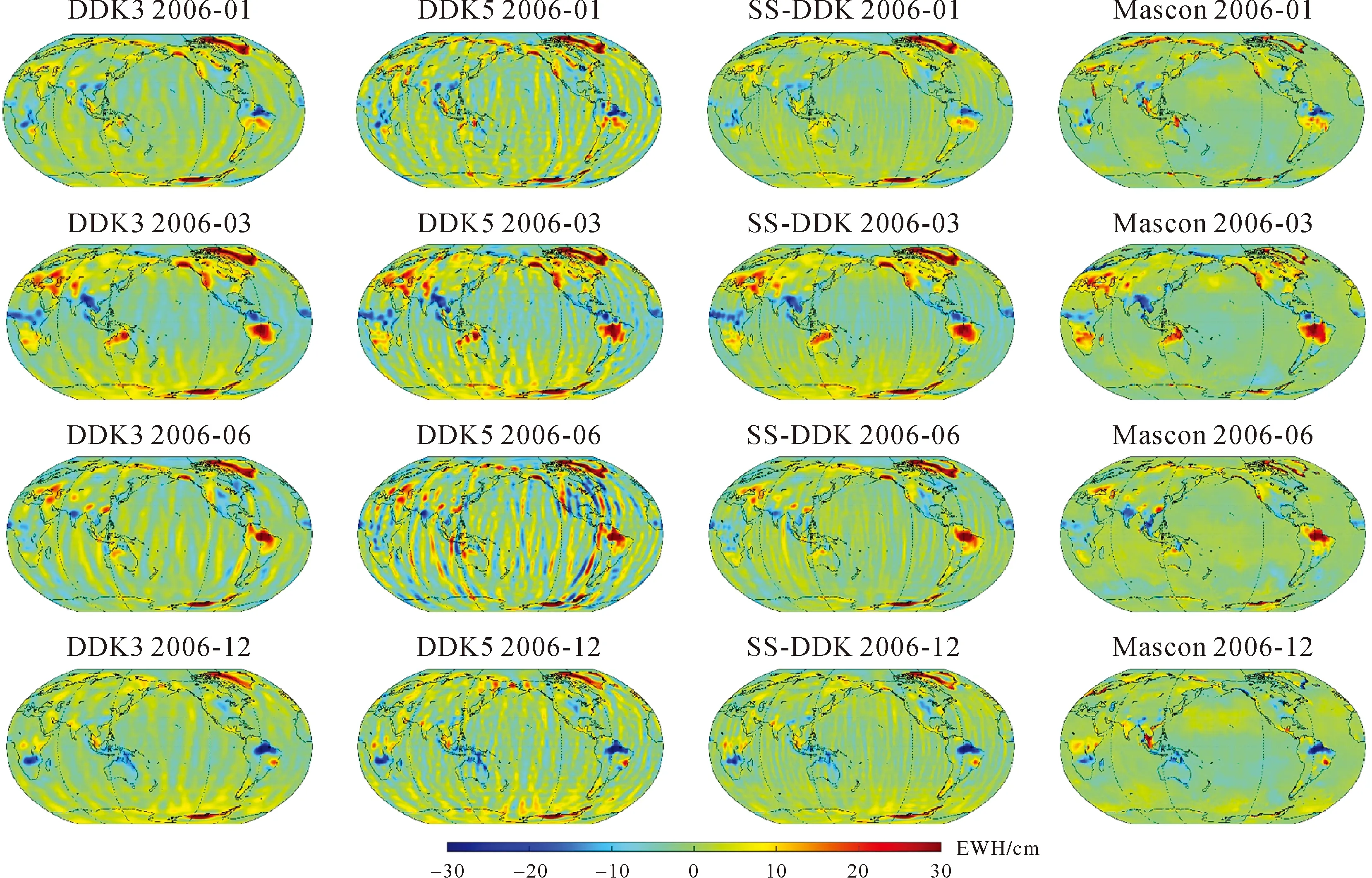
图3 2006年1、3、6和12月分别经DDK3、DDK5和SS-DDK处理后的结果及对应月份的mascon解

为更进一步地论证SS-DDK去条带和保留信号的能力,选取上述5个区域分别绘制区域整体的EWH变化的折线图(图5左侧一栏)以及与mascon解差异的折线图(图5右侧一栏)(绘图时忽略存在数据缺失的月份)[28]。在图5左侧一栏前4个区域,SS-DDK和DDK系列滤波结果与mascon解在整个时间段内符合地较好;在亚马孙河流域、刚果河流域和恒河流域部分月份,mascon解的振幅大于其余滤波解。从整个时间序列来看,无论哪一种解前4个区域的EWH都存在周期性变化。在格陵兰岛,SS-DDK和DDK1—8都与mascon解存在不同程度的偏离,这可能是由于信号泄漏所造成的,但SS-DDK与DDK系列滤波之间符合地较好。图5右侧一栏展示SS-DDK和DDK1—8与mascon解的差异,SS-DDK滤波解的质量异常差异(以mascon为参考)与DDK系列滤波解的质量异常差异相近,在部分区域的部分时间月份SS-DDK质量异常差异要小于任何一种DDK,但在亚马孙河流域和刚果河流域存在初始月份偏差较大的问题,可能由于滚动求解时第一年第一个月的约束解仅求解一次,导致SS-DDK滤波解在初始月份与mascon解的质量异常差异相较于DDK1—8滤波更大一些。

2.2 方差和协方差分析与不确定性估计

测量误差协方差矩阵R通常是不准确的,往往高估了数据的准确性。为解决这一问题,可以简单引入方差分量因子δ2来对协方差矩阵R进行缩放。因此,本文通常用δ2R来代替R来表征球谐数据误差的大小[29]。方差分量因子的估计公式如下

(21)

式中,p表示约束解中非零元素的个数;n表示方程数,球谐系数的最大展开阶数为60,由式(1)和式(2)可知,n=3717×2;p取3717。式(20)表征球谐系数变化与等效水柱高变化之间的转换关系,可简单缩写为

ΔH=gTx

(22)

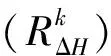
(23)

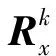
表2 SS-DDK和DDK2—5滤波在全球和区域的等效水柱高平均不确定度大小

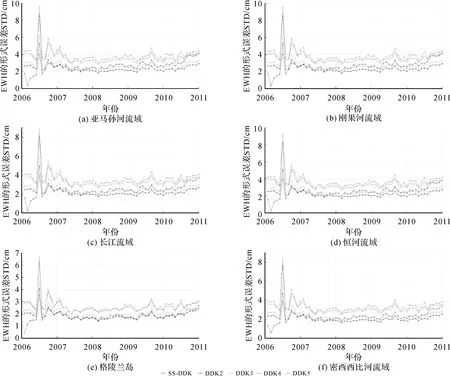
图6 6大区域SS-DDK和DDK2—5滤波解估计的等效水柱高不确定性随时间的变化

由图5—图6分析可知,SS-DDK估计的等效水柱高不确定性要小于DDK3—5滤波,但大于DDK2。综合考虑,SS-DDK解的不确定性大小介于DDK2和DDK3之间,与DDK3滤波最为接近。通过对比各约束解的不确定性大小,充分说明SS-DDK的去条带效果是可靠的。

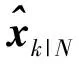
图7 经SS-DDK处理后2006—2011年等效水柱高全球格网点的平均不确定性

2.3 时间序列拟合分析

本文选用的GRACE观测时段是2002年4月至2014年6月(含缺失数据月份),反演135个月GRACE球谐系数的数据,并利用不同滤波方法(SS-DDK、DDK1—8)进行约束求解得到EWH。对全球范围内所有格网点的EWH采用线性拟合模型进行最小二乘拟合,得到线性年变化率、周年振幅及半周年振幅。线性拟合模型具体为[30]

ΔH=a0+a1(t-t0)+b1cos(ωt)+b2sin(ωt)+b3cos(2ωt)+b4sin(2ωt)+ε

(24)

式中,ΔH为等效水柱高变化;t为时变重力场模型时间(以年为单位);t0为参考时间;a0为常数项;a1为年变化率,表征EWH年变化快慢;ε为拟合残差;b1和b2的平方和开根号表示周年振幅(annual amplitude,AAMP);b3和b4的平方和开根号表示是半周年振幅;ω为频率。区域EWH变化的RMSD计算公式为

(25)

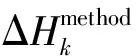
图8展示从2002年4月至2014年6月经滤波之后的周年振幅,考虑到无约束解中已经扣除非潮汐大气、高频海洋信号、各种潮汐的影响,所以海洋上信号的周年振幅恰好反映滤波方法的去条带水平。在海洋区域,SS-DDK方法的周年振幅低于DDK5—8滤波,与DDK3、DDK4最为相似;在信号较强的区域,如亚马孙河流域、刚果河流域、长江流域及恒河流域,SS-DDK的周年振幅与DDK系列滤波相比没有发现明显的条带误差。图9表示全球格网点的RMSD,SS-DDK与DDK3在误差水平上最为接近。从全球格网点的周年振幅和均方根来看,SS-DDK的去条带能力强于DDK1—2和DDK5—8。

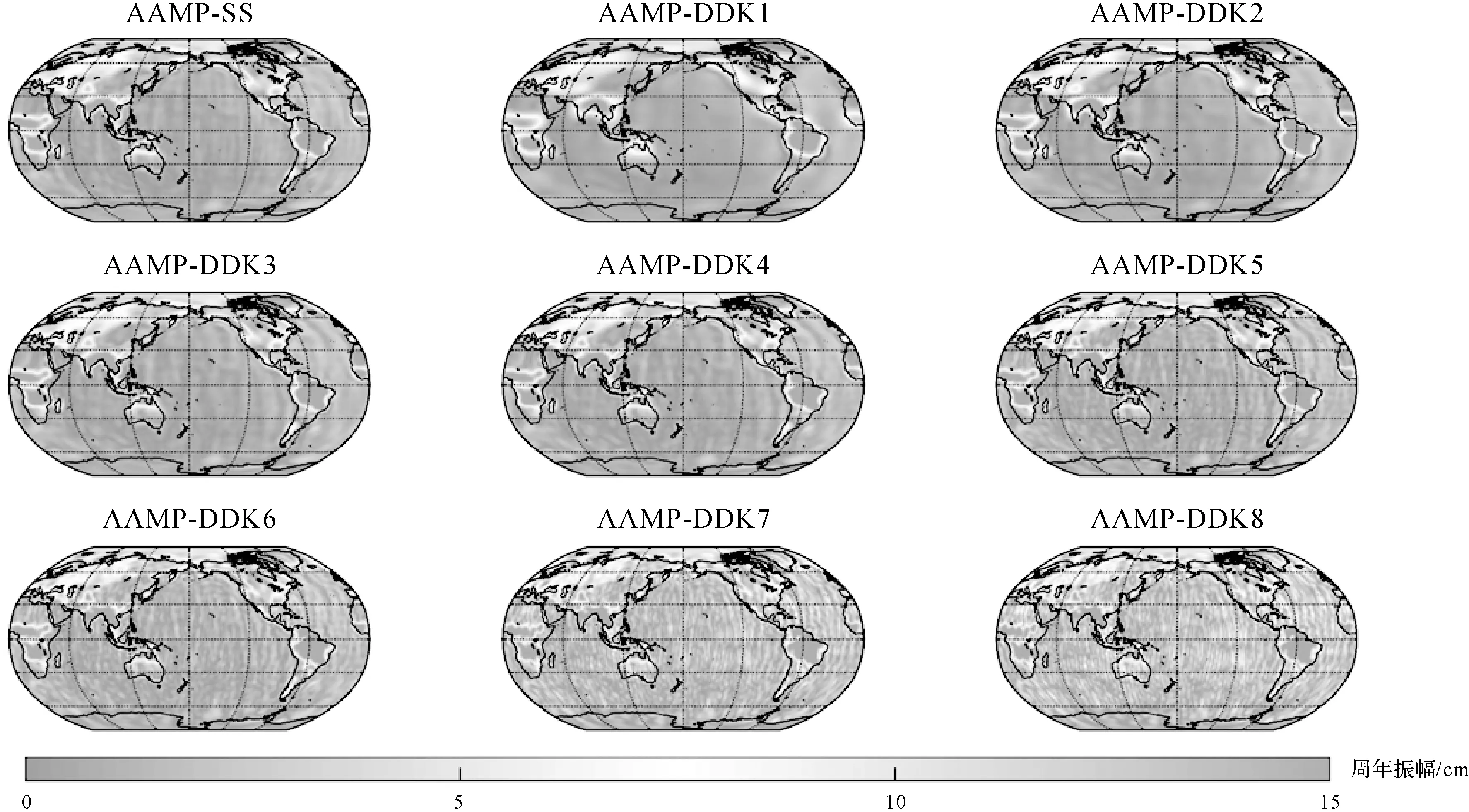
图8 2002年4月至2014年6月不同滤波方法EWH的周年振幅

图9 全球格网点2002年4月至2014年6月不同滤波方法EWH的RMSD

2.4 信号和噪声水平分析

重力场模型的精度可以用各阶大地水准面误差的平方和开根号来表示[31-32]

(26)

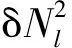
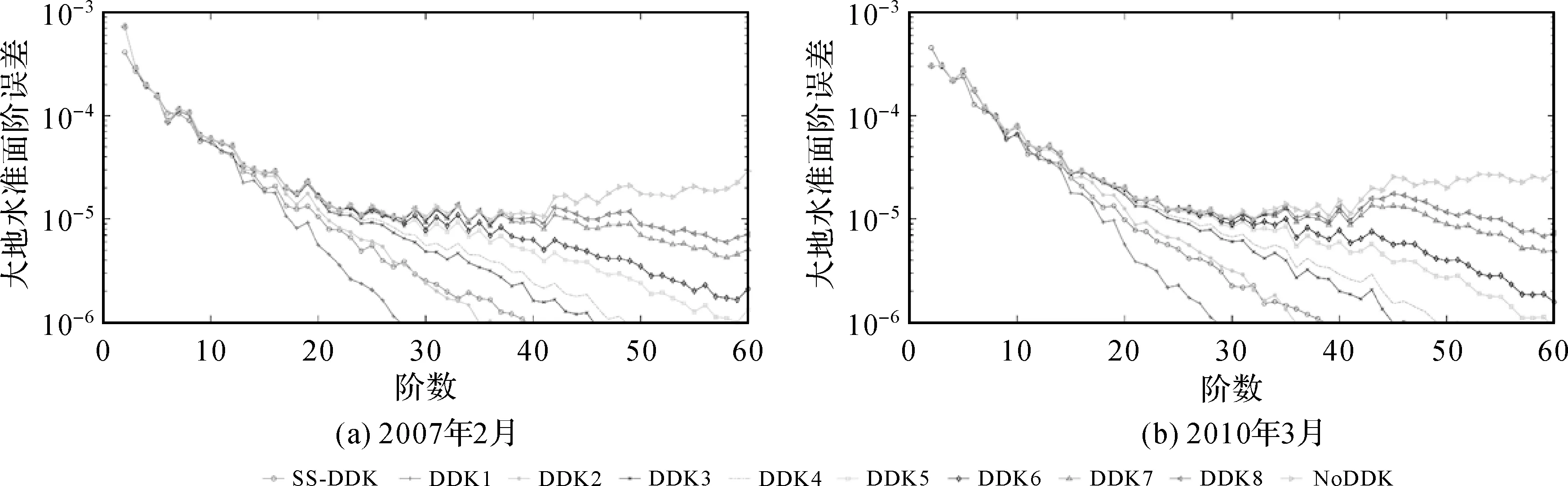
图10 各种约束解在2007年2月和2010年3月的大地水准面阶误差变化

2.5 仿真试验分析

由于实际地表质量变化的真值无从得知,无法更加客观地评价状态空间模型SS-DDK的去条带和保留信号的性能,故进行仿真试验,进一步说明SS-DDK性能的优劣。

假定CSR机构发布的RL06 v2.1 mascon解为对地表质量实际变化的真实反映,将mascon格网点质量转为最大阶数为60的球谐系数,人为在球谐系数中加入条带误差,分别利用状态空间SS-DDK和DDK2—5滤波进行处理得到1°×1°的等效水柱高全球格网图和区域等效水柱高时间序列差异图。具体操作如下:

(1) 利用CSR发布的mascon数据得到2006—2011年全球1°×1°的等效水柱高格网图作为真值,图11展示2009年上半年mascon的全球格网。

图11 2009年1—6月CSR RL06 v2.1 mascon解1°×1°等效水柱高全球格网

(2) 在mascon解转换得到的球谐系数中人为加入条带误差,误差的协方差矩阵已知,图12展示2009年上半年加入条带噪声之后的未滤波全球格网。

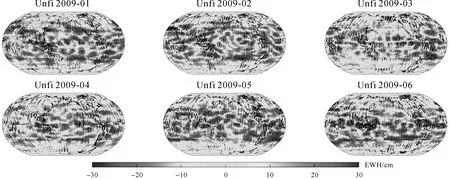
图12 2009年1—6月mascon解人为加入条带误差后1°×1°等效水柱高全球格网

(3) 用状态空间SS-DDK滤波对未滤波解进行处理,图13展示2009年上半年经SS-DDK滤波之后的全球格网。

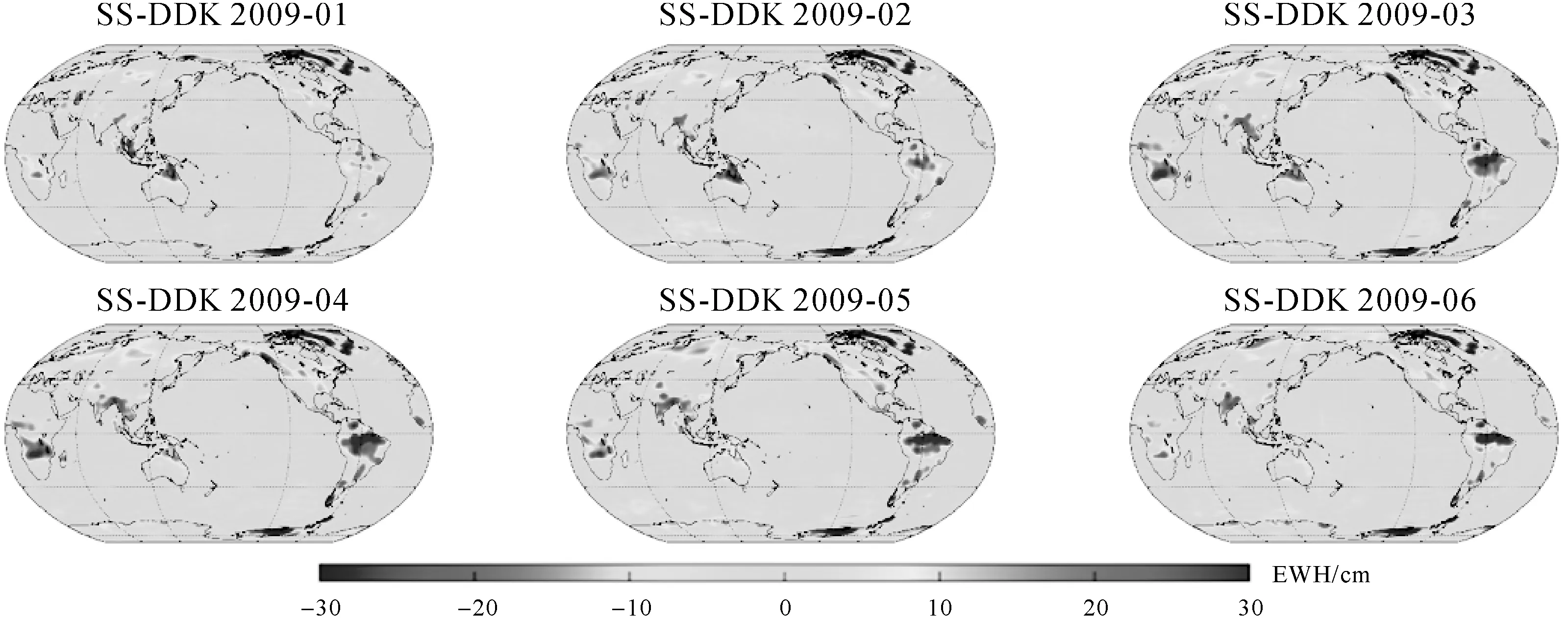
图13 2009年1—6月未滤波解经SS-DDK后1°×1°等效水柱高全球格网

(4) 分别用DDK2—5滤波处理未滤波解,将滤波结果和SS-DDK结果与mascon解(真值)进行比较分析,图14展示在亚马孙河流域、刚果河流域、长江流域及格陵兰岛区域各滤波解与mascon解的差异。

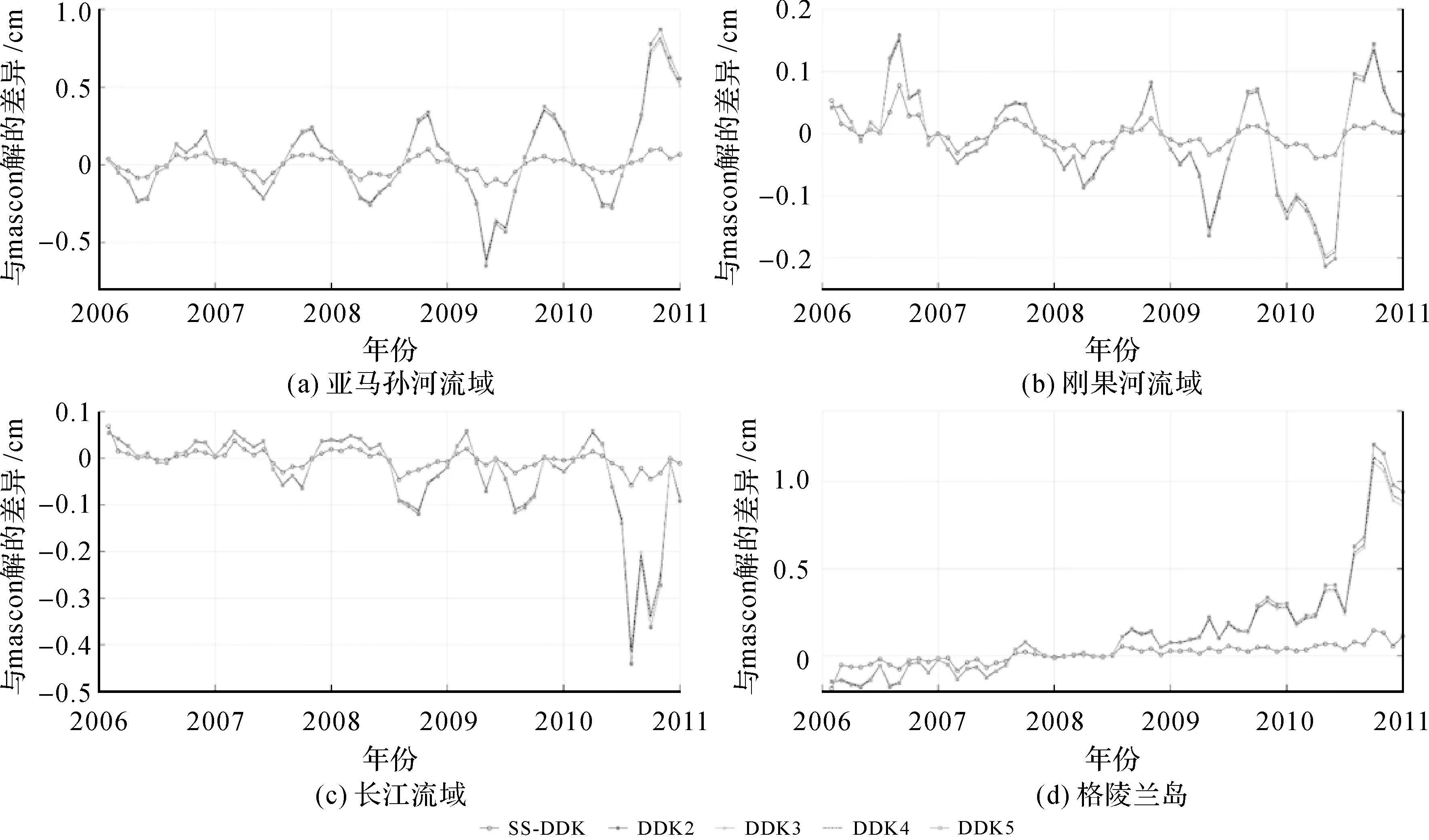
图14 SS-DDK和DDK2—5滤波解相对于mascon解(真值)在亚马孙、刚果、长江和格陵兰岛的等效水柱高差异

对比图11—图13不难发现,2009年上半年mascon解和SS-DDK解的等效水柱高全球格网图上,条带误差几乎被去除,SS-DDK解在亚马孙河、刚果河、长江和格陵兰岛等区域的信号与mascon解基本一致。对比4大区域2006—2011年未滤波解和各种滤波解与mascon解的差异发现,各滤波解与真值的差异都在0附近,且SS-DDK解的差异比DDK2—5解更小,说明经状态空间SS-DDK后的处理结果更加贴近真值。

3 结 论

本文提出一种状态空间模型方法,用于处理GRACE Level-2产品。该方法与传统状态空间法的区别在于:状态向量只包含球谐系数,而将GRACE Level-2中的协方差矩阵用作观测误差协方差矩阵;基于数据对过程噪声协方差矩阵的尺度因子(方差分量)进行自适应调整;采用平滑解而非滤波解作为最终的数据处理结果。

选取CSR发布的RL05 2002年4月至2014年6月的GRACE Level-2产品,得到经约束后的球谐系数和全球地表质量变化,并与DDK1—8滤波和CSR RL06 v2.1 mascon进行对比分析。分析结果表明:

(1) 分别绘制SS-DDK、DDK1—8及CSR RL06 v2.1 mascon全球范围的EWH图。对比发现在高纬度的格陵兰岛,SS-DDK与DDK3—8滤波都能保留更多的信号。在其他区域,例如亚马孙河流域,在2006年6月和12月前后,SS-DDK方法与DDK3、5滤波一样具有明显的等效水柱高(EWH)变化。对比不同方法全球所有网格点,SS-DDK的均方根最小为10.36 cm,即SS-DDK方法的去条带和保留信号的能力与mascon解最为接近。

(2) 从5大区域入手,绘制约束解和mascon解流域质量异常图以及各约束解与mascon解的质量异常差异图。在格陵兰岛,所有约束解均较大地偏离mascon解,且DDK系列滤波解的偏离均大于SS-DDK解,但各约束解之间符合地较好。在其他4个区域,各约束得到的时间序列图像都存在周期性变化;SS-DDK与DDK3—5有不同程度的相似,而且在某些时段SS-DDK方法的质量异常差异要小于任意一种DDK滤波解。

(3) 分析6大区域的不确定性时间序列图发现,SS-DDK估计的等效水柱高不确定性要小于DDK3—5滤波,但大于DDK2滤波,综合考虑全球和各个区域的平均不确定度大小可知,SS-DDK估计结果的不确定度介于DDK2和DDK3滤波之间。需要说明的是,试验中发现整个时段数据连续处理效果不佳,每5年(60个月)为一个单位进行整体处理最为合适,能够充分顾及球谐系数的误差特性。

(4) 对不同约束解和mascon解135个月的EWH进行线性模型拟合,求解流域RMSD和年振幅,并绘制全球格网点图像。进一步说明SS-DDK解在格陵兰岛的均方根最小,存在更少的信号失真。在海洋区域,SS-DDK解的年振幅低于DDK5—8,与DDK3—4较为相近;在强信号区域,SS-DDK解不存在明显的条带误差;SS-DDK与DDK3在误差水平上最为接近。

(5) 从不同约束解的大地水准面阶误差来看,SS-DDK解中噪声水平低于DDK4—8,保留信号的能力与DDK2—3解相当。

(6) 增添仿真试验发现SS-DDK解与mascon解(真值)的差异相较于DDK系列滤波更加接近,更加充分说明SS-DDK方法在去条带和保留信号方面具有较好的性能。

后续研究中可以尝试使过程噪声协方差矩阵的方差分量参数随月份变化,以反映不同时间处信号变化幅度不一致的现象,这需要对方差分量进行逐月调整。