基于电磁信息论的多用户超大规模MIMO的互信息研究
2023-12-15虢周卓许柏恺肖华华章嘉懿
张 寅,虢周卓,王 者,许柏恺,肖华华,章嘉懿
(1.北京交通大学 电子信息工程学院,北京 100044;2.中兴通讯股份有限公司,广东 深圳 518057)
0 引言
近年来,随着大规模多输入多输出(Massive MIMO)技术的广泛使用,移动通信系统的性能不断提高。超大规模多输入多输出(Extremely Large-scale MIMO,XL-MIMO)提供了巨大的空间自由度,有望成为6G关键技术之一[1-2]。但随着收发天线数目不断增加,如何处理XL-MIMO天线孔径有限的性能限制[3]成为当下亟待解决的问题。连续孔径MIMO(Continuous-aperture MIMO,CAP-MIMO)[4-6]是解决该问题的可能技术路线之一。与传统由多个天线组成的离散XL-MIMO[7-9]不同,CAP-MIMO作为一种具有无限密集天线的MIMO结构,也被称为全息MIMO[10-11]、超大规模智能超表面(Large Intelligent Surface,LIS)[12-13]和可重构智能超表面(Reconfigurable Intelligent Surface,RIS)[14-15],由于其空间连续的电磁结构[3],能产生任意的电流分布,被接收机接收的信号可以在空间电磁波上进行调制,因而有望突破有限孔径的性能限制[6]。
对于XL-MIMO系统,主流分析和设计过程通常基于白噪声、标量、远场、离散化、单色和其他非物理一致的假设。但考虑连续孔径XL-MIMO,这些假设将不存在。因而,需要找到一套适用于连续孔径XL-MIMO的分析方法,文献[6]提出了一种通用的分型复用技术,将连续模式函数的设计转化为在有限正交基上的投影长度设计来解决和速率最大化问题。但文献[11]并未考虑到随着天线数量的增加,在每个天线上观察到的噪声将表现出两种不同的特性。
针对天线数目增加导致的噪声特性变化问题,已有相关研究将噪声分解为白噪声分量和非白噪声分量,并对噪声进行随机场建模,建立起连续孔径XL-MIMO的分析方法[16]。但其讨论的情况仅限于单用户通信系统,并未进一步探究更一般的多用户通信场景。
基于此,本文基于利用连续孔径XL-MIMO的分析方法建立起多用户情景下的连续孔径XL-MIMO系统,考虑了由天线数量增加所导致的噪声特性变化,并进一步探究了模型的适用范围。具体做了以下工作:
① 建立了多个连续区域之间无线通信的系统模型,得到系统传输的目标函数。
② 利用随机场对系统进行了相关建模,推导出基于电磁信息论的多用户连续孔径XL-MIMO的互信息表达式以及简化的数值计算方法。
③ 基于互信息表达式以及数值计算方法,分别讨论了不同噪声场景下,多用户连续孔径XL-MIMO系统的准确互信息。分析了离散点数、白噪声功率、非白噪声功率等因素对互信息的影响,进一步探究了其适用场景,分别对波长、噪声功率与互信息收敛时最大离散点数之间的关系进行了研究。
1 多用户XL-MIMO系统模型
基于电磁信息论,麦克斯韦方程组揭示了收发器间信息的传输过程,同时格林函数建立起了发射端电流密度与接收端感应电场强度之间的关系。
考虑两个任意连续区域Vs和Vr之间的通信模型[13]。源端电流密度为J(s),接收端产生的感应电场为E(r),利用格林函数,其电场E(r)为:
(1)
根据文献[17],在无界均匀介质中,固定频点的格林函数为:
(2)

1.1 系统模型
考虑一个如图1所示的多用户连续MIMO无线通信系统,它包括了一个接收端,一个源端以及K个干扰端。其中,收发器天线均为连续孔径的链式阵列天线。
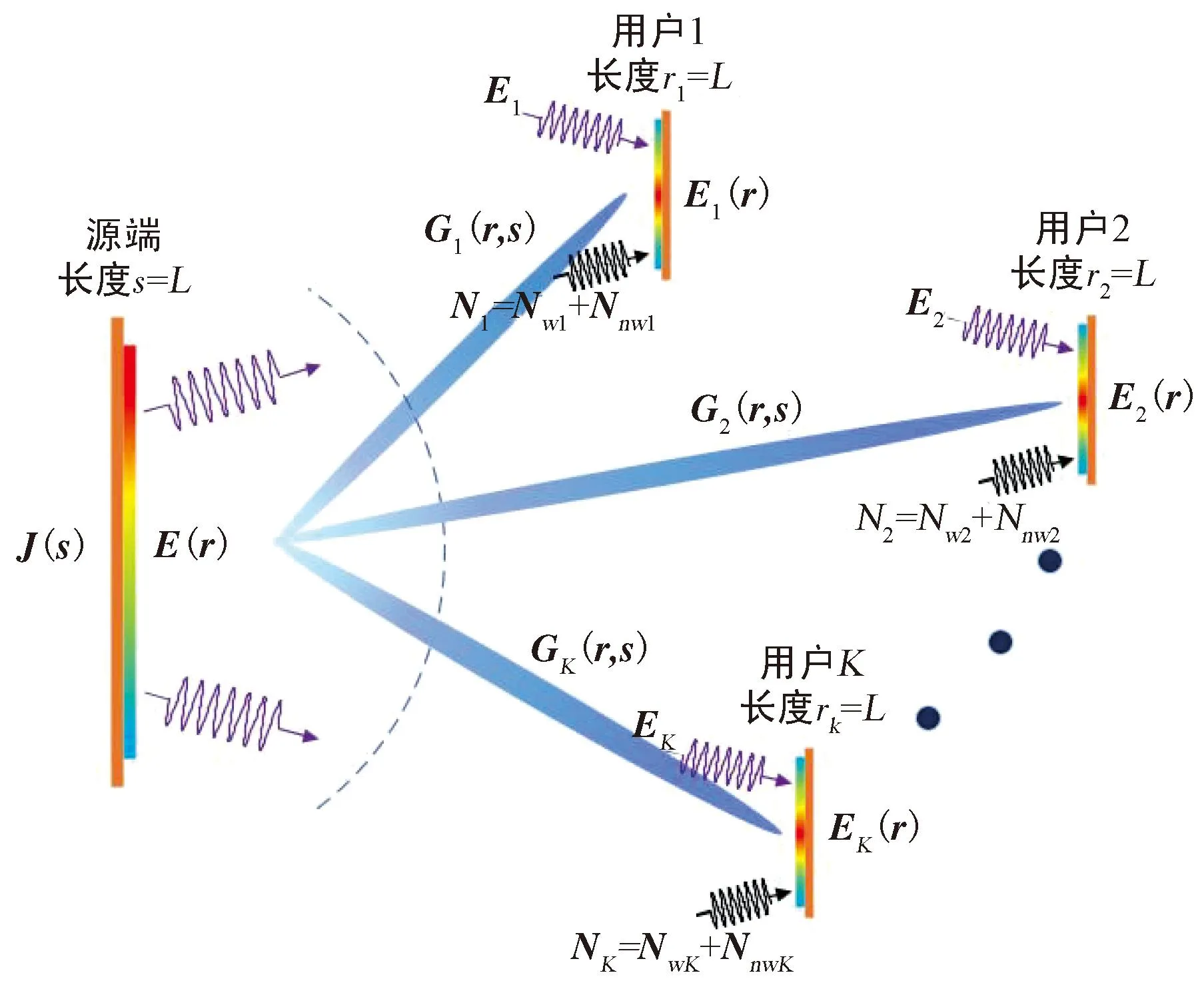
图1 多用户XL-MIMO系统简化模型Fig.1 Simplified model diagram for Multiuser XL-MIMO system
源端的电流密度为J(s),接收端的感应电场为E1(r),在理想情况下,期望接收器能够理想地捕获到达点d1的电磁波全部信息。由式(1)知,接收端捕获到的电场信号为:
(3)
式中:E1为期望信号产生的电场,Ej为干扰信号产生的电场,N1为噪声场。
1.2 基于随机场的信号建模
根据电磁信息论,本文分析基于Shannon随机模型,因此需要利用随机场对信号进行建模。随机场反映了无线通信系统的统计特性,而在所有种类的随机场中,高斯随机场具有理论意义,因此用它描述源端电流密度以及接收端电场强度的统计特性。假设高斯随机场为连续、可离散的,其可以由均值以及自相关函数来表示高斯随机信号的特征。
因此,假设源端电流密度和接收端电场强度均符合高斯随机场特性,可得:
(4)
由式(1)可得:
RE1(r,r′)=[E1(r)E1H(r)]=
(5)
1.3 基于随机场的噪声建模
本节将对噪声进行随机场的建模。通信系统中,噪声一般分成白噪声分量与非白噪声分量,白噪声分量一般考虑到通信系统中的非理想因素,这种影响呈现空间的不相关性,因此利用加性高斯白噪声(AWGN)来描述这一分量。
(6)
对于非白噪声分量,可以将其视作非源端电流产生的入射电磁波的叠加。根据文献[16],非完全各向同性的辐射干扰的随机场自相关函数为:
(7)
式中:κ为波矢量,f1和f2为辅助函数,其具体定义如下。
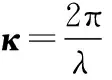
(8)
至此得到了系统模型,信号和噪声的随机场模型,下一节将根据所建模型进行互信息公式的推导。
2 多用户连续XL-MIMO系统互信息及数值计算
2.1 系统互信息
为得到互信息的表达式,考虑基于平行有限长度线性收发天线的多用户XL-MIMO系统。根据电磁信息论,可得J(s)与E1(r)、Ek(r)之间的关系,可用式(2)中矩阵G左上角的元素G1.1来描述,可推导为:
(9)
式中:x=r-s,d为收发器之间的距离。
因此,进一步得到了源端电流密度与接收端感应电场之间的关系:
(10)
接收电场的自相关函数为:
(11)
利用文献[16]提及的方法,可以将Ej(r)、Y(r)和N(r)进行Mercer展开:
(12)
可以构建两个空间H1和H2,分别由ξE1,k和ξY,k展开,E1(r)和Y(r)之间的互信息为空间H1和H2之间的差值。
可得这个空间的差值,即E1(r)和Y(r)之间互信息可以由范德蒙行列式的算子来求得:
(13)
式中:TY为Y(r)自相关函数的积分算子,TE1为E1(r)自相关函数的积分算子,TD和TD′分别是与E1(r)和Y(r)相互关联的算子。
此处,类比地假定噪声场N与期望电场E1无关,由于假定期望信号与干扰信号无关,干扰电场与期望电场无关,同样可以得到TD=TD′=TE1。
将其代入,进一步化简互信息表达式为:
(14)

(15)
2.2 数值计算
根据文献[16]中算法1,可以得到互信息的公式:
(16)
式中:
(17)
至此完成了多用户XL-MIMO系统模型的数值计算,为接下来的仿真提供了基础与依据。
3 仿真分析
为简化讨论,考虑一个接收端,一个用户端,一个干扰端的情况,且三者互相平行,中心点都在同一直线上,如图2所示。
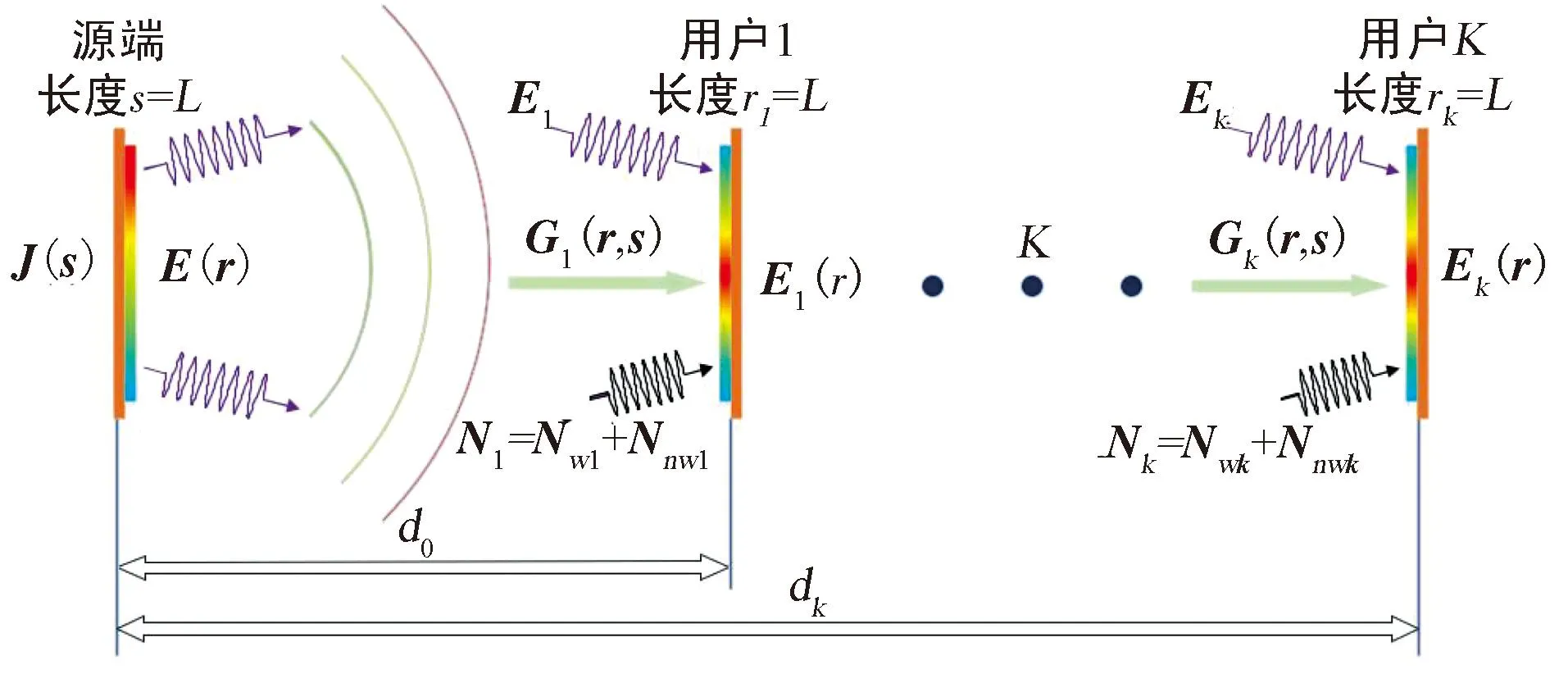
图2 K=2时具体仿真情景Fig.2 Specific simulation when K=2
3.1 不同种类噪声情景
基于前文中对白噪声情景下考虑干扰情况的多用户XL-MIMO通信系统互信息表达式的求解以及数值计算,首先在仅考虑白噪声的场景下进行仿真,进一步再扩展为非白噪声场景。
3.1.1 白噪声情况相关仿真
为简化讨论,将干扰端的个数设为1,同时假设收发器间距均为1 m,长度均为2 m,信号波长为0.25 m,基于上述条件,讨论离散点数、白噪声功率对互信息值的影响,如图3所示。

图3 白噪声情景下K=2的MIMO系统Fig.3 MIMO system with K=2 in white noise context
为了与单用户的情况进行对比,绘制单用户情况下对应曲线,如图4所示。

图4 白噪声情景下K=1的MIMO系统Fig.4 MIMO system with K=1 in white noise context
通过对比,在白噪声情景下K=2时,多用户XL-MIMO系统互信息的值会因干扰的加入出现明显下降,同时互信息的值随白噪声功率减小而增大,当白噪声功率小于10-7V2/m2时,连续接收端(36点离散)获得的信息对比半波离散点数(16点)离散接收端获得的信息有着明显提升。
对比单用户MIMO模型,连续接收端获得的信息仍在白噪声功率为10-10V2/m2时相比半波离散化接收端有着19.49%的提升,相比8点波长离散化接收端获得的信息有138.9%的提升,说明了连续接收端在通信系统存在干扰时相较于离散接收端能获得更多的信息。
3.1.2 非白噪声情况相关仿真
为了进一步研究多用户XL-MIMO系统,将白噪声的场景推广到非白噪声的场景。
简便起见,在此处也将干扰端的个数设置为1,依旧假设收发器间距均为1 m,长度均为2 m,信号波长为0.25 m,在考虑非白噪声的场景下,固定非白噪声功率为0.5 V2/m2,来讨论离散点数,白噪声功率对互信息值的影响,如图5所示。
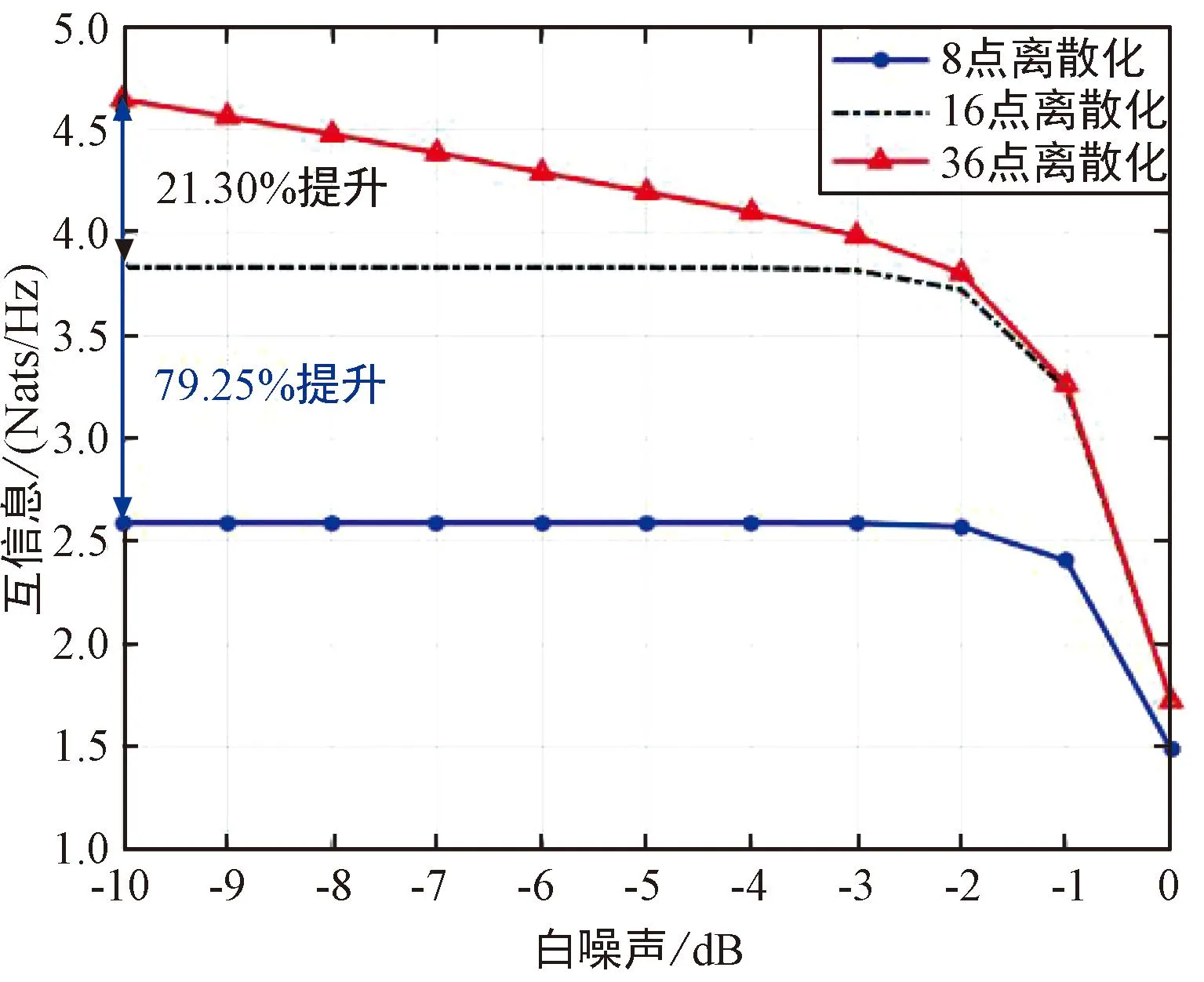
图5 非白噪声情景下K=2的MIMO系统Fig.5 MIMO system with K=2 in non-white noise context
为与单用户的情况进行对比,绘制了非白噪声情景下单用户MIMO系统的对应曲线,如图6所示。
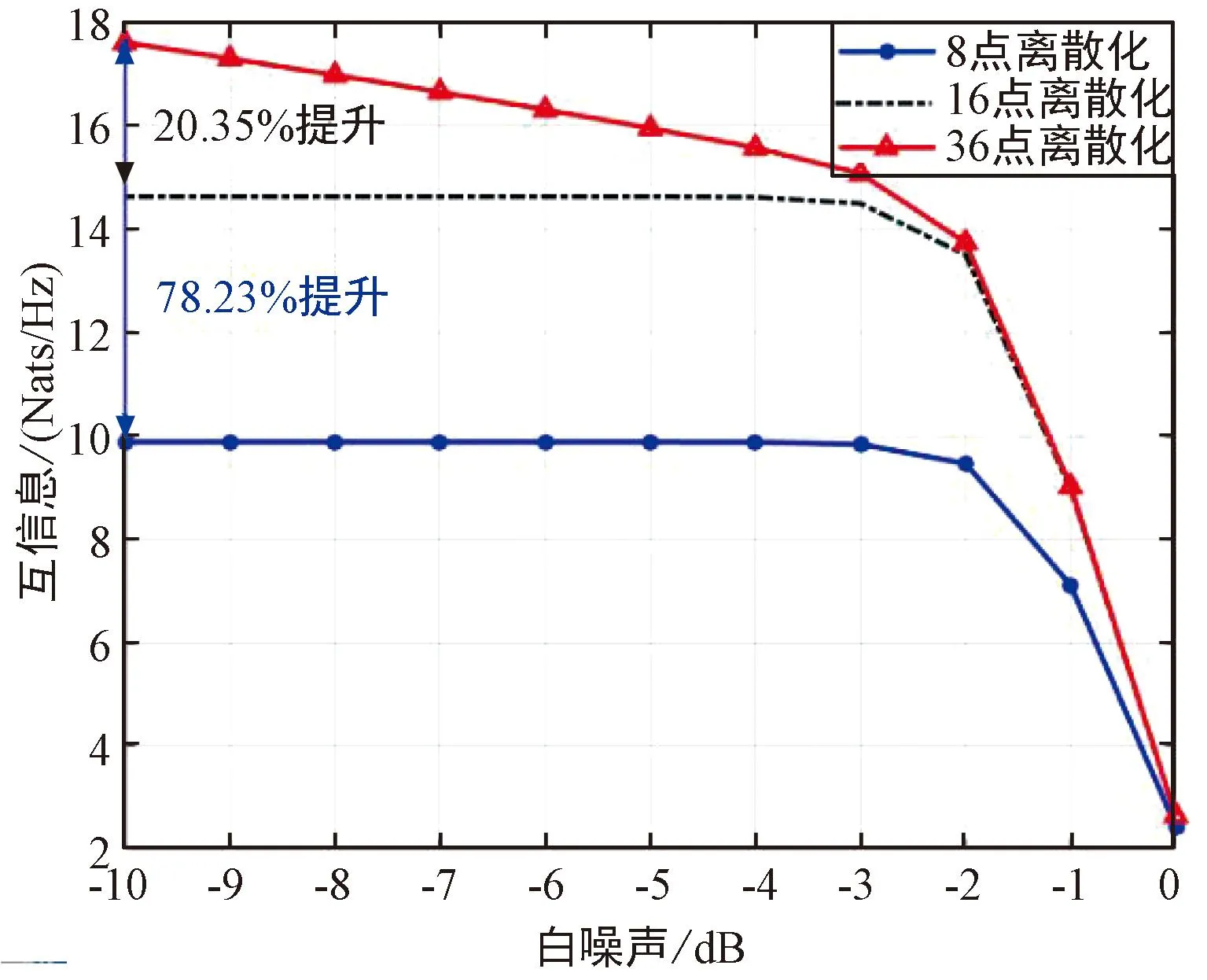
图6 非白噪声情景下K=1的MIMO系统中Fig.6 MIMO system with K=1 in non-white noise context
通过对比,在非白噪声场景下,K=2的多用户XL-MIMO系统中,互信息的值会因为干扰的加入出现明显下降,互信息的值随白噪声功率减小而增大,当噪声功率小于10-3V2/m2时,连续接收端(36点离散)获得的信息对比半波离散点数(16点)离散接收端获得的信息有着明显提升。
此情况下,对比单用户MIMO模型,在白噪声功率为10-10V2/m2时,连续接收端获得的信息仍比半波离散化接收端有着21.30%的提升。
因此,在白噪声与非白噪声场景下,连续接收端获得的信息均比离散接收端有较大提升,且此类提升随着用户数量的增加而不断提高。
3.1.3 不同功率非白噪声的影响
为进一步探讨非白噪声功率值对于所假设模型互信息值的影响,将非白噪声功率进行更改以对实验进行了进一步的探究。
首先,将噪声功率分别设置为0.25、0.5、0.75、1 V2/m2以探究非白噪声功率在相同的量级发生变化时,对假设的通信模型互信息值的影响,如图7所示。

(a) 非白噪声功率
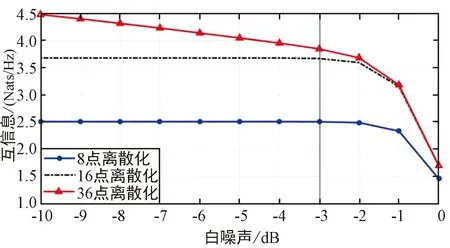
(b) 非白噪声功率

(c) 非白噪声功率

(d) 非白噪声功率
通过对比,当非白噪声功率在相同的量级发生变化时,相关的曲线走势并未发生明显变化。同时,在非白噪声功率发生量级不变的变化时,图中黑线表征的连续接收端(36点离散)相比半波离散点数(16点)离散接收端获得信息提升情况明显,其对应的白噪声功率不发生明显变化,即白噪声功率与非白噪声功率之比不发生明显变化。
进而探讨当非白噪声功率发生量级变化时,即当非白噪声功率与白噪声功率发生明显变化时,连续接收端较传统离散接收端获得信息有明显提高时对应的白噪声功率是否会发生变化。将噪声功率分别设置为1、10-2、10-5、10-10V2/m2以探究不同非白噪声功率的影响,如图8所示。
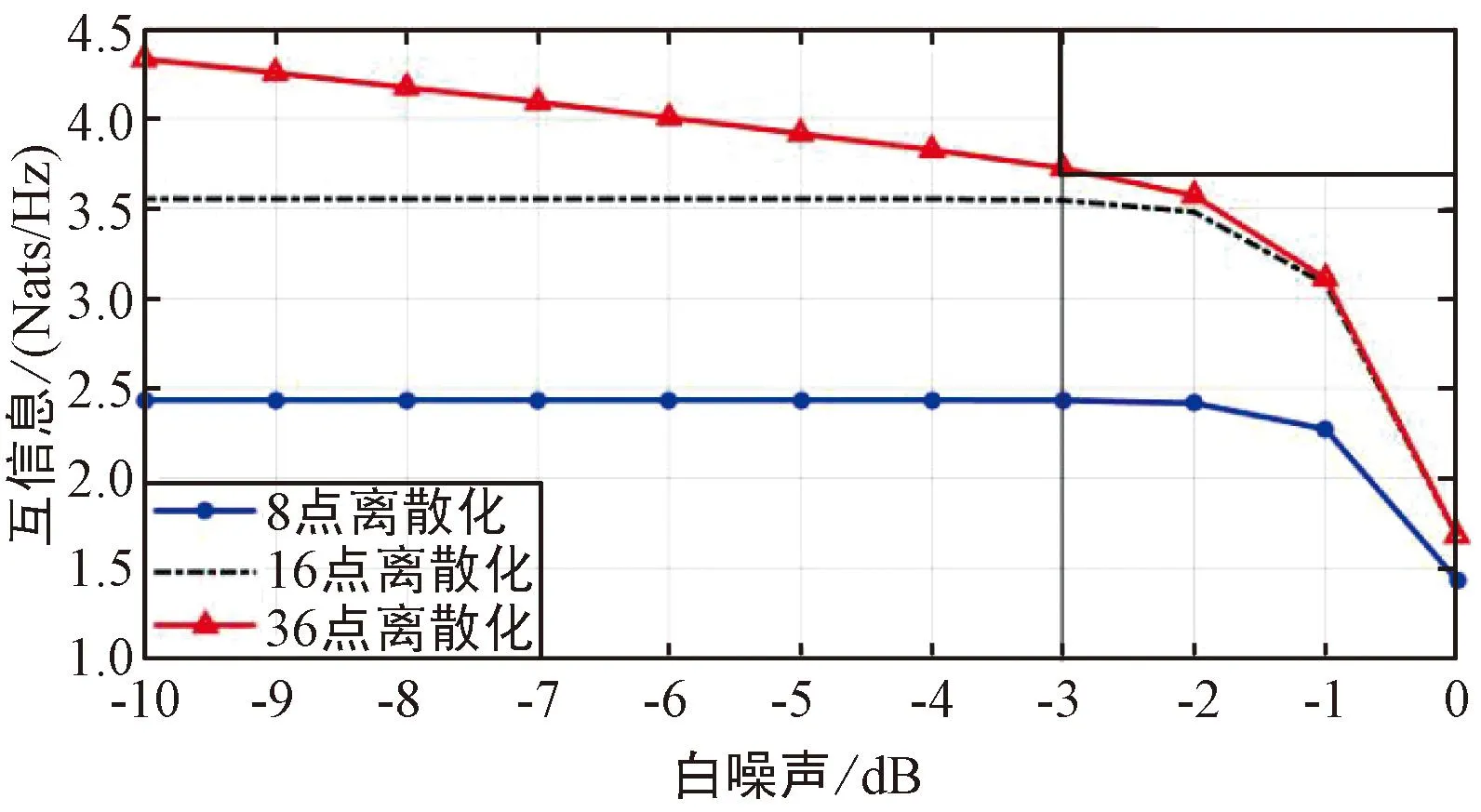
(a) 非白噪声功率

(b) 非白噪声功率
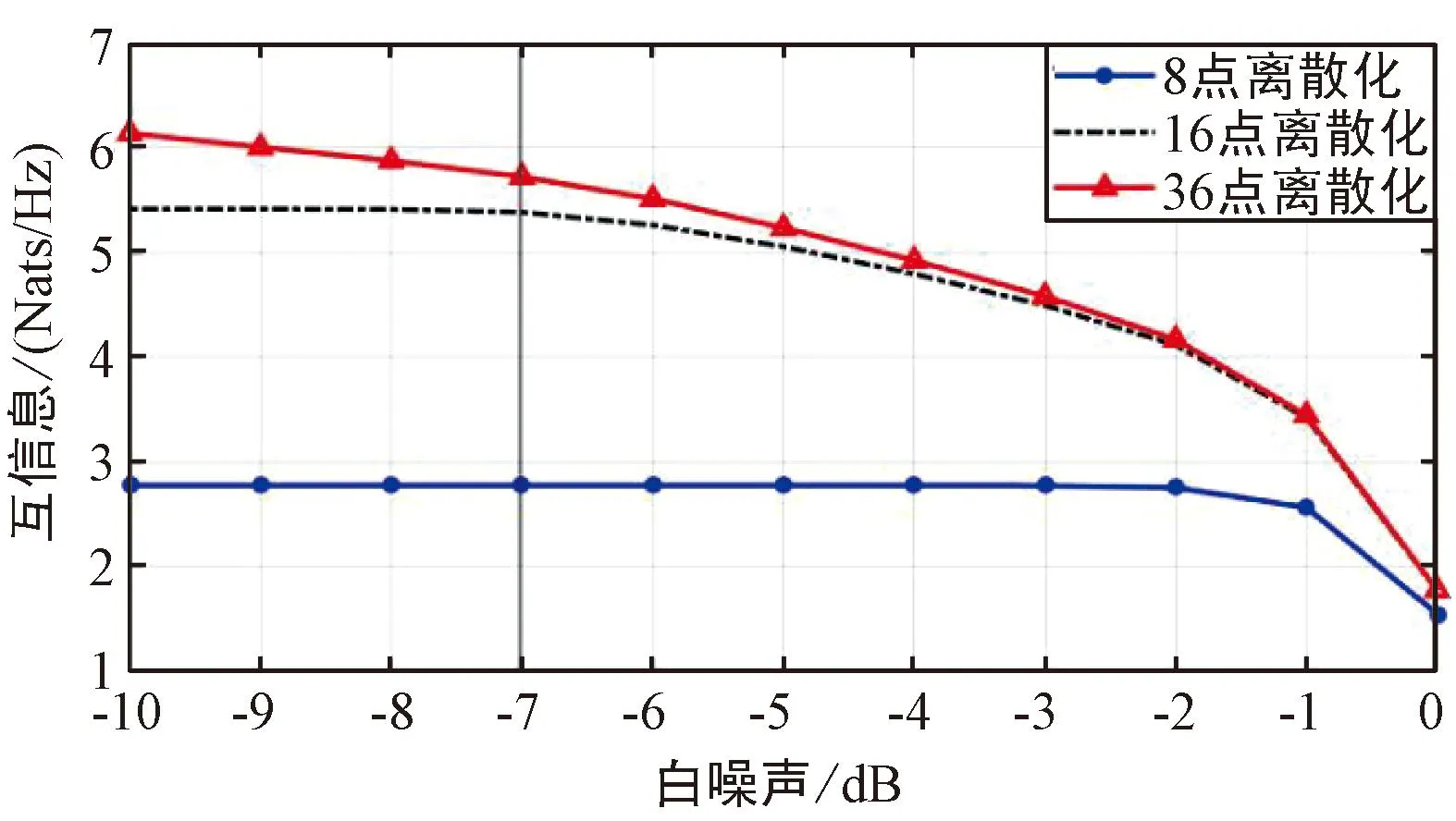
(c) 非白噪声功率

(d) 非白噪声功率
结果表明,当非白噪声功率在不同的量级发生变化时,相关的曲线变化较为明显。同时,在非白噪声功率量级变化时,连续接收端较传统离散接收端获得信息有明显提高时对应的白噪声功率发生明显变化,白噪声与非白噪声功率比约为1%,但当非白噪声过小时,噪声中非白分量可忽略,其仿真图与仅考虑白噪声时探究非白噪声功率、离散点数、白噪声功率对互信息影响的仿真图曲线趋势相近,如当非白噪声功率为10-10、10-5V2/m2时,曲线与图3 相似。
3.2 多用户情况下用户距离的影响
为简化操作,假设用户距离发生变化,收发器长度均为2 m,信号波长为0.25 m,在仅考虑白噪声以及考虑非白噪声两种情况下,探究端到端距离对于连续接收端获得的信息相比传统离散接收端获得信息的提升值的影响。其中,考虑非白噪声情况时,假定白噪声功率σ12为10-10V2/m2,非白噪声功率σ22为0.5 V2/m2,如图9所示。
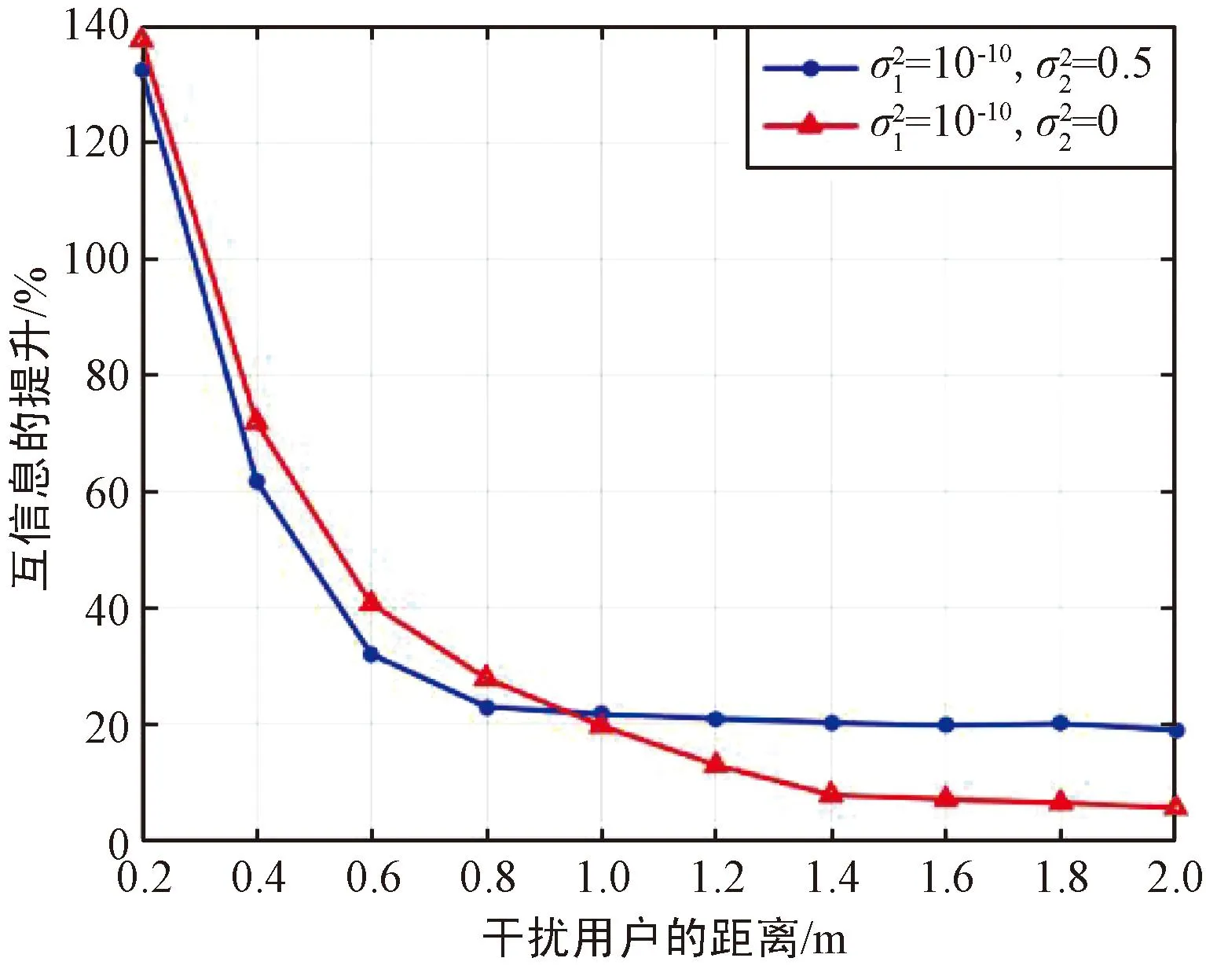
图9 K=2时端到端距离变化的影响Fig.9 Impact of end-to-end distance on mutual information improvement when K=2
由图9可以看出,无论是仅考虑白噪声或考虑非白噪声场景,连续接收端较传统离散接收端获得的信息均有提升,互信息提升程度会随端到端距离的减小而增大。此外,当端到端距离小于0.95 m时,连续接收端互信息相对于离散接收端的提升不小于20%。
但当噪声非白分量为零的情况下,随端到端距离的增大,连续电磁场互信息的提升逐渐不明显。
3.3 连续接收端离散点界限探究
本文采用离散的方式来逼近连续,从而达到分析连续接收端的目的。在文献[18]中,当接收天线数量在一定的孔径范围内无限增加时,会导致互信息发散的情况。其原因是当天线数量不断增大时,所假定的不相干噪声出现了空间的相干性,进而有信号能量呈二次缩放。而噪声能量呈线性缩放,信噪比得到无界的线性提高,导致容量发散到无穷大。因此,在满足互信息收敛的情况下,如何得到离散点数最大值是一个值得探讨的问题。
为了探究影响满足互信息收敛的最大离散点数的因素,初步探究了多用户连续MIMO模型下波长、噪声功率、收发器长度与互信息收敛时对应的最大离散点数之间的关系。
假设收发器间距均为1 m,收发器长度从1 m开始,以0.5 m为步进发生变化,波长分别为0.125、0.25、0.5 m。在仅考虑白噪声的情况下,先固定白噪声功率为10-10V2/m2,基于前文得到的仅考虑白噪声情况下K=2时多用户XL-MIMO系统互信息值数据计算过程,进行互信息收敛时最大离散点数的遍历寻找,将所得的最大离散点数与收发器间距进行线性拟合,以此来探究收发器距离与最大离散点数之间的关系,结果如图10所示。
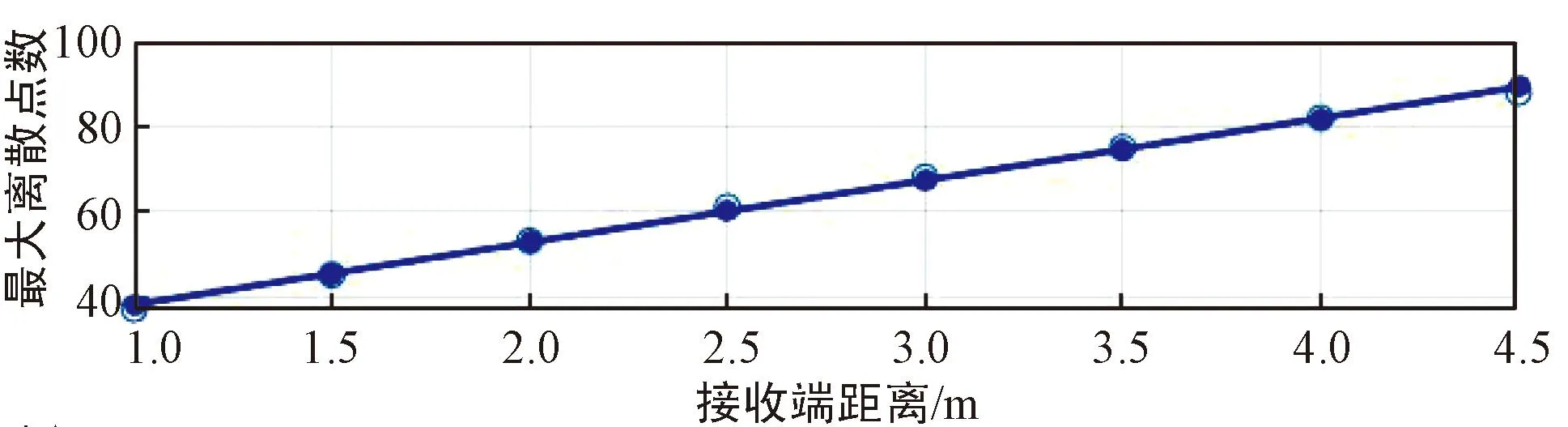
(a) λ=0.125 m
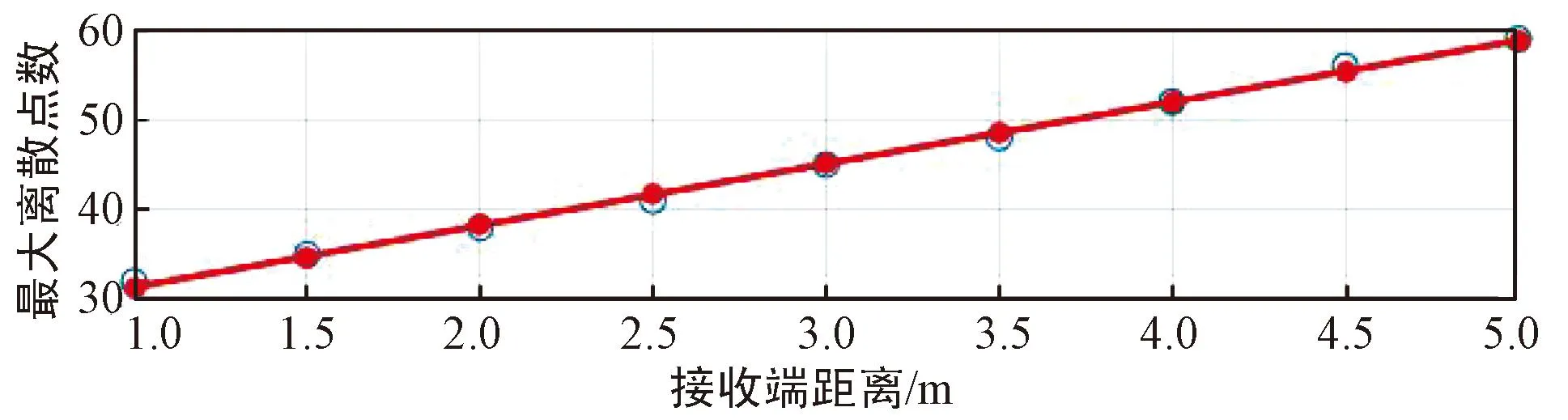
(b) λ=0.25 m

(c) λ=0.5 m图10 K=2时不同波长下,收发器长度对最大离散点数的影响Fig.10 Effect of transceiver length on the maximum number of discrete points at different wavelengths,K=2
由图10可得,若仅考虑白噪声场景,在不同波长下,收发器长度与最大离散点数之间成线性关系,同时,随波长减小频率增加,收发器长度对最大离散点数的影响更加明显。
在文献[16]提到的模型以及相关假设下,设置相同的条件,即K=1,收发器距离为1 m,连续收发器长度从1 m开始,以1 m为步进发生变化,波长分别为0.125,0.25,0.5 m,同样将所得的最大离散点数与收发器间距进行线性拟合,结果如图11所示。

(a) λ=0.125 m

(b) λ=0.25 m
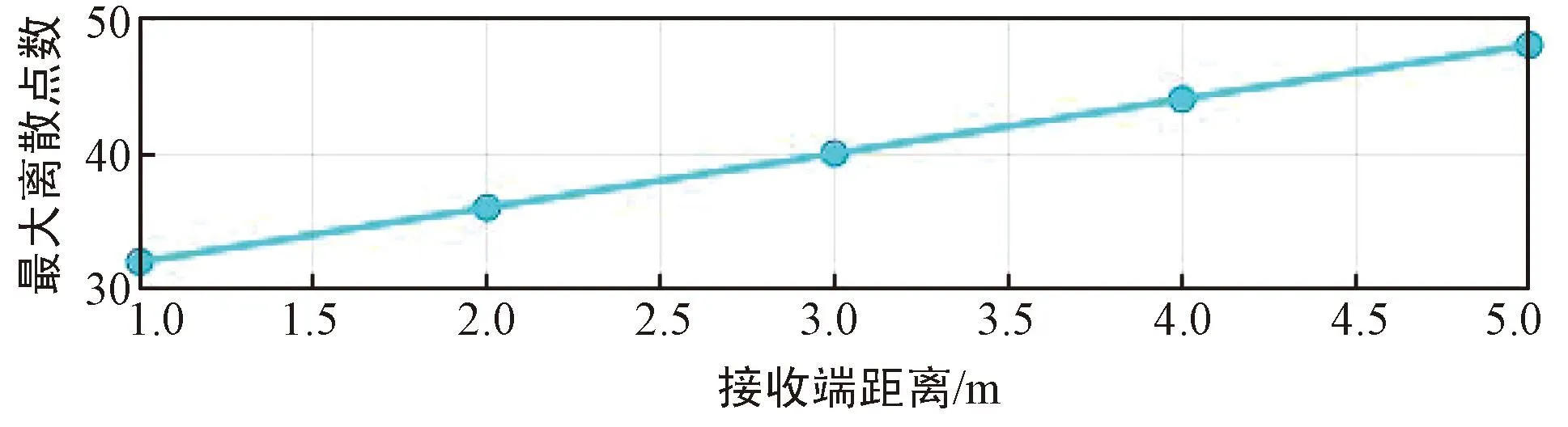
(c) λ=0.5 m图11 K=1时不同波长下,收发器长度对最大离散点数的影响Fig.11 Effect of transceiver length on the maximum number of discrete points at different wavelengths,K=1
由图11可知,单用户MIMO系统中收发器长度与最大离散点数仍然满足线性关系,同时,在单用户情况下,收发器长度对最大离散点数的影响随波长减小而增加。
由结果分析得,无论是在单用户还是多用户情况,当仅考虑白噪声场景时,在不同波长下,收发端长度与最大离散点之间近似成线性关系,且随波长减小,收发器长度对最大离散点数的影响更加明显。这对今后基于连续接收端分析互信息值相关模型中,寻找合适的最大离散点数具有参考作用。
4 结束语
本文考虑了多用户XL-MIMO系统特性,将多用户连续MIMO系统与单用户连续MIMO系统、多用户离散XL-MIMO系统进行比较,进而得到在不同噪声情景下,多用户XL-MIMO系统中,互信息同样会随着离散点数的增大而趋近于一个固定值。当噪声的非白分量与白噪声分量比值大于100时,连续接收端和互信息相比于传统半波离散接收端有着明显提升。在不同噪声情景下,连续接收端相较于离散接收端的优势会随着用户距离的减小更为明显。仿真结果发现满足互信息收敛的接收端最大离散点数与收发器长度具有明显的线性关系,这种线性关系不受信号频率、噪声功率的影响。未来的工作可以考虑更一般的天线阵列形态及多用户的随机分布场景。
