地下连续墙-桩组合基础的水平承载性能

2023-12-15张伟张兴丽陈逸飞魏焕卫刘聪

科学技术与工程 2023年33期

张伟, 张兴丽, 陈逸飞,3, 魏焕卫, 刘聪,4*

(1. 山东电力工程咨询院有限公司, 济南 250031;2. 山东建筑大学土木工程学院建筑结构加固改造与地下空间工程教育部重点实验室, 济南 250101;3. 山东省建筑工程质量检验检测中心有限公司, 济南 250031; 4. 大连理工大学海岸与近海工程国家重点实验室, 大连 116024)

随着城市建设不断发展,越来越多的工业建筑、电厂建筑及海洋建筑等在持续兴建的进程中也面临着诸多的问题。在工业与电厂建筑中,如存储大规模物质的仓库、电厂特殊工业锅炉房、火力发电厂的堆煤棚、冶金工业厂房和机械厂房的铸造车间等,因堆载需求所产生的较大水平力可能引起建(构)筑物基础发生侧向变形[1-2];与之相似的,在海洋建筑中,如海上石油钻井平台、风力发电机等,基础结构也往往受到波浪力、地震力等水平力作用[3]。

目前抵抗水平力的常规基础形式主要为群桩基础和地下连续墙[4-6],其中水平受荷桩作为承担水平力的主要构件形式是应用最为广泛的。常规提高群桩基础水平承载力的方法主要有增加桩长、桩径、桩数、桩后土体改良等措施。然而,桩基础的水平承载性能与桩长、桩径、桩后土体加固等因素呈非线性关系。由于承受较大水平力的特殊情况的需求日益加剧,对桩基础的水平承载能力提出更高的要求。地下连续墙因其整体刚度大、水平承载力高,有效解决了软土地区深基坑工程支护问题[7],广泛应用于桥梁锚碇基础与超高层建筑基础中。值得注意的是,地下连续墙基础最显著的不足就是经济成本过高。

伴随地下连续墙技术的不断发展,日本把桩基和地下连续墙结合起来,尝试在地下连续墙施工时在其内部放入现浇灌注桩或预制桩,从而构建地下连续墙与桩基协同工作的模式,二者共同承担上部荷载,成为承载力和刚度更优的基础形式[8]。鉴于承受水平荷载的基础结构的受力特性多表现为中上部弯矩和变形大、下部弯矩和变形小的特点[9-11],魏焕卫等[12]首次提出将群桩和地下连续墙结合,采用“上部墙体+下部群桩”,二者通过钢筋锚固连接的方式建立组合基础。区别于复合基础,该形式可以充分发挥地下连续墙刚度大、下部桩基基础嵌固的优势,符合变形大的位置增加刚度限制变形量、变形小的区域减小刚度控制经济成本的变刚度设计新理念。

目前,针对桩基和地下连续墙的水平承载特性的分析,国内外学者进行了大量的相关试验[13-17]及数值分析[18-19]研究。Ashour等[20]研究了湿陷土中的轴向加载桩行为,利用不同初始条件的湿陷性土壤样本建立土壤应力-应变关系相关性,将其集成到桩土模型中,以预测桩的轴向响应。Küçükarslan等[21]采用边界元和有限元相结合的方法对水平受荷桩基进行了相应的分析。戴国亮等[22]采用水平载荷试验分析了井筒式地下连续墙-土芯-外部土体的相互作用机理。罗鑫[23]分别通过室内模型试验和数值模拟研究了变截面井筒式地下连续墙的水平承载特性,并提出了适用于变截面井筒式地下连续墙的理论计算方法。然而,由于地下连续墙-桩组合基础是依托于地下连续墙和群桩发展改进的一种新型基础形式,目前对于地下连续墙-桩组合基础的承载特性研究较少,大部分成果均是针对群桩基础和地下连续墙单一的基础形式。

为了探究新型地下连续墙-桩组合基础的水平承载特性,明晰新型基础周围土体的水平变形性状、内力变化规律及荷载分担比是亟须解决的关键问题所在。因此现通过开展现场试验,并与数值模拟相结合,对地下连续墙-桩组合基础的水平承载特性及其受力性状进行研究,以期为今后的设计和施工提供指导。

1 现场试验概况

1.1 工程地质条件

试验场地位于山东省济南市平阴县黄河沿线高速公路工程场地内,试验场地为黄河三角洲第四纪冲积平原地貌,场地内主要分布粉土层和粉质黏土层,该场地地下水位位于-1.0 m左右。场地土层从上到下的分布情况如表1所示,并给出了土层物理力学性质参数指标。

表1 土层物理力学参数Table 1 The mechanical parameters of the soils

1.2 现场试验方案

结合场地条件,将现场试验设置为2组(T1和T2),共4个模型,每组两个基础模型(C1和C2)之间架设千斤顶,互为反力装置,如图1所示。桩基础采用钢管代替钢筋笼来制作灌注桩,具体施工为先钻孔→下放钢管→浇筑混凝土。钢管内径146 mm、壁厚6 mm,浇筑完毕后的桩径220 mm,桩长6 m。地下连续墙高1 300 mm,外墙尺寸为1 300 mm×1 500 mm,墙厚320 mm。为了保证组合基础的整体刚性,将钢管桩嵌入连续墙100 mm(图2)。

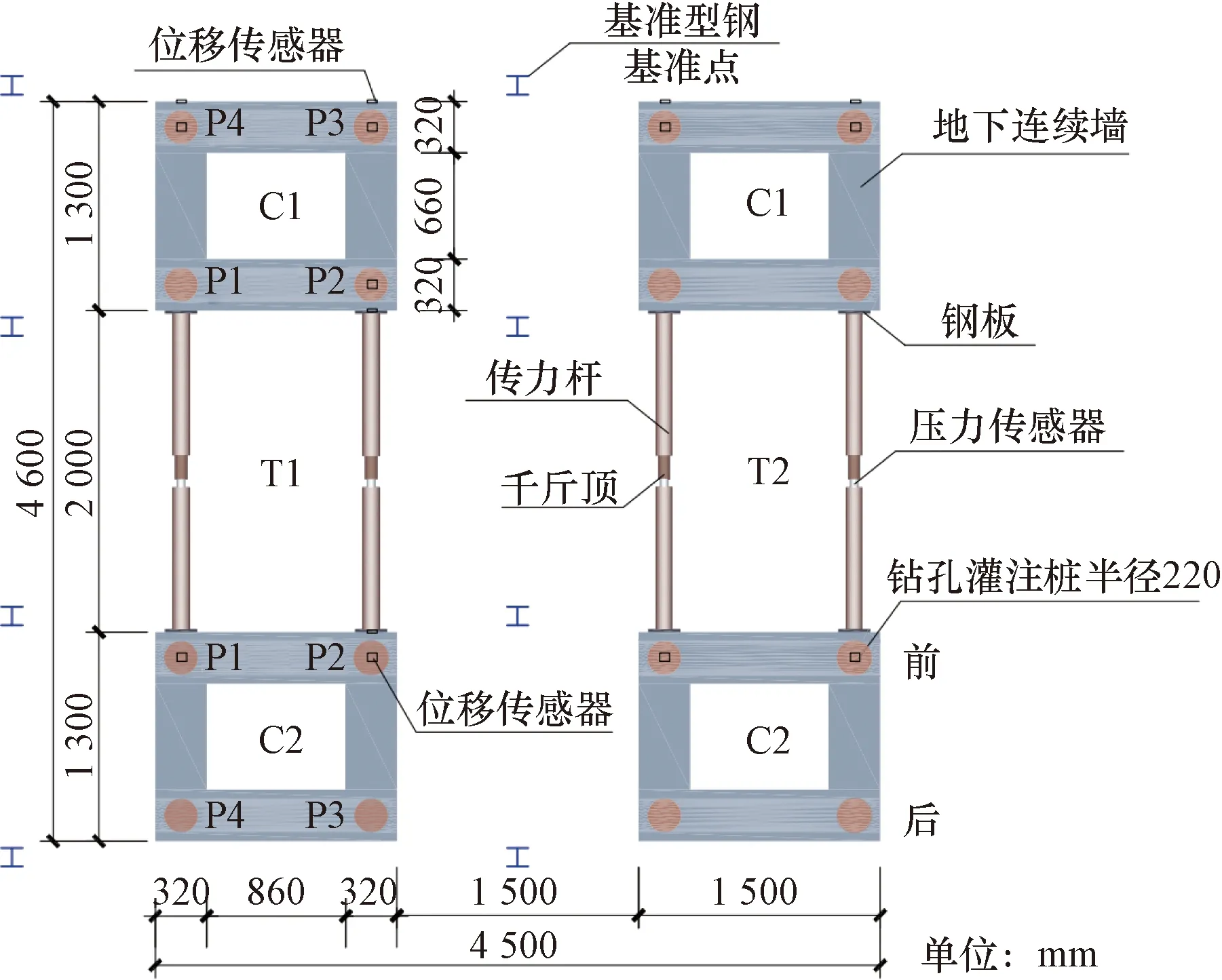
图1 现场试验平面布置图Fig.1 Layout of field test model

1.2.1 位移测量

位移传感器的布置如图1所示,组合基础的位移量测使用量程为50 mm与100 mm的电子位移计,通过磁性表座将其固定于基准梁上。在对应基桩位置的地下连续墙上部安置4个位移计,同时,在顺加载方向的前、后墙各安置两个位移计。

1.2.2 应变测量

应变采集选用1/4桥接线方式,其中,每组组合基础模型中应变片粘贴在P1(受荷处)与P4(背荷处)位置的钢管壁外侧(双面粘贴)和地下连续墙中对应P1、P4位置中心的纵筋外侧(单面粘贴)。连续墙自纵筋弯起位置280 mm处粘贴应变片,并每隔200 mm贴一个应变片,共5个。基桩自钢管顶部100 mm处开始贴应变片,并每隔200 mm贴一个,共6个;之后每隔400 mm贴一个,共10个。

1.2.3 土压力测量

土压力数据的量测,采用土压力盒进行采集。试验在地下连续墙后墙中线和P4处桩中心线位置的0.5、0.7、0.9、1.1 m位置处各安放一个土压力盒,收集该位置基础外侧土压力数据(图3)。

图3 土压力盒布置图Fig.3 Layout of the earth pressure cell

1.3 现场试验施工过程

处理后的钢管桩如图4(a)所示。桩基础施工过程中,为保证钢管位于桩孔的中心位置,在钢管的外侧焊接三组定位环,每组4个。桩基础的成孔方式采用水循环泥浆护壁的方法进行施工。

图4 组合基础的施工过程Fig.4 Construction process of the composite foundation

连续墙的制作分为4个部分,土体开挖、绑扎钢筋、支模和浇灌混凝土。开挖后将钢管桩露出坑底20 cm,然后在坑底浇灌10 cm厚垫层。待垫层强度达到要求后,对连续墙进行钢筋绑扎[图4(b)]。钢筋全部绑扎完成后,放置连续墙钢筋笼与外侧模板,随后进行连续墙的浇筑[图4(c)],最终现场试验加载状态如图4(d)所示。

试验采用两台50 t油压千斤顶同时进行水平加载(图5),为保证两台千斤顶同时提供相同的荷载,将两台千斤顶连接到同一台油压泵,进行数控加压。按照规范《建筑地基基础设计规范》(GB 50007—2011)[24],现场试验加载分5级进行,第一级加载值为200 kN,此后每级荷载增加100 kN。每级荷载施加后,在5、15、30、45、60 min时分别对组合基础顶部的水平位移进行读数记录,之后每隔30 min测读一次数据。

图5 卧式千斤顶Fig.5 Horizontal jack in test

2 数值分析

2.1 数值建模

组合基础数值模型与现场试验尺寸比例为1∶1,同时将数值模型边界设置为长10 m、宽10 m,总高度为9 m,以此减小边界效应的影响[25]。在模型构建过程中,用点线面的形式表示结构单元,通过对结构单元材料属性中的三维尺寸进行赋值定义来表示空间结构。地下连续墙采用板单元,桩基础采用“embedded桩”,具体材料参数如表2、表3所示。

表2 地下连续墙材料属性Table 2 The material properties of the diaphragm wall

表3 Embedded钢管桩材料属性Table 3 The material properties of embedded steel pipe piles

2.2 土体本构模型参数

土体本构模型选用土体硬化(hardening-soil,HS)模型,该模型可以较为准确地模拟土体从弹塑性到破坏阶段的应力、应变及刚度变化。根据现场地质资料,在桩身深度范围内土层多为粉土和粉质黏土,数值模型中将土体简化为两层土。

土体模型参数按照现场勘察报告以及当地经验值(E=3Es),所以上层粉土选取E50-ref=20 MPa,Eoed-ref=20 MPa,Eur-ref=3E50-ref=60 MPa。应力相关系数m按经验值取0.75,泊松比ν=0.3。具体参数如表4所示。

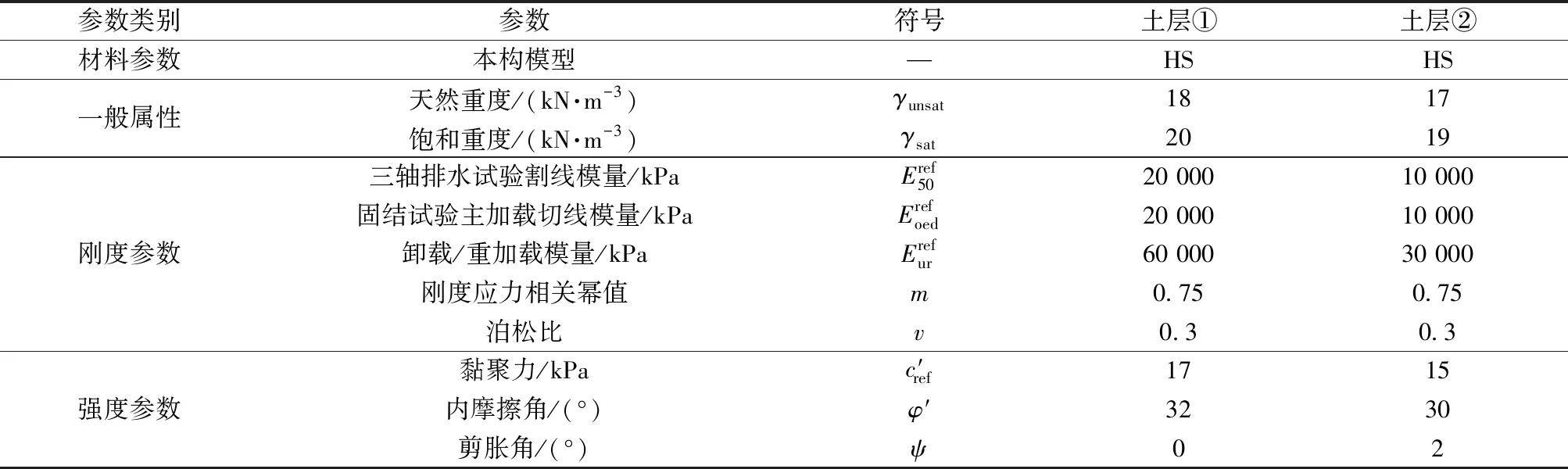
表4 基于现场试验的土体硬化模型参数Table 4 The parameters of the soil hardening model based on field tests

3 现场试验及数值结果分析

3.1 荷载-位移分析

现场试验中,通过布设在地连墙上部的位移传感器,测得基础顶部的水平位移和竖向位移。为使数据更具有规律性,对4组模型的位移结果取平均值,绘制出组合基础水平荷载-位移曲线,同时与数据模拟的荷载-位移曲线相对比。

3.1.1 水平位移

图6为不同荷载等级下组合基础顶部的水平位移变化规律。现场试验结果与数值模拟结果相近似,荷载达到400 kN之后,试验结果偏大,这主要是由于现场试验的影响因素众多,受现场环境影响较大。

图6 荷载-水平位移曲线Fig.6 Horizontal displacement results of the field test and numerical simulation

由图6可得,组合基础顶部的荷载和水平位移结果整体上呈非线性特征,并且具有显著拐点。在加载初期(<300 kN),水平位移曲线近似为线性,基础结构与周围土体的变形处于弹性变形阶段且位移较小,可以判定此时的荷载(300 kN)为临界荷载。随着持续加载,组合基础顶部的水平位移逐渐增大,变形处于弹塑性阶段。当加载到600 kN时,水平位移达到50 mm以上,这一阶段墙侧土体发生了塑性变形,达到组合基础承受的极限水平荷载。

3.1.2 竖向位移

现场试验测得了组合基础前墙和后墙顶部的竖向位移,并与数值模拟结果相对比,如图7、图8所示为组合基础在荷载为600 kN时的竖向位移云图。在荷载达到300 kN之前,两者结果相似,随后出现较大偏差,这是因为基础周围土体进入塑性变形阶段,较大的变形使得墙体产生了偏大的竖向位移。

图7 荷载-竖向位移曲线Fig.7 Vertical displacement results of the field test and numerical simulation

图8 组合基础竖向位移云图(600 kN)Fig.8 Vertical displacement nephogram of the composite foundation (600 kN)

在水平荷载作用下组合基础前墙的竖向位移,随着荷载的逐渐增加,由微小的向下的沉降逐渐转变为向上的隆起。这种现象是因为在施加水平荷载后,随着水平荷载的变大,模型在水平荷载与背荷面被动土压力的共同作用下会出现稍微倾斜的现象,由于倾斜的产生,作用在受荷面的水平荷载产生一个竖向分力和水平向分力,竖向分力和模型的自重带动基础产生向下的沉降,沉降达到一定程度,土体出现剪胀现象,产生一个回弹的趋势,之后水平向分力成为主导因素。

由现场试验结果,随荷载增加,后墙的竖向位移逐渐向下沉降,在400 kN时有一个回弹的趋势,在500 kN附近达到回弹最大值,然后继续向下沉降。产生这种现象是因为0～400 kN时组合基础整体绕某一点发生倾斜,400 kN之后出现向加载方向平移的现象,回弹现象是平移和倾斜二者共同作用的结果。从整体趋势来看,受荷面呈隆起趋势,背荷面呈沉降趋势,组合基础发生整体倾斜破坏。

3.2 桩墙弯矩分析

现场试验采集得到的应变值,需要进一步处理成弯矩值。根据式(1)求得弯矩。

M=εEW

(1)

式(1)中:ε为应变,采集数据得出的应变值为με,其关系为με=10-6;E为弹性模量;W为抗弯截面系数。

现场试验受周边环境、试验条件等因素的影响,试验数据存在偶然性,为了使实验数据更具有统计性和归纳性,首先对4组模型受荷面和背荷面桩墙在相同荷载下的弯矩取平均值。然后做出在不同荷载下4组组合基础桩墙平均弯矩-深度曲线,结果如图9、图10所示。

图9 受荷面弯矩-深度曲线Fig.9 Bending moment of the load-bearing surface

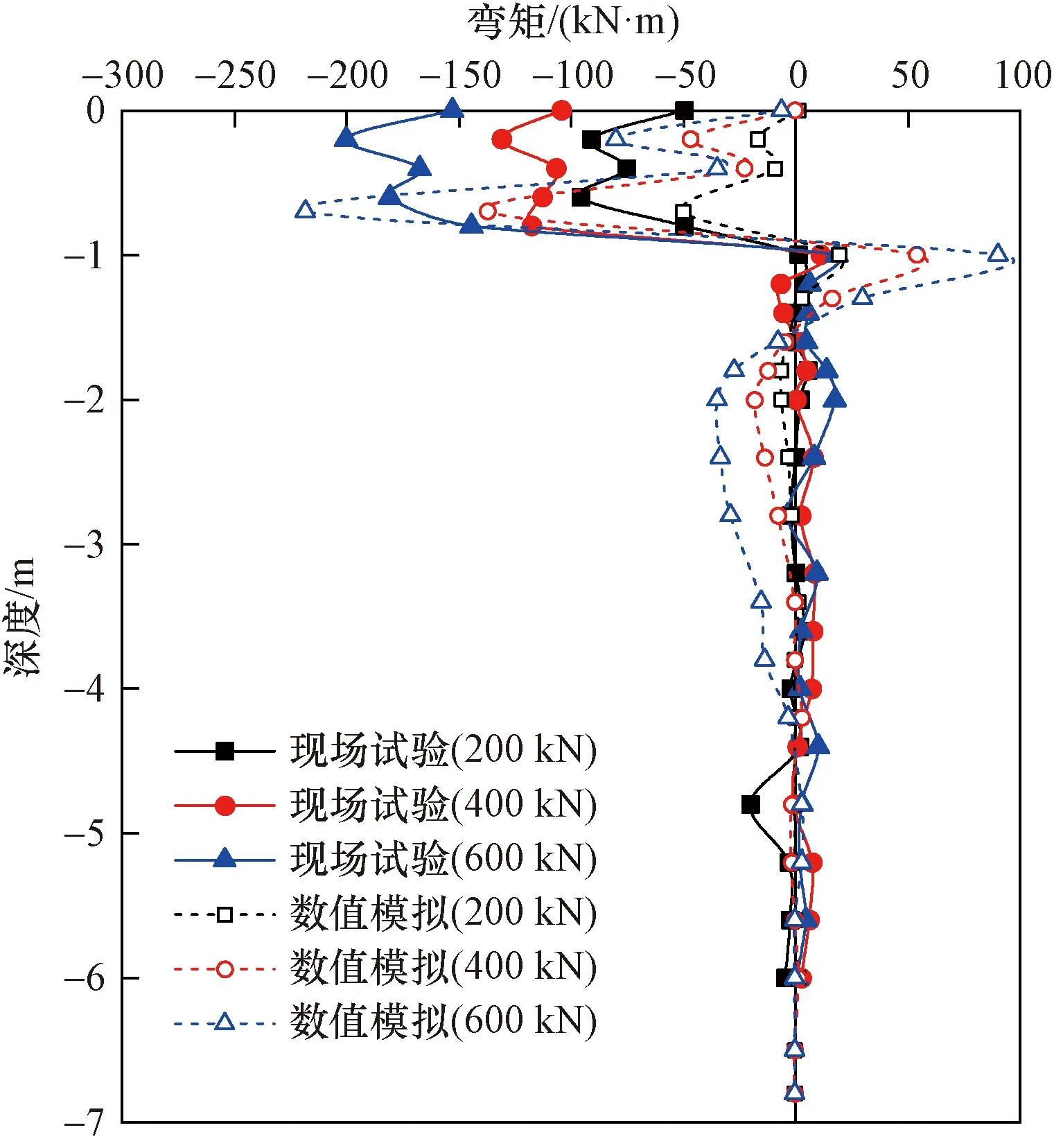
图10 背荷面弯矩-深度曲线Fig.10 Bending moment and depth curve of the loaded surface

从现场试验和数值模拟的弯矩变化趋势可以看出,弯矩沿深度方向呈非线性变化,在连续墙部分的趋势相似呈一个竖向放置的“M”形。弯矩沿深度先是增大,在墙1/5处达到第一个弯矩峰值。之后,弯矩开始减小,并且在墙的中部达到弯矩的一个极小值。随后弯矩继续增大,在墙4/5处达到第一个弯矩峰值,然后弯矩减小,在桩墙连接处附近达到弯矩反弯点。整体上看,受荷面弯矩承受的弯矩值为两倍的背荷面弯矩,这是由于水平荷载作用在组合基础前墙上部,随荷载的施加,组合基础发生水平位移,前墙承受主动土压力,而后墙承受被动土压力。现场试验与数值模拟的区别在于组合基础顶部的弯矩值相差较大,现场试验弯矩值远远大于数值模拟,这主要是由于现场试验荷载加载位置与地表存在一定的距离,而数值模拟中荷载较为理想的施加在地连墙上部。

通过弯矩分析与对比可知,无论是受荷面还是背荷面,弯矩都随着荷载的增加而增加,并且弯矩最大处的位置与弯矩峰值的位置不变。地下连续墙所受的弯矩远远大于桩所受到的弯矩。从埋深4.0 m处附近一直到桩底,弯矩几乎为0 kN·m,即桩的下半部分几乎不承受弯矩。受荷面和背荷面最大弯矩均出现在连续墙的中上部,说明此处为组合基础最薄弱的位置,在实际施工中钢筋设置应加密布置。

3.3 桩墙水平侧移

绘制桩墙身在各级荷载下水平变位,就必须先计算出各断面在各级荷载下的位移。现场试验中,根据位移传感器测得每级加载下的顶部位移,并结合桩身布置测点的应变片结果,由挠度方程[式(2)]计算式(3)和式(4),从而得到试验中组合基础各测点的转角和水平位移值[23]。数值模拟结果直接提取加载方向的水平位移值,对比如图11所示。

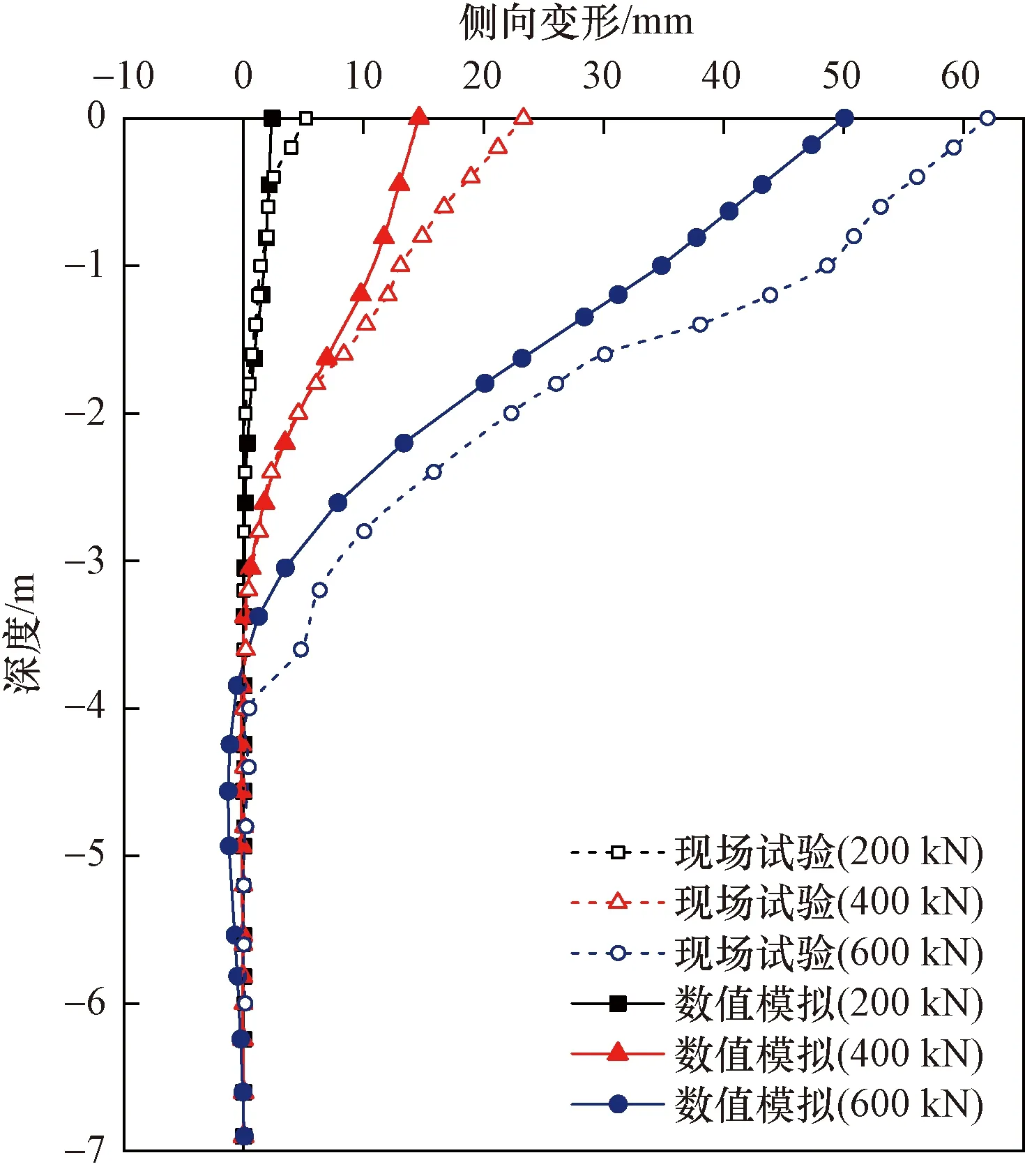
图11 桩墙身水平变位Y-Z曲线Fig.11 Horizontal deformation Y-Z curves of walls and piles

(2)

(3)

(4)

式中:Δεj、Δεj+1分别为j、j+1测点截面的应变;θj、θj+1分别为j、j+1测点截面的转角;yj、yj+1分别为j、j+1测点的水平位移;k0为j、j+1测点截面之间的间距;lj为j单元的长度。

通过现场试验推导得到的桩墙身水平位移值与数值模拟值相近,水平荷载下,桩墙身的水平位移随埋深逐渐减小。在第1～2级荷载作用下,组合基础的水平变形较小,不大于10.0 mm,随加载的进行,基础的水平变形逐渐显著,并且变形增量也开始增大。水平位移主要发生在组合基础上部的1/2段即地面以下0～3.0 m,其周边土体处于塑性变形,而桩身下部土体没有发生塑性变形。

此外,随着水平加载的进行,组合基础的第一位移零点及反位移沿埋深逐渐向下移动,由地下3.0 m左右发展到了地面以下3.85 m左右。水平加载的最后阶段反位移增大,处于-5.8～-4.0 m,其最后一级荷载出现的反位移最大值达到2.05 mm,位于地表以下4.67 m处。

3.4 桩墙组合基础水平承载力初步计算

地下连续墙-桩基础作为一种新型的组合基础,国内外对其研究较少,承载特性与设计问题仍需解决。根据组合基础的荷载传递特性及桩基承载力的计算,提出一种适合于桩墙组合基础水平承载力的计算方法。

根据桩基的计算,把基础看作是弹性体。根据《建筑桩基技术规范》(JGJ 94—2008)[26]可按式(5)估算桩身配筋率小于0.65%的灌注桩单桩水平承载力特征值,公式为

(5)

式(5)中:α为桩的水平变形系数;νM为桩身最大弯矩系数;W0为桩身换算截面受拉边缘的截面模量,m3;γm为桩截面模量塑性系数,圆形截面为2,矩形截面为1.75;ft为桩身混凝土抗拉强度设计值;An为桩身换算截面积,m2;ρg为桩身配筋率;Nk为在荷载效应标准组合下装顶竖向力,kN;ζN为桩顶竖向力影响系数,竖向压力取0.5,竖向拉力取1.0。

当桩的水平承载力由水平位移控制,桩身配筋率不小于0.65%时,可按式(6)估算,公式为

(6)

式(6)中:α为桩的水平变形系数;EI为桩身抗弯刚度,kN/m2;υx为桩顶水平位移系数;χ0a为桩顶允许水平位移,m。

丛蔼森[27]提出地下连续墙极限承载力的计算公式,公式为

PH=P1+P2+P3

(7)

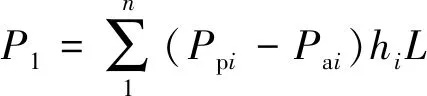
(8)

(9)

P3=N′btanθ+A′C′

(10)

式中:P1为基础前、后的极限水平承载力;P2为基础外侧面的极限水平承载力;P3为基础底面地基的极限水平承载力;Pai为基础背面的主动土压力;Ppi为基础前面的被动土压力;n为土层数;hi为地层厚;L为基础正面宽度;θ为土的内摩擦角;c为黏聚力;B为基础侧面宽度;fi为单位侧阻力;N′b为基础底面的地基黏聚力;A′为有效支撑面积。

由前文的分析可得,相比于传统的水平抗力基础,组合基础主要由地连墙和桩体上部来承担土体的水平压力,下部桩体主要起嵌固作用。地下连续墙-桩组合基础在水平荷载作用下受力如图12所示。

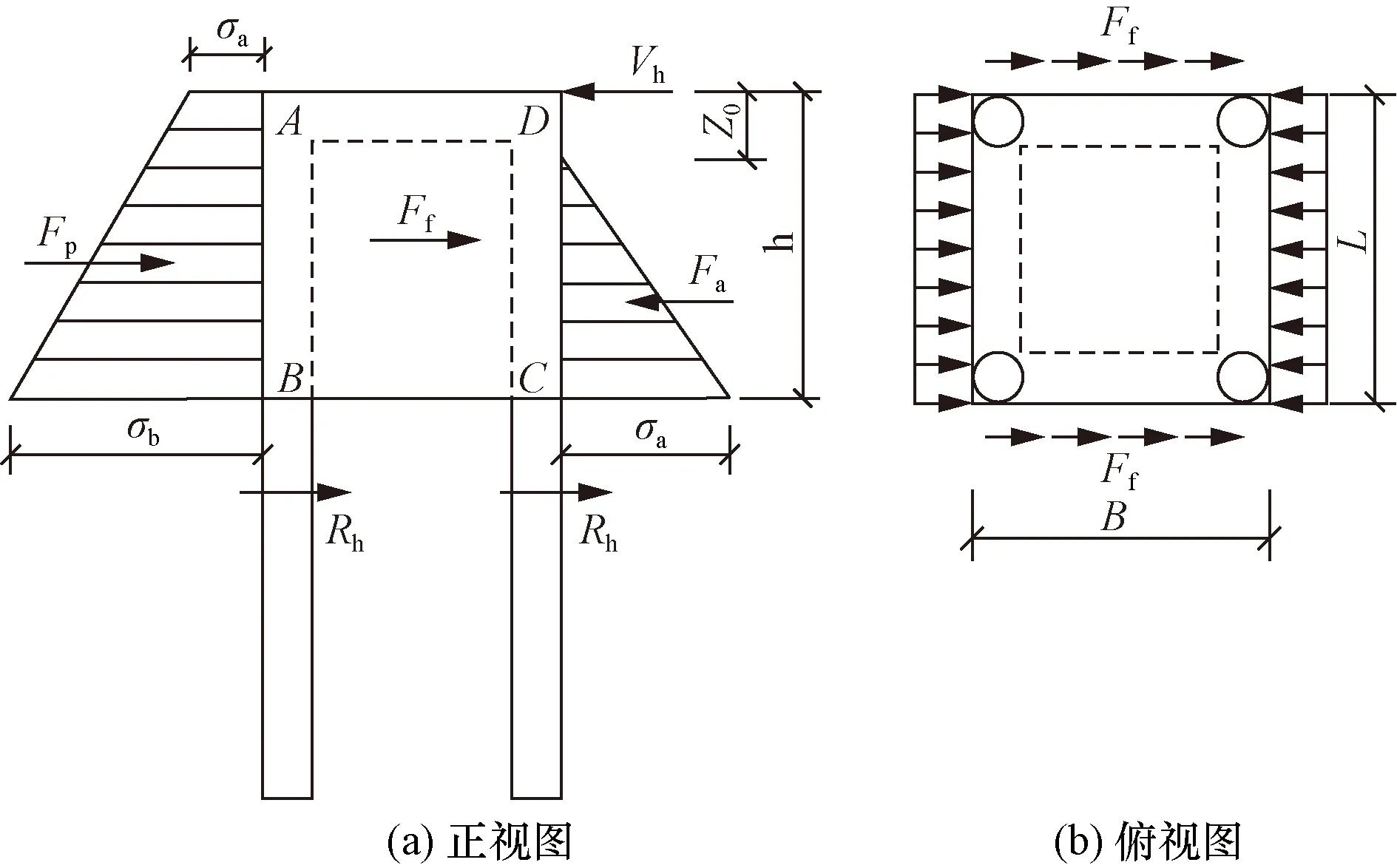
Fa为地连墙受荷面的主动土压力;Fp为地连墙背荷面的被动土压力;Ff为地连墙侧墙与土体的剪切摩擦力;Rh为地连墙底部与土体的摩擦力;σa为地连墙顶部位置处的侧向压力;σb为地连墙底部位置处的侧向压力;Z0为侧墙施加水平力情况下侧向土压力强度零点到地面的高度;地连墙的厚度;h为地连墙的高度;Vh为千斤顶施加的水平力图12 桩墙组合基础受力分析图Fig.12 The force analysis of the composite foundation

由以上分析可知,桩墙组合基础的水平极限承载力由上部地下连续墙基础的极限水平承载力PH和下部桩体极限水平承载力R组成,忽略墙内土芯对墙体的作用和群桩效应的影响,实际上两者并不能同时全部发挥作用。因此加入比例系数k1和k2,桩-墙组合基础水平承载力的计算可近似按式(11)计算,公式为

RH=k1PH+k2R

(11)

为初步确定比例系数k1和k2的取值范围,以数值模拟结果为参照,根据规范[26]确定水平位移为40 mm时对应的水平荷载为组合基础极限荷载,分别选取不同的k1和k2对现场试验结果进行计算。计算结果与数值结果对比如表5所示。

表5 现场试验近似计算结果与数值模拟结果对比Table 5 Comparison of approximate calculation results from field tests and numerical simulation

由表5可知,当k1=0.9,k2=1/2时,地下连续墙-桩组合基础水平承载力的近似计算结果与数值模拟结果相近。由于受试验次数、地质条件、基础尺寸等因素限制,此结果可为后续研究提供参考。

3.5 墙侧土压力分析

通过布设在后墙边侧和中间的土压力盒得到墙后土压力值。数据处理时将失效的测点值去除,再对剩余试验组取其平均值。数值模拟中找出与现场试验布设土压力盒相一致位置的土压力,绘制得图13、图14,同时相应位置的土压力云图如图15所示。

图13 中间土压力Fig.13 Earth pressure in the middle of the back wall

图14 边侧土压力Fig.14 Lateral earth pressure on the back wall

图15 数值模拟后墙的墙后土压力云图Fig.15 Earth pressure nephogram behind the back wall in numerical simulation

由土压力云图可以直观得出,墙后土压力随荷载的增加而明显增大,但从竖向上看,土压力沿墙身增长缓慢,且边侧土压力大于中间土压力。水平荷载作用下,组合基础后墙外侧横向土压力的分布呈现复杂的墙-土相互作用的过程,墙侧土体受到压缩,土压力呈现为被动土压力形式。由桩墙水平变位情况可见,水平荷载施加后,上部土体发生较大位移,被动土压力较大,下部土体位移较小,土压力增值较小。

3.6 墙侧地面的横向变形

根据数值模拟和现场试验讨论了组合基础的影响范围以及地面变形形式的演变。数值模拟中以水平荷载300 kN和600 kN为例,地面的横向位移分布如图16所示。

图16 组合基础周边地面横向位移分布图Fig.16 Lateral displacement diagram of the ground near the composite foundation

由土体位移云图可得,组合基础的沿加载方向的影响范围很大,桩内部土体整体性较高,位移较一致且数值较大。随着荷载的增加,组合基础的影响范围越来越大,从位移轮廓线来看,背荷面的影响范围远远大于受荷面的影响范围,加载方向(0.37B～1.95B)的影响范围明显大于正交于加载方向(0.1B～0.57B)的影响范围,其中,B为基础侧面宽度。

从现场各级荷载下墙侧土体的变形破坏情况来看,在加载初期,墙侧土体和墙后土体整体稳定性较好,未出现裂缝。随荷载增加,连续墙前墙外侧出现通长细微裂缝,同时在墙后侧的墙土交界位置附近出现沿加载方向细裂缝,连续墙两侧出现45°方向细长裂缝,墙前裂缝宽度持续增加。最后一级荷载施加后,组合基础周边土体加速失稳破坏,墙前水平裂缝宽度达4～5 cm,墙后土体土体隆起明显,两侧斜裂缝长度最长达到70 cm,宽4 cm。因此,在实际工程中可以通过改善组合基础主要影响范围内的土体性质提高承载力。