基于鲸鱼优化算法的变分模态分解和改进的自适应加权融合算法的管道泄漏检测与定位方法

2023-12-15易康蔡昌新廖锐全唐文涛

科学技术与工程 2023年33期

易康, 蔡昌新*, 廖锐全, 唐文涛

(1.长江大学电子信息学院, 荆州 434023; 2. 长江大学石油工程学院, 武汉 430100;3. 中国石油天然气集团公司气举试验基地多相流研究室, 武汉 430100;4. 油气钻采工程湖北省重点实验室, 武汉 430100; 5. 荆楚理工学院电子信息工程学院, 荆门 448000)

油气资源的主要运输方式是管道运输。相比于其他运输方式,管道运输具有安全、经济、高效的优势。在管道正常运营的过程中,因管道自然老化、各种输送介质的腐蚀、第三方活动以及自然灾害,时常发生管道泄漏事故。鉴于此,对输油管道进行实时泄漏监测与定位是保障管道安全运营、避免油气资源损耗的有效途径。目前常用的管道泄漏检测与定位方法主要有负压波检漏法[1-2]、声波法[3]、瞬态模型法[4]、漏磁内检法[5]、分布式光纤传感法[6]。其中负压波检漏法具有实时性高、技术成熟、检测成本低等优势,并广泛地应用到了管道泄漏监测领域中[7]。

负压波信号受外部环境的影响而包含噪声信号,如何滤除原始信号中的噪声分量对提高定位精度具有重要的实际意义。常用的信号降噪方法主要包括小波分析、经验模态分解(empirical mode decomposition, EMD)、集合经验模态分解(ensemble empirical mode decomposition, EEMD)以及变分模态分解(variational modal decomposition, VMD)[8]。小波分析表征局部信号的能力较强,但其降噪效果主要依靠小波母函数和阈值的选取,受主观因素影响较大。EMD是一种自适应信号处理方法,该方法根据信号本身的特征将其分解为一系列表征信号特征的固有模态分量(intrinsic mode function, IMF),但在信号分解的过程中容易出现模态混叠和端点效应现象[9]。EEMD在EMD的基础上,通过均方误差准则来区分高频信号和低频信号,但该方法存在分解耗时长和信号残留问题[10]。针对EMD及其改进算法的不足,Dragomiretskiy等[11]提出了一种完全非递归的VMD算法,该方法有效地避免了端点效应及主频部分的模态混叠问题,但该方法的模态层数和惩罚因子无法准确选取。

在管道泄漏检测领域中,对多传感器采集到的大量数据无法进行有效的处理也是影响定位精度的关键因素。因此,为了充分利用各传感器的实测数据,提高漏点的定位精度,需进行多传感器数据融合。张书奎等[12]采用贝叶斯推理法,但需要给出先验概率和错误决策代价。汪跃龙等[13]采用了最小二乘法,但该方法默认数据间的线性关系,受主观影响较大。Wu等[14]采用了自主学习能力强的反向传播(back propagation, BP)神经网络算法,但该算法的迭代次数多,难以得到理想的融合结果。

综上所述,现有的负压波检漏法存在定位精度低、易受噪声干扰、数据融合率低的问题,难以满足实际管道泄漏检测与定位需求。基于此,现提出基于鲸鱼优化算法(whale optimization algorithm, WOA)的变分模态分解(VMD)和改进的自适应加权融合算法(improved adaptive weighted fusion, IAWF)的管道泄漏与定位方法,与原有的双传感器负压波泄漏检测与定位模型对比,以期优化漏点的定位公式,而且避免负压波波速的干扰,减少定位计算的复杂度。针对传统VMD算法分解参数组合选取不当存在信号过分解和虚假分量问题,利用寻优能力强的鲸鱼优化算法(WOA)来搜寻VMD算法的最优分解参数组合,使其能输出最优模态层数和惩罚因子;针对原有数据融合算法存在冗余度高、计算量大的问题,提出改进的自适应加权融合算法(IAWF),先利用分布图法筛选出最优原始序列,再利用置信测度理论和自适应加权融合得到最优融合值,从而提升漏点的定位精度。

1 三传感器负压波泄漏检测定位原理

三传感器负压波泄漏检测定位模型如图1所示。设泄漏点在AB或BC段,Y1为压力变送器A、B之间的距离,Y2为压力变送器A、C之间的距离,X为漏点到压力变送器A的距离。ΔtAB表示压力变送器A、B检测到负压波信号的时间差,ΔtAC表示压力变送器A、C检测到负压波信号的时间差。负压波在输油管道中的传播速度为v,则存在下列关系式。

图1 基于三传感器负压波泄漏检测定位模型Fig.1 Leak detection and positioning model based on three sensors negative pressure wave

(1)

(2)

(3)

将式(1)～式(3)整理得

(4)

式(4)表明负压波波速不参与漏点定位公式的计算,漏点的定位精度取决于各压力变送器捕获负压波信号的时间差。在实际工况中,由于管道上的压力变送器所处位置不同,所接收到的负压波波速也不相同。设压力变送器A、B、C接收到的负压波波速分别为v、v(1+Δv1)、v(1+Δv2),则有如下关系式。

(5)

将式(5)整理得

(6)

对于钢质材料的管道,负压波的传播速度为1 000～1 200 m/s,则极限情况下Δv1和Δv2最大误差为20%,代入式(6)计算得X和X1之间的定位误差仅为0.8%,由此证明简化后的漏点定位公式具有准确性和有效性。

2 基于WOA-VMD的降噪算法

2.1 变分模态分解

变分模态分解的实质是将信号在变分约束框架下分解为若干个具有固定带宽和中心频率的固有模态函数,其中分量个数由预先设定的分解层数K决定。原始信号的分解过程即为变分问题的求解过程[15],VMD算法构建的约束变分模型为

(7)

式(7)中:f为原始信号;{uk}为经过VMD分解得到的各IMF分量;{ωk}为各IMF分量对应的中心频率;*表示卷积运算。

为求得变分模型的最优解,引入增广拉格朗日函数,故而将有约束变分问题转化为无约束变分问题,构造的增广拉格朗日函数表达式为

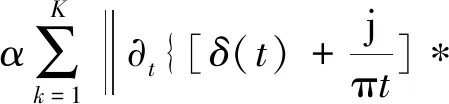
(8)

式(8)中:α为惩罚因子;λ为拉格朗日算子。

(9)

(10)

(11)

(12)

2.2 鲸鱼优化算法

鲸鱼优化算法[16]是于2016年由Mirjalili S和Lewis A提出的一种新型群体启发式的智能优化算法,通过模拟海洋生物中鲸鱼种群的狩猎过程来达到优化搜索的目的。对比粒子群算法(particle swarm optimization, PSO)、遗传算法(genetic algorithm, GA)等,WOA算法具有收敛速度快、优化精度高以及寻优能力强[17]等优势。WOA算法主要包括3个核心步骤:包围猎物、气泡攻击和搜寻猎物。

2.2.1 包围猎物

在WOA算法中,鲸鱼个体有能力包围和定位猎物,假设当前最优解或者近似最优解为目标猎物,则鲸鱼种群中的其他个体会向着当前离目标猎物位置最近的鲸鱼方向靠拢,并不断更新自身位置。更新位置的方式如下。

D=|CX*(t)-X(t)|

(13)

X(t+1)=X*(t)-AD

(14)

式中:t为当前迭代次数;X(t)为当前鲸鱼个体的位置向量;X(t+1)为更新后的鲸鱼位置向量;X*(t)为当前目标猎物的位置向量;D为每次包围时的步长;A和C为系数向量,其向量元素的计算表达式如下。

A=2ar1-a

(15)

C=2r2

(16)

(17)

式中:r1和r2为[0,1]的随机数;a为收敛因子,在迭代的过程中由2线性递减为0;tmax为最大迭代次数。

2.2.2 气泡攻击

在鲸鱼捕猎的过程中,鲸鱼个体有两种捕食行为,分别是收缩包围机制和螺旋更新位置。

(1) 收缩包围:当收敛因子不断更新时,鲸鱼个体的位置系数也随之发生变化,使得鲸鱼个体逐渐接近猎物的位置,最终完成对猎物的包围。

(2) 螺旋上升:当鲸鱼发现目标猎物时,首先计算当前各鲸鱼与猎物之间的距离,再通过螺旋上升的方式对猎物进行包围。该方式的数学模型表达式为

D*=X*(t)-X(t)

(18)

X(t+1)=eblcos(2πl)D*+X*(t)

(19)

式中:D*为当前鲸鱼个体与目标猎物之间的距离;b为对数螺线形状的常数;l为[-1,1]的随机数。

鲸鱼种群捕获目标猎物时,鲸鱼个体会随机选择收缩包围机制行为和螺旋上升更新的行为来包围猎物。为了更好地描述此行为,引入概率p作为选择阈值,p为0～1的随机数,概率阈值一般设置为0.5,该过程的数学模型表达式为

(20)

2.2.3 搜寻猎物

上述步骤均是鲸鱼种群在局部范围内寻找最优个体的位置。为了防止出现局部最优问题,提升WOA算法的全局寻优能力,设定系数向量|A|≥1,迫使鲸鱼远离目标猎物,让其在全局的范围内随机地搜寻鲸鱼个体来更新自身的位置。该过程的数学模型表达式为

D=|CXrand(t)-X(t)|

(21)

X(t+1)=Xrand(t)-AD

(22)

式中:Xrand(t)为种群中随机选择的鲸鱼位置向量。

2.3 WOA优化VMD参数

2.3.1 样本熵值

利用鲸鱼优化算法寻找最优参数组合的核心步骤是如何构造最佳适应度函数。样本熵值(sample entropy, SE)是用来度量时间序列混乱度的指标[18],样本熵值越小,表明序列中包含的有效信息越多,进一步说明分解后的序列越平稳,分解效果相对更好。相比于其他信息熵值,样本熵值仍然能提取出低信噪比信号中的噪声分量,抗干扰能力更强。基于此,通过样本熵值来构造WOA-VMD优化算法的适应度函数。

2.3.2 WOA-VMD寻优流程

基于上述分析,WOA算法优化VMD参数的流程如图2所示。具体实现步骤如下。

图2 WOA算法优化VMD参数流程图Fig.2 Flow chart of the WOA algorithm for optimization VMD parameters

步骤1初始化WOA算法的种群数量、最大迭

代次数、空间维度以及鲸鱼初始位置,并设置VMD算法中的分解层数K和惩罚因子α的取值范围。

步骤2对原始信号进行VMD分解,得到各IMF分量,并计算各IMF分量的样本熵值,选取其中样本熵值最小的分量作为全局搜索的适应度函数。

步骤3在区间[0,1]内随机生成概率p,若p≥0.5,则以螺旋上升的方式更新鲸鱼位置;若p<0.5且|A|≥1,则以随机搜索方式更新鲸鱼的位置;若p<0.5且|A|<1,则以收缩包围方式更新鲸鱼位置,并且保存当前的最优适应度函数。

步骤4将上一轮迭代更新后的鲸鱼种群位置作为下一轮的初始种群的位置,并重复步骤2～步骤4,直到满足迭代条件为止。

步骤5当循环迭代结束时,输出最优适应度函数和最优参数组合[K,α]。

2.4 算法验证

为了验证基于WOA-VMD降噪算法的有效性,对管道泄漏产生的负压波信号进行降噪分析。设置WOA算法初始种群数量为10、空间维度为2、最大迭代次数为20、分解层数取值范围为[3,7]、惩罚因子的取值范围为[100,2 000]。图3(a)和图3(b)分别为适应度函数变化曲线和惩罚因子变化曲线。

图3 WOA-VMD算法寻优过程图Fig.3 WOA-VMD algorithm optimization process diagram

由图3可知,在寻优过程中,样本熵值随迭代次数增加而减小,并且最小样本熵值出现在第10代,之后最佳适应度函数值和惩罚因子均保持不变。当循环迭代结束时,输出的最优参数组合为[6,1 942]。根据最优参数组合对原始信号进行VMD分解,得出6个IMF分量,其时域和频域波形如图4所示,各IMF分量的样本熵值见表1。

表1 各IMF分量样本熵值表Table 1 Entropy table of each IMF component sample

图4 基于WOA-VMD分解后IMF分量的时频域波形图Fig.4 Time-frequency domain waveform of IMF component based on WOA-VMD decomposition

由图4(b)可知,经过WOA-VMD降噪算法分解后,各分量信号分布在不同频率段内,这有效地避免了不同分量之间的干扰。由表1可知,IMF1的样本熵值最小,并且比其他分量的样本熵值低一个数量级,这说明其所含噪声信号的成分也较少。为了更有效地区分噪声分量和信号主导分量,需要计算各IMF分量与原始信号的互相关系数。互相关函数反映的是IMF分量与原始信号的相关程度,其作用是找出噪声分量和信号主导分量的临界点。互相关系数的计算公式为

(23)

表2 各IMF分量与原始信号的互相关系数Table 2 Cross-correlation coefficient of each IMF component and original signal

根据互相关理论,互相关系数的绝对值小于0.19和大于0.9分别为极低相关性和极高相关性,介于0.20～0.39为低度相关性、介于0.40～0.69为中度相关性、介于0.70～0.89为高度相关性。设置互相关系数的筛选阈值为0.7,根据互相关系数和样本熵值筛选出噪声分量和信号主导分量。经过筛选,IMF2～IMF6为噪声分量,IMF1为信号主导分量,再对信号主导分量重构即可得到降噪后的信号。原始信号与经WOA-VMD降噪算法处理后的纯净信号如图5所示。

图5 负压波原始信号与降噪处理后的纯净信号对比图Fig.5 Comparison between the original signal of negative pressure wave and the pure signal after noise reduction

图5表明,在负压波传播过程中,受外部环境干扰所产生的高频噪声信号经过WOA-VMD算法降噪后波谷趋于平滑,并且完整地保留了原始信号的波形特征。综上分析,充分证明了所提出的基于WOA-VMD降噪方法的有效性和高效性。

3 信号奇异性检测

管道在运输的过程中,需要通过加温加压来保证管道内部介质的流动性,因此当管道发生泄漏时,会导致所采集的负压波信号发生突变。信号发生突变的时刻称为信号的奇异点,其含义是指信号本身有不连续点或其导数有不连续点。

信号奇异性检测的方法有多种,其中小波变换在时频域上均能反映信号的局部特征,可以准确地检测出信号突变点的位置。为了获得理想的检测效果,采用连续小波分析对降噪后的信号进行奇异性检测。

连续小波变换的卷积表达形式为

Wf(a,τ)=〈f(t),φa,τ(t)〉

(24)

式(24)中:φ(t)为小波母函数;a为伸缩因子;τ为平移因子;变换结果Wf(a,τ)称为小波变换系数。

设θ(t)是具有低通特性的光滑函数,将其一阶导数φ′(t)=dθ(t)/dt作为小波函数,式(24)可整理为

(25)

式(25)表明,在一定的尺度下,Wf(a,τ)与f(t)*θ(t)成正比例关系,则表示Wf(a,τ)的极大值点对应f(t)*θ(t)的突变点,即信号突变点转化为求小波变换的极大值点。通过对某一降噪后的负压波信号运用频域峭度(frequency domain kurtosis, FK)型小波函数进行奇异性检测,其结果如图6所示。

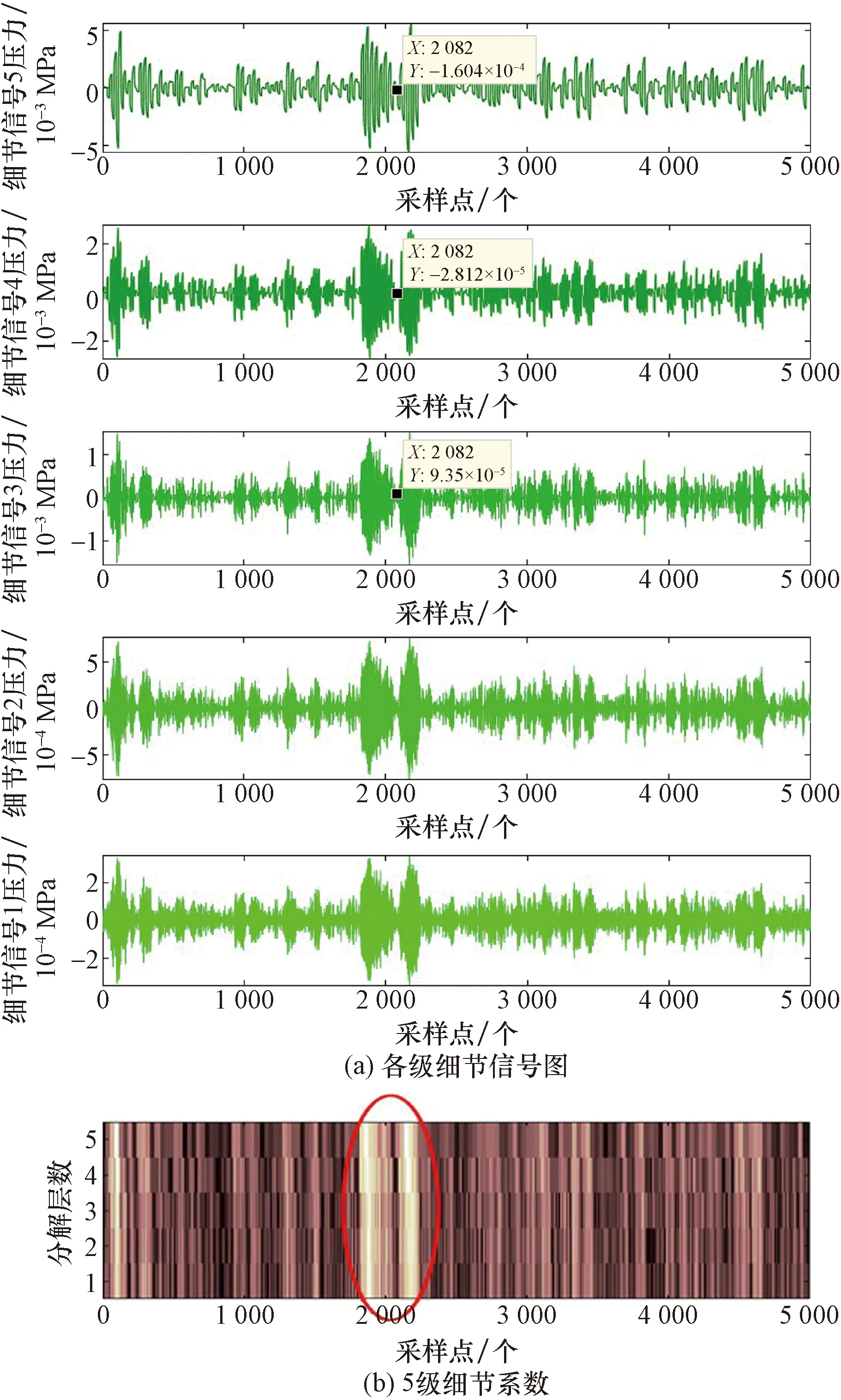
图6 某降噪信号FK型小波分析各细节信号图Fig.6 Detailed signal diagram of FK wavelet analysis of a noise reduction signal

由图6(a)可知,各细节信号的波形具有较强的对称性,从后三层细节信号图中可以准确得出信号突变的时刻。由图6(b)可知,亮斑条纹颜色越深,表明在该点处的细节系数也越大,信号的奇异性特征也越明显。

4 改进的自适应加权融合算法

4.1 数据预处理

在采集数据过程中,压力传感器受外界环境和自身因素的影响,使得测量值与真实值之间存在较大的误差,这种误差称为疏失误差。含有疏失误差数据会对定位精度造成较大的影响,因此需要利用数学方法予以剔除。判断疏失误差的主要方法包括拉依达准则、格拉布斯准则、分布图法[19]。拉依达准则适用于测量次数趋于无限大的情况,而当测量次数有限时,该准则是无效的。格拉布斯准则适用于服从正态分布的数据,而实际管道泄漏检测中的数据一般是非正态的。分布图法对多样本数据和非正态的数据均适用,是处理含有疏失误差数据的理想方法。

设传感器在不同时刻测得n组数据,并且各组数据之间相互独立。将n组数据从小到大排列,得到原始序列(Y1,Y2,…,Yn),则该序列的中位数为

(26)

将求得的中位数Ym与原始序列中最后一个元素Yn构成上五分位区间[Ym,Yn],与第一个元素Y1构成下五分位数区间[Y1,Ym]。进一步可求得上五分位区间的中位数为PU,下五分区间的中位数为PL,则五分位的离散度为

dp=PU-PL

(27)

设定一个判断标准θ,当原始序列中的元素与中位数差的绝对值大于θdp时,则将该元素视为无效数据。即原始序列中有效数据的判定区间为[d1,d2],表达式分别为

(28)

θ取值一般为[0.5,2.0],其大小一般取决于系统的测量精度。通过上述步骤,即可剔除原始序列中含疏失误差的数据,从而得到最优数据序列。

4.2 置信距离矩阵

设xi、xj分别为第i组和第j组数据的观测值,若xi、xj的数值相差较大,则说明两组数据的观测值相互支持度低,反之则说明相互支持度高。观测值之间的支持程度称为相关支持度,为了直观反映xi和xj之间的相关支持度,引入置信距离测度[20],计算公式为

(29)

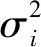
设定一个判断标准值ξ,当两组传感器之间的置信距离测度小于或等于ξ时,表明两组实测数据相互支持,反之表明两组数据不相互支持。则有如下关系式。

(30)

进一步得出置信距离矩阵为

(31)

由置信距离矩阵知,第i列所有元素之和为第i组数据的相关支持度。因此可以从置信距离矩阵中找出相关支持度最高的实测数据,用该组实测数据代替异常数据。

4.3 最优加权因子

(32)

总均方差为

(33)

因为原始序列中的元素相互独立且为x的无偏估计,故E[(x-xi)(x-xj)]=0,则σ2可改写为

(34)

从式(34)可知,总均方误差是加权因子的多元二次函数,则根据相应的高等数学知识可求得最优加权因子为

(35)

此时对应的最小均方误差为

(36)

5 管道泄漏检测与定位流程

管道泄漏检测与定位流程如图7所示。由于外部环境的干扰,所采集的负压波信号往往伴随着高频噪声信号,而噪声信号会对定位精度产生较大的影响,因此首先需要采用WOA-VMD降噪算法对采集的负压波信号进行降噪处理。在此基础上,对降噪后的负压波信号运用FK型小波函数进行奇异性检测,从而计算出压力变送器捕获负压波信号的时间差序列。紧接着采用分布图法对原始数据序列进

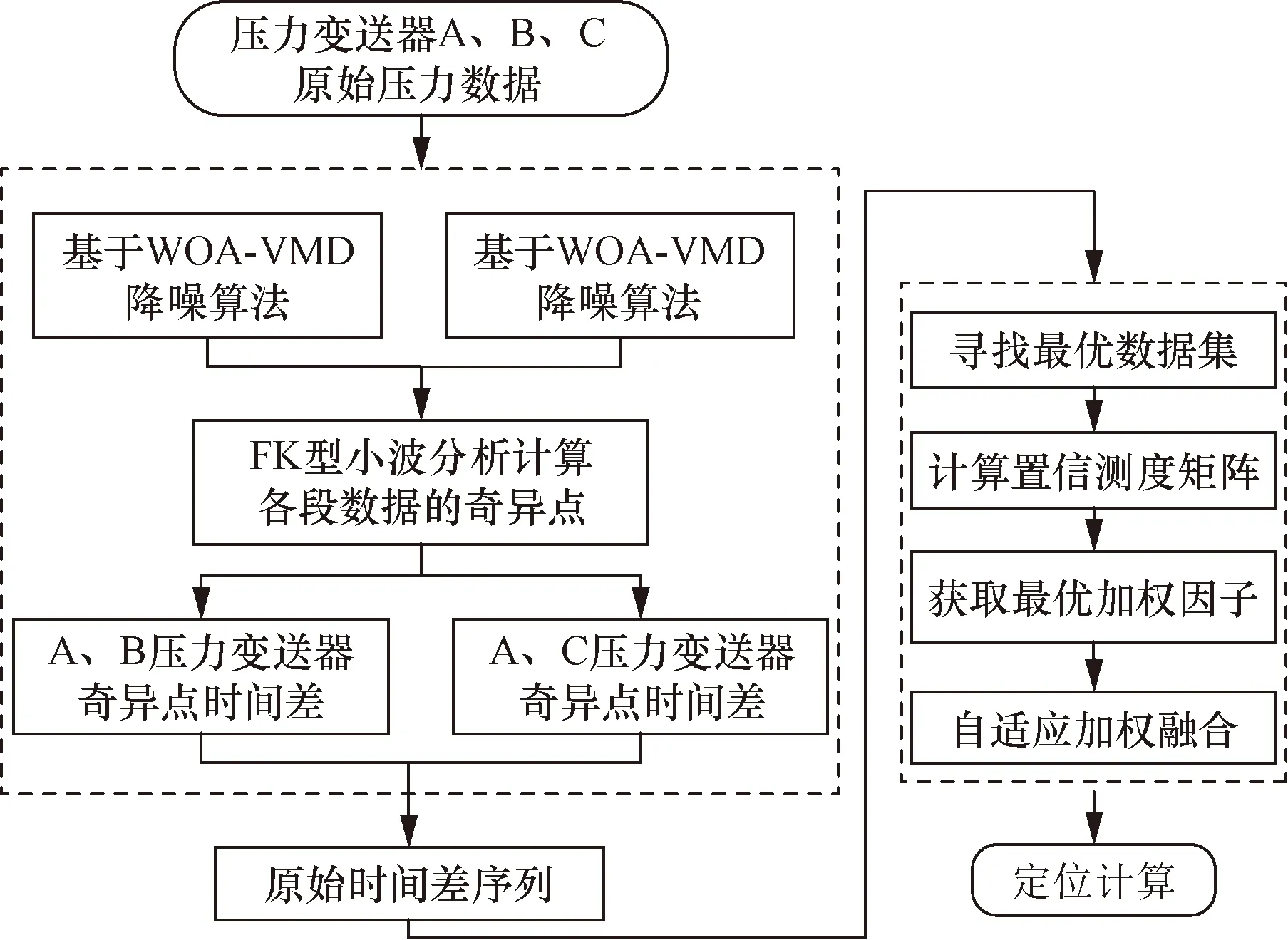
图7 基于WOA-VMD和IAWF的管道泄漏定位流程图Fig.7 Flow chart of pipeline leakage location based on WOA-VMD and IAWF

行预处理,得到最优数据集;再根据置信测度理论对异常数据进行替换,减少实测数据的丢失;再进一步结合传感器的自身方差得出最优加权因子,并进行自适应加权融合,得到最优融合值。最后,将经过上述步骤得到的最优时间差参数代入定位公式进行漏点的定位计算。

6 实验验证

为了验证所提出的管道泄漏检测与定位方法的有效性,在长江大学多相流重点实验室搭建管道泄漏检测实验平台进行实验。实验平台示意图如图8所示,管道的型号为304不锈钢管,采用环形方式沿实验室进行铺设,管道直径为30 mm,总长为160 m。在管道不同位置安装了3个压力传感器,其中压力传感器A与管道首端距离为10 m,压力传感器C与管道尾端距离为4 m;A、B压力传感器之间的距离为111 m;A、C压力传感器之间的距离为146 m。在管道上连接一个阀闸用来设置泄漏点,泄漏点与压力传感器A的距离为49 m。

图8 管道泄漏检测与定位实验平台示意图Fig.8 Schematic diagram of pipeline leakage detection and positioning experimental platform

数据采集卡与压力传感器相连,并将采集到压力数据保存到计算机中。实验过程中,在不同时间段内共进行了10组实验。首先对每组采集的压力数据进行降噪处理,再利用信号奇异性检测求出每组压力信号突变的时刻,进而求出不同压力传感器检测到负压波信号的时间差。预处理前的数据参数如表3所示。

表3 预处理前的数据参数表Table 3 Data parameters table before pretreatment

根据上述所提出的数据预处理方法,筛选出ΔtAB的最优序列为{x1,x2,x4,x7,x8,x10};ΔtAC的最优序列为{x3,x4,x6,x7,x8,x9}。设ΔtAB和ΔtAC对应的置信距离矩阵分别为R1、R2,通过计算ΔtAB和ΔtAC的置信距离矩阵来得出支持度最高的序列元组,R1和R2具体表示如下。

由R1可知,矩阵中第4列元素之和最大,相关支持度为6,对应到真实序列元组为第7组。由R2可知,矩阵中第4列元素之和最大,相关支持度为5,对应到真实序列元组为也第7组。因此用第7组数据代替原始序列中的异常元组,经过预处理后的数据参数如表4所示。同时为了直观地比较预处理前后的数据偏差情况,描绘了预处理前后的数据分布图,如图9和图10所示。再根据式(35)求得预处理后各组数据的最优加权因子,如表5所示。

表4 预处理后的数据参数表Table 4 Data parameters table after pretreatment

表5 各组数据的最优加权因子Table 5 Optimal weighting factors for each group of data

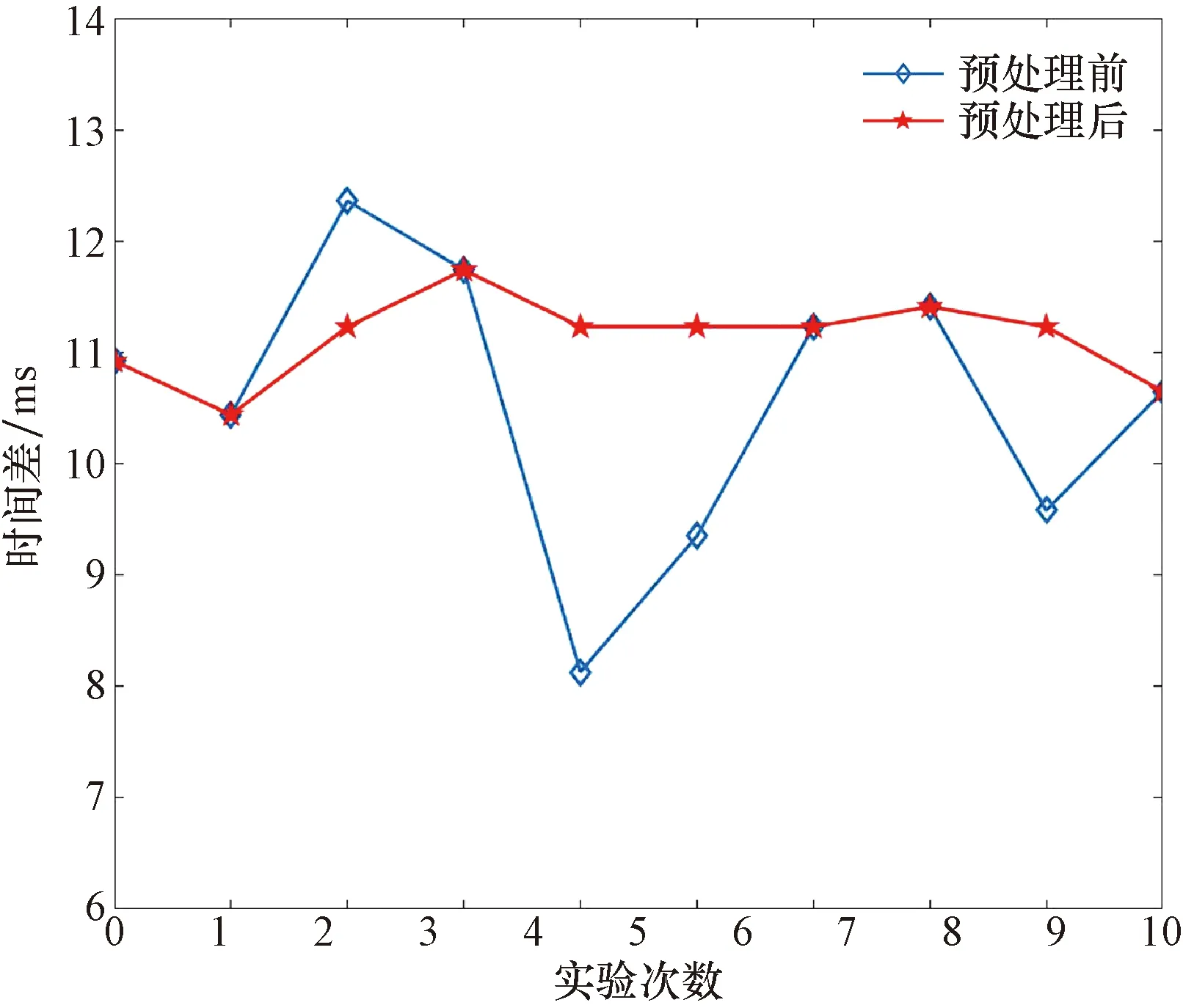
图9 ΔtAB预处理前后数据分布图Fig.9 Data distribution map before and after ΔtAB pretreatment

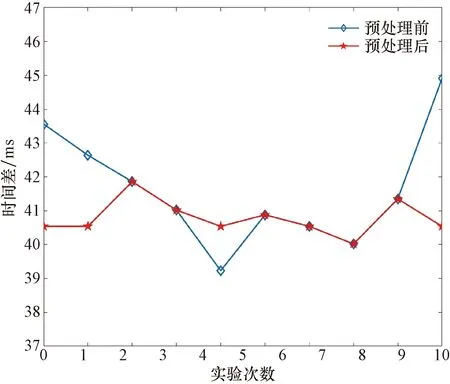
图10 ΔtAC预处理前后数据分布图Fig.10 Data distribution map before and after ΔtAC pretreatment

由图9、图10可知,经过IAWF算法预处理后的数据偏差变小。利用式(34)计算ΔtAB的最优融合参数为11.18 ms,ΔtAC的最优融合参数为40.59 ms,代入漏点定位公式得出定位结果为48.84 m。此外,采用算术平均法和传统自适应加权算法分别进行漏点的定位计算,算术平均法定位结果为49.53 m,传统自适应加权算法定位结果为49.56 m。3种定位算法的漏点定位结果如表6所示,可以看出,对比算术平均法和传统的自适应加权法,IAWF算法的定位结果更准确,相对定位误差可控制在1%以内。