稠油油藏化学降黏驱全耦合数值模拟方法
2023-12-15徐宏光束青林曹嫣镔于田田郑万刚冯海顺王玲
徐宏光, 束青林, 曹嫣镔, 于田田, 郑万刚, 冯海顺,3, 王玲
(1.中石化胜利油田分公司石油工程技术研究院, 东营 257000; 2. 胜利石油管理局博士后科研工作站, 东营 257000;3. 山东省稠油开采技术重点实验室, 东营 257067; 4. 中国石化胜利油田分公司, 东营 257001; 5. 南充职业技术学院, 南充 637000)
化学降黏驱是提高稠油油藏采收率的新方法[1-3]。胜利油田针对普通稠油油藏开展了降黏驱先导试验,取得较好的降水增油效果。降黏剂是化学降黏驱所采用的工作液,具有遇水增稠、乳化降黏、降低界面张力的作用[4-6],因此利用数值模拟软件对降黏驱替过程的表征和注采参数的优化具有重要的作用[7-8]。
一些学者利用数值模拟手段进行了化学驱的研究。孙致学等[9]对凝胶+降黏剂复合驱机理以及数值模拟实现方式进行研究,其利用化学反应将化学剂降黏的物化过程再现,但在物质平衡方面欠缺考虑。梁斌等[10]建立了三维非均质储层模型进行油藏数值模拟研究,重点分析了聚合物驱提高采收率机理。申乃敏等[11]利用Eclipse黑油模型进行了凝胶体系与聚合物注入参数优化研究,但研究中将凝胶采用高浓度聚驱代替,缺乏凝胶驱的数值模拟的模型和求解方法。胡渤等[12]在数值模拟中采用了流体黏度与化学剂质量分数关系曲线,建立了蒸汽吞吐后降黏化学驱模型,采用粒子群算法求解获得最优参数。李兆敏等[13]采用CMG软件进行了三维热化学驱的数值模拟,但并未阐述化学驱的数学模型。现有的数值模拟软件在传统的化学驱方面较为成熟,而对于化学降黏驱不能够很好地模拟。由于化学降黏过程引入的微观降黏机理[14-15]增加了数学模型的非线性程度,数模软件常采用等效替换或单向耦合的方式进行模拟。在处理雷诺输运方程时对浓度的散度采用一阶迎风格式,而一阶迎风格式在构造模式上有诸多不足,其对扩散项仍采用中心差分方法计算,夸大了扩散项的影响,所得解准确性没有中心差分格式高[16]。此外,由于数值模型求解方法选取不合适,造成数值模拟预测结果与实际值有较大偏差[17-18]。
因此,针对化学降黏剂驱,需要建立新的数学模型准确描述其控黏机理、驱油机理,合理解释化学降黏剂在室内和现场应用的驱替特征,优化降黏剂驱的注采参数。在物理模拟实验的基础上,现借助数值模拟方法建立封闭可解的浓度场-渗流场全耦合化学降黏驱数学模型,并对求解方法进行研究,深入认识降黏剂的驱油机理,提高稠油油藏降黏驱数值模拟准确性,为稠油油藏降黏驱开发方式优化与调整提供重要技术手段。
1 实验装置与方法
1.1 实验装置
实验装置由旋转黏度计、TX-500C全量程旋转滴界面张力仪、多功能驱替实验装置与三维物理模拟实验装置(图1)等组成。
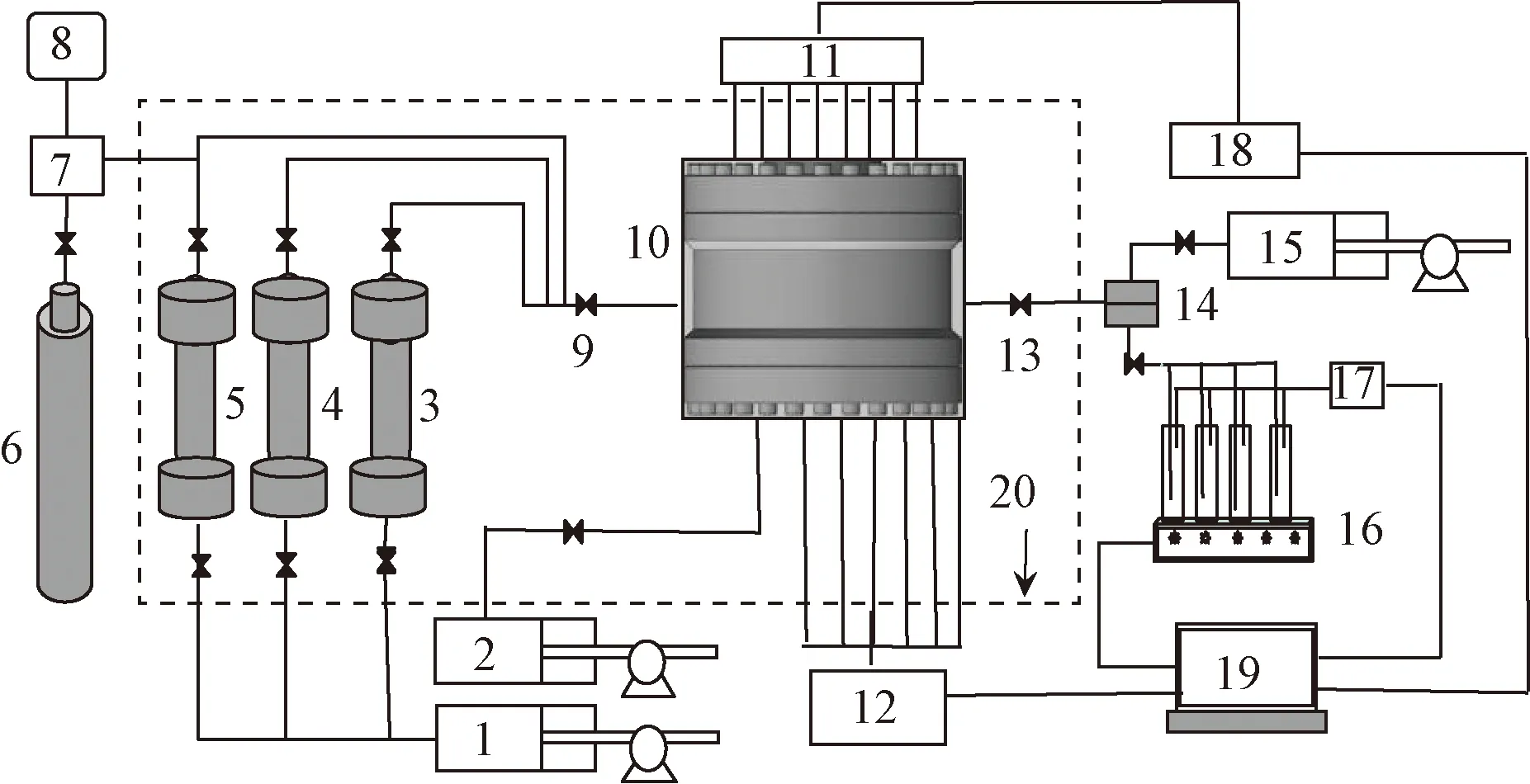
1为恒速恒压泵;2为围压泵;3为地层水中间容器;4为原油中间容器;5为气体中间容器;6为气瓶;7为增压泵;8为空气压缩机;9为进口端阀门;10为三维物模本体;11为饱和度测控装置;12为压力采集装置;13为出口端阀门;14为回压阀;15为回压泵;16为油水计量装置;17为质量流量计;18为采集箱;19为计算机;20为高温烘箱图1 三维物理模拟装置流程图Fig.1 Flow chart of 3D physical simulator
1.2 模型参数及实验材料
油样采用现场原油样品(黏度500 mPa·s)及稀释后的模拟油;实验用水采用地层水;相渗实验采用与储层物性相似的人造岩心,岩心渗透率为500 mD;三维物理模拟实验采用填砂岩心,为了与实际储层物性更加接近,模型平面内分为4个区域,纵向2层,上层1、2、3、4区渗透率分别为500、250、125、62.5 mD。下层1、2、3、4区渗透率分别为250、125、62.5、31.25 mD,油样采用模油(黏度50 mPa·s)。
1.3 实验步骤
乳液的黏度参照标准《稠油降黏剂通用技术条件》(Q/SH 1020 1519—2016)进行测定。
1.3.1 乳液黏度与含水率测试步骤
步骤1用地层水配制质量分数为0.3%的降黏剂溶液,将原油置于55 ℃恒温水浴1 h。
步骤2将油与降黏剂溶液按质量比为10∶0、9∶1、8∶2、7∶3、6∶4、5∶5、4∶6、3∶7、2∶8、1∶9依次加入比色管中,将比色管密封后置于55 ℃恒温水浴中。
步骤3保温10 h后,将样品取出,震荡观察乳化难易程度。
步骤4将发生乳化的溶液置于室温,观察乳液的脱水情况,直至水分完全脱出。
步骤5测量不同水油比乳化液黏度,绘制乳化液黏度-含水率曲线。
1.3.2 降黏剂溶液黏度-浓度测试步骤
步骤1用地层水配制不同浓度的降黏剂溶液。
步骤2将降黏剂溶液加入流变仪的外筒中。
步骤3将流变仪进行校正,外筒固定于流变仪上,放入与待样品相匹配的转子。
步骤4调整仪器温度,预热30 min后,测试降黏剂溶液的黏度。
步骤5更换不同浓度的降黏剂溶液,重复上述步骤。
1.3.3 相渗实验步骤
相渗实验依据标准《稠油油藏高温相对渗透率及驱油效率测定方法》(SY/T 6315—2017)进行。实验步骤如下。
步骤1岩心烘干称重,饱和地层水,计算饱和水质量。
步骤2将岩心装入夹持器内,为饱和油建立束缚水饱和度。
步骤3进行降黏剂溶液驱替,记录压差和产油量、产水量等实验数据。
步骤4更换岩样和不同浓度的降黏剂溶液,重复步骤1~步骤3。
1.3.4 三维物理模拟实验步骤
步骤1用气体检查三维物理模拟装置的密封性。
步骤2根据不同的沙粒配比填制非均质模型。
步骤3采用模拟地层水水驱至各生产井无气体后,记录注入和产出水量,计算模型的孔隙度。
步骤4以由低到高的注入速度进行油驱水饱和油,并老化120 h。
步骤5检测原始含油饱和度分布,各处含油饱和度分布满足精度要求,开始实验。
步骤6以设计注入速度注入设定浓度的降黏剂溶液,驱替至含水98%结束实验。连续采集压力、饱和度和产量等数据。
2 实验结果分析
2.1 模型参数获取实验结果
图2为乳化液黏度与含水率关系曲线,随着含水率的增加,乳化液的黏度降低,原油初始黏度为500 mPa·s,加入降黏剂溶液后,含水率在40%以前,乳化液黏度迅速降低,降幅达到90%,而后趋于平缓。通过拟合获得乳化液黏度-含水率关系,如式(1)所示。
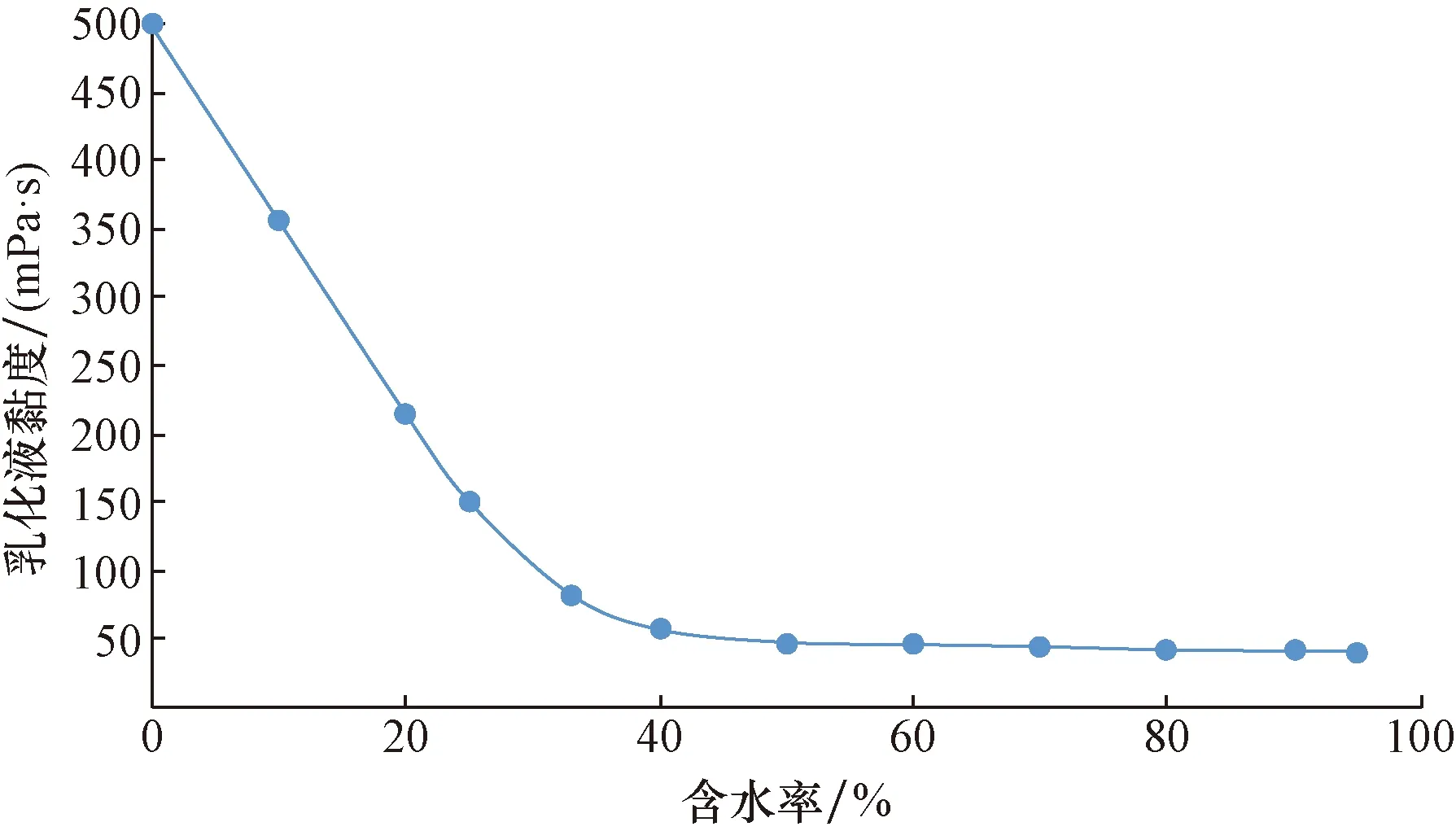
图2 乳化液黏度-含水率关系曲线Fig.2 Viscosity of emulsion versus water contain

(1)
式(1)中:μo为乳化液的黏度,mPa·s;Sw为含水率。
图3为降黏剂溶液黏度与浓度关系曲线,随着降黏剂溶液浓度的增加,降黏剂溶液黏度呈现线性增加趋势,拟合获得降黏剂黏度-浓度关系,如式(2)所示。

图3 降黏剂黏度-浓度关系曲线Fig.3 Viscosity-concentration relationship curve of viscosity-reducing agent
μw=0.073 6c-26.93
(2)
式(2)中:μw为降黏剂溶液的黏度,mPa·s;c为降黏剂溶液的浓度,mg/L。
图4为不同浓度降黏剂溶液与原油的界面张力,界面张力随着降黏剂溶液浓度的增加呈拟线性下降趋势,拟合获得降黏剂黏度-界面张力关系,如式(3)所示。

图4 不同浓度降黏剂溶液与原油的界面张力曲线Fig.4 Curve of interfacial tension between viscosity reducer solution and crude oil
σ=-0.021c′+0.825 7
(3)
式(3)中:σ为界面张力,mN/m;c′为降黏剂溶液的质量浓度。
该部分实验是为后续构建的数学模型求解提供补充方程。
2.2 相渗实验结果
为了获得数值模型计算所需的参数,进行了不同浓度降黏剂与稠油的相渗实验。图5为不同浓度降黏剂溶液与稠油的相渗曲线,可以看出,当降黏剂浓度由0.2%增大到1.0%时,油水两相流动是动态变化的,加入降黏剂后,油相渗透率升高,水相渗透率下降,等渗点右移且残余油饱和度减小。这是因为降黏剂溶液与原油接触能降低其黏度,且增大水溶液的黏度,从而改善了水油流度比,提高了波及系数和洗油效率,减小残余油饱和度。由于水溶液黏度的增大,引起水相渗透率减小,且降黏剂浓度越大,水溶液黏度也就越大,水相渗透率越小。当含水饱和度小于60%时,水相相对渗透率很低。降黏剂浓度从0.2%增加到1.0%,驱油效率提高了7.97%。

Kro为油相相对渗透率;Krw为水相相对渗透率图5 不同浓度降黏剂-油相对渗透率曲线Fig.5 Viscosity reducer of different concentrations-oil relative permeability curves
2.3 三维物理模拟实验结果
为了研究降黏剂驱的驱油规律,同时为三维数值模型修正和历史拟合提供必要的参数,开展三维物理模拟实验。图6为实验获得的非均模型不同孔隙体积(pore volume,PV)数下的饱和度分布图,可以看出初始含油饱和度分布较为均匀,0.5PV时水驱前缘接近突破,1PV时物性较好区域的驱替前缘突破,剩余油主要分布在生产井间位置以及物性差的区域。
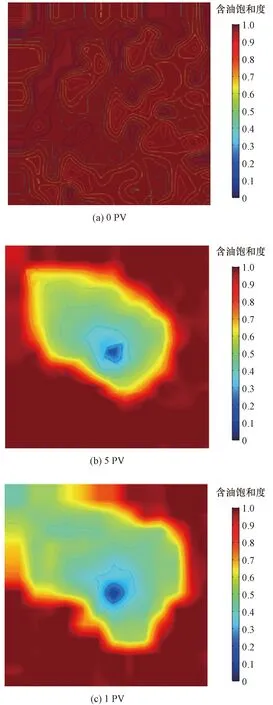
图6 不同PV数下饱和度分布图Fig.6 Saturation distribution under different PV numbers
3 化学降黏驱数学模型
由于岩心驱替实验难以反映水驱稠油油藏流场的演变规律,在物理模拟实验规律和机理认识的基础上,构建了浓度场-渗流场全耦合的降黏剂驱替数学模型,用于反演降黏驱的驱油规律,并进行注采参数的优化。
3.1 数学模型建立
全耦合化学降黏剂驱油模型是一种油、水两相流模型,乳化降黏剂在液相中的质量分数很小,认为是一种稀物质。假设化学降黏剂主要通过对流-扩散作用在液相中流动,且不考虑岩石、油水两相的压缩性以及温度对降黏剂性能影响。
对于水相可建立相应的质量守恒方程为

(4)
同理,对于油相可建立相应的质量守恒方程为

(5)
其中,对流速度服从达西定律,即

(6)
对于化学降黏剂的运动,使用雷诺输运方程描述为

(7)
饱和度约束方程为
Sw+So=1
(8)
毛管力方程为
pw-po=pc
(9)
(10)
式中:ρ为密度,kg/m3;v为达西速度,m/s;q为质量流量,kg/s;φ为孔隙度;S为饱和度;kr为相对渗透率;k为绝对渗透率,mD;p为压力,MPa;c为质量浓度,mg/L;D为扩散系数,m2/s;R为传质源汇项(可用于描述吸附沉降作用);σ为界面张力,mN/m。
模型由4个主要方程控制,渗流控制方程分别向传质方程和毛管力方程更新油水达西速度及饱和度数据,传质方程向流动控制方程更新降黏剂浓度从而更新油水黏度,而毛管力方程向流动控制方程更新毛管力进而更新相渗数据。其中,式(4)~式(9)包含So、Sw、vo、vw、μo、μw、pw、po、σ及c等10个未知变量,未知变量数目大于方程数目,方程组不封闭。为了实现上述模型求解,利用2.1节中获得的降黏剂溶液黏度-浓度关系等实验参数。
3.2 网格划分与模型求解
为对模型进行求解,对数值模型求解方法进行了研究,优先了有限体积方法。该方法兼顾了有限差分法的计算速度和有限元方法的计算精度,并且能够保证任一局部网格内流体质量守恒。因此研究中采用有限体积方法对数值模型进行求解。建立与实验岩心相同大小的圆柱形求解域,模型入口条件为速度边界耦合降黏剂浓度边界以模拟固定浓度降黏剂以固定速度流入;出口条件为压力边界,其值与大气压相同。圆柱外壁为无滑移边界条件,使用非结构四面体对求解区域进行网格划分(图7)。模型渗透率采用随机建模方法赋值,平均值为500 mD。

图7 数值岩心网格剖分结果Fig.7 The result of grid generation of numerical core
通过网格剖分可以获得一个相互不重叠且完全覆盖求解域的网格系统,首先在各网格内对前述方程组进行空间离散,由于流动控制方程与质量守恒方程均属于系数性偏微分方程,离散过程类似,此处仅以水相饱和度控制方程为例说明空间离散方法。首先对式(4)在网格Vc范围内进行积分,得

(11)
根据散度定理可将体积积分转化为面积分,将网格的面积分转化为网格各表面积分之和的形式,得
(12)
而其中面积分部分由梯形积分公式可转化为

(13)
由此可获得由流动控制方程[式(4)]的离散格式为

(14)
式中:λw为水相流体的流度,m2/(MPa·s);f~faces(Vc)为组成控制体Vc的界面;n为顶点;Sf为界面f上指向外侧的方向向量。
采用IMPES方法,首先求解每一个时间步上某一相的压力,然后求解该相的饱和度。假设当前时间步为k,则所有与压力相关的变量都采用k时间步的值进行隐式求解,而所有与饱和度相关的变量都采用k-1时间步的值进行显式求解。
3.3 线性模型模拟结果
图8为数值岩心饱和度及降黏剂浓度分布图,从油饱和度分布图[图8(a)]可以看出,越靠近入口端剩余油饱和度越低,驱替效果越好。尽管左侧为己驱替的区域,但剩余油饱和度介于0.1~0.4,仍有部分残余油无法采出。从降黏剂浓度分布图[图8(b)]可以看出,驱替前端降黏剂浓度较低,而越靠近入口端水溶性降黏剂浓度越高,这是由于扩散作用的存在导致降黏剂向前端的传播速度较慢,而降黏剂的浓度分布与水相黏度的分布保持一致。
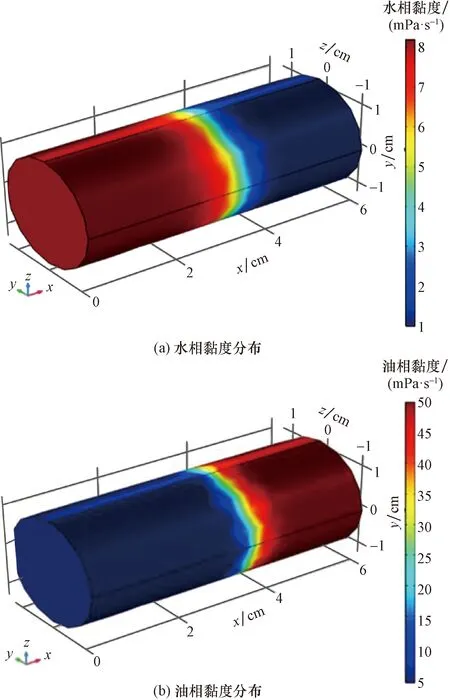
图8 数值岩心含油饱和度及降黏剂浓度分布图Fig.8 Oil saturation and viscosity reducer concentration distribution of numerical core
图9为数值模拟岩心中水相、油相的黏度分布图。由于降黏剂具有一定黏度,与降黏剂混合的水相黏度增高,水相黏度由1 mPa·s增加到8 mPa·s,而与降黏剂溶液混合的油黏度降低,油相黏度由初始时的50 mPa·s降低到5 mPa·s,油水黏度比由50 mPa·s降低到0.6 mPa·s,改善水油流度,扩大了波及体积,在驱替前缘形成“油墙”,实现油相的均匀驱替,从而提高采收率。
为了验证模型的可靠性,将数值岩心驱替结果与真实岩心实验结果对比,图10为两种岩心采出程度对比图。两种岩心采出程度吻合程度较好,显示在数值模拟中可以使用实验得到的降黏剂浓度和油水黏度的关系式表征降黏剂的驱替效果,建立的模型可以表征降黏剂的增黏和降黏效果。

图10 数值岩心与真实岩心的采出程度曲线Fig.10 Recovery of numerical and true cores
3.4 三维数值模型构建与模拟结果
3.4.1 三维数值模型构建
由于岩心级别的实验难以表征较大空间尺度下的驱油规律,因此,在物理模拟及线性模型模拟的基础上构建了三维大尺度数值模型。图11为三维数值模型示意图,模型尺寸为80 cm×80 cm×60 cm,布置反五点井网,通过属性分区将模拟区域划分为4×4个区域,对独立区域进行属性赋值模拟储层非均质性。采用Delaunay四面体对求解域进行网格剖分,求解域被划分为68 101个网格,相邻网格增长率1.45,曲率因子0.5。采用四面体体积与其外接球半径之比评价网格剖分质量,其中最小值0.65,平均值0.95,网格剖分结果满足仿真需求。模型孔隙度为30%,渗透率介于31~500 mD,相渗曲线采用时变相渗,黏-浓关系、乳化降黏关系采用前述实验结果插值,基质密度为2 300 kg/m3,降黏剂最大吸附量3 mg/kg,降黏剂吸附常数0.024 m3/mg,基质孔隙迂曲度为1.2,降黏剂扩散系数7×10-6m2/s。
图11 三维数值模型示意图Fig.11 Diagram of 3D numerical model
利用三维数值模型,通过调整相对渗透率曲线,对模型进行修正及历史拟合,拟合结果如图12所示。可以看出数值模型模拟结果能够很好地拟合物理模拟的结果,模型准确度较高,可以以此模型开展降黏剂驱油规律和注采参数优化研究。

图12 三维物理模拟实验与数值模拟结果图Fig.12 3D physical simulation versus numerical simulation results
3.4.2 三维模型模拟结果
图13为三维数值模型物性分布与不同PV数下含油饱和度分布图。随着降黏剂溶液的不断注入,近井带原油最先受效,原油黏度降低,在注入流体的驱动下向生产井流动。在降黏驱前期(0~0.5 PV),降黏剂流度改善作用下,驱替前缘形成“油墙”,此时产出液主要以纯油相形式产出,驱替后沿形成乳液,高渗层与低渗层产量比相似,高渗层的驱替前缘在0.5 PV时首先突破,低渗层的驱替前缘接近突破。随着驱替的进行(0.5~1 PV),在“油墙”结束后,后续注入降黏剂继续推动乳液流动,乳液渗流过程中的卡堵作用,促使低渗层与高渗层的原油进一步动用。后续水驱过程中,水相与油相流度比差,水相主要沿高渗通道窜流,采出油主要来源于高渗层。降黏驱后,平面上剩余油分布在采油井间区域, 纵向上低渗层位剩余油相对富集,后续水驱后,宏观上剩余油主要在井组边部区域以及低渗层位近井带富集。模型反演的驱油规律与物理模型实验结果相似,显示所建立的模型可以用于开展三维模型数值化实验研究。

图13 三维数值模型模拟结果图Fig.13 Simulation results of 3D numerical model
3.5 基于三维数值模型的注采参数优化
三维物理模拟实验存在难度大、周期长、可重复性差的问题,而建立的数值化实验方法较好地解决了上述问题。利用建立的三维数值模型开展降黏剂驱的数值化实验,研究了降黏剂注入浓度、注入量、注入速度及注入方式等参数对降黏剂溶液驱油效果的影响。
3.5.1 降黏剂注入浓度对采出程度的影响
模拟不同浓度的降黏剂注入驱油,研究注入浓度对采收率的影响。模拟采用连续注入的方式进行驱油实验,注入速度为15 mL/min,模拟时长固定为96 h。设计降黏剂溶液浓度分别为0、 0.2%、 0.4%、0.6%、0.8%进行驱替,对比模型的采出程度。图14为不同浓度降黏剂溶液与采出程度提高幅度关系曲线。随着降黏剂浓度的增大,相同时间内采出程度增大,且无水采油期延长。采出程度增长幅度随着降黏剂浓度增大呈现先增后减的趋势,合理注入浓度范围介于0.2%~0.5%,最优注入浓度为0.4%。

图14 不同浓度降黏剂与采出程度提高幅度曲线Fig.14 Increase of recovery degree versus viscosity-reducing agent with different concentration
3.5.2 降黏剂注入量对采出程度的影响
设计了连续水驱、0.2、0.4、0.6、0.8 PV的降黏剂溶液注入量,对比不同注入量下的采出程度。图15所示为不同注入量下的采出程度及剩余油饱和度图,随着注入量的增加,平均剩余油饱和度逐渐降低,采出程度逐渐增加,当注入量超过0.6 PV后,采出程度增幅趋于平缓,平均剩余油饱和度的降幅变缓,合理的注入量介于0.2~0.6 PV。

图15 不同注入量下的采出程度及剩余油饱和度图Fig.15 Recovery degree and remaining oil saturation at different injection rate
3.5.3 注入速度对采出程度的影响
设计注入速度分别为3、6、9、12、15、18 mL/min,对比模型的采出程度。图16所示为不同注入速度下采出程度变化曲线,采出程度受注入速度的影响,其变化呈现出分段趋势,无水采油期和高含水采油期变化规律并不一致。在低含水阶段,随着注入速度的增加,采出程度增加幅度近似于线性,由于降黏剂降黏、增稠调剖的作用,导致主流线方向的油水前缘较晚到达采油井,而注入速度越低,无水采油期越长,无水采出程度越高。在高含水阶段,随着注入速度的增加,采出程度增加幅度失去线性关系,当注入速度大于6 mL/min时,最终采出程度增加幅度开始降低。但较低的注入速度不利于油井时效,从生产实际出发,综合考虑经济等因素,在无水采油期采用较大的注入速度,但油井接近见水时,选用较小的注入速度延长无水采油期。

图16 不同注入速度下采出程度变化曲线Fig.16 Variation of recovery degree with different injection speed
3.5.4 注入方式对采出程度的影响
总注入量为1.5 PV,段塞注入量为0.6 PV,设计了5种降黏剂段塞注入方案(连续注入0.6 PV、8个0.075 PV、4个0.15 PV、2个0.3 PV、3个0.2 PV降黏剂段塞),以水驱方案作为基准,对比了5种注入方式下的采出程度。图17为三维数值模型不同注入方式下采出程度增幅的变化图。

图17 不同注入方式下采出程度增幅Fig.17 Increase of recovery degree under different injection mode
注入不同段塞大小的降黏剂溶液,高、低渗层采出程度均有不同程度提高。连续注入0.6 PV降黏剂溶液时,采出程度提高幅度介于方案2~方案5。对比方案2与方案3、方案4和方案5的结果可知,将0.6 PV的降黏剂溶液分段塞注入时,交替次数最多的方案2效果较差,对应模型的采出程度提高幅度只有8.9%。对比方案3、方案4和方案5的结果可知,段塞较大、段塞中降黏剂浓度较高的方案4采出程度增幅最大,达到14.5%。
4 结论
(1)结合油水两相控制方程、降黏剂传质方程及辅助方程,构建了浓度场-渗流场全耦合化学降黏驱替数学模型,获得了乳液黏度-含水率、降黏剂溶液黏度-浓度及降黏剂溶液与原油界面张力的辅助方程,建立了考虑降黏驱中各组分的对流-扩散-吸附的三维两相多组分渗流数学模型。
(2)采用具有有界性的高阶迎风格式克服了一阶迎风格式的不足,提高了浓度散度的计算精度,优选有限体积方法对模型求解提高了解的准确性,并对降黏驱数值模拟结果与岩心实验结果进行了验证,显示所建模型可以表征降黏剂的增黏和降黏效果。
(3)降黏剂驱油效果受注入浓度、注入方式、注入速度等因素的影响,研究中0.4%浓度的降黏剂采收程度提高幅度最大;合理注入量介于0.2~0.6 PV;推荐选用段塞较大、段塞中降黏剂浓度较高的方案;低流速有助于提高无水采出程度,延后见水时间,但不利于油井时效。高流速相同时间段内采出程度较高,但随着流速增大,采出程度增加幅度降低。故应根据油田自身产能设计确定最佳驱替速度。
