基于Chirplet变换在地震勘探时频域地层旋回变化识别分析
2023-12-15刘一灼汪勇桂志先
刘一灼, 汪勇*, 桂志先
(1.长江大学地球物理与石油资源学院, 武汉 430100; 2.油气资源与勘探技术教育部重点实验室(长江大学), 武汉 430100)
傅里叶变换是一种线性变换,针对实际地震波信号中更多的非线性问题,傅里叶变换明显作用有限。在这一问题的研究中,1946年Gabor首先提出了短时傅里叶变换(Short-time Fourier transform,STFT),可以在局部范围内对非平稳信号进行分析,经过后续研究表明该方法在实际测试中存在分辨率整体不高的问题[1-3]。在此基础之上,1986年由Mallat提出的连续小波变换(continuous wavelet transform,CWT),其本质是一种可调节窗口的傅里叶变换,在信号仿真过程中初端分辨率得到有效提高,但末端分辨率发散的问题依然存在[4-6]。而近些年提出的Chirplet变换(Chirplet transform,CT)是对短时傅里叶变换和连续小波变换的延申说明,由于其核函数不仅具有短时傅里叶变化和连续小波变换的时移、伸缩、时间和频率上的4种线性调频变换,还具备对核函数调制的特性,因此Chirplet变换对待分析信号在时频域分析中分辨率提升明显[7]。国外学者Zhu等[8]利用高分辨率勘探技术对Chirplet变换中的物性参数进行了对比分析,得出了不同取值下的Chirplet变换时频谱特征;Pukhova等[9]则是对Chirplet变换的波形上弦波和下弦波的展布特征进行了分析,得出了Chirplet变换在处理复杂波形的优势所在,国内学者田亚军等[10]、聂伟东等[11]对STFT、CWT以及CT几种时频分析方法在沉积旋回识别上的差异情况进行了分析,频率随时间的变化关系得到准确定量描述:频率随时间依次降低,代表地层层间厚度依次变厚,反之则代表地层厚度依次变薄。邱剑锋等[12]则是通过修改Chirplet变换中的核函数控制因子的取值,提高时间域的频次以此来增强Chirplet变换的整体分辨率。
在前人研究的基础之上,依据短时傅里叶变换、连续小波变换以及Chirplet变换的原理,现分别利用单分量和多分量仿真信号对3种变换进行测试,分析对比不同时频分析方法下的待分析信号频谱特征,同时再利用多分量仿真信号对原始Chirplet、所改进的2次Chirplet以及1.5次Chirplet进行测试,以此来突出在复杂时域波形中Chirplet变换的优势所在。随后利用改进后的不同频次的Chirplet变换对经过雷克子波与正负反射系数褶积后的混合旋回仿真信号进行测试,分析不同频次下的CT刻画沉积旋回薄互层准确位置的能力。同时针对塔里木地区工区一段特殊地震道下的地震信号进行分析,该道地震信号分布清晰且有一定规律,在该段地震信号中包含四组尺度不同的储层位,利用传统线性时频方法STFT、CWT以及原始CT和所改进后的变频次CT分别对该地震信号进行频谱分析,突出改进后的修改控制因子的Chirplet变换在应对实际地震勘探中的时频谱能量团集中度以及压制频散效果的优势,因此在后续地震信号分析中该方法应该受到重视与发展,以期为实际储层地震勘探提供理论依据支撑。
1 3种变换的应用要点
1.1 短时傅里叶变换
短时傅里叶变换由Gabor最先提出,针对传统傅里叶变换对非平稳信号局部信号区域时频分布无法进行分析的缺陷,短时傅里叶变换得以对其进行处理。由于所选择的信号相较于完整信号长度较短,因此该变换被称为短时傅里叶变换(STFT)。短时傅里叶变换的基本原理是:首先通过窗函数来截取给定平稳信号;再利用傅里叶变换处理窗内的信号,这部分的目标是准确定位测试局部信号时间内的频率变化;最后追踪信号定向时移传函数,即可准确获得这部分局域频率随时间的变化关系。简言之,变换过程首先对给定函数与窗函数进行褶积处理,对处理后的多元函数进行傅里叶变换,随即时移窗函数得到所需变换后的结果,即是短时傅里叶变换整个处理过程[13]。
已知信号z(t),其时域短时傅里叶变换为
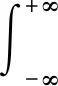
(1)
已知信号z(t),其频域短时傅里叶变换为
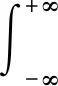
(2)
式中:z(t)为源信号;g(t)为窗函数;t为时间;f为频率。
利用式(1)、式(2)可推导得出短时傅里叶变换的逆变换为
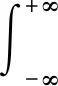

(3)
通过逆变换分析,短时傅里叶变换主要是利用参数τ来对信号进行描述时间、频率的变化关系,即通过小段信号来对整体信号进行描述。短时傅里叶变换的时窗控制范围为[u-η,u+η],其中参数η用来控制时频分辨率大小,因此短时傅里叶变换受限于固有的窗函数被选定,本身变换的矩形时频原子无法进行定量变化。
1.2 连续小波变换
连续小波变换1986年由Mallat所提出,与短时傅里叶变换的全区域变换所不同的是,该变换是在时频域局部限定区域进行的,因此,可以针对所研究的局域信号进行这部分信息的提取。连续小波变换的基本原理是:在傅里叶变换中,利用小波基函数的平移、伸缩等变化关系替代传统伸缩函数,替代后的时频变换就是连续小波变换。简单来说,连续小波变换实质是在传统傅里叶变换下其本身窗口可调节,但由于其小波窗内的信号与短时傅里叶让变换要求一致,必须是平稳信号,因而仍然存在传统傅里叶变换以及短时傅里叶让变换对信号的分析限制[14]。
已知信号z(t),其连续小波变换为
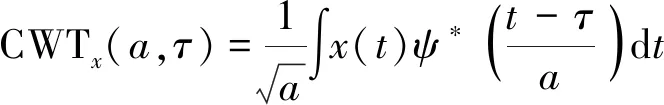
(4)
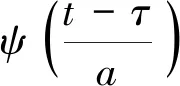
通过式(4)可知,连续小波变换主要是通过时移参数τ、尺度参数a来对整个变换进行控制和调节的,利用这两个主要参数,得到小波族函数为

(5)
通过小波族函数进行分析,该变换主要是由尺度因子a来控制基本小波的大小,参数a增大,时域带宽变小,频率增大。由于该变换时间随频率变化而变化,此类特性在应对二维信号分析中效果好于短时傅里叶变换,但该变换没有确切的限定值域限制时频域的增加或减少。
1.3 Chirplet变换
Chirp信号最早由Winkler于1962年提出,该信号由于是非平稳信号,因此又被命名为线性调频信号。而以线性调频信号为研究中心的Chirplet变换是一种新的时频分析方法,该变换本质上来讲是对短时傅里叶变换与连续小波变换两种变换的拟合,所以说可以看作是两种变换的推广[3,9]。由于Chirplet变换中所研究的对象是利用Chirp信号函数族与待分析信号的褶积计算得出,在褶积运算中同时运用了时间、频率以及单位尺度变化,这也再次证实了Chirplet变换是在短时傅里叶变换与连续小波变换的基础之上的一种线性变换的说法。Chirplet变换的基本原理是:利用对窗函数g(t)做时间上的平移和频率调制、对基本小波作平移和伸缩以及矩形时频原子在斜方向的拉伸与旋转变化这5种变化关系来对给定待分析信号进行的一种线性调频变换方式[12]。
给定一个函数s(t),Chirplet变换表达式为

(6)
式(6)中:s(τ)为给定函数;h(t)为族函数;参量t、f、a、c、d分别为时间、频率、伸缩量、时域上的线性调频、频域上的线形调频这5种时频变化关系。
通过对该变换的原理进行分析,该变换主要是通过将待分析信号投影到族函数中实现的,而族函数一般是通过修正原始窗函数得到的,窗函数一般都是选择压制频散效果较好的高斯窗函数,其表达式为
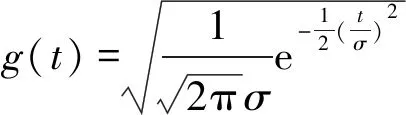
(7)
整个线性调频变换过程主要包括在时间上的线性调频以及在频率上的线性调频两部分,时间上的线性调频主要是利用线性调频信号chirp1与高斯窗函数进行乘积得到,表示为
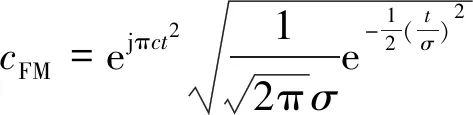
(8)
而频率上的线性调频主要是利用另一组线性调频信号chirp2与高斯窗函数进行乘积得到,表示为
(9)
因此,Chirplet变换的线性调频过程即核函数表示可以利用式(8)与式(9)的乘积后引入分析信号得到,即
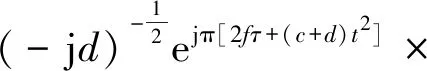
(10)
Chirplet变换对于解析信号的局部特性充分考虑,在重建非线性瞬时频率中去除误差效果很好。
1.4 分频次Chirplet变换
通过后续相关仿真结果可以得出,参数d在整个时频变换中是不进行相关计算的,因而Chirplet变换的线性调频表达式可简化为
(11)
由于Chirplet变换的主要变化就是在线性调频信号chirp也就是核函数中进行的,因此通过修改核函数增加核函数中的参数因子可以对整个变换进行有效改进
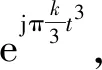
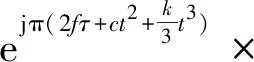
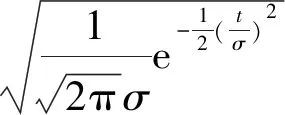
(12)

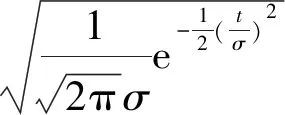
(13)
2 信号仿真测试
为了分析不同变换方法在对给定不同类型的待分析信号下的时频谱分辨能力以及压制频散效果,依次仿真了3类信号进行测试对比。
信号1:一次单分量仿真线性调频信号,s(t)=sin(2πut2)。
信号2:二次单分量信号,s(t)=sin(πut3)。
信号3:多分量线性调频信号,x(t)=cos[2π×(2t-t2+t1.5)]+cos[2π(3t-t2+3t1.5)]。
其中u=300,输入其他参量及参数选取为:采样频率fs=1 000 Hz、采样时间t=1 s、采样时间间隔dt=0.001 s。3种信号的时频域展布如图1所示。

图1 3种信号时域波形Fig.1 Three kinds of signal time-domain waveforms
对3种信号分别做短时傅里叶变换(STFT)、连续小波变换(CWT)以及Chirplet变换(CT)的时频分布对比如图2~图4所示。
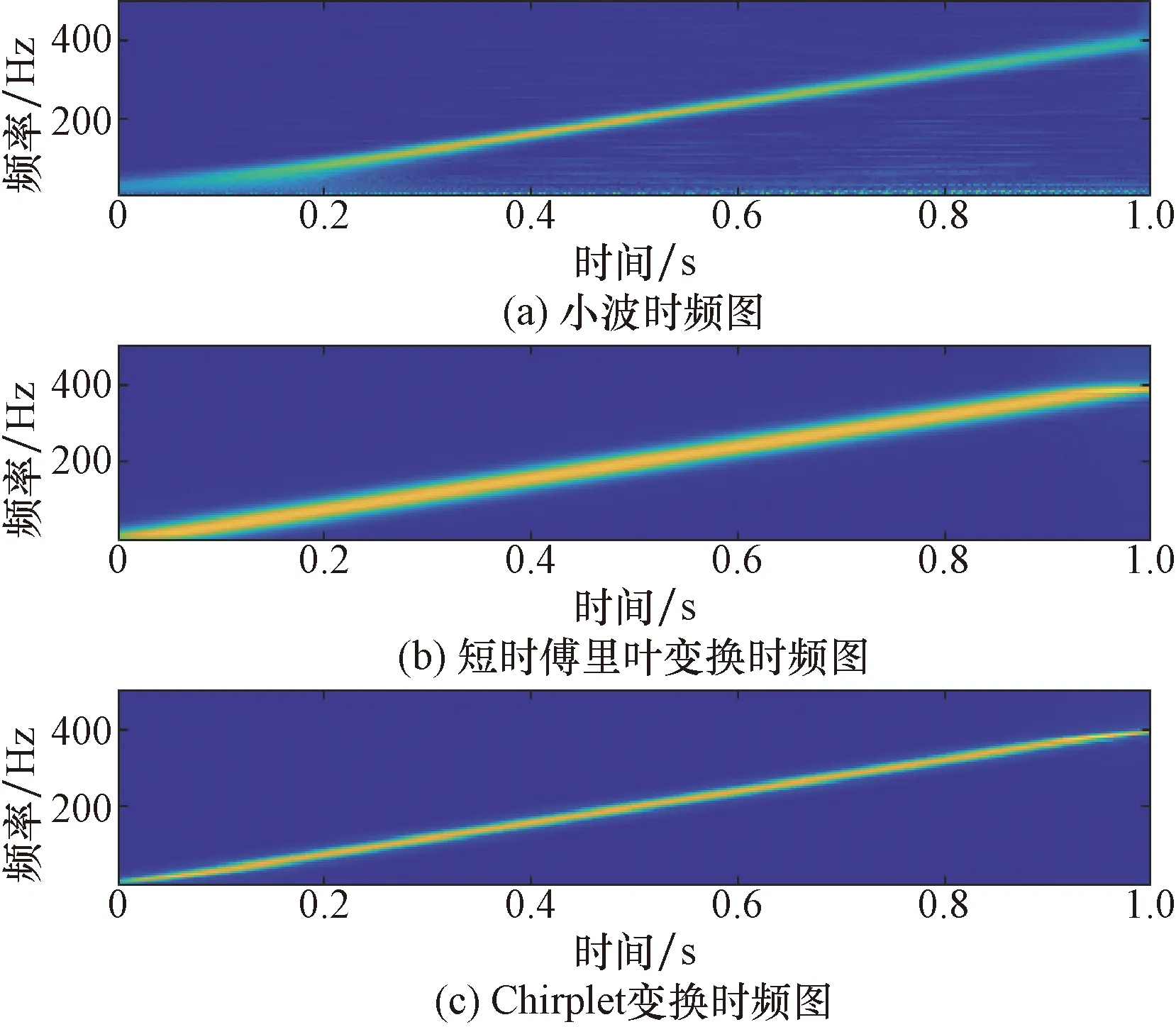
图2 信号1的3种变换时频对比图Fig.2 Comparison of three transformations of signal 1 in time frequency
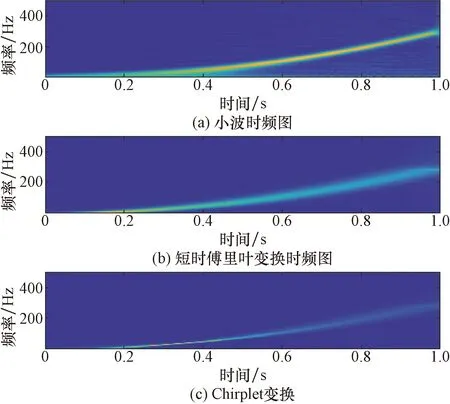
图3 信号2的3种变换时频对比图Fig.3 Comparison of three transformations of signal 2 in time frequency
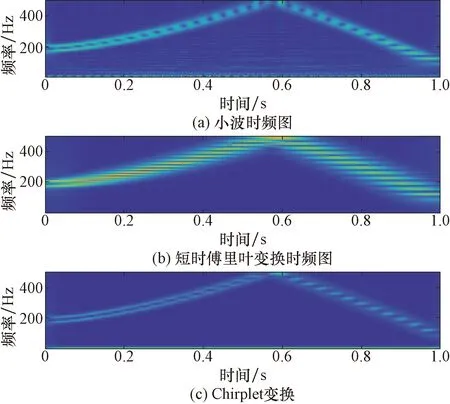
图4 信号3的3种变换时频对比图Fig.4 Comparison of three transformations of signal 3 in time frequency
从对给定单分量信号进行仿真测试结果来看,短时傅里叶变换(STFT)由于受到固定窗函数的制约,无法对本身时频原子进行有效变换,因此该变换下的待分析信号在时域分析中分辨率整体较低。连续小波变换(CWT)在时频分析中有高频部分频散严重这类情况,其有效分辨率也不是太高。而Chirplet变换(CT)更能对单分量信号的时间与频率相对变化关系进行准确描述,相比于短时傅里叶变换(STFT)以及连续小波变换(CWT),Chirplet变换(CT)在时域分析下能量分辨率最高。
对给定二次单分量信号进行短时傅里叶变换(STFT)、连续小波变换(CWT)、Chirplet变换(CT)可以发现,产生的差异变化基本与一次单分量信号相一致。由于知道地层层间走向通常是弯曲而非平稳的,因此选择地震信号要尽可能贴近于实际地质构造,二次分量线性调频信号相较于一次信号能更好地模拟实际地震信号时频域分布变化关系,二次信号时频变化带有角度弯曲这一特性,更符合地震信号在实际地下介质中的传播,更有利于进行此类数值模拟的研究。
从图4可以看出,在符合对单分量信号分析的特性同时,在对给定多分量信号分析中可以更加清楚发现,短时傅里叶变换下的时频域频散现象最为严重,连续小波变换其次,Chirplet变换压制频散能力相对最好,相对而言能更好地区分两个合成分量。所对应的Chirplet变换时频域分辨率最佳,连续小波变换次之,短时傅里叶变换分辨率最低,也就是说CT变换相较于其他两种时频谱方法更能对两组频率相近的信号进行有效的分辨。
为了更直观反映出修改核函数后的二次Chirplet变换、1.5次Chirplet变换与原始Chirplet变换的差异,因此对给定多分量线性调频信号分别做1次CT、2次CT和1.5次CT,其时频谱特征如图5所示。
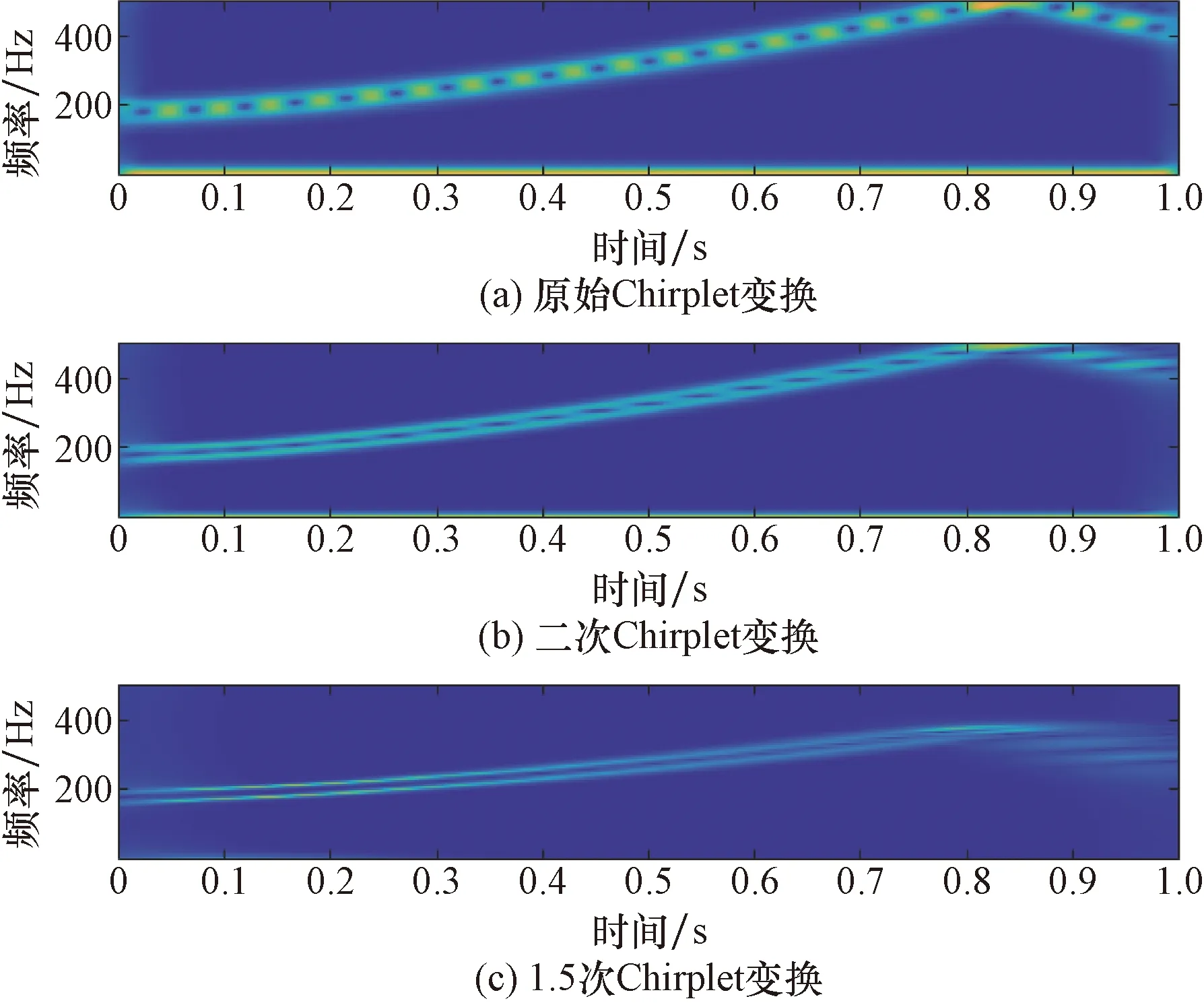
图5 信号3的不同频次的Chirplet变换时频对比图Fig.5 Comparison of Chirplet transform time frequency for signal 3 at different frequencies
从图5可以看出,在对给定多分量信号分析中可以清楚发现,3种不同频次的Chirplet变换在对两个分频信号进行分析中,原始Chirplet变换下的时频域频散现象最为严重,二次Chirplet变换其次,1.5次Chirplet变换压制频散能力相对最好,能更好地区分两个合成分量。所对应的1.5次CT变换时频域分辨率最佳,二次CT次之,原始CT分辨率最低,也就是说1.5次CT变换相较于原始CT变换以及二次CT变换更能对两组频率相近的信号进行有效的分辨[10-11]。
3 沉积旋回信号分析
对沉积旋回特征分析有助于更精准定位层序地层中的薄互层层间厚度变化的研究。沉积旋回信号的频率随着地层层间的厚度时刻发生变化,通常表现为:薄互层变厚,沉积旋回信号频率逐渐变小,反之薄互层变薄,沉积旋回信号频率随即变大。换言之,对沉积旋回进行准确分析是确定层序地层层间厚度的关键前提,而准确掌握地层的层间厚度变化对寻找油气藏意义显著。
3.1 叠加合成记录信号
通常采用传统子波与反射系数序列进行褶积,叠加合成混合型旋回信号。其中参量取值为:采样频率fs=1 000 Hz,采样时间t=0.7 s,采样时间间隔ds=0.07 s,这里选择主频f=50 Hz的雷克子波,反射系数序列选择正负相反的反射序列进行褶积处理,其中反射系数周期T=20个长度单元,每段间隔为1个长度单元,雷克子波、反射系数序列以及褶积模型如图6所示。
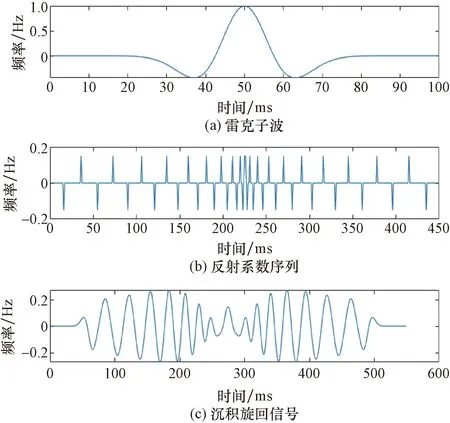
图6 构建褶积模型图Fig.6 Construct the convolution model
3.2 用于沉积旋回信号分析
对如图6所示得到的合成旋回信号记录,依次进行原始Chirplet变换、2次Chirplet变换、1.5次Chirplet变换,所得不同频次的CT时频谱如图7所示。
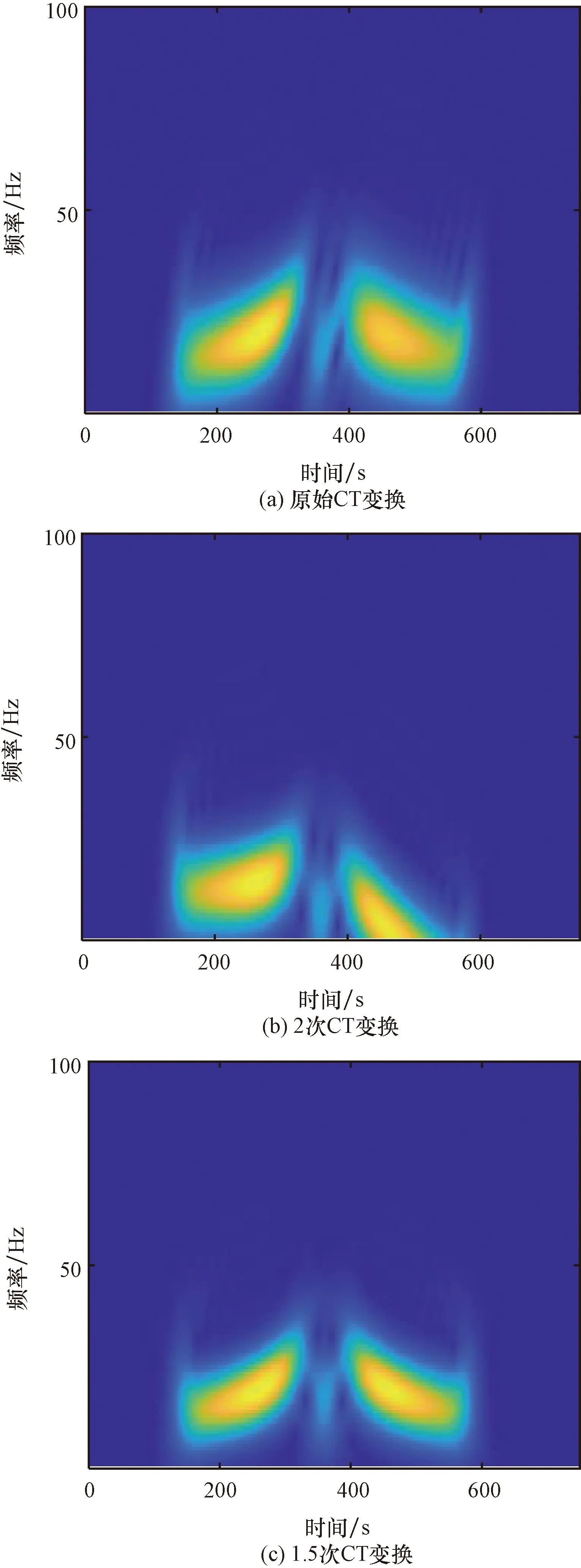
图7 混合旋回信号CT变换时频分布Fig.7 Time-frequency distribution of the original CT transformation of the mixed rotary signal
从以上分析可以看出,由于不同频次下的菱形时频原子表征物性参量数量级各不相同,这里1.5次Chirplet变换物性参数最为丰富,因此1.5次Chirplet变换相较于原始Chirplet变换和2次Chirplet变换,能量集中度最高,分辨率最强,同时沉积旋回信号旁瓣频散情况最低,更能准确观测出信号的频率随时间的变化趋势。通过对核函数中的曲率等物性参数在一定范围内进行调节可以对地层旋回变化趋势进行准确刻画,有利于地震勘探中对层间属性中的每一段薄层进行准确预测实际分布位置,为后续寻找油气提供帮助[15]。
4 实际地震信号应用
为了表明Chirplet变换及其改进的变频次的Chirplet变换在对沉积旋回储层检测的有效性,对塔里木1个实际工区的地震信号进行处理分析,在反复对比了该地区各道地震数据的情况后,某一地震道信号分布简单且对比度明显,该道地震道范围为8 000 m,整体振幅1 m,主要包含4个厚度大小不同的储层,储层厚度大致依次为800、400、200、100 m,该道实际地震道信号的时域波形如图8所示。
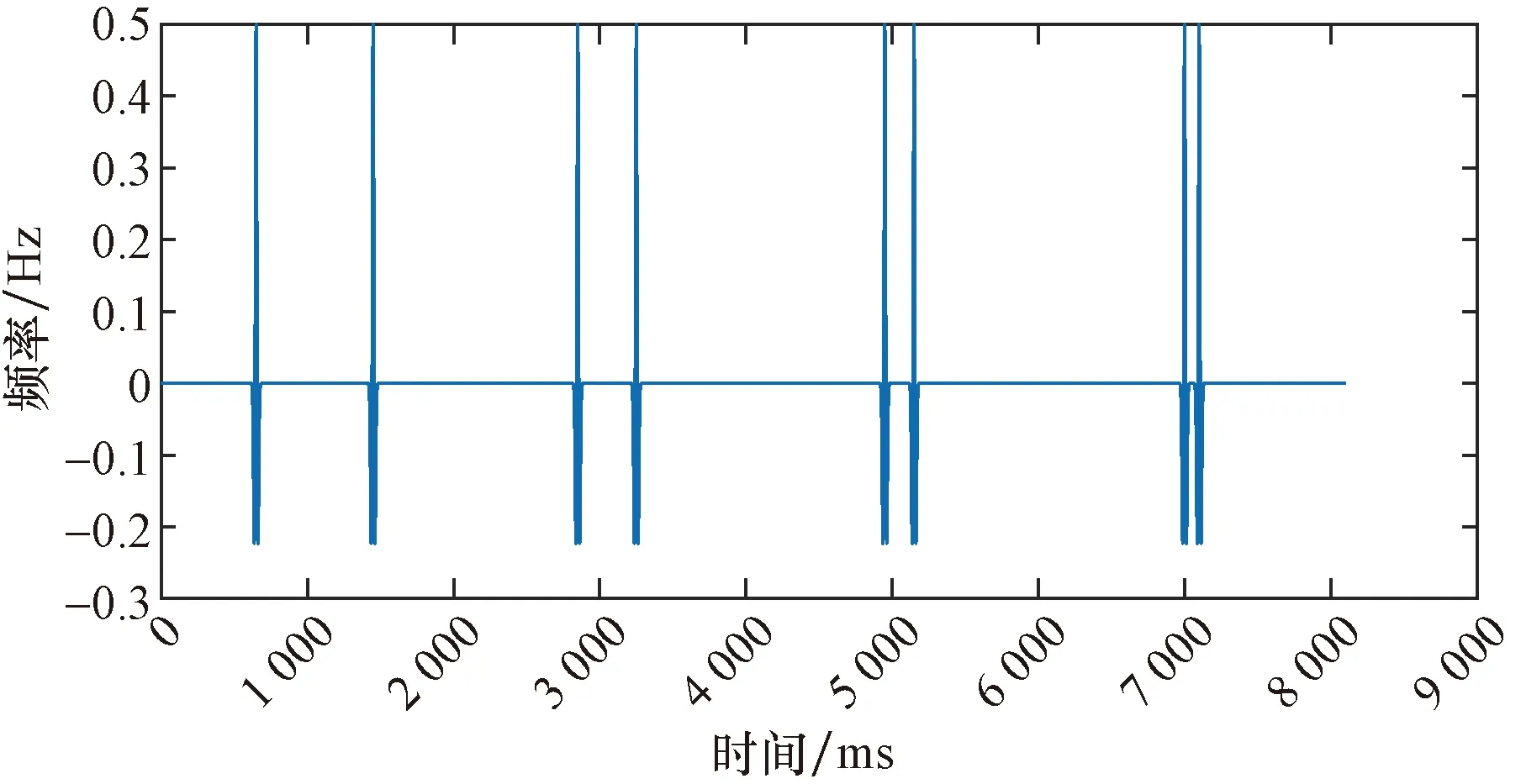
图8 工区地震道时域波形Fig.8 Time domain waveform of seismic channel in the work area
对该地震道时域波形依次做短时傅里叶变换、连续小波变换、原始Chirplet变换、2次Chirplet变换以及1.5次Chirplet变换,其不同方法的时频谱特征如图9所示。
通过对比在实际工区下的地震道信号做时频分析可以得出:短时傅里叶变换时频谱分辨率最低,能量保持相对最不集中,频散最为严重;连续小波变换时频谱可以对大尺度储层进行刻画,小尺度储层分辨率变低,出现频散现象和交叉项的干扰;原始Chirplet变换相较于两种线性变换分辨率提高明显,但对尺寸给临界刻画不够清晰,会出现对储层位置的误判;二次Chirplet变换在原始变换基础上,能量得到更加集中,储层分界面刻画更加清晰,只是在应对小尺度储层分辨率不是很高,会出现一定的频散问题;而1.5次Chirplet变换其分辨率最高,能量更加集中,无明显频散问题,储层边界刻画清晰,对于小尺度储层同样可以清晰识别。
5 结论
(1)分别对3种时频变换短时傅里叶变换、连续小波变换、Chirplet变换的基本原理进行了对照总结,并利用给定单分量、多分量信号仿真对3种变换进行控制变量分析,结果表明:Chirplet变换由于其特定的时频原子物性丰富度的优势,该变换相较于短时傅里叶变换、连续小波变换在时频分布下压制频散效果最佳,同时分辨率相对最高。
(2)分别对不同频次的Chirplet变换调频实际过程进行分析,对各自调频的核函数物性参数的差异进行对比描述,并再次利用给定多分量信号仿真对不同频次的Chirplet变换进行控制变量分析,结果表明:1.5次Chirplet变换由于对其调频核函数引入了曲率参量,时频分布下频率随时间的变化程度得到明显增强,在对多分量信号进行测试下,1.5次CT变换更能对频率相近的两组信号进行有利准确地划分,在不同频次下的时频分布关系1.5次CT变换分辨率最为出色。
(3)在实际应用中,利用雷克子波与反射系数序列进行褶积,得到混合沉积旋回信号,在前人仅针对短时傅里叶变换、连续小波变换、Chirplet变换下的混合旋回信号时频分布特征对比分析下,对3种不同频次的Chirplet变换进行定量对比分析,结果表明:1.5次Chirplet变换在分析沉积旋回信号具有比传统CT变换、2次CT变换分辨率高的优势,同时在旁瓣压制频散能力最强,时频域信号信息丰富度最全面。在实际对地震道信号进行时频谱分析中,改进的Chirplet变换分辨率更高,能量更为集中,压制频散效果明显,对储层尤其是小尺度尺寸给刻画清晰,因此1.5次CT变换可以更好地利用时频分布关系来确定薄层厚度变化趋势,为后续寻找油气层提供理论支撑。
