基于时变卡尔曼滤波的中途VSP钻前速度反演及在地层压力预测中应用
2023-12-15朱江梅高永德徐天鑫许晨旭王晓飞
朱江梅,高永德,徐天鑫,许晨旭,王晓飞
(1.中海油田服务股份有限公司 油田技术事业部,河北 廊坊 065201;2.中海石油(中国)有限公司 湛江分公司,广东 湛江 524057)
地震速度分析是地震勘探中一个举足轻重的参数,绝大多数地震勘探技术的核心任务本质上都是围绕着地层速度的勘测来进行的。而岩层的性质、岩石的成分、密度、 埋藏深度、地质时代、孔隙度、流体性质等众多因素则影响着地震波的速度传播,导致其预测和估计的复杂性和困难性,所以地震速度预测和估计成为备受工业界和学术界瞩目的核心技术。如何精确刻画和描述众多因素和地震速度之间关系,是准确进行地震速度预测的关键之所在。此外,地层速度预测正确与否又决定了地层压力预测的精度。
鉴于地震速度预测的重要性和困难性,各种各样的地震速度预测技术应运而生。我们可以从2个角度对地震速度预测方法进行综述:从采用的数据基础角度出发,可以分为3类:(1)地震资料为数据基础的叠加速度分析[1-3]、偏移速度分析[4-6]和层析速度反演[7-8]等速度预测方法;(2)以测井资料为数据基础的克里金估计[9-10]、随机模拟[11]和随机反演[12-13]等速度预测方法;(3)以井震资料结合为数据基础的井震匹配[14]、井震约束[15]等速度预测方法。从具体预测算法出发,可以分为2类:(1)基于模型的常规反演方法。在收集井震资料的条件下,利用地球物理知识,构建地震速度和各种观测要素之间响应数学关系,然后用反演方法求解地震速度。典型方法有:最小二乘反演[22]和波前反演[17]等。(2)前沿的深度学习方法。基于模型方法经常会利用地球物理知识引入众多假设和简化,导致地震速度求解性能受限于这些模型假设,这也是这么多年来地震速度预测的瓶颈之所在。最近受益于深度学习方法在诸多领域成功应用,人们利用深度学习方法以数据驱动方法来揭示构建地震速度和各种观测要素之间隐含关系,从而避免了遵循任意模型假设的局限。典型方法有深度递归神经网络方法[16]和卷积神经网络方法[17]。
毋庸置疑,现有方法对地震速度预测取得了很大进展,在工业界也取得了成功的应用[17]。但是,鉴于预测问题本身的复杂性和困难性,现有预测方法还存在以下缺陷:(1)现有模型方法主要存在的问题除了依赖模型先验以外,还存在为了线性化系统方程,导致无法容纳更多因素参与建模。求解的地震速度参数是固定而非时变的,也即常假设地震速度序列是平稳的。(2)深度学习方法虽然在有充足正确样本情况下能够接近理想的预测地震速度,但要获得足够样本在实际中是非常难的,甚至几乎不可能的。(3)现有方法的数据基础都是基于传统的叠前叠后地震数据,没有考虑前沿数据基础(比如VSP技术),虽然对于有些方法来说可以直接迁移,但是前沿数据基础其独特优点常常无法通过简单迁移得到充分发挥。
针对以上缺陷,本文提出了基于多元回归模型的地震速度预测方法,期望从以下几个方面来弥补现有方法缺陷,从而提升预测精度。具体贡献如下:(1)利用了新的数据基础,也即VSP数据。总所周知,VSP的走廊叠加数据具有比常规地震更高的分辨率,意味着潜在提供更高分辨率的预测。(2)VSP数据能够提供已钻井段的精确的时深关系,从而获得已钻井段的高精度的地层速度,同时获得比常规地震分辨率高的钻头前方的地层的反射波场信息,从而可以利用VSP数据反演获得钻头前方的地层速度。(3)毫无疑问,尽可能多因素的介入预测模型会带来更精确的预测结果,多元回归模型可以对多影响因素和地震速度之间关键建模,从而建立更精确的预测模型,而且回归模型可以在少样本条件下工作,从而适合VSP数据实际。(4)考虑到VSP具有更高分辨率,也意味着非平稳特性更趋强烈,对于多元回归模型求解我们采用时变的卡尔曼滤波器进行求解,鉴于时变卡尔曼滤波器是一个大类,考虑到求解问题实际(主要问题非线性和测量噪声的统计特性),具体使用无迹卡尔曼滤波来实现时变卡尔曼滤波过程,以追踪VSP数据和地震数据内在的时变特性。基于以上工作基础上,我们将地震速度预测应用在地层压力预测中,并实际应用在琼东南盆地高温高压井中,预测了钻头前方300 m的地层速度,进而估算钻头前方孔隙压力,为安全钻井提供了技术支持,验证了本文方法可行性。
1 预测问题描述与建模
1.1 预测问题描述
如前所述,本文目的是基于多元回归模型来反演得到中途VSP钻前速度。在构建多元回归模型之前,我们先来描述一下中途VSP钻前速度预测问题。对于中途VSP钻前速度预测问题,我们拥有的已知数据为VSP叠加走廊数据和对应的VSP时深关系。值得注意的是,VSP叠加走廊数据时间长度要大于VSP时深关系的时间长度,这意味着剩下时间的VSP井数据速度需要预测,这就是本文所需要完成的任务。
Y=h(X)+v
(1)
式中:v为上下样点值的速度差。
1.2 多元回归建模
如上所述,我们将公式的(1)钻头前方地层速度反问题求解问题转化为了有监督的回归问题,以解决公式(1)求解欠定性的问题。但是与单纯的回归模型不同的是,我们的VSP获得的地层速度是一个时间序列,互相时刻之间有关联的。而且这些关联性也有助于未钻井段地层速度的反演和预测,但是存在核心问题是如何对时间关联进行建模。
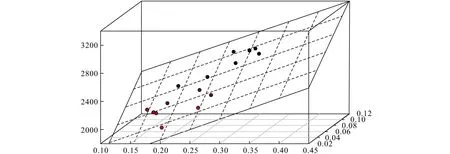
图1 多元非线性回归模型Fig.1 Multiple nonlinear regression mode
为了刻画时间之间的关联关系,我们引入了一阶马尔科夫链对其进行建模,也就是待估计速度序列之间为时间相关,可以用逼近函数f(·)表示,得到状态转移方程:
xk=f(xk-1)+rk
(2)
引入了时变关系之后,我们可以将公式(1)重写:
yk=h(xk)+vk
(3)
式中:yk代表叠加走廊以及各种衍生属性;xk代表系统是tk时刻的地层速度。值得注意的是,对于时刻tk而言此处为向量,这也是我们需要反演得到的结果;rk,vk分别代表过程噪声和测量噪声。由于在建模过程存在简化和近似,rk是时变建模过程中存在的误差。在这里主要是建模所产生的误差。vk是空间关系建模所导致的误差,当然也包括部分测量误差,所以这部分噪声相对比较复杂。公式(2)和(3)组成了我们所谓的系统状态方程,所以对其进行求解不能采用常规的反演方法,本文主要采用了基于卡尔曼滤波器的系统桩体求解方法进行求解,使得求得VSP速度能够同时满足以上2个方程。接下来我们对公式(2)和(3)构建详细的推导。
2 新的地层孔隙压力预测方法
2.1 基于无迹卡尔曼滤波器的VSP速度预测
为了求解公式(2)和(3),本文主要引入了无迹卡尔曼滤波器进行求解。值得说明的是无迹卡尔曼滤波器本身并不是我们的创新。我们创新在于创造性对VSP速度预测问题构建了多元回归模型,并为其设计了合适的求解算法,即无迹卡尔曼滤波器。选择无迹卡尔曼滤波器的原因是:一是对于多元回归模型求解最简单的方法是经典卡尔曼滤波器,通过对公式(2)和(3)的逼近函数和进行线性泰勒展开进行简化,但是这样简化无疑会引入更大误差,因为2个函数因为VSP预测问题内在复杂性导致非线性非常强,而无迹卡尔曼滤波器则避免了线性化过程;二是虽然避免以上问题,但是无迹卡尔曼滤波器还是继续了卡尔曼滤波的解析迭代求解优点,依旧具有简单高效的优点,这是其他系统状态方程求解方法所不具备的,比如粒子滤波器求解复杂,递归神经网络训练困难,深度学习样本要求多等缺陷。
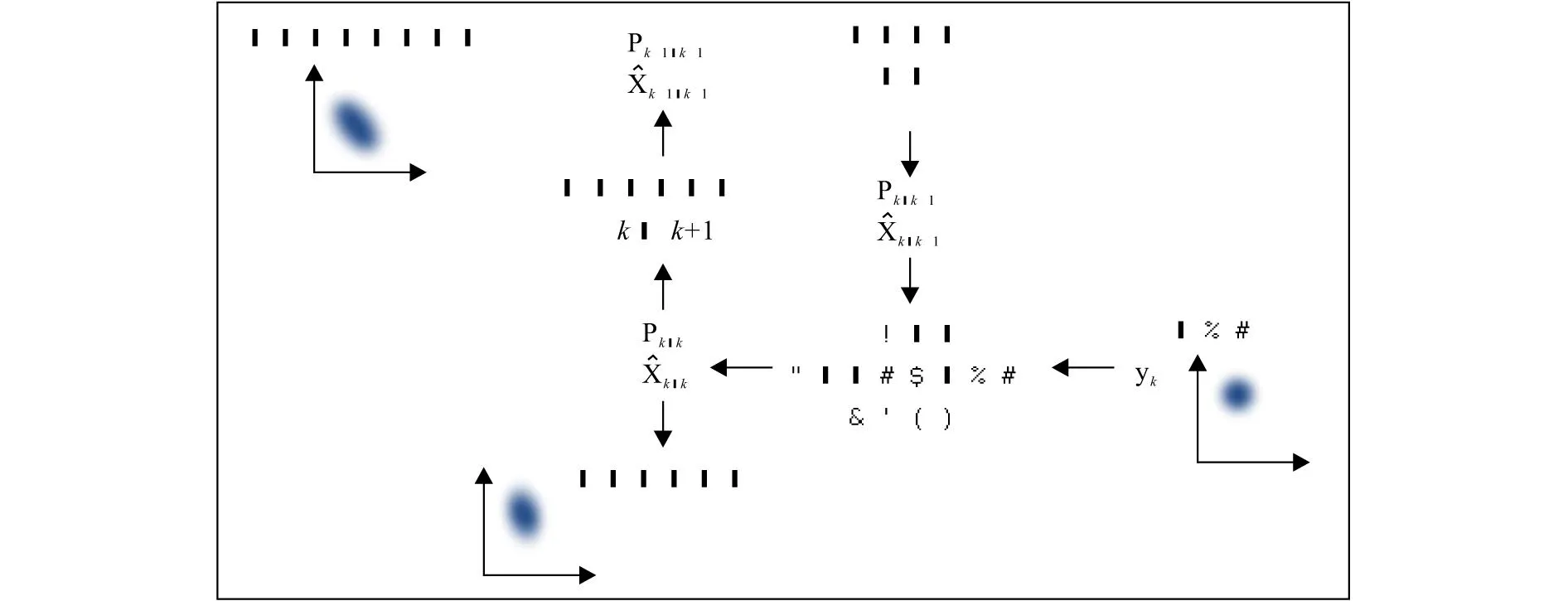
图2 卡尔曼滤波器示意图Fig.2 Schematic diagram of Kalman filter
基于以上认识,本文使用了一种无迹卡尔曼滤波器,即Unscented kalman filtering(UKF),将无迹卡尔曼滤波器直接求解公式(2)和(3),得到的相应的状态更新方程和测量更新方程分别为:
状态更新方程
(4)
测量更新方程
(5)
从公式(4)和(5)我们发现,VSP速度可以通过递归的方式进行求解,而且其递归方式是解析的,且整个计算过程为动态方式更新,也就是随时间变换而变化,意味可以追踪非稳定的VSP速度行为,而非传统方法常常假定VSP速度是平稳,服从某种确定性分布,比如高斯分布,从而通过估计确定性分布的参数来进行预测。所以卡尔曼滤波相对传统方法显著的优点是:可以将VSP速度预测放宽为非平稳的,这样放宽假设更符合预测实际,从而可以更有效提升预测性能。当然,从公式(4)和(5)得到另外一个显著优点其计算复杂度低,而且容易实现。
2.2 面向VSP速度预测的属性选择
Yopt=SFS(Y,X)
其优化策略为选择的属性产生回归结果与真实的VSP结果误差最小,其具体优化函数如下:
经过上述迭代优化过程之后,即可获得去掉冗余和无效属性的最优属性子集,从而可以有效提升VSP预测性能。
2.3 基于高分辨率速度的地层孔隙压力预测
地层的异常高压通常会导致地层速度的减小,因此层速度同时也可以作为地层压力预测的关键资料。目前,利用层速度资料计算地层压力的方法主要有:Eaton法、等效深度法、Bowers法、Fan简易方法、Fan综合解释法、Fllippone法等。但在地层还未钻开之前,或者缺少测压资料时,Eaton法是通过泥岩速度趋势线控制进行孔隙压力预测,是一种简便易行且常用的方法。本次研究在利用VSP数据精确反演钻头前方的地层速度的基础上采用Eaton法来进行地层压力预测研究。
Eaton法是一种基于正常压实趋势线计算地层压力的方法,它利用正常压实地层段建立正常趋势线,通过实际地层速度与趋势线速度的比值来计算地层压力。
(6)
式中:Pp为地层孔隙压力;Po为上覆岩层压力;Ph为正常的静水压力;Vn为地层正常压实时的速度;V为实测地层速度(未钻地层的速度为预测地层速度X);N为Eaton指数。
2.4 具体算法步骤
本文的提出的算法具体步骤如下:
输入:已钻井段地层速度Y,VSP走廊叠加,
2.回归模型训练:将最优属性集Yopt和已钻井段地层速度Y输入卡尔曼滤波器进行训练,得到回归模型xk=f(xk-1)+rk和yk=h(xk)+vk

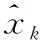
至于影响该算法最关键因素主要有4方面因素:一是地震属性的完备性,主要是对VSP预测所需要的属性是否能够充分,是否存在因为属性缺失而导致的信息丢失;二是属性选择性能,属性选择是NP难问题,无法获得最优解,只能使用贪婪算法获得次优的性能,所以本文选择SFS算法无法获得最优性能,这也会影响性能;三是回归模型训练的线性化建模误差,由于采用了简单高效的卡尔曼滤波求解方法,而卡尔曼滤波在求解过程中采用了2次泰勒展开线性化操作,无疑为引入建模误差;四是训练样本不足,由于是有监督回归问题,势必需要有足够训练样本才能取得满意效果,样本不足无疑会影响性能,这也地球物理许多机器学习问题的通病。以上4方面因素交织在一起共同影响了最后VSP预测性能,同时也从另外一个方面反映出了VSP预测的困难性。确定了VSP反演预测的速度后,就可以使用Eaton法求解地层压力,其具体输入主要就是VSP预测速度和其它几个参数,这些也构成了压力预测的影响因素。
3 实际应用
本方法在琼东南盆地Y23-A井的钻探过程中获得了成功应用。琼东南盆地位于南中国海北部陆缘张裂大陆边缘的西端,具有东西分块、南北分带构造格局[23],目前已发现了陵水17-2、陵水25-1、陵水13-2、崖城27-2多个气田或含气构造。崖城23邻近陵水、崖南2大富生烃凹陷,并且构造在深入陵水凹陷的大型构造脊上。崖城组发育砂岩输导体系,处于泄压区,陵水凹陷生成的油气可沿构造脊向该目标运移,具有高效油气聚集的条件。但同时,工区内发育大量NW走向断层[24],构造复杂,导致地下压力体系复杂,在钻井的过程中,需要进行孔隙压力的监预测工作[25]。
Y23-A井的目的层段为崖城组,周边的邻井距离都比较远。最近的一口井Y24-A井也已经是7年以前采集的,距离Y23-A井17.25 km,在黄流组下部(测深3 500 m)速度开始有降低趋势,表明孔隙压力系数开始增大;梅山组测井结果表明在测深3 950~4 000 m处孔隙压力系数达到了1.85,该井未钻到三亚组和崖城组。也就是说,该井提示了在本区域梅山组的孔隙压力系数约为1.85,但三亚组和崖城组的压力情况未知。另外一口邻井Y21-D井,为22年以前采集的,距离Y23-A井30.16 km,这口井钻到了崖城组,并在三亚组和崖城组测量了声波资料。同时,地震剖面上显示,两口井在进入崖城组后,波阻特征都呈强反射特征(如图3蓝色框内所示)。因此,可以借助Y21-D井崖城组的声波资料进行区域地震P波速度反演,抽取Y23-A井的井旁数据作为Y23-A井在三亚组和崖城组未钻井段VSP数据反演时的低频速度控制趋势。然后通过Y23-A井VSP数据反演获得钻头前方的速度,进而预测钻头前方的孔隙压力变化情况。
根据Y24-A井在梅山组的测压数据,Y23-A井梅山组到三亚组之间的钻井过程中泥浆比重逐渐由1.80 g/cm3调整至1.85 g/cm3,在钻到三亚组测深4 183 m时发生井漏,此时的钻井泥浆比重为1.85 g/cm3。钻前根据地震数据解释速度预测前方地层的孔隙压力系数会达2.07~2.15,因此后续钻井的泥浆比重如何调整成为钻井决策的难点。在如此复杂的井况下,依据地震信息预测的孔隙压力系数的精度无法满足安全钻进的要求,于是决定进行中途VSP测量并进行速度反演及孔隙压力预测,对前方地层的速度进行反演预测进而估算压力系数。
本次预测首先以邻井Y21-D(图4-A),本井(Y23-A)测深4 180 m以上的随钻声波(图4-B)结合地震数据进行波阻抗反演建立了所需的低频速度模型(图4-B第一列)所示。这样,在纵向上通过本井已钻井段的测井数据,横向上借用Y21-D及地震数据的波阻抗反演获得信息为下一步VSP速度反演建立了相对可靠的低频控制趋势。
在VSP资料处理完成后,从图5可以看到,VSP的走廊叠加道相比地震纵向分辨率明显提高,利用本文的方法进行了速度反演,获得了钻头前方(测深4180~4430m)地层速度的预估值(图5中右边倒数第二列的绿线),并预测了钻头前方(测深4 180~4 330 m)的孔隙压力系数约1.8~2.0 g/cm3,4 400 m附近孔隙压力系数将达到2.22 g/cm3(图5中右边倒数第一列的粉色线)。实钻表明,本文方法预测的速度与实钻后其他服务公司根据电阻率拟合的声波趋势吻合较好。实际测压取样表明,测深4 350~4 423 m的孔隙压力系数为2.25 g/cm3,预测误差仅为0.03 g/cm3。 结果表明本文方法可行,反演的速度相对可靠,可以用于未钻地层的压力预测。当然随着预测距离的加大,且地层压力增大,使得VSP走廊叠加的分辨率降低,预测误差也会随之增大。

图4 邻井Y24-D井的测井数据(A)及Y23-A井已钻井段随钻数据(B)和低频速度模型Fig.4 Logging data of adjacent Well Y24-D and data while drilling and low-frequency velocity model of drilled section of Well Y23-A
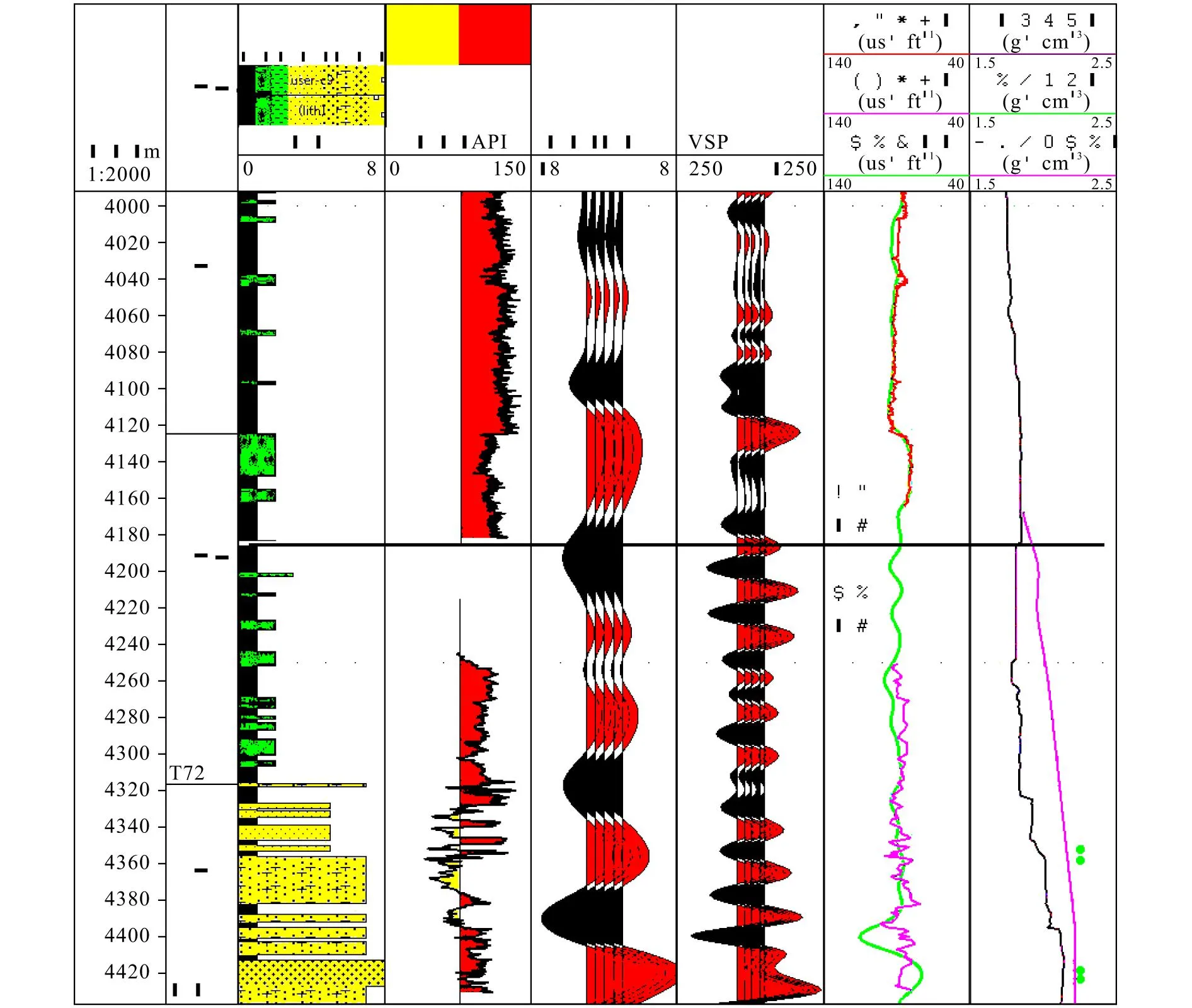
图5 Y23-D井速度反演预测及压力预测与实钻结果对比Fig.5 Velocity inversion prediction and pressure prediction of Well Y23-D compared with actual drilling results
4 结 论
本文提出了基于卡尔曼滤波的VSP速度预测方法,核心贡献是将多种因素以属性方式融入到多元回归模型中,并通过卡尔曼滤波器来求解该多元回归模型,并利用VSP在已钻井段的时深关系及钻头前方未钻井段反射波场信息进行钻头前方地层速度的反演预测。基于以上工作基础上,进一步将预测的钻头前方的地层速度结果应用在地层压力预测中,具体通过南海琼东南盆地Y23-D井的实际验证了本文方法的准确性,即本文方法预测得到的地层速度与后续实钻结果吻合度较好,可为海上油气勘探中中深地层高温超高压地层勘探所面临的钻井工程风险问题提供高精度钻前地层速度支撑,用于钻头前方地层的孔隙压力预测。
