Calibration of quantitative rescattering model for simulating vortex high-order harmonic generation driven by Laguerre-Gaussian beam with nonzero orbital angular momentum

Jiaxin Han(韩嘉鑫), Zhong Guan(管仲), Beiyu Wang(汪倍羽), and Cheng Jin(金成),2,†

1Department of Applied Physics,Nanjing University of Science and Technology,Nanjing 210094,China

2MIIT Key Laboratory of Semiconductor Microstructure and Quantum Sensing,Nanjing University of Science and Technology,Nanjing 210094,China

Keywords: high-order harmonic generation, quantitative rescattering model, time-dependent Schr¨odinger equation,macroscopic propagation,orbital angular momentum,Laguerre-Gaussian beam

1.Introduction

Optical vortex carries the orbital angular momentum(OAM), which has been demonstrated by a Laguerre-Gaussian (LG) laser beam by Allenet al.in 1992.[1]Such beam appears as an annular ring with the zero on-axis intensity and is specified by the topological chargel, characterizing the phase dependence of exp(ilφ), and byp, associating with the number of the radial node.Thus it carries an OAM ofl¯hper photon, where ¯his the reduced Planck constant.Due to the vortex light beam with the helical phase that possesses a spiral wave front, it has been applied to numerous different fields, including optical manipulation,[2]quantum information processing,[3]particle manipulation,[4,5]optical communications,[6]phase-contrast interferometry,[7]and so on.It has also been employed in observing the transfer of OAM to matter,such as in atomic and molecular systems.[8-11]

While it is relatively straightforward to generate vortex light beams with nonzero OAM by optical elements in the infrared(IR)and visible ranges,[12]similar technology is much more difficult to create vortex beams in the extreme ultraviolet (XUV) and soft x-rays (SXR).[13]However, as a wellknown strong-field phenomenon,[14-17]using high-order harmonic generation (HHG) from gaseous medium, i.e., an upconversion nonlinear process, the OAM beam can be converted from the IR to the XUV and SXR.[18-28]For instance,in the first experiment,in 2012,Z¨urchet al.[18]measured lowcharged XUV vortices whose topological charges do not scale with the harmonic order.In 2014, Gariepyet al.[20]interferometrically determined that each harmonic carries the OAM and evidenced that the azimuthal phase of each harmonic isqtimes (qis the harmonic order) than that of the driving laser.The OAM of XUV beam can be tuned when two-wave mixing is applied in a non-collimated scheme,which has been demonstrated by Konget al.[29]and Gauthieret al.[30]in 2017, respectively.The conservation law of angular momentum in the generation of vortex HHG has also been examined in other theoretical studies.[19,26,31]A fully theoretical description of experimentally measured vortex harmonics generated in a gas medium consists of two parts: (i)the generation at the singleatom level; and (ii) the propagation of high-harmonic field in the macroscopic medium, including its propagation in free space.

The single-atom response of HHG has been well understood intuitively by the three-step model[32,33]and can be precisely obtained by solving the time-dependent Schr¨odinger equation(TDSE).[34]On the other hand,for simulating macroscopic HHG, single-atom induced dipoles need to be calculated for a number of peak intensities to insert into the Maxwell’s propagation equations, accounting for a nonuniform intensity and phase distribution of a focused laser beam.Thus, calculations based on the single-atom TDSE are very time consuming and are rarely adopted for simulating the macroscopic HHG.Alternatively,single-atom induced dipoles calculated using the strong-field approximation(SFA)are often used in the theoretical investigations of the macroscopic propagation effect.[35,36]However, the limitation of SFA for the description of single-atom response is well known.[37]To improve the SFA,a quantitative rescattering(QRS)model has been developed by Lin’s group,[38-40]which is simple, timesaving, and accurate.In the QRS, it applies the approximate factorization for the induced dipole driven by a linearly polarized laser pulse,which can be written as a product of a returning electron wave packet and a photorecombination transition dipole moment.Since the recombination dipole moment can be accurately calculated in a time-independent manner, the calculation of single-atom HHG spectra by the QRS is about as fast as the SFA and the results are nearly as accurate as those obtained from the TDSE.[41]Therefore, the QRS-based induced dipoles have been widely adopted to simulate the macroscopic HHG without the OAM in our previous studies.[42-44]The validity of this approach has been checked against results with TDSE-based induced dipoles.[45]However, it is not clear if the replacement of the TDSE with the QRS in the single-atom response can still be valid when simulating the macroscopic vortex HHG driven by the nonzero OAM beam.

Our goal in this paper is to examine the macroscopic vortex HHG with QRS-based induced dipoles against those simulated by the single-atom TDSE-based response.We will systematically compare the results from two methods,for integer and non-integer harmonics and under different macroscopic conditions.Note that such comparison for vortex high harmonics has not been performed in the previously published works.This paper is organized as follows.In Section 2,we will briefly introduce the propagation equations and Huygens’ integrals for simulating macroscopic vortex HHG and the formulation of LG beam.And in Section 3 we will present two methods, i.e., the TDSE and the QRS,for simulating the single-atom induced dipole in short.In Section 4,we will first compare HHG spectra using the TDSE, QRS, and SFA, we will then compare intensity and phase distributions of integer and non-integer harmonics simulated by the QRS and TDSE,and we will next check the difference in the macroscopic results by varying the gas-jet position relative to laser focus,and we will finally provide physical explanations in terms of the time-frequency analysis.The conclusions will be given in Section 5.

2.Theories of harmonic propagation and driving laser

2.1.Propagation equations of high-harmonic field

In our simulations,we assume that the fundamental beam with the OAM is not modified within the ionized gas medium,i.e.,it propagates as in free space.We only consider the conditions of low gas pressure and low laser intensity.Details of the propagation of a vortex high-harmonic field can be found in Ref.[45].In the frequency domain,it is described in a Cartesian coordinate by[46-50]

Here ˆFis the Fourier transform operator acting on the temporal coordinate,andPnl(x,y,z′,t′)is the nonlinear polarization,which can be calculated as

Heren0is the neutral atom density,ne(x,y,z,t)is the free electron density, andw(τ) is the tunnel ionization rate.The induced dipole momentD(x,y,z,t) is calculated for each atom in the medium.

The high-harmonic field obtained at the exit plane of the gas medium (z′=zout) is called a near-field one, and the total HHG power spectrum is obtained by integrating over the transverse plane

2.2.Far-field harmonic emission

Near-field harmonics are propagated and divergent in vacuum until reaching the detector.These harmonics far away from the gas medium are called far-field ones.Far-field harmonic emissions can be obtained from near-field ones(located atzout)using Huygens’integral under the paraxial and Fresnel approximations(in a Cartesian coordinate)as

whereL=zf-zout,zfis the far-field position from laser focus,xfandyfare the transverse coordinates in the far field,and the wave vectorkis given byk=ω/c.

2.3.Fundamental Laguerre-Gaussian beam

For the driving laser beam with the OAM,we consider an LG mode.Under the paraxial and slowly varying transverse amplitude approximations, its electric field can be expressed in a cylindrical coordinate as[31]

3.Theories of single-atom response

In this work, the driving laser carries a small OAM and its size is about tens of micrometers in the laser-gas interaction region, thus an atom cannot feel the tiny change in the phase of the OAM beam upon variation of azimuthal angle.In the single-atom response, each atom interacts with a local electric field at a given spatial position of the OAM beam.The laser-atom interaction can be treated under the dipole approximation.[51]In principle, one can calculate the induced atomic polarization or dipole acceleration by numerically solving the time-dependent Schr¨odinger equation(TDSE), which can then be inserted as a source term in the propagation equation.Alternatively, the QRS model is commonly used, which greatly improves the strong-field approximation (SFA) (or the Lewenstein model).Here we focus on the QRS and the TDSE.

3.1.Quantitative rescattering model

For a linearly polarized laser,single-atom induced dipole momentD(t) can be accurately calculated by using the QRS model.[52,53]Based on the three-step model, the QRS model improves the SFA,and it can give the harmonic intensity distribution in the whole spectral range nearly as accurate as solving the three-dimensional (3-D) TDSE.[45]Note that the analytical formulation of induced dipole moment has been derived by the TDSE in the length gauge under the SFA.[37]In the QRS model, the length gauge is employed, and the induced dipole momentD(t)is transformed into the frequency domain,which can be written in a separable form as[52,54]

whereNis the ionization probability taken at the end of the laser pulse,d(ω) is the complex photorecombination (PR)transition dipole matrix element, andW(ω) is the complex returning electron wave packet.

The propagation of ionized electrons before the recombination, i.e., the second step in the three-step model, is governed mostly by the laser field while the electron is far away from the target ion.This process can be fully described by the SFA,so the reduced electron wave packet by the SFA is

In the QRS model,the plane wave used in the SFA[37]for calculating the PR transition dipole is replaced by an accurate scattering wave, while the electron wave packet remains the same as that in the SFA.Thus, one can practically obtain the induced dipole moment as

where bothDsfa(ω)anddqrs(ω)are complex numbers,whiledsfa(ω) is either a pure real or pure imaginary number.Nqrsis calculated by using the ADK theory.[54]Within the singleactive electron (SAE) approximation,dqrs(ω) can be calculated by using exact numerical wave functions for the bound and continuum states, which can be obtained by solving the time-independent Schr¨odinger equation with a given atomic potential.

3.2.Time-dependent Schr¨odinger equation method

In the TDSE, atomic potentialV(r) of Ar atom can be expressed as[55]

whereZcis the charge seen by the active electron asymptotically anda1,...,a6are parameters obtained by fittingV(r)to the numerical potential from self-interaction free density functional theory.The accelaration gauge is chosen and the laser is linearly polarized.In terms of the complete set of eigenstatesfnl(r)Ylm(ˆr)ofH0=-∇2/2+V(r),the time-dependent wavefunctionΨ(r,t)can be expanded as

HereYlmfunctions are the spherical harmonics, and radial eigenfunctionsfnl(r)are often expanded in terms of some basis sets,like the discrete variable representation functions.

4.Results and discussion

In our simulations, we take the fundamental laser pulse to be an LG1,0beam, i.e., the vortex beam carries the OAM of ¯hand doesn’t have the radial node.We choose the beam waist at laser focus asw0= 25 µm and the laser wavelength as 800 nm.The Rayleigh length is about 2.5 mm, defined aszR=πw20/λ, whereλis the laser’s central wavelength.In the time domain,we assume that the laser pulse has a cosinesquared envelope, its full-width-at-half-maximum (FWHM)pulse duration is 19.4 fs,and its carrier-envelope phase(CEP)is set as 0.A 1-mm-long Ar gas jet with constant density is placed at 2 mm after,at,or before the laser focus,respectively.The peak intensity at the center of the gas medium is always fixed at 1.5×1014W/cm2.

4.1.Comparison of total vortex harmonic spectra from TDSE,QRS,and SFA

Fig.1.(a)Simulated macroscopic harmonic spectra of Ar from the TDSE(purple line), the QRS(green line), and the SFA(orange line)(from top to bottom for low-order harmonics).A 1-mm-long gas jet is placed at 2 mm after the laser focus,and the peak intensity at the center of the gas medium is fixed at 1.5×1014 W/cm2.(b)and(c)Comparison of vortex harmonic spectra by the TDSE(purple line)and the QRS(green line)using linear scale,where the spectra are normalized at 17th harmonic(H17)and H33,respectively.

We first show the integrated yields of macroscopic vortex HHG of Ar in Fig.1(a).The gas jet (specifically, its center)is placed at 2 mm after the laser focus.The harmonic emissions at the exit plane are integrated over the radial direction.Single-atom induced dipoles are calculated by three different approaches:the TDSE,the QRS,and the SFA.The spectra are normalized at the cutoff and are plotted using a logarithmic scale.Compared to the HHG spectra of the TDSE, the SFA gives the correct predication only in the cutoff region,beyond H25, and it fails for low-order harmonics.The QRS shows a much better agreement with the TDSE over the entire spectral region.We also compare the results of TDSE with those of QRS on a linear scale.If we choose H17 or H33 to normalize the harmonic yields from two models, one can see that in two respective spectral regions, the spectra of the QRS agree well with that of the TDSE, see Figs.1(b) and 1(c).So the QRS is able to greatly improve the vortex HHG by the SFA,and achieves the similar results to the TDSE,but with computational effort close to the SFA.

4.2.Comparison of spatial intensity and phase distributions of high harmonics from TDSE and QRS

For the high harmonics from the TDSE and the QRS above,we take a close look at their spatial intensity and phase distributions both in the near and far fields in Figs.2-4.Note that the gas jet is put at 2 mm after the laser focus.In Figs.2 and 3,we show the results for three selected integer harmonics,two in the plateau and one in the cutoff.And in Fig.4,we show the results for three fractional high harmonics(FHHs)in the plateau and in the far field.

Let us compare spatial intensity profiles of H15,H23 and H31 in the near field first.The harmonic intensities from the TDSE are primarily distributed over one single ring, and the ring for the plateau harmonic is wider than that for the cutoff one, see Figs.2(a)-2(c).The spatial intensity profiles from the QRS have the same features as those from the TDSE,see Figs.2(g)-2(i).We then compare corresponding spatial phase distributions of harmonics.The phase from the TDSE changes rapidly along the azimuth angle,revealing that the topological charge of harmonic is its orderqtimes the fundamental one as shown in Figs.2(d)-2(f).And the phase results from the QRS almost exactly reproduce that from the TDSE for three different harmonic orders as shown in Figs.2(j)-2(i).Thus, the QRS reasonably resembles the TDSE in simulating both spatial intensity and phase profiles of different integer harmonics in the near field.

We next look at the spatial intensity and phase distributions of three harmonics in the far field.The intensity profile from the TDSE shows the one major ring structure and the radius divergence does not change with the harmonic order, see Figs.3(a)-3(c).The QRS almost gives the exactly same intensity profiles by comparing the results for three harmonic orders, see Figs.3(g)-3(i).The comparison of phase distributions of H15, H23, and H31 from the TDSE and the QRS indicates good agreement with each other, as shown by comparing Figs.3(d)-3(f)with Figs.3(j)-3(l).Therefore,the perfect agreement can be achieved between the QRS and the TDSE when the results of integer vortex harmonics are compared in the far field.Note that the slight difference between two methods occurring in the intensity distribution in the near field can be eliminated in the far field.

Fig.2.Intensity and phase distributions of integer high harmonics in the near field(at the exit plane of the gas medium)calculated by employing the TDSE (a)-(f) and the QRS (g)-(l), respectively.First row: 15th-order harmonic (H15); second row: H23; third row: H31.The harmonic intensity in each figure is normalized separately.The gas jet is placed at 2 mm after the laser focus.Phase values are removed if corresponding intensities are smaller than 30%of maximum intensity.

Fig.3.Similar figure to Fig.2,but spatial intensity and phase distributions are plotted in the far field.

We then show the spatial intensity and phase profiles of fractional high harmonics (FHHs) from the TDSE and the QRS in the far field, see Fig.4.Note that the FHH carries the non-integer OAM, which plays an important role in the generation of a helical attosecond pulse train with azimuthalangle dependence.[56]For the harmonic intensity results from the TDSE,there are few radial gaps (or minimum structures)in the ring-like intensity distribution, thus unlike the integer harmonic, it does not have the cylindrical symmetry, see Figs.4(a)-4(c).For the QRS ones,the ring-like structure and gap structures can all be accurately duplicated for different harmonics, see Figs.4(g)-4(i).When it comes to the spatial phase distribution,the discontinue feature along the azimuthal angle can be clearly identified.This feature does not depend on the harmonic order and is about the same for the TDSE and the QRS results,as shown by the comparison of Figs.4(d)-4(f)and 4(j)-4(l).So the QRS is able to reproduce all features in the intensity and phase distributions of FHH from the TDSE.

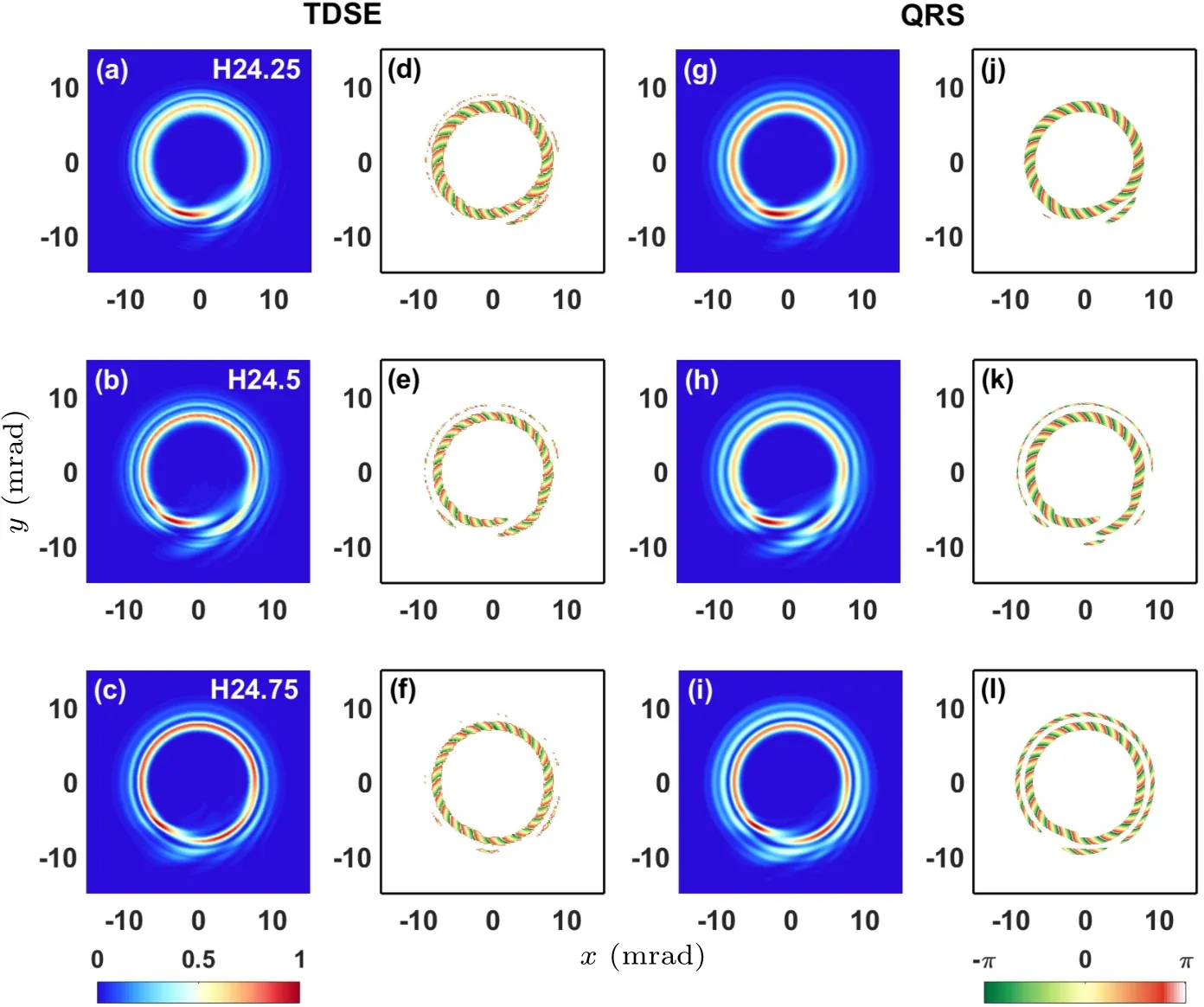
Fig.4.Same as Fig.3 except that three fractional harmonic orders are considered.

4.3.Comparison of vortex high harmonics from TDSE and QRS by varying the macroscopic condition

Fig.5.Transverse profiles of intensity(first and third columns)and phase(second and fourth columns)of H23 from the TDSE(left two columns)and the QRS(right two columns).First row: near-field results;and second row: far-field ones.The gas jet is put at the laser focus.

Fig.6.Same as Fig.5,but the gas jet is located at 2 mm before the laser focus.

All results above are obtained when the gas jet is put after the laser focus.Can the agreement between the TDSE and the QRS be maintained if the position of gas jet is greatly varied with respect to the laser focus? We thus first locate the center of the 1 mm long gas jet at the laser focus.The results for H23 are shown in Fig.5.In the near field, the intensity profile from the TDSE shows the multiple-ring structure, which is the general feature due to the unfavorable phase-matching,[31]and the phase along the azimuthal angle changes rapidly and its value along the radial direction is shifted from one ring to another, as shown in Figs.5(a)and 5(b).The results from the QRS show the same features in the intensity and phase distributions, see Figs.5(c) and 5(d).In the far field, multiple-ring structure is inherited in the spatial intensity profile from the TDSE,by considering the phase only with corresponding considerable intensity, the less-ring structure is present, see Figs.5(e) and 5(f).The behavior of intensity and phase results from the QRS is about the same as that from the TDSE,as shown in Figs.5(g)and 5(h).Thus,the QRS and the TDSE can reach the general agreement for simulating the macroscopic vortex HHG when the gas jet is put at the laser focus.

We then locate the center of gas jet at 2 mm before the laser focus.The spatial intensity and phase profiles of H23 from the TDSE and the QRS are shown in Fig.6.In general,both the TDSE and the QRS present the multiple-ring structure in the intensity profiles in the near and far fields, indicating the poor phase-matching of HHG by varying the macroscopic condition.[31]However, at the quantitative level, the obvious difference between the two methods can be identified in the intensity distribution,including the intensity ratio of each other in the multiple ring, the position of major ring, and the number of visible rings.Meanwhile, the phase profiles from two methods also show the significant difference no matter nearor far-field results are considered.Therefore, when the gas jet is put before the laser focus, the QRS can only attain the qualitative agreement with the TDSE.We have also checked the spatial intensity profiles of fractional harmonics in the far field and have identified that the QRS agrees with the TDSE in a qualitative manner for predicting the multiple-ring structure together with the gap structure.

4.4.Analysis of dependence of agreement between TDSE and QRS on the macroscopic condition

In the above,we have shown that the agreement between the TDSE and the QRS for simulating the vortex HHG is dependent on the macroscopic condition, i.e., the position of gas jet with respect to the laser focus.To explain this phenomenon, we perform the time-frequency analysis for the single-atom and macroscopic propagated HHG.In Fig.7, we show the time-frequency picture of single-atom HHG from the TDSE and the QRS by using the wavelet transform.[57,58]Note that the time-frequency analysis is a commonly used technique to qualitatively resolve the classical trajectory information from the calculated HHG based on quantum mechanics.Furthermore, it can also predict the relative harmonic contributions from short and long trajectories,which cannot be obtained from the classical theory.Laser peak intensity is set as 1.5×1014W/cm2.Results from two methods display the similar feature of harmonic emissions following short and long electron trajectories guided by the classical ones(black dashed lines) in Figs.7(a) and 7(b).The detailed comparison of results for H27 indicates that the QRS generally agrees with the TDSE,but relative harmonic emissions of short and long trajectories within each half optical cycle from the QRS could be different from that from the TDSE,see emission peaks labeled by S and L in Figs.7(c)and 7(d).Two methods show different relative contributions from short and long trajectories.Thus,we can expect if high harmonics are generated from the interference of these trajectories,the QRS and the TDSE would predict the different results.

In Fig.8, we present the time-frequency analysis of macroscopic HHG with the QRS when the gas jet is placed at three different positions.Clearly, the picture of harmonic emission is greatly changed by varying the position of gas jet.For example, both harmonic emissions from short and long trajectories can be seen when the gas jet is put at 2 mm before the laser focus in Fig.8(a), and lineout results for H23 show that two peaks are present in each half optical cycle in Fig.8(b).When the gas jet is put at the focus, harmonic emissions from long trajectories are dominant, as shown in Figs.8(c) and 8(d).If the gas jet is put after the laser focus,it is known that the favorable phase-matching can be achieved and harmonic emissions from short trajectories survive after macroscopic propagation, see Figs.8(e) and 8(f).The above results are consistent with the analysis of phase matching of vortex high harmonics in Ref.[31].The phase matching is due to the interplay of the geometric phase of driving laser and the intrinsic induced-dipole phase of laser-atom interaction,which is sensitive to the position of gas jet.This can also be seen in the map of spatial coherent length, which can be calculated analytically for short-and long-trajectory high harmonics,respectively,see Fig.6 in Ref.[31].We can conclude when the harmonic emissions from either short or long trajectories are dominant in the macroscopic vortex HHG,the QRS can reach a good agreement with the TDSE, like in Figs.2-5.However, if harmonic emissions from both short and long trajectories are present in the macroscopic HHG,the spatial intensity and phase profiles are resulted from their interference.As shown in the single-atom results in Fig.7,the QRS cannot accurately predict the relative harmonic emissions of two trajectories within some half optical cycles.So the QRS is not able to simulate the interference of two trajectories precisely at the quantitative level.We thus can understand that only the qualitative agreement between the QRS and the TDSE can be reached in Fig.6.

Fig.7.Time-frequency picture of single-atom HHG from the TDSE(left column) and the QRS (right column).In panels (a) and (b), harmonic energy versus emission time following the classical short(S)or long(L)trajectory is shown(black dashed lines).Emission intensity of H27(pink lines in panels (a) and (b)) as a function of time is plotted in panels (c)and(d),respectively.

Fig.8.Time-frequency analysis of macroscopic propagated HHG field at the exit of gas medium by using the QRS.Results are obtained at radial distance of 25 µm and azimuthal angle of 0.Three cases are considered when the gas jet is placed at 2 mm before (first column), at(second column),and after(third column)the laser focus.Electron classical trajectories(black dashed lines)obtained assuming laser intensity of 1.5×1014 W/cm2 are plotted in the upper row.Lower row: emission profiles of H23 indicated by pink lines in the upper row.

5.Conclusion

We simulated the generation of vortex high-order harmonic generation (HHG) driven by the Laguerre-Gaussian(LG) beam with the nonzero orbital angular momentum(OAM)by using two approaches to obtain the single-atom induced dipoles,i.e.,through the quantitative rescattering(QRS)model or solving the time-dependent Schr¨odinger equation(TDSE).We showed that the QRS can greatly improve the total HHG spectra computed by the strong-field approximation(SFA),and achieve a good agreement with the TDSE.We then compared spatial intensity and phase distributions of vortex HHG from the TDSE and the QRS in detail, including harmonic emissions in the near and far fields and harmonics with integer and fractional orders.We found that the QRS can reach perfect agreement with the TDSE when the gas jet is put after the laser focus,a reasonably good agreement can be reached between the two methods if the gas jet is placed at the laser focus,and the QRS only qualitatively agrees with the TDSE when the gas jet is located before the laser focus.We finally performed a time-frequency analysis for the single-atom and macroscopic vortex HHG.And we revealed that varying the position of the gas jet with respect to the laser focus can change the phase-matching condition,leading to harmonic emissions from short or long trajectories accumulated in the macroscopic vortex HHG differently,the existence of interference between two trajectories makes it difficult to simulate the spatial profiles of HHG accurately for the QRS.

In this work,we have carefully calibrated the QRS model for simulating the vortex HHG against the TDSE results.Note that it has been established that the QRS model can predict the HHG spectrum (including the amplitude and phase)as accurate as that from the TDSE in the single-atom response level.[40]Thus the simulated macroscopic HHG spectrum based on the QRS model is generally considered about the same as that based on the TDSE method.This is true for the HHG driven by the laser beam without the OAM.[45]However, as demonstrated in this work, this is not entirely valid when we focus on the spatial intensity profiles of vortex high harmonics.Such conclusions are unexpected and have not been addressed by others before.We have demonstrated that in the favorable phase-matching condition,the QRS can be safely used to accurately simulate the vortex HHG.Under unfavorable phase-matching conditions,the QRS can either reach the quantitative agreement with the TDSE or successfully predict the main features in the macroscopic HHG from the TDSE in a qualitative way.Thus this work ensures that the QRS can be applied to replace the TDSE in the single-atom response for simulating the vortex HHG,making the macroscopic calculation more efficient since the QRS takes much less time than the TDSE.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos.12274230, 91950102, and 11834004), the Funding of Nanjing University of Science and Technology (Grant No.TSXK2022D005), and the Postgraduate Research&Practice Innovation Program of Jiangsu Province of China(Grant No.KYCX230443).