Multi-channel generation of vortex beams with controllable polarization states and orbital angular momentum

Ziyao Lyu(吕子瑶), Pan Wang(王潘), and Changshun Wang(王长顺),†

1State Key Laboratory of Advanced Optical Communication Systems and Networks,School of Physics and Astronomy,Shanghai Jiao Tong University,Shanghai 200240,China

2School of Data Science,The Chinese University of Hong Kong,Shenzhen 518172,China

Keywords: light field modulation,holography,optical vortex,polarization

1.Introduction

In the information era, new services and applications are causing an exponential increase in aggregated data traffic, which motivates the development of innovative optical communication technologies to sustain a required massive increase in the information capacity.[1-3]In terms of the demand for continuously increasing information transmission,conventional communication systems based on wavelength and time division multiplexing, together with amplitude and phase degrees of freedom of light, are approaching a bottleneck.[2,4]Because of the development of research in the field of optics,light can provide another information dimension,namely angular momentum, to solve the problem mentioned above.Generally,propagating light waves possess two distinct forms of angular momentum.[5-8]Firstly, light can carry spin angular momentum (SAM).SAM is inherent in light beams with elliptical polarization states and depends on the field vector rotations that take place at every point of the beam crosssection.[9,10]The SAM degree of freedom of light plays a key role in optical communication systems.[11,12]For example,dual polarization in fiber optic eigenvalue communication has been reported recently in order to overcome the limitation of information transmission in conventional optical communication systems.[13]In addition to SAM,optical vortex,referring to a light beam carrying intrinsic orbital angular momentum(OAM), has attracted extensive attention in modern photonics and optics.[14-16]A vortex beam possesses helical phase front comprising an azimuthal phase term exp(ilφ), wherelrepresents the topological charge andφis the azimuthal angle.There is an isolated point singularity in the optical field of vortex light.This type of vortex is commonly known as phase vortex,characterized by the phase singularity.[17]Optical vortex light is one of the special beams with a complex beam shape linked to the space physical dimension of light waves.Recently,structured light has been widely explored in optical communication systems to facilitate the substantial increase of transmission capacity and efficient usage of limited frequency resources.[17-19]

In order to further improve the data capacity of angularmomentum-enabled communication systems, the simultaneous formation of multiple optical SAM and OAM modes using a single element with a single-input beam is highly desired.[20]A considerable amount of attention has been directed to the multi-channel generation of polarized optical vortices carrying both SAM and OAM with a single Gaussian beam for adding additional degrees of freedom to optical communication systems, which is greatly helpful to realize tremendous promotion of the information capacity.[21]Therefore,research on polarized optical multi-vortices generators becomes a critical step for the development of multidimensional multiplexing technologies and high-capacity communication.Generally,for vortex beam based optical communications, OAM multiplexing and OAM coding/decoding are two important ways to carry and deliver data information.For OAM multiplexing, multiple collinear vortex beams are used to carry data information, which is known as a subset of the mode division multiplexing technique.[22]In addition,the vortex beams carrying OAM can also be regarded as symbols to realize data coding/decoding transmission.In theory,the OAM states are theoretically infinite, making it feasible to realize highdimensional coding/decoding for data transfer in both traditional and quantum communications.[23]Particularly, diffractive phase gratings are commonly applied for OAM mode generation and coding/decoding.In 2021, a novel design technique for multi-dimensional OAM coding/decoding has been proposed based on a two-dimensional vortex holographic grating.[24]Moreover, optical vortex beams control based on phase fork gratings has also been realized for optical connectors and information transmission.[25]

However, the works mentioned above mainly focus on optical OAM modes,while the polarization degree of freedom of light cannot be controlled.Moreover, generating multiple light beams with desired amount of optical angular momentum is usually achieved with a series of individual bulky polarization and spatial phase devices, which sharply decreases the configurability of communication systems.[26]In addition,the wavelength of the incident light and generated vortex light is usually strictly limited.The demands of shrinking,broadband and multi-output optical devices call for new approaches.In this regard, recently developed optical components have also been applied to generate optical vortices.[27]Nevertheless, in many cases,the wavelength and polarization of the generated vortex light are restricted, and the use of these optical components as practical devices is often limited by their manufacturing complicity, inflexible SAM adjustability and wavelength sensitivity, which hinders the development of highcapacity communication systems.In recent years, great progresses have been made.For example, Wanget al.proposed combined phase-only holograms to produce sophisticated perfect optical vortex arrays and the contributed scheme enabled dynamically controllable multi-ring, topological charges, eccentricity, size, and the number of optical vortices.[28]Shanget al.proposed an integrated phase-only scheme to generate multiple multiplexed vortex beams simultaneously, constituting a multiplexed vortex state array, where the spatial position, as well as the corresponding orbital angular momentum spectrum, could be manipulated flexibly as desired.[29]Fuet al.demonstrated an approach experimentally to acquire multiple beams on a hybrid Poincare sphere,and the state in each diffraction order was controllable.[30]Besides,orbital angular momentum comb generation,consisting of a series of discrete,equally spaced,and equally weighted orbital angular momentum modes,has also been demonstrated both theoretically and experimentally through azimuthal binary phases.[31]

In this work,we have designed a polarized optical multivortices generator based on the analysis of Stokes-Mueller formalism and cross-phase modulation.Theoretical discussion shows that multi-output vortex beams with tunable polarization states and OAM can be generated simultaneously through a single-input linearly polarized Gaussian beam.To verify our scheme, the designed multi-vortices generator has also been recorded in an azobenzene liquid-crystalline film experimentally.Four OAM-carrying light beams with anticipated topological charges and actively controllable polarization states are obtained,and there is a good agreement between the theoretical analysis and experimental results.

2.Principle

Two pairs of recording beams with different wavelengths are required for one-step holographic recording of the designed polarized optical multi-vortices generator in an azobenzene liquid-crystalline film.Firstly,we consider two coherent monochromatic electromagnetic plane waves with the wavelength ofλ.The holographic interference field isE(r,t)=E1(r,t)+E2(r,t),in which

wherek=2π/λis the wave vector,ωis the angular frequency,θis the angle betweenkandz-axis,χ1andχ2are two controllable additional phases.The intersection angle between the polarization direction of light and thexzplane isα.ϕ1andϕ2represent the phase differences between they-axis component and the in-planexzcomponent forE1(r,t) andE2(r,t), respectively.The Stokes vector of the holographic fieldE(r,t)is expressed as

in which〈〉 is for time average,S0represents the total light intensity andS1-S3are the intensities related to the components of interference light that are linearly polarized alongxy, linearly polarized in the directions of±45◦, and circularly polarized,respectively.[32]

Then, the Mueller matrix of the photoinduced liquidcrystalline structure formed by one-step holographic recording is calculated based on the Stokes vector.LetMdenote a nondepolarizing Mueller matrix and there exists a diattenuatorMDand retarderMRpair such thatM=MRMD.[33]Specific Mueller matrix decomposition into two elementary matrices can be described by

wheredis the thickness of the material,s1=S1/S0is the normalized Stokes parameter,γxandγyare the attenuation coefficients alongxandydirections, respectively,γ0=(γx+γy)/2 andI(s1)∆γ=γy-γxwithI(s1)representing a parameter related tos1because the anisotropic response of the liquidcrystalline film is proportional to light intensity.The form ofI(s1) is determined by the effect of cross-phase modulation discussed below.The diattenuation Jones matrixJxycan be converted to a Mueller matrixMxythrough the transformation

withm11being the element ofMxyand⊗indicating direct product.[34]According to Eqs.(4) and (5), the diattenuation vector inx-ydirections isDxy= (tanh[kI(s1)∆γd] 0 0)T.Similarly, the Jones matrices of the linear diattenuatorJ±45oriented in the directions of±45◦and the circular diattenuatorJLR are

in whichγ0=(γ45+γ-45)/2 forJ±45andγ0=(γL+γR)/2 forJLRwithγ45,γ-45,γL,γRbeing the attenuation coefficients related to the light with±45◦linear polarization and leftand right-handed circular polarization, respectively.Based on Eq.(5), the diattenuation vectors ofM±45andMLRare calculated asD±45= (0 tanh[kI(s2)∆γd] 0)TandDLR=(0 0 tanh[kI(s3)∆γd])T,respectively.Therefore,the diattenuation vectorDDofMDis related to the Stokes vector and determined by

Fig.1.(a) Experimental setup for the one-step holographic recording of the proposed polarized optical multi-vortices generator in a liquidcrystalline film. θ1 and θ2 are the incident angles of the resonant pump light and off-resonant pump light,respectively. α1,α2,β1 and β2 are the intersection angles between x-z plane and the polarization directions of four recording beams.(b)Poincar´e sphere is defined in a space spanned by normalized Stokes parameters, representing the degrees of linear polarization (s1), diagonal polarization (s2) and circular polarization (s3),respectively.A vector from the origin to a point (ψ, ε) on the sphere surface defines a Stokes vector and indicates optical SAM.

To record the proposed polarized optical multi-vortices generator,an optical amplitude pattern and a polarization pattern should both be formed within the dual-color holographic recording field.Firstly, the Mueller matrix of the liquidcrystalline structure induced by the polarization pattern is discussed.In this case,two off-resonant recording beams are required to be orthogonally polarized,and thus the polarization state within the interference light field is modulated periodically in space.For simplification, the polarization directions of the two recording beams are set alongx- andy-axes, respectively.Under the assumption of paraxial approximation,the Stokes vector of the off-resonant holographic optical field is expressed as

with ∆χr=χ1-χ2.According to Eqs.(7) and (8), the diattenuation submatrixmDis

On the other hand, the photoinduced birefringence in the liquid-crystalline film is also related to the corresponding Stokes parameters.The effect of a retarder upon polarization states is equivalent to a rotation on the Poincar´e sphere in Fig.1(b) and the retardance submatrixmRcan be written as[35]

whereRr=kr∆ndis the retardance with ∆nbeing the anisotropic birefringence constant,andεijkis the Levi-Civita permutation symbol (i,j=1, 2, 3).Therefore, the Mueller matrix of the liquid-crystalline structure recorded by the optical polarization pattern is obtained throughMr=MrRMrD.

Then, the Mueller matrix of the liquid-crystalline structure generated by the optical amplitude pattern is calculated.Under this situation, the light intensity varies periodically in space and the Stokes vector of the interference light field of two resonant beams,G1andG2,is

In this case,only linear birefringence as well as linear diattenuation exist.The Mueller matrix related to the optical amplitude pattern isMg=MgRMgD.

Here, the mechanism of cross-phase modulation is discussed in order to store the optical patterns in the liquidcrystalline film and generate structures described by the coupling ofMgandMr.In terms of the photosensitive material in this work, the liquid crystals can exist in two isomeric states: trans and cis.The transition between the two states happens under the illumination of light and thermal influence.At room temperature, trans-isomers are more stable than cis-isomers.As shown in Fig.2(a), most of the absorption bands of trans-isomers lie in the blue-green region of shorter wavelengths.As the activation of shortwavelength resonant pump light transforms the liquid crystals from trans-to cis-isomers,a photoinduced periodic refractiveindex structure described byMg,corresponding to the amplitude pattern of the holographic optical field, is formed in the liquid-crystalline film because of the population change of cisisomers in space.Moreover,the photoinduced trans-to-cis isomerization further causes spectral redshift of the material, as demonstrated in Fig.2(a), and the absorption of off-resonant light with longer wavelength leads to photoexcited cis-to-trans back isomerization.[36]During the photoinduced isomerizations, the reorientation direction of photoaligned liquid crystals is forced to become perpendicular to the spatially distributed polarization direction of recording light.The transcis-trans isomerization processes are illustrated in Fig.2(b),whereσAandσBrepresent the absorption cross sections of trans- and cis-isomers,ϕAandϕBrepresent the quantum yields of photoinduced isomerizations from trans to cis and from cis to trans, respectively.KTis the process of thermal cis-trans isomerization.Cross-phase modulation induced by photoinduced isomerizations causes spectral changes in longwavelength light through the modulation of short-wavelength light.This effect is described by the coupled waves propagation equation[37]

withnrandνrbeing the nonlinear refraction and absorption coefficients in terms of the off-resonant light, respectively.During this process,the isomerization rate equation related to the population of trans-(NA)and cis-isomers(NB)is

whereRi=σiϕiIi/(hνi) (i=A, B) are the rates of trans-cis and photoexcited cis-trans isomerizations.RTis a constant representing the rate ofKT.The time-dependent population changes of trans- and cis-isomers induced by the effect of cross-phase modulation are

withN0being the total number of isomers within the holographic recording area.Based on the optical polarization pattern and photoexcited cis-to-trans isomerization, the photoinduced molecular reorientation of trans-isomers is controlled by spatially rotating optical-axis directions of the longwavelength interference light, and thus the reorientation angles of liquid crystals vary periodically from 0 to 2πalongx-axis, resulting in the formation of a periodic birefringence structure, defined by the polarization dependence of refractive indices, in the film described byMr.After reaching a stable state, the photoinduced anisotropy in the material is proportional to the population of photoexcited trans- and cis-isomers, and thusI(si) in Eq.(7) can be expressed asgASgi/(gASg0+gBSr0+1)forMgandgBSri/(gASg0+gBSr0+1)forMrwithgq=σqϕq/(hνqRT) (q= A, B) according to Eq.(14).Through this dual-color modulation transfer method,the designed polarized optical multi-vortices generator can be recorded in the liquid-crystalline film.

Finally,the complete Mueller matrix of the designed alloptically tunable polarized optical multi-vortices generator is the coupling ofMgandMr,expressed as

withR(ξ)being the 4×4 rotation matrix alongz-axis.Considering a single-input linearly polarized Gaussian light, simultaneous formation of multi-output optical SAM and OAM modes are calculated throughsn(ψn,εn)=M(ξ)si(ψi)withsiandsnbeing the normalized Stokes vectors of the incident andnth-order diffraction light,respectively.The results of theoretical analysis on spin and spatial degrees of freedom of the generated optical vortices are presented in Fig.3.Through the series expansion ofM(ξ),sncontains the exponential term exp(inlφ), and thus the topological charges of OAM modes equalnl.The output SAM modes are related tos3that is the function ofεncontrolled byξ.In terms of the spatial degree of freedom of the diffraction beams, we control the azimuthdependent phases ∆χrand ∆χgas ∆χr=∆χg=lφ,and thus the OAM of the generated vortex beams can be controlled through recording light fields.During this process,the recorded polarized optical multi-vortices generator can be erased through the heating method (∼60◦C) and another generator with different values oflcan be recorded in the same liquid-crystalline film at the same point.This writing-erasing-writing cycle can be repeated rapidly over a hundred times without fatigue.On the other hand, manipulation of spin degree of freedom is independent of the spatial degree of freedom.The SAMcarrying optical vortices can be modulated continuously from left-handed to right-handed elliptically polarized with various ellipticityεthrough manipulating the rotation angleξof the polarized optical multi-vortices generator(described by the rotation matrix in Eq.(15)),and the modulation depth of SAM,defined as|LSAM/LmaxSAM|withLmaxSAMbeing the maximum magnitude of SAM carried by polarized light, is actively controllable between 0% and 100%.Moreover, the wavelength of the incident light is not fixed and multi-channel generation of vortex beams carrying tunable SAM and OAM is expected to be broadband because the Mueller matrices in Eq.(15)are not related to the wavelength of input light.

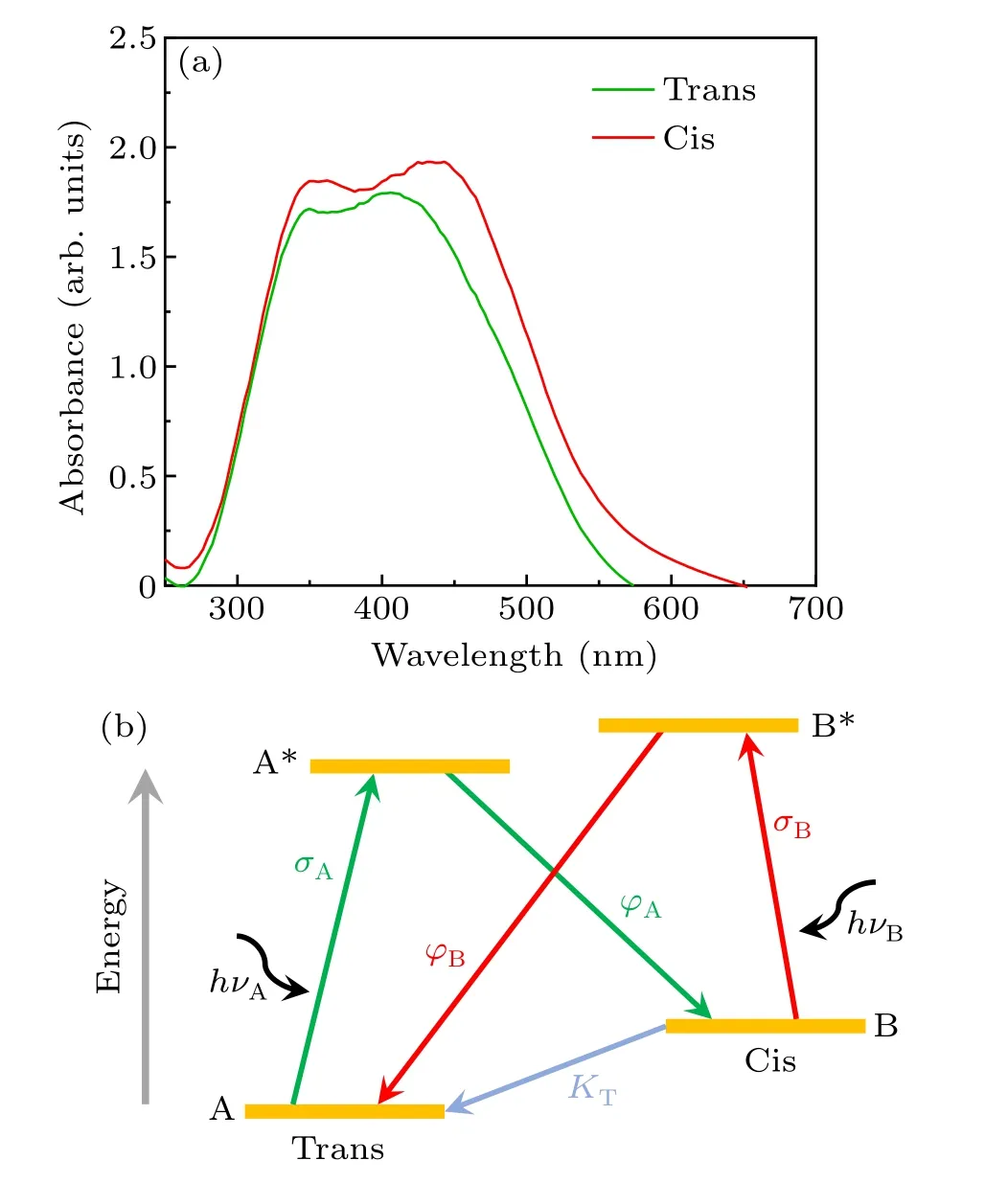
Fig.2.(a) Absorption spectra of trans- and cis-isomers of the photosensitive liquid crystals.(b)Schematic energy-state conversion between the two isomers.σA-ϕA represents photoinduced trans-to-cis conversion,σB-ϕB shows photoexcited cis-to-trans back isomerization and KT is the spontaneous thermal induced process.

Fig.3.Multi-channel generation of vortex beams with controllable polarization states and topological charges based on the theoretical analysis of Muller matrices.

In the following section, the designed polarized optical multi-vortices generator is demonstrated experimentally to verify our scheme, and a group of vortex beams with desired topological charges of 3nand actively controllable polarization states are generated.

3.Experimental setup

The experimental setup for multi-channel generation of polarized vortex beams is presented in Fig.1(a).Two 532 nm beams from a Nd:YAG laser with the same power density of 150 mW/cm2are selected as resonant recording light whose wavelength is located in the absorption spectrum of the sample(thickness∼1 µm), as shown in Fig.2(a).The selected resonant laser wavelength plays two roles in this work.Firstly,it effectively leads to photoinduced structures in the liquidcrystalline film; secondly, it is relatively weakly absorbed by the sample, which promotes uniform distribution of light intensity across the whole sample.The two resonant recording beams interfere at the surface of the sample at an angle of 3◦(2θ1=3◦).On the other hand, two 633 nm beams from a He-Ne laser with an equal power density of 180 mW/cm2are selected as off-resonant recording light.The intersection angle of the two red beams at the surface of the sample is 5◦(2θ2=5◦).The sample in our experiment is a supermolecule material by ionic self-assembly of poly (ionic liquid) (PIL)and azobenzene dye.The charged polymer poly (1-butylvinylpyridinium bromide) PIL is selected as the main chain segment, and the methyl orange (MO) dye is selected as the building unit due to its capability for photo-induced isomerization.For the preparation of ionic self-assembly complex,a 2 mg/ml PIL aqueous solution is added dropwise to a MO aqueous solution with the same concentration, i.e., in a 1:1 molar charge ratio.The precipitated complex is filtrated and washed several times with doubly distilled water to remove residual salts and possible non-complexed precursors, then dried in vacuum at 60◦C for 12 h.Vertically linearly polarized Gaussian light with the wavelength of 650 nm is selected as the probe light to investigate the properties of the recorded polarized optical multi-vortices generator.The polarization states and intensity distributions of the output light waves are detected with a polarimeter (THORLABS, PAX5710VIS-T)and a CCD(CINOGY,CinCam-1201),respectively.Based on the directly measured polarization states and interference patterns,the amount of SAM and OAM carried by the generated polarized vortex beams can be evaluated experimentally.All measurements are performed at room temperature.According to the photo-alignment principle of liquid crystals discussed in the previous section, the designed polarized optical multivortices generator in Fig.4 is formed in the sample through one-step holographic recording.

Fig.4.Schematic illustration of multi-channel generation of SAMcarrying vortex beams with desired topological charges of 3n and alloptically controllable SAM.Pin and Pdif represent the polarization states of the incident light and diffraction light,respectively.

Fig.5.The experimentally captured image of diffraction light.Simulated helical phase patterns of the (a1) +first-order, (b1) -first-order,(c1)+second-order and(d1)-second-order structured diffraction beams.(a2)-(d2)Experimentally measured donut-shaped intensity profiles of the four generated OAM-carrying beams imaged on the CCD corresponding to (a1)-(d1).According to the simulated holograms of the interference of Gaussian light and structured light with helical phases presented in(a1)-(d1),the topological charges of the±first-order and±second-order diffraction beams are measured to be±3 and±6,respectively.

4.Results and discussion

Firstly, in terms of the spatial degree of freedom, the topological charges of the generated OAM-carrying beams are measured experimentally.According to theoretical analysis,the topological charge of diffraction lightmsatisfies the equationm=nl+l0withnbeing the diffraction order,landl0being the topological charges of recording holographic light field and incident light, respectively,[38-40]here,l=3.As shown in Figs.5(a2)-5(d2), four diffraction beams display donutshaped light-intensity profiles with phase singularities at the center of each light spot, characteristic of optical vortices.A coherent Gaussian beam is applied to investigate the OAM of the first-order and second-order vortex diffraction lights based on the interference patterns.The difference between the number of interference fringes in the upper-half part and the lowerhalf part of the interference pattern is equal to the topological charge.The experimental results are consistent with the theoretical analysis and the simultaneous generation of a group of vortex beams with anticipated topological charges of 3nhas been realized experimentally.

Fig.6.All-optical SAM control of the (a) +first-order, (b) -first-order, (c) +second-order and (d) -second-order OAM-carrying diffraction beams has been demonstrated experimentally on the normalized Poincar´e sphere.When the incident light keeps vertically linearly polarized,the generated vortex beams can be manipulated from left-handed to right-handed elliptically polarized with tunable ellipticities in the ranges from-34.938◦to 36.765◦for the first diffraction order and from-35.724◦to 38.208◦for the second diffraction order.The polarization directions of the four vortex beams all can be modulated continuously between-90◦and 90◦.

Then, the polarization states of the generated vortex beams can be controlled by rotating the recorded optical element and the results are presented on the Poincar´e sphere with red dots in Fig.6.For the±first diffraction orders (see Figs.6(a)and 6(b)), the polarization direction of light can be manipulated to change in the total range from-90◦to 90◦as the red dots in Figs.6(a3) and 6(b3) make one revolution around the center of the Poincar´e sphere ins1-s2plane.[41]According to Figs.6(a2) and 6(b2), the red dot shifts between the north and south poles ofs3-axis, which indicates that the first-order vortex diffraction light can be controlled to both left- and right-handed elliptically polarized with wideranging tunable ellipticities.The maximum magnitude of ellipticity measured in the experiment is 36.765◦.Similarly,the polarization directions of the±second-order vortex diffraction beams are also controlled randomly between-90◦and 90◦, as shown in Figs.6(c) and 6(d).Moreover, the ellipticity of the polarization state can be manipulated continuously from-35.724◦to 38.208◦when the incident light is fixed to be linearly polarized in the vertical direction.According to Fig.1(b), the SAM of polarized light is determined by two parameters, ellipticityεand phase itemψ.As the recorded polarized optical multi-vortices generator is rotated, alternate SAM modulation from left-handed to right-handed with the wide-ranging tunable magnitude is realized for all diffraction beams.For the vortex beams with topological charges of±3 in Figs.6(a) and 6(b), the vortex light is regulated from linearly polarized with|ψ|=0.5πto left-handed elliptically polarized with the maximum SAM of-0.960/ω;then,the ellipticity decreases gradually and the vortex light returns to linearly polarized;afterwards,the handedness of SAM is reversed and the magnitude of right-handed SAM increases again to reach the peak of 0.945/ω; finally, the right-handed elliptically polarized vortex light is modulated to linearly polarized with|ψ|=0.5π.During this process, the generated maximum SAM of the first-order diffraction light equals 0.960Land the manipulation range of SAM modulation depth is continuous from 0 to 96.0%.On the other hand, in terms of the second-order vortex diffraction beams with topological charges of±6 in Figs.6(c)and 6(d),a similar SAM manipulation process can also be achieved.The handedness of SAM is switchable from left-handed to right-handed and the maximum modulation depth of SAM is measured up to 97.2%.

5.Conclusion

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant No.92050116).