Ultralow-temperature heat transport study of noncentrosymmetric superconductor CaPtAs

Yimin Wan(万一民), Erjian Cheng(程二建), Yuxin Chen(陈宇鑫), Chengcheng Zhao(赵成成),Chengpeng Tu(涂成鹏), Dongzhe Dai(戴东喆), Xiaofan Yang(杨小帆), Lu Xin(辛路),Wu Xie(谢武), Huiqiu Yuan(袁辉球),4,‡, and Shiyan Li(李世燕),4,5,§

1State Key Laboratory of Surface Physics and Department of Physics,Fudan University,Shanghai 200438,China

2Leibniz Institute for Solid State and Materials Research(IFW-Dresden),01069 Dresden,Germany

3Center for Correlated Matter and School of Physics,Zhejiang University,Hangzhou 310058,China

4Collaborative Innovation Center of Advanced Microstructures,Nanjing 210093,China

5Shanghai Research Center for Quantum Sciences,Shanghai 201315,China

Keywords: noncentrosymmetric superconductor,thermal conductivity,superconducting gap structure

1.Introduction

Finding exotic superconductors and elucidating their superconducting pairing mechanism are important topics in condensed matter physics.[1]The noncentrosymmetric superconductors (NCSs) have attracted much attention since the discovery of unconventional superconductivity in CePt3Si.[2,3]The existence of antisymmetric spin-orbit coupling (ASOC) leads to spin-split electron bands, which allows for the admixture of spin-singlet (s-wave) and spin-triplet (p-wave) pairing state.[4,5]Due to the strong electron correlation effect in this f-electron NCS, it is hard to study the role of ASOC in the superconducting state alone.Subsequently, many non-f-electron NCSs with weakly correlated electrons have been found, such as Li2(Pd1-xPtx)3B,[4,5]LaPt3Si and BaPt3Si.[6,7]Therefore,it is possible to disentangle ASOC from the correlation effects.[4,5,8]However, most weakly correlated NCSs exhibit the dominant s-wave superconducting state,[9-11]which raises the question of the exact role of ASOC in the superconducting pairing state.

Recently, a new NCS CaPtAs with weakly correlated effect has attracted considerable attention.[12]It has a transition temperatureTc≈1.5 K.Specific heat and muonspin relaxation (µSR) measurements suggest nodes in the superconducting gap and broken time-reversal symmetry(TRS) in its superconducting state.[13]This has stimulated more theoretical works on CaPtAs, including spontaneous spin polarization, the origin of the gap nodes, and possible topological superconductivity.[14-16]However, more recent nuclear quadrupole resonance (NQR) measurements indicate that CaPtAs is a multigap superconductor with a large s-wave component.[17]In this context,more techniques are needed to clarify the superconducting state of CaPtAs.

Ultralow-temperature thermal conductivity is an established bulk technique to study the superconducting gap structure.[18]In this paper, we present ultralowtemperature thermal conductivity measurements on CaPtAs single crystal to investigate its superconducting gap structure.In zero magnetic field, a negligible residual linear termκ0/Tis observed, indicating a dominant s-wave pairing in its superconducting state.In magnetic fields, the field dependence ofκ0/Tsuggests CaPtAs has multiple superconducting gaps.These results are consistent with the NQR measurements in Ref.[17].

2.Materials and methods

CaPtAs single crystals were synthesized using a selfflux method.[12]The obtained single crystals have black metallic luster with mirror-like surfaces, as shown in the inset of Fig.1(a).X-ray diffraction (XRD) measurement was performed with a D8 Advance x-ray diffractometer from Bruke.The sample for transport measurements was cut into a rectangular shape of 1.10×0.15 mm2with a thickness of 0.11 mm.Four silver leads were attached to the sample surface with silver paint, which were used for both resistivity and thermal conductivity measurements.The contact resistance is about 30 mΩ at 2 K.The in-plane resistivity was measured in a physical property measurement(PPMS,Quanutm Design)in a3He cryostat.The in-plane thermal conductivity was measured in a dilution refrigerator by using a standard four-wire steadystate method with two RuO2chip thermometers,calibratedin situagainst a reference RuO2thermometer.Heat current was in theabplane, and the magnetic field was applied along thecaxis for all measurements.To ensure a homogeneous field distribution in the sample,all fields for resistivity and thermal conductivity measurements were applied aboveTc.

Fig.1.(a) Room-temperature XRD pattern from the largest natural surface of CaPtAs single crystal.The left inset shows the chematic crystal structure for the orthorhombic GaPtAs (Ca: green; Pt: orange;As:blue)with space group I41md(No.109).The top inset is the optical image of CaPtAs single crystal with four electrodes and the rocking curve of the (0012) Bragg peak.(b) The temperature dependence of resistivity at zero magnetic field for CaPtAs single crystal,with current in(00l)plane.The red line is the fit of the normal-state resistivity to the Fermi-liquid behavior ρ(T)=ρ0+AT2 from 1.5 K to 50 K.Inset: The resistive superconducting transition at low temperature.

3.Results and discussion

CaPtAs crystallizes in an orthorhombic structure with the space groupI41md(No.109).[12,13]The large natural surface is identified to be the (00l) plane by XRD measurement, as illustrated in Fig.1(a).The right inset of Fig.1(a) shows the x-ray rocking curve of the(0012)Bragg peak.The full width at half-maximum (FWHM) is only about 0.045◦, indicating the high quality of our CaPtAs single crystals.The in-plane resistivity of CaPtAs in zero field is plotted in Fig.1(b).At low temperature, the width of the resistive superconducting transition(10%-90%)is 0.09 K,and theTcis 1.36 K,defined at the 50% drop of the resistivity (T50%c ).The fit of the normal-state resistivity between 1.5 K and 50 K to Fermiliquid behaviorρ(T) =ρ0+AT2yieldsρ0= 10.5 µΩ·cm andA=2.6×10-3µΩ·cm·K-2.The residual resistivity ratioRRR=ρ(300 K)/ρ0is around 6.

Figure 2(a) shows the low-temperature resistivity of the CaPtAs single crystal in various magnetic fields up to 0.25 T.With increasing field, the superconducting transition is gradually suppressed to lower temperatures.To determine the upper critical fieldµ0Hc2(0), theTcs at different fields are plotted in Fig.2(b).An apparently linear temperature dependence ofµ0Hc2can be seen.With a linear fit of the data,µ0H10%c2(0)≈0.076 T is roughly estimated,which is taken as the bulk upper critical field.Such a linear temperature dependence ofHc2has been previously observed in other superconductors, such as MgB2,[19-21]UBe13,[22]YPtBi,[23]and pressurized Bi2Se3and Cd3As2.For MgB2, it may come from a two-band Fermi surface topology.[19-21]For heavy-fermion superconductor UBe13and non-centrosymmetric superconductor YPtBi, it was considered as an indication of unconventional state.[22,23]While for pressurized topological insulator Bi2Se3and Dirac semimetal Cd3As2, it probably relates to their topological bands.[24,25]Since density function theory calculations show that there are complex multiple electronic bands in CaPtAs[12]and CaPtAs is a non-centrosymmetric superconductor, the origin of its linear temperature dependence ofµ0Hc2needs further investigation.

Figure 3 depicts the in-plane thermal conductivity of the CaPtAs single crystal in various magnetic fields.The measured thermal conductivity contains two contributions,κ=κe+κp, which comes from electrons and phonons,respectively.In order to separate the two contributions, all the curves below 0.5 K are fitted toκ/T=a+bTα-1.[26,27]aTandbTαrepresent the contributions from electrons and phonons, respectively.The residual linear termκ0/T ≡ais obtained by extrapolatingκ/TtoT=0 K.Due to the specular reflections of phonons at the sample surface, the powerαin the second term is typically between 2 and 3.[26,27]In zero field, the fitting givesκ0/T= 0.005±0.03 mW·K-2·cm-1andα= 2.85±0.09.To show the data more clearly,κ/Tvs.T1.85is plotted in Fig.3(a).In consideration of our experimental error bar±5 µW·K-2·cm-1, theκ0/Tof CaPtAs in zero field is negligible.For s-wave nodeless superconductors, there are no fermionic quasiparticles to conduct heat asT →0, since all electrons participate in the formation of Cooper pairs.[18,26]Therefore, there is no residual linear term, as seen in V3Si and NbSe2.[26,28]However, for nodal superconductors, a substantialκ0/Tin zero field contributed by the nodal quasiparticles has been found.[18]For example,κ0/Tof the overdoped (Tc=15 K) d-wave cuprate superconductor Tl2Ba2CuO6+δ(Tl-2201) is 1.41 mW·K-2·cm-1.[29]Therefore, the negligibleκ0/Tobserved in CaPtAs indicates a dominant s-wave pairing in its superconducting state.

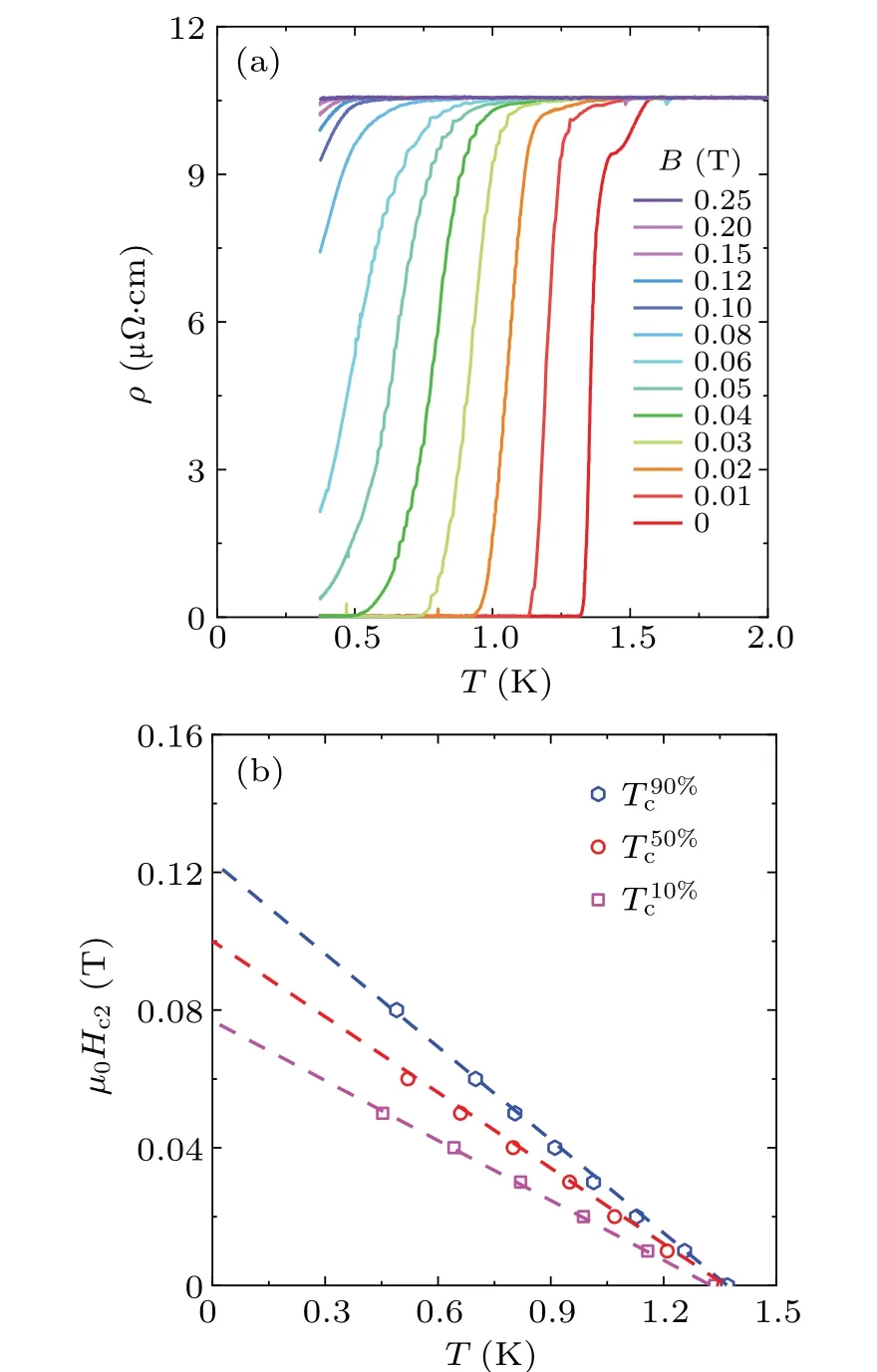
Fig.2.(a) Low-temperature resistivity of CaPtAs single crystal in magnetic field up to 0.25 T.(b) Temperature dependence of the upper critical field µ0Hc2(T), the upper critical fields were defined by dropping to 90%, 50%, 10% normal-state resistivity, respectively.The magnetic fields were applied along the c axis.The dashed lines are the linear fit to the data, which point to µ0H90%c2 (0) = 0.124 T,µ0H50%c2 (0)=0.1 T,andµ0H10%c2 (0)=0.076 T.

The field dependence ofκ0/Tcan provide further information on the superconducting gap structure.[18]The data in the magnetic fieldsH=0.01 T,0.02 T and 0.03 T are also fitted, as seen in Fig.3(b).Above 0.03 T, the data become more and more noisy, which are not shown.The normalizedκ0(H)/Tas a function ofH/Hc2(µ0Hc2= 0.076 T) for CaPtAs is plotted in Fig.4.For comparison, similar data of the clean s-wave superconductor Nb,[30]the dirty s-wave superconductor ally InBi,[31]the multiband s-wave superconductor NbSe2,[28]and an overdoped d-wave cuprate superconductor Tl-2201[29]are also plotted.For single-band s-wave superconductor Nb, theκ0(H)/Tchanges not much even up to 40%Hc2,[30]while for nodal superconductor Tl-2201,a small field can yield a quick growth in the quasiparticle density of state (DOS) due to the Volovik effect, and the low-fieldκ0(H)/Tshows a roughly√Hdependence.[29]In the case of NbSe2, the distinctκ0(H)/Tbehavior was well explained by multiple superconducting gaps with different magnitudes.[28]

Fig.3.The in-plane thermal conductivity of CaPtAs single crystal (a)in zero field, and (b) in magnetic field applied along the c axis.The solid lines represent the fits to κ/T =a+bTα-1 for the data in various magnetic fields.

Fig.4.Normalized residual linear term κ0/T of CaPtAs as a function of H/Hc2, with bulk µ0Hc2 = 0.076 T.For comparison, similar data are shown for the clean s-wave superconductor Nb,[30] the dirty swave superconductor alloy InBi,[31] the multiband s-wave superconductor NbSe2,[28] and an overdoped d-wave cuprate superconductor TI-2201.[29]

From Fig.4, the field dependence ofκ0(H)/Tfor CaPtAs grows slightly lower than that of the multiband s-wave superconductor NbSe2and faster than that of the dirty s-wave superconductor InBi.We check two possible scenarios for such a field dependence ofκ0(H)/T.One is that CaPtAs is an s-wave superconductor in the‘dirty’limit.To check whether CaPtAs is in the dirty limit, we estimate its superconducting coherence lengthξ0.Fromµ0Hc2(0)=0.1 T,we obtainξ0≈42 nm through the relationHc2(0)=φ0/(2πξ20).Recently,magnetic penetration depth measurements found an electron mean free pathl ≈1.5 nm in CaPtAs.[13]l ≪ξ0indicates that CaPtAs is indeed in the‘dirty’limit.The other scenario is that CaPtAs is a multiband superconductor.Indeed,the electronic structure calculations of CaPtAs show multiple complex bands.[12]Therefore, the field dependence ofκ0(H)/Tin CaPtAs may result from both its dirtiness and multiple gaps.

For noncentrosymmetric superconductors, broken inversion symmetry and the accompanying antisymmetric spin-orbit coupling admix spin-singlet and spin-triplet pairing.[4]The typical examples are Li2Pd3B and Li2Pt3B.[4]The triplet contribution is weak in Li2Pd3B, leading to a wholly open but anisotropic gap.[4]However,the significantly larger spin-orbit coupling in Li2Pt3B allows the spin-triplet component to be larger in Li2Pt3B,producing line nodes in the energy gap.[4]Here for noncentrosymmetric superconductor CaPtAs, while the µSR measurements suggest nodes in the superconducting gap,[13]the latest NQR measurements[17]and our current ultralow-temperature thermal conductivity measurements indicate multiple superconducting gaps with a dominant s-wave component.In this sense, the spin-triplet component in CaPtAs may not be as large as that in Li2Pt3B.

4.Conclusion

In summary,we have measured the ultralow-temperature thermal conductivity of CaPtAs single crystal.The negligible residual linear termκ0/Tin zero field and the field dependence ofκ0/Tsuggest that CaPtAs has multiple superconducting gaps with a dominant s-wave component.These results are consistent with previous NQR measurements.More experimental and theoretical studies are desired to clarify the exact superconducting gap structure of this noncentrosymmetric superconductor.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No.12174064), the National Key R&D Program of China (Grant No.2022YFA1402200),and the Shanghai Municipal Science and Technology Major Project(Grant No.2019SHZDZX01).