基于有限元仿真的不同胸型胸围截面压力位移变化研究
2023-12-15刘宿慧顾明月潘怡婷邹奉元
刘宿慧, 顾明月, 潘怡婷, 邹奉元,b,c
(浙江理工大学 a.服装学院; b.丝绸文化传承与产品设计数字化技术文化和旅游部重点实验室; c.浙江省服装工程技术研究中心,杭州 310018)
人体在受到外界压力后会发生形变,形变程度是反映压力舒适性的重要指标[1]。因此,探究压力与体表形变的规律对压力舒适性影响具有重要意义。近年来,许多学者利用有限元数值模拟对服装压力与相应位移之间的关系进行研究。Sun等[2-3]利用逆问题的迭代求解方法预测了乳房超弹材料系数,基于该系数建立了人体生物力学有限元(FE)模型,分析文胸对乳房皮肤的压力分布。Wang等[4]以跑步紧身裤为研究对象,分析了腿部骨骼、肌肉、皮肤、服装面料与体表位移之间的关系,预测了穿着过程中紧身裤对小腿肌肉位移的影响。王燕珍等[5]通过对人体皮肤的动态测量,研究穿着紧身裤时服装织物弹性与皮肤变形之间的相关性。Liu等[6]建立标准女体有限元模型,研究了服装压力对胸部的影响及服装胸围应变与织物杨氏模量间的关系。以上研究主要针对单一体型或归一化人体进行研究,没有考虑体型差异造成的压力与位移变化。因此,本文结合胸型形态差异,利用有限元方法对不同胸型的压力位移变化规律进行研究。
由于胸型差异的影响,女体胸围截面各部受压状态及形态变化有所不同,不同体型的人体受到外力时会呈现不同变化规律[7]。因此,用有限元仿真得出体表形态变化规律时,需将胸型差异考虑在内。常丽霞等[8]基于乳深、乳平围两个特征变量对女性乳房的立体程度进行表征,将乳房形态细分为9类。Liu等[9]通过对人体108个测量项目进行主成分分析,筛选出乳房深和胸宽厚比两个指标,对乳房形态进行分类。Shi等[10]分析年龄和BMI对胸罩尺码系统的影响,提出将年龄和BMI作为胸型分类的辅助标准。探究不同胸型下女体受法向压力与体表内向位移之间的关系,对于压力舒适性研究具有实际和应用价值。
综上,本文为获取不同胸型的人体数据,采用三维扫描仪测量女体躯干数据,提取重建坐标系下的乳房参数,根据乳房深与乳房宽比值对胸型进行分类,构建不同胸型的有限元接触模型,模拟不同胸型在不同受压状态下的形态变化,探究不同胸型的压力—位移变化规律,建立胸围截面处的压力、位移和角度间函数关系,以期为紧身服装压力舒适性研究提供参考。
1 胸围截面几何模型构建
本文通过三维扫描仪获取女体表面的空间信息,利用逆向工程软件对三维数据进行预处理并与内层结构数据装配,分胸型生成人体胸部的几何模型,为后续分类建立有限元模型提供数据支撑。
1.1 数据获取
为获取各种胸型的体表形态数据,本文利用美国[TC]2NX-16三维扫描仪获取了136名年龄在18~25岁女性受试者的点云数据。实验环境温度控制在20 ℃左右,相对湿度控制在60%左右,实验对象保持上半身全裸,下半身穿着贴体浅色内裤的状态[11]。
1.2 胸型分类
由于采集到的人体数据差异性大且存在误差数据,需要对数据进行筛选、精简、降噪、对称等前处理操作来确保数据的有效性。在保证人体特征点清晰的前提下,消除噪点影响,从而获得较为光滑的人体数据。剔除误差数据后,保留114名人体数据。
通过提取乳房轮廓特征点来构建胸部的局部坐标系。本文提取乳底点(BBP)、乳房外缘点(OBP)、乳房内缘点(IBP)和乳点(BP)作为乳房特征点[12],将BBP点、OBP点、IBP点连接,建立YZ坐标平面,经过BP点且法线为OBP点和IBP点连线的面作为XZ坐标平面,经过BP点且与YZ平面和XZ平面垂直的面作为XY坐标平面,三个坐标平面的交点为原点O,使用对齐坐标功能构建局部坐标,如图1(a)所示。将BP点到O点的距离作为乳房深a,将OBP点和IBP点的距离作为胸宽b,如图1(b)所示。
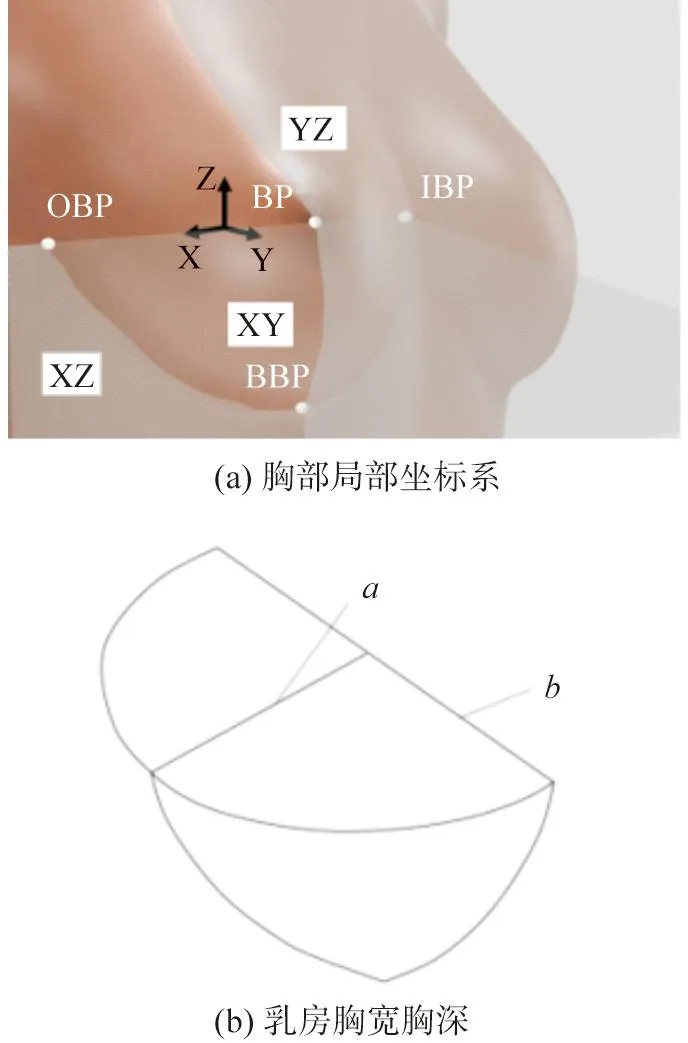
图1 局部坐标系
为建立有限元模型,探究不同胸型下的受压情况,需对受试者进行胸型分类。本文选取能够较好体现胸型形状差异的胸深宽比(Depth Width Ratio,DWR)来对胸型进行分类[9]。此方法将乳房深a与乳房宽b的比值作为分类指标,分类时胸型覆盖率较高[13]。对样本进行分类,能够体现胸部形态差异及胸型特点。根据DWR值的大小范围将114名人体数据分为6类胸型,DWR值越大,乳房形状越突出且起伏越大。胸型及对应的样本数如表1所示。
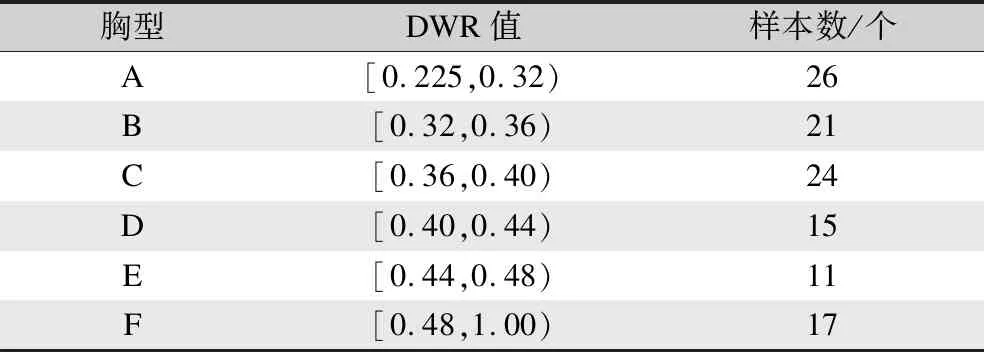
表1 胸型分类及样本数
1.3 几何曲线装配
截取114个人体模型过BP点的水平截面作为胸围截面,在截面曲线上以胸宽为横轴,胸厚为纵轴构建坐标系,利用Matlab编程对截面曲线进行平滑和提取数据坐标点处理,每5°定一个坐标点,共划分为72个点,将每类胸型下的坐标数据进行平均化处理[14]。本文将女体胸围截面曲线作为皮肤层,得到6种胸型的皮肤层曲线。
软组织层包括输乳管窦、乳腺、肌肉等内部结构[6],位于皮肤层内部,其坐标数据根据皮肤层和皮肤层厚度计算可得。女体胸部皮肤层厚度为1.5 mm[14],利用Matlab编程,分别将6类胸型皮肤层坐标值导入,分类获取胸围截面处软组织层坐标值,计算如下式所示。
(1)
式中:x0代表几何模型皮肤层曲线上任意一个点的x坐标,y0代表几何模型皮肤层曲线上任意一个点的y坐标,x代表软组织层曲线上与皮肤层相对应的点的x坐标,y代表软组织层曲线上与皮肤层相对应的点的y坐标;d代表皮肤层厚度,θ代表相应点的角度。
骨骼层曲线参照中国可视化女体断层图片[15],重建几何模型中的骨骼层相对位置,进行顺滑、对称处理,获得骨骼层曲线坐标,如图2所示。
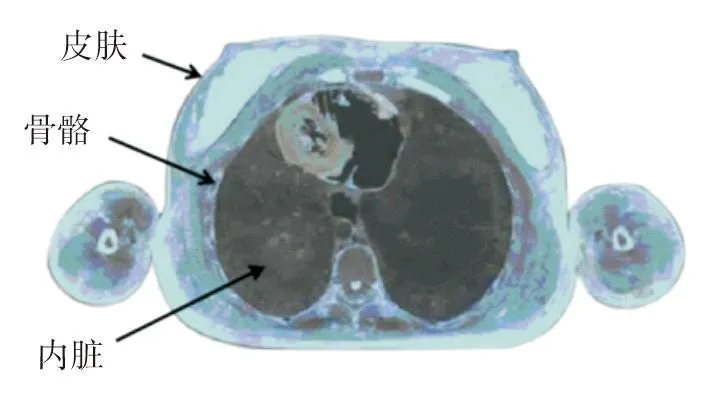
图2 女体胸围截面横向剖面
根据女体真实结构,重建皮肤层、软组织层和骨骼层曲线坐标系,将每层曲线的原点坐标对齐,对截面模型进行几何装配,构建的几何模型作为有限元建模的基础。本文以B胸型为例,每层曲线及几何装配模型如图3所示。

图3 几何模型装配曲线
2 胸围截面有限元建模与仿真
本文基于6种胸型的几何模型,建立有限元模型,施加5种不同大小的压力载荷,模拟不同受压状态下6类胸型所受压力与体表位移的变化规律。在确保模型精度的情况下简化模型,对模型进行假设并提高运算精度确保模型有效性[16]。表2为本文对模型做出的假设。

表2 模型假设条件
把几何模型导入Abaqus中,创建胸围截面各层部件,将胸围截面看作各向同性的弹性体。皮肤层、软组织层、骨骼层材料参数如表3所示[17]。

表3 材料参数
网格类型为CPE3,种子大小为2。设置部件相互作用,使皮肤层、软组织层及骨骼层在边界上连接,但却各自独立,皮肤、软组织、内部骨骼间互相黏接,当受到外部应力时无相对滑移,此时将皮肤层和软组织层接触定义为变形体与变形体的黏结,将软组织层和骨骼层接触定义为变形体与刚体的黏结[18]。由于骨骼在受压后不发生位移,将边界条件设定为骨骼固定,即x方向和y方向位移均为0。
本文基于6类胸型的不同形状特点,研究胸围截面上受体表特征差异影响的不同点处受压位移变化特征。为得出不同胸型受压力影响易产生皮肤形变的位置,对胸围截面施加不同大小的均匀压力。因此,在紧身胸衣舒适范围[19]内施加2、2.5、3、3.5、4.0 kPa的5种法向压力载荷,作用于皮肤表面。探究当受压发生变化时,各胸型受压位移变化规律。边界条件及压力施加情况如图4所示。本文以B类胸型为例,有限元模型如图5所示。

图4 压力施加及边界条件

图5 B类胸型的有限元模型
3 结果与分析
按照DWR值大小得到了6类胸型,不同胸型对应的胸围截面形状、软组织层厚度等差异导致模拟结果和胸围截面压力与位移函数关系有所不同。因此,基于胸型差异本文分别对6类胸型仿真的结果进行分析。
3.1 仿真结果
通过Abaqus有限元分析软件计算,得到在2~4 kPa舒适压力内A、B、C、D、E、F这6类胸型受5种不同大小压力载荷作用下的应力及位移变化情况。图6为受压3 kPa时,6种胸型所受应力情况。由图6可知,乳房位置应力最大,约为2 kPa;其次是后侧位置,约为1.7 kPa。故可知,在外力作用下,曲率较大且位置突出处应力较大。
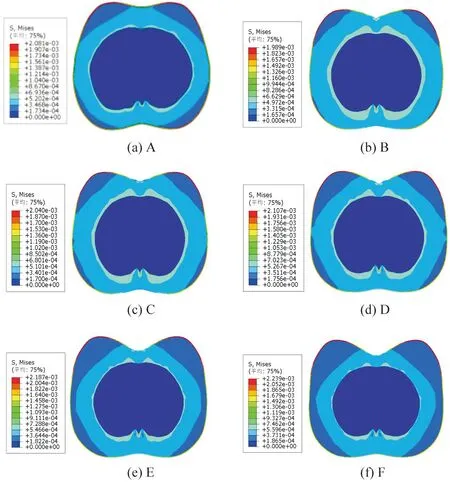
图6 3 kPa压力下不同胸型应力云图
图7为受压3 kPa时,6类胸型的位移云图。由图7可知,A胸型的形变较大处集中在靠近胸高点并偏向前中的位置,形变较为集中。从A胸型向F胸型过渡的过程中,乳房表面形态起伏逐渐变大,胸部软组织层变厚,形变逐渐从胸高点向侧面位置分散增加,但形变最大位置始终在BP点附近,随胸型变化增大呈现外扩趋势。

图7 3 kPa压力下不同胸型位移云图
3.2 胸围截面压力、位移与角度函数关系
体表的受压变形量是表征人体压力舒适性及紧身衣设计的理论依据。本文在前期数据预处理阶段,通过相关性分析得出“压力/位移”作为整体时与角度间的相关性较高,6类胸型的拟合度较高,R2均大于0.95。因此,以角度为自变量,“压力/位移”为因变量,探究不同胸型压力、位移与角度间的函数关系。根据“压力/位移”值,可通过易测得的压力数据计算难以常规测量的体表位移数据,建立压力与体表位移间的关系。对A~F这6类胸型“(压力/位移)—角度”的函数关系曲线分段进行拟合,有助于对以胸围为依据的紧身服装设计进行优化。由于对胸型曲线进行了平均、对称等标准化处理,在[180°,360°]的数据以x=180°为对称轴与[0°,180°]对称,因此,本文仅对[0°,180°]“压力/位移—角度”的函数关系进行拟合,并得出曲线函数及其相应拟合度,如图8所示。拟合函数及拟合度如表4所示,其中,x为角度,y为“压力/位移”值。

表4 A~F胸型的“(压力/位移)—角度”函数关系
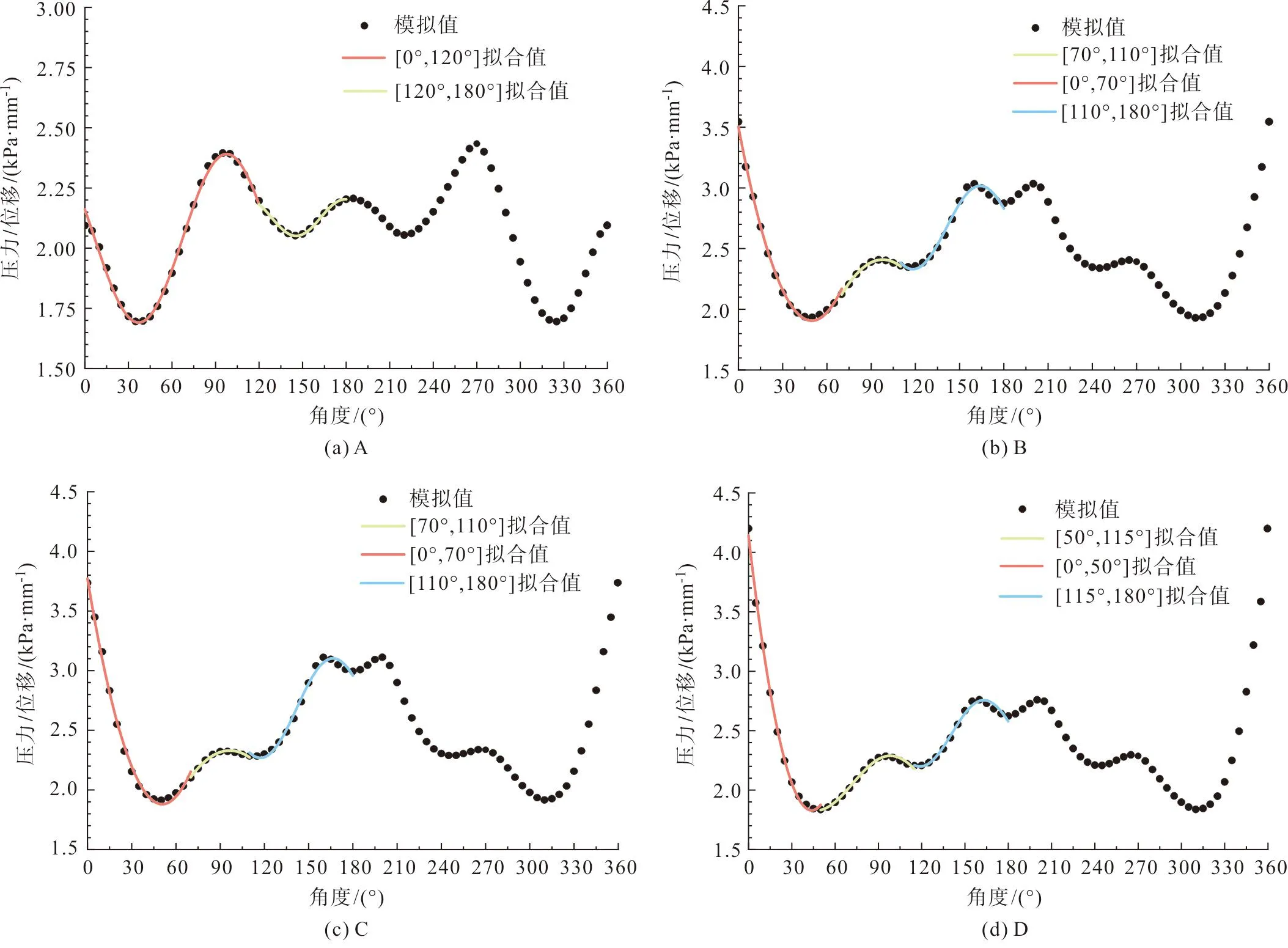

图8 A~F胸型“(压力/位移)—角度”函数关系拟合曲线
由表4可知,在[0°,180°]内,A胸型分两段进行拟合,B~F胸型分三段进行拟合,其拟合曲线的拟合度(R2)均在0.99左右。根据拟合函数,也可以得知不同胸型下特定压力时的位移大小。因压力相对于体表位移更易获得,根据压力计算的位移值是评价压力舒适性及紧身服装塑形美观效果的重要指标,利用此拟合函数,可以高效、准确地得到体表位移值这一关键数据。
3.3 基于不同胸型的压力位移变化规律分析
3.3.1 不同胸型的体表位移变化规律
图9为5种压力作用下人体的位移曲线。由图9可知,在不同压力作用下,B、C、D、E、F胸型的曲线整体变化趋势基本一致,随着压力增大,位移也随之增大,曲线整体呈现上移趋势,胸型之间的位移差也是递增的。在不同压力作用下,A胸型在0°和180°位置的形变始终大于其他胸型。
B、C、D、E、F胸型形变最大点均在50°和310°左右。而受BP点位置影响,A胸型的形变最大点在35°和325°左右。B、C、D、E、F胸型形状相对A胸型较外扩,每类胸型形变最大点和其对应的BP点位置一致,越接近BP点,形变就会越大。
B、C、D、E、F胸型形变最小点在0°左右,即前中位置。A胸型的形变最小点在90°~95°,对应人体侧缝位置。这6类胸型在0°附近位移变化按顺序递减,此位置处A胸型位移变化最大,形变值为E胸型的2倍左右。
对于B、C、D、E、F胸型,仅次于最低点的极小值点出现在160°和200°附近,即180°对应的胸围截面的后中位置附近。这是由于A胸型女体偏瘦,其90°和270°附近的人体侧缝位置软组织层厚度较薄且基本小于A胸型胸围截面的其他位置,导致最小形变量出现在该位置附近;而B~F胸型软组织层最薄处位于0°附近,同时后中180°附近位置也相对较薄的,仅次于0°位置,0°和180°±20°分别与最小位移变化和极小值点的位置相对应。因此,胸型影响下的软组织层厚度和受压位移密切相关,受不同胸型形态起伏及软组织层厚度规律影响,相同压力下,软组织层较薄的位置,其位移变化较小。
3.3.2 不同压力下的体表位移变化规律
图10为6种胸型在不同压力下的位移变化规律。由图10可知,6种胸型体表的位移变化规律基本一致,和每类胸型的体表形态特征变化一致。随着压力增大,体表各处形变呈递增趋势。从前中到胸高点位置,位移随体表形态变化逐渐增大,再过渡到侧缝位置,随软组织厚度减小,形变相应减少。从侧缝至后侧120°左右位置,位移值随软组织变厚相应增加,最后向后中方向总体呈下降趋势,180°~360°和0°~180°对称变化。

图10 A~F胸型位移随压力变化曲线
4 结 论
受不同胸型的截面形态差异影响,受压后胸围截面发生的形变规律随胸型变化呈现不同特点。本文根据乳房轮廓特征参数差异将114名人体数据细分为6类,针对每类胸型特点分别建立有限元数值模型,对其施加5种均匀大小的法向压力,研究胸型差异下胸围截面压力与位移变化规律,并拟合得到了“(压力/位移)—角度”曲线及其函数关系,主要结论如下:
1) 6类胸型受5种不同大小压力载荷作用下,胸围截面BP点应力最大,其次是后侧位置,曲率较大且位置突出处应力较大。
2) 在压力作用下,A胸型的形变主要集中在靠近胸高点并偏向前中的位置,产生的位移变化比较集中。而从A胸型向F胸型过渡的过程中,由于乳房表面起伏形态逐渐变大,胸部及人体侧面软组织层变厚,形变随胸型变化增大且呈现外扩趋势,但形变最大的位置始终在BP点附近。
3) 基于胸型特点构建了6类胸型压力、位移和角度间三角函数关系,拟合度(R2)均在0.99左右,拟合效果较好。由于实际皮肤表面形变不易通过测量直接获得,可以在已知压力数据情况下即可求得体表形变数据,替代了受压位移繁琐的测量,从而简化测量步骤,可为紧身服装压力舒适性研究提供参考。

《丝绸》官网下载

中国知网下载
