NOTES ON THE LOG-BRUNN-MINKOWSKI INEQUALITY∗
2023-12-14杨云龙江楠
(杨云龙) (江楠)
School of Science, Dalian Maritime University, Dalian 116026, China
E-mail: ylyang@dlmu.edu.cn; 995125315@qq.com
Deyan ZHANG (张德燕)†
School of Mathematical Sciences, Huaibei Normal University, Huaibei 235000, China
E-mail: zhangdy8005@126.com
Abstract Böröczky-Lutwak-Yang-Zhang proved the log-Brunn-Minkowski inequality for two origin-symmetric convex bodies in the plane in a way that is stronger than for the classical Brunn-Minkowski inequality.In this paper,we investigate the relative positive center set of planar convex bodies.As an application of the relative positive center,we prove the log-Minkowski inequality and the log-Brunn-Minkowski inequality.
Key words cone-volume measure;dilation position;log-Brunn-Minkowski’s inequality;log-Minkowski’s inequality;relative positive center
1 Introduction
We denote the usualn-dimensional Euclidean space with Rnas the canonical inner product.A compact convex setK ⊆Rnis a convex body if it contains the origin and has a nonempty interior.Whenn=2,it is called a planar convex body.For two convex bodies,KandL,the Minkowski sum ofKandLand the Minkowski scalar product ofKfor a positive real numbertare defined,respectively,byK+L={x+y|x ∈K,y ∈L} andtK={tx|x ∈K}.LetKandLbe two convex bodies in Rnandλ ∈(0,1).The classical Brunn-Minkowski inequality states that
whereV(·) denotes then-dimensional volume (i.e.,the Lebesgue measure) functional.The equality in (1.1) holds if and only ifKandLare homothetic.The inequality (1.1) has become a significant tool in convex geometry,and it has extensive applications in various areas of mathematics.More comprehensive introductions to this topic can be found in Gardner’s review[11]and Schneider’s monograph [32].
In the early 1960s,Firey [8](see also Gardner-Hug-Weil [12,p2311]and Schneider [32,Section 9.1]) extended the Minkowski addition of convex bodies to theLpMinkowski addition for eachp ≥1 and established theLpBrunn-Minkowski inequality;that is,
with equality if and only ifKandLare dilates,where
is theLpMinkowski addition ofKandL,andhKandhLare the support functions ofKandL,respectively.Lutwak [23,24]set up a broad framework for theLpBrunn-Minkowski theory and promoted it for rapid development.TheLpBrunn-Minkowski theory,as a generalization of the classical Brunn-Minkowski theory,has attracted increasing interest in recent years,partly due to its wide range of connections with other subjects,such as affine geometry,Banach space theory,harmonic analysis,and partial differential equations.
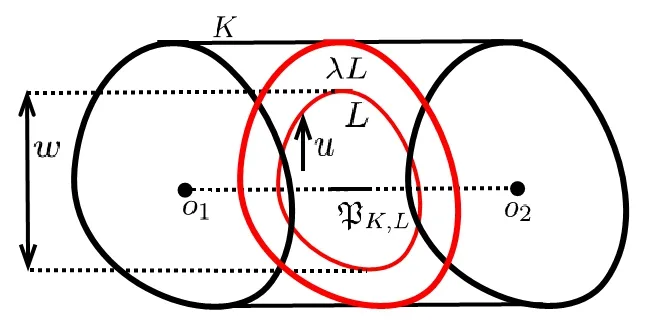
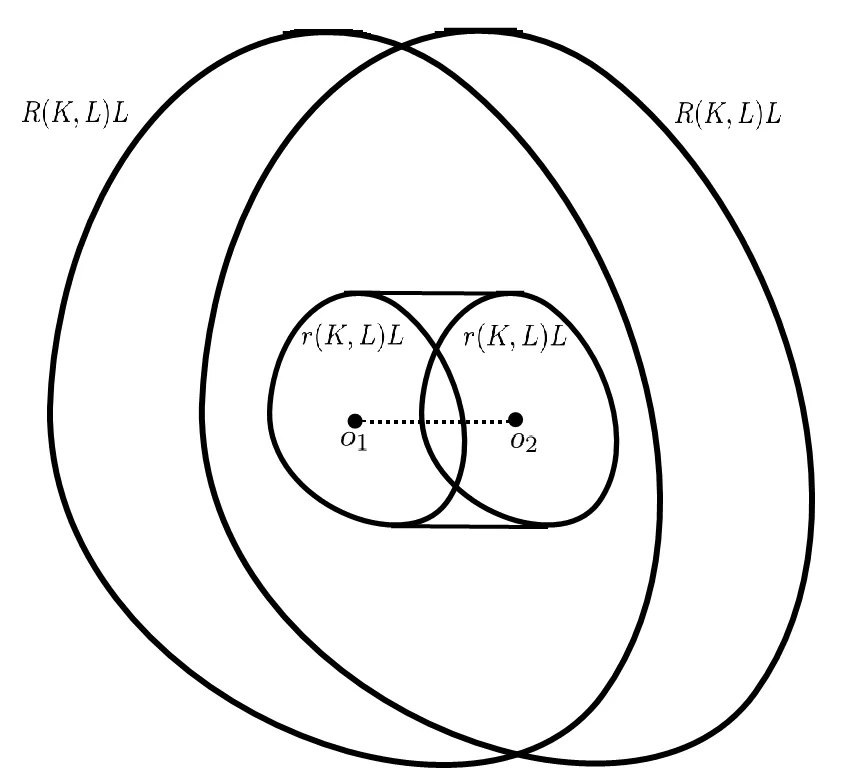
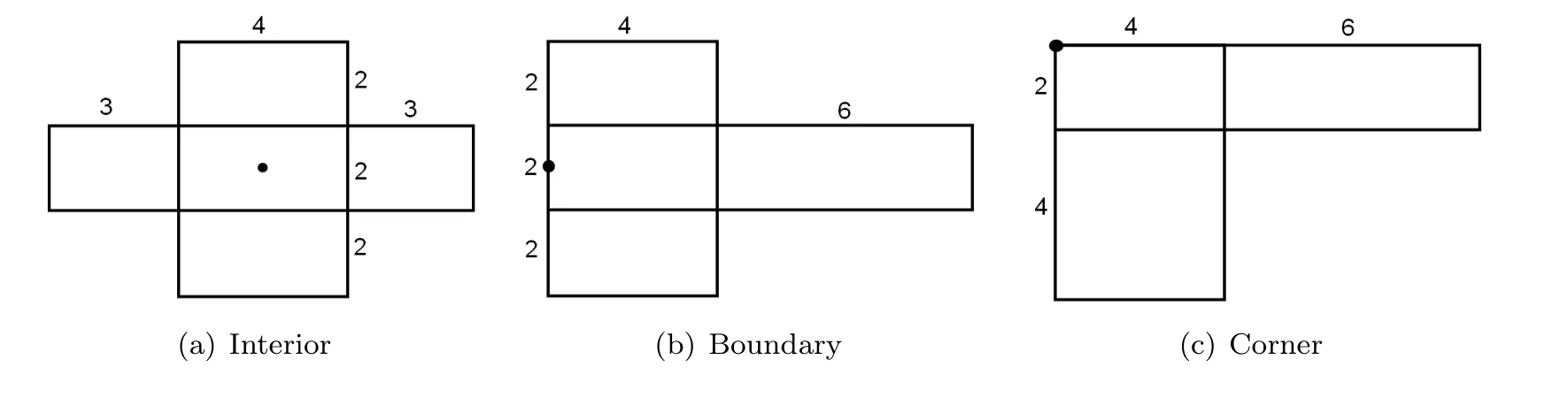
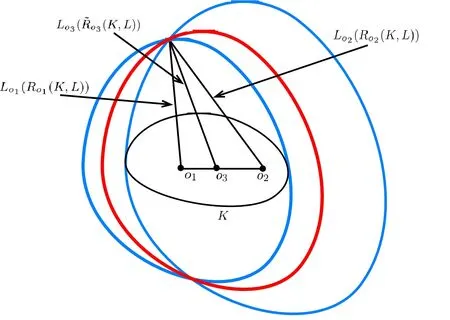
Böröczky-Lutwak-Yang-Zhang [2]extended (1.3) into allp>0.For the case 0 which is the limiting case of theLpMinkowski addition asp →0. In [2],the authors conjectured that the log-Brunn-Minkowski inequality and the log-Minkowski inequality hold for two o-symmetric convex bodiesKandL,whereis the cone-volume probability measure ofKandλ ∈[0,1]. Xi-Leng [37]composed the definition of a “dilation position”,and obtained the log-Brunn-Minkowski inequality and the answer to Dar’s conjecture for when two planar convex bodies are in a dilation position.Ma [25]gave an alternative proof of (1.5) for the planar case.Saroglou[30]established (1.4),together with its equality cases for pairs of convex bodies that are both unconditional with respect to some orthonormal basis,and dealt with generalizations of (1.4)in [31].Stancu [35]proved some variants of the logarithmic Minkowski inequality for general convex bodies and developed some special cases for the equality in(1.5)without the symmetric assumption.Other aspects of the log-Brunn-Minkowski and log-Minkowski inequalities can be found in Colesanti-Livshyts-Marsiglietti [5],Colesanti-Livshyts [6],Eskenazis-Moschidis [7],Henk-Pollehn [16],Kolesnikov-Milman [22],Putterman [27],Rotem [28],Roysdon-Xing [29],Yang-Zhang [41],Yang-Yang-Zhu [39],etc.. This paper aims to show proofs of the log-Brunn-Minkowski and log-Minkowski inequalities for when two planar convex bodies are at a dilation position.Distinct from Xi-Leng’s technique,our proof is based on the relative positive center of convex bodies (see Definition 2.2),which is a generalization of the positive center given by Gage [9]. The aspect of“dilation position”is the key to the work of Xi-Leng[37].The most important of our proof is establishing a connection between the “dilation position” and the “relative positive center”.Concretely,we obtain the following proposition by comparing these definitions: Proposition 1.1LetKandLbe two planar convex bodies.IfKandLare at a dilation position and the origino ∈int(K ∩L),thenomust be a relative positive center ofKwith respect toL. To describe the positive center set of planar convex bodies,we have the following two theorems: Theorem 1.2LetKandLbe two planar convex bodies.IfKandLare at a dilation position and the origino ∈int(K ∩L),then the relative positive center set ofKwith respect toL,βK,Lis a closed convex set,and for any boundary pointxof βK,L,at least one ofBK,L(rx(K,L))=0 andBK,L(Rx(K,L))=0 holds. Theorem 1.3LetKandLbe two planar convex bodies.IfKandLare at a dilation position and the origino ∈int(K ∩L),then the relative positive center set ofKwith respect toL,βK,Lis a closed convex set and (i)βK,Lhas only one point if and only ifKandLare dilates or parallelograms with parallel sides; (ii) βK,Lis a line segment if and only if eitherKis a Minkowski addition of a dilation ofLand a line segment orLis a Minkowski addition of a dilation ofKand a line segment; (iii) βK,Lhas a positive area if and only ifKandLare neither (i) nor (ii). As applications regarding the positive center set of planar convex bodies,we have the following log-Minkowski and log-Brunn-Minkowski inequalities for when two planar convex bodies are at a dilation position (obtained by Xi-Leng [37]): Theorem 1.4LetKandLbe two planar convex bodies.IfKandLare at a dilation position,then with equality if and only ifKandLare dilates or parallelograms with parallel sides. Theorem 1.5LetKandLbe two planar convex bodies.IfKandLare at a dilation position,then,forλ ∈[0,1], Whenλ ∈(0,1),the equality in(1.7)holds if and only ifKandLare dilates or parallelograms with parallel sides. The rest of this paper is organized as follows: Section 2 presents some concepts and lemmata about convex bodies.Section 3 discusses the relative positive center set of two planar convex bodies when they are at a dilation position,and shows the proofs of Theorems 1.2 and 1.3.Section 4 proves Theorems 1.4 and 1.5 via the positive center set of planar convex bodies. This section reviews some basic notations and definitions in convex geometry.Good general references for the theory of convex bodies are provided by the books of Gardner [11],Gruber[13],Schneider [32]and Thompson [36]. LetSn-1be the(n-1)-dimensional unit sphere.Forx,y ∈Rn,x·yrepresents the standard inner product ofxandy.The forms intAand∂Adenote the interior and boundary ofA ⊆Rn.[M,N]denotes the line segment connecting pointsMandN. IfKis a convex body in Rn,its support functionhK:Rn →R ishK(x)=max{x·y|y ∈K}. For a convex bodyKin Rn,its surface area measureSKis a Borel measure onSn-1defined for a Borel setω ⊆Sn-1by whereνK:∂′K →Sn-1is the Gauss map ofK,defined on∂′K,the set of points of∂Kthat have a unique outer unit normal,andHn-1is the (n-1)-dimensional Hausdorffmeasure. LetKbe a convex body containing the origin in its interior.The cone-volume measureVKofKis a Borel measure on the unit sphereSn-1defined for a Borel setω ⊆Sn-1as the cone-volume probability measureofKis defined by The cone-volume measure plays a significant role in the log-Minkowski problem.Many works have recently focused on this subject;see,e.g.,[1,3,4,10,14,15,17,19,33,34,38,42]. Suppose thatKandLare two convex bodies in Rn.The relative Steiner formula states that whereVi(K,L) is thei-th mixed volume ofKandL.In particular,one has thatV0(K,L)=V(K),Vn(K,L)=V(L),Vi(K,L)=Vn-i(L,K),and Then,V1(K,L)=V1(L,K) forn=2,and for the rest of this paper,we denote thatV(K,L)rather thanV1(K,L).Forn=2,Equation (2.2) becomes be the inradius and outradius,respectively,ofKwith respect toL.Thus, Forx ∈K,setrx(K,L)=max{t ≥0|x+tL ⊆K} andRx(K,L)=min{t ≥0|x+tL ⊇K}.Ifx ∈K ∩L,then Definition 2.1([37]) LetK,Lbe two planar convex bodies.KandLare at a dilation position if the origino ∈K ∩Landr(K,L)L ⊆K ⊆R(K,L)L. The properties of convex bodies are at a dilation position,as found in Lemma 3.2 (see also Xi-Leng[37]).Some papers recently considered the dilation position;these include Jin[20]and Yang [40].By the relative Bonnesen function ofKwith respect toL, we give the following definition of the relative positive center: Definition 2.2LetK,Lbe two planar convex bodies.A pointx ∈intKis a relative positive center ofKwith respect toLif it satisfies that Ifx ∈int(K ∩L) andxis a relative positive center ofKwith respect toL,thenxis the relative positive center ofLwith respect toK.The set of all relative positive centers ofKwith respect toLare denoted as βK,L.WhenLis the unit disc,the relative positive center turns into the positive center.The positive center set of plane curves was studied by [18,21,26]. For the remainder of this paper,for a planar convex bodyE,Ex(r) represents the planar convex bodyx+rE. To show the relationship between the relative positive center and the dilation position of planar convex bodies,we give two lemmata which appeared in Böröczky-Lutwak-Yang-Zhang[2]and Xi-Leng [37]. Lemma 3.1([2]) IfKandLare two planar convex bodies,then,forr(K,L)≤t ≤R(K,L), This inequality is strict wheneverr(K,L) Lemma 3.2([37]) LetKandLbe two convex bodies in Rn.Then, (i) there are a translate ofL,say,and a translate ofK,say,so thatandare at a dilation position; (ii) ifKandLare at a dilation position,then the origino ∈int(K ∩L)∪(∂K ∩∂L). The next three examples show that the relative positive center set ofKwith respect toL,βK,L,has only one point,and that it is a line segment. Example 3.3LetKandLbe two planar convex bodies.If they are dilates,then a simple computation shows that the relative positive center set ofKwith respect toL,βK,L,has only one point which is the center of dilation. Example 3.4LetKandLbe two parallelograms with parallel sidesa,candb,d(see Figure 1).The areas ofKandLareV(K)=acsinθandV(L)=bdsinθ,respectively,and the mixed area ofKwith respect toLisV(K,L)=(ab+cd)sinθ.Hence, Figure 1 The case of two parallelograms A simple computation shows that there is only one point (black dot in Figure 1) that satisfiesBK,L(t)≥0;that is,βK,Lhas only one point. Example 3.5LetKandLbe two planar convex bodies.IfK=λL+[o1,o2],whereλ>0 and [o1,o2]is a line segment of lengths,the area ofKisV(K)=λ2V(L)+λws,wherewis the width ofLin theudirection,which is normal to [o1,o2](see Figure 2).The mixed area ofKwith respect toLisHence, Figure 2 The case where K=λL+[o1,o2] A simple computation shows that βK,Lis a line segment. For two planar convex bodiesKandL,the following proposition shows that the relative positive center set is not empty whenKandLare at a dilation position: Proof of Proposition 1.1AsKandLare at a dilation position and the origino ∈int(K ∩L),r(K,L)L ⊆K ⊆R(K,L)L,comparing Definitions 2.1 and 2.2,one has thatro(K,L)=r(K,L) andRo(K,L)=R(K,L).It follows from Lemma 3.1 that Similarly,BK,L(Ro(K,L))≥0.Hence,the origin is the positive center ofKwith respect toL. Lemma 3.6LetKandLbe two planar convex bodies.IfKandLare at a dilation position and the origino ∈int(K ∩L),then the choice of originowith respect toKandLis unique. ProofSuppose that there exist two pointso1ando2such thato1∈int(K ∩L),o2∈int(K ∩L),and Then,Kbelongs to the intersection ofo1+R(K,L)Lando2+R(K,L)L,and contains the convex hull ofo1+r(K,L)Lando2+r(K,L)L.Figure 3 shows that there existso3∈(o1,o2)such that Figure 3 Illustration that the choice of origin is non-unique which contradicts the definitions ofr(K,L)andR(K,L);that is,the choice of the originowith respect toKandLis unique. The choice of the origin for planar convex bodies that are at a dilation position may vary as translations of the planar convex bodies. Remark 3.7The black dots in Figure 4 are the choices of the origins for two rectangles with sides of 4,6 and 2,10. Figure 4 Different choices of the origin as translations Proof of Theorem 1.2By Proposition 1.1,the originomust be the relative positive center ofKwith respect toLwhenKandLare at a dilation position ando ∈int(K ∩L);that is,βK,Lis not empty.From the definition of the relative positive center,βK,Lis closed,and for any boundary pointxof βK,L,at least one ofBK,L(rx(K,L))=0 andBK,L(Rx(K,L))=0 holds.Thus,it suffices to show that βK,Lis convex.If βK,Lhas only one point,its convexity is clear.If βK,Lhas more than one point,it is sufficient to show that for two relative positive centers ofKwith respect toL,o1ando2,the pointo3∈[o1,o2]is also a relative positive center ofKwith respect toL.In other words,one has to check that wheret1andt2(t1≤t2) are two roots ofBK,L(t)=0. AsKis convex,it containsLo1(ro1(K,L)),Lo2(ro2(K,L)),andLo3((K,L)).Figure 5 shows that Figure 5 Inscribed case Figure 6 shows thatLo1(Ro1(K,L)),Lo2(Ro2(K,L)) andLo3((K,L)) containK,which implies Figure 6 Circumscribed case Combining (3.2) and (3.3) and the fact thato1,o2∈βK,Lando1≠o2,we have that that is,o3is a point of βK,L. Theorem 1.2 shows that the relative positive center set of planar convex bodies is a closed convex set. Proposition 3.8LetKandLbe two planar convex bodies.IfKandLare at a dilation position and the origino ∈int(K ∩L),then βK,Lhas only one point if and only ifKandLare dilates or parallelograms with parallel sides. ProofExamples 3.3 and 3.4 show that βK,Lhas only one point whenKandLare dilates or parallelograms with parallel sides.Thus,it suffices to deal with the “only if” part. AsKandLare at a dilation position and the origino ∈int(K ∩L),Proposition 1.1 and Lemma 3.6 indicate thatois the only point of βK,L.By the definition of the relative positive center and dilation position of planar convex bodies,one has thatro(K,L)=r(K,L) andRo(K,L)=R(K,L).Theorem 1.2 states that at least one of the following equalities holds: Together with Lemma 3.1,this implies thatKis the Minkowski addition of a dilation ofLand a line segment or thatLis the Minkowski addition of a dilation ofKand a line segment.Thus,KandLare dilate and parallelograms with parallel sides,orKis a Minkowski addition of a dilation ofLand a line segment,orLis a Minkowski addition of a dilation ofKand a line segment.IfK(L) is a Minkowski addition of a dilation ofL(K) and a line segment,Example 3.5 shows that βK,Lis a line segment,which contradicts to the assumption that βK,Lhas only one point. Proposition 3.9LetKandLbe two planar convex bodies.IfKandLare at a dilation position and the origino ∈int(K ∩L),then βK,Lis a line segment if and only ifKis a Minkowski addition of a dilation ofLand a line segment orLis a Minkowski addition of a dilation ofKand a line segment. ProofExample 3.5 suggests that βK,Lis a line segment whenKis a Minkowski addition of a dilation ofLand a line segment,orLis a Minkowski addition of a dilation ofKand a line segment.Next,it suffices to deal with the “only if” part. If βK,Lis a line segment,Proposition 1.1 and Lemma 3.6 show that the originomust be the boundary point of βK,L.From the definition of the relative positive center and the dilation position of planar convex bodies,it follows thatro(K,L)=r(K,L) andRo(K,L)=R(K,L).Thus,similarly to the proof of Proposition 3.8,one has that which,together with Lemma 3.1,shows thatKis the Minkowski addition of a dilation ofLand a line segment,orLis the Minkowski addition of a dilation ofKand a line segment.Hence,KandLare dilates or parallelograms with parallel sides orK(L) is a Minkowski addition of a dilation ofL(K) and a line segment.IfKandLare dilates or parallelograms with parallel sides,Examples 3.3 and 3.4 suggest that βK,Lis a point,which contradicts the fact that βK,Lis a line segment. Proof of Theorem 1.3By Propositions 3.8 and 3.9,one gets the desired result. Remark 3.10Theorems 1.2 and 1.3 can be regarded as generalizations of Theorems 2.1,2.6 and 2.7 from Huang-Pan-Yang [18],for when a planar convex bodyLis chosen as a unit disc. Inspired by the work of Böröczky-Lutwak-Yang-Zhang [2],Xi-Leng [37]and Ma [25],we first give the following technical lemma: Lemma 4.1LetKandLbe two planar convex bodies.IfKandLare at a dilation position,then fort ≥0, with equality if and only ifKandLare dilates or parallelograms with parallel sides. ProofBy Lemma 3.2,the origin iso ∈int(K ∩L)∪(∂K ∩∂L).To prove the inequality(4.1),it is sufficient to show the following two cases: Case 1o ∈int(K ∩L). which,together with (2.3),gives that which implies the desired inequality (4.1). IfKandLare dilates or parallelograms with parallel sides,the equality holds in (4.1).To prove thatKandLare dilates or parallelograms with parallel sides when the equality holds in(4.1),it is enough to show that the inequality (4.1) is strict whenKandLare neither dilates nor parallelograms with parallel sides. Case 2o ∈∂K ∩∂L. Aso ∈∂K ∩∂L,for allu ∈S1Σ2(Σ2as Case 1),then in a fashion similar to the proof of Case 1,one can get inequality (4.1).IfKandLare dilates or parallelograms with parallel sides,the equality holds in (4.1). If the equality holds in (4.1),then for allu ∈suppSK Σ2.By Lemma 3.1,one has that for allu ∈suppSK Σ2.AsKis a convex body,Σ2must be contained in an open subset of a half-sphere,and suppSKcannot be concentrated on a half-sphere.Thus,suppSK Σ2≠∅.Without loss of generality,we assume that there is anu′∈suppSK Σ2such thathK(u′)=r(K,L)hL(u′).From Lemma 3.2 and its proof (see [2,Lemma 4.1]or [37,p.65]),it follows thatK=r(K,L)L+σ1,whereσ1is a line segment.Thus, for allu ∈S1,andobelongs to the relative boundary ofσ1. Note thatKandLare dilates if and only ifσ1={o}.IfKandLare not dilates,thenσ1is nondegenerate.From expression (4.3) and withobelonging to the relative boundary ofσ1,it follows that the set Σ′={u ∈S1|hK(u)=r(K,L)hL(u)} is contained in a half-sphere.AsKhas interior points,suppSKcannot be concentrated on a half-sphere.This,together with the fact that Σ′is contained in a half-sphere,shows that suppSKΣ′must contain at least one unit vectoru′′.By (4.2) and the fact Σ2⊆Σ′,one has thatSimilarly, whereobelongs to the relative boundary ofσ1.Again,expression (4.3) yields that Note thatKandLare not dilates if and only ifThus, which implies thatKis a parallelogram with sides parallel toσ1andσ2.Similarly,one has that which indicates thatLis also a parallelogram with sides parallel toσ1andσ2. Motivated by the work of Ma[25],we can get Theorem 1.4,and its proof is nearly the same as in [25].To ensure the integrity of this article,we provide the detailed proof. Proof of Theorem 1.4Set DifferentiatingF(t) with respect totgives that It follows from (3.1) thatF(t) is decreasing on [0,+∞).The desired results can be achieved if we show thatF(0)≥F(t)≥0 fort ∈[0,+∞).As the mean value theorem for integrals indicates that there is aµ∈S1such that IfKandLare dilates or parallelograms with parallel sides,then the equality holds in(1.6).To prove thatKandLare dilates or parallelograms with parallel sides when the equality holds in (1.6),it is sufficient to show that the inequality (1.6) is strict whenKandLare neither dilates nor parallelograms with parallel sides. Suppose thatKandLare neither dilates nor parallelograms with parallel sides.Lemma(4.1) shows that which implies thatF(t) is strictly decreasing on [0,+∞).Thus,F(0)>F(t)≥0.That is,the inequality (1.6) is strict. Similarly to the proof of [2,Lemma 3.2],one has the following proposition: Proposition 4.2LetKandLbe two planar convex bodies.IfKandLare at a dilation position,then the log-Brunn-Minkowski inequality and the log-Minkowski inequality are equivalent. Proof of Theorem 1.5By Theorem 1.4 and Proposition 4.2,one has the log-Brunn-Minkowski inequality. Conflict of InterestThe authors declare no conflict of interest.2 Preliminaries
3 Relative Positive Center Set of Planar Convex Bodies


4 Planar log-Brunn-Minkowski and log-Minkowski Inequalities
猜你喜欢
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- BIFURCATION CONTROL FOR A FRACTIONAL-ORDER DELAYED SEIR RUMOR SPREADING MODEL WITH INCOMMENSURATE ORDERS∗
- THEORETICAL RESULTS ON THE EXISTENCE,REGULARITY AND ASYMPTOTIC STABILITY OF ENHANCED PULLBACK ATTRACTORS:APPLICATIONS TO 3D PRIMITIVE EQUATIONS∗
- ENTIRE SOLUTIONS OF LOTKA-VOLTERRA COMPETITION SYSTEMS WITH NONLOCAL DISPERSAL∗
- GENERAL CONTENTS
- THE EXISTENCE OF GROUND STATE NORMALIZED SOLUTIONS FOR CHERN-SIMONS-SCHRÖDINGER SYSTEMS∗
- AN INFORMATIC APPROACH TO A LONG MEMORY STATIONARY PROCESS∗
