基于FWD的水泥路面板角脱空弯沉分析

戴 震,刘 真,王 翔,王双平

(1.华设设计集团股份有限公司,南京 210001;2.东南大学交通学院,南京 211189)

水泥混凝土路面的脱空状况是评价刚性路面质量的关键因素。水泥混凝土路面通常因为冲刷、沉降等原因,导致路面板底层部分材料局部流失,形成空隙。这些空隙随着时间和重复荷载的作用逐渐扩大,最终演变成板底脱空问题,对路面板的受力状态产生严重影响。这种现象会引发断板、错台等路面病害,危害刚性路面的结构性能[1]。

目前,水泥混凝土路面脱空情况的检测通常采用FWD弯沉试验。通过比较板边中点与板中的弯沉比以及板角与板中的弯沉比来定性判断板底是否存在脱空问题。然而,目前仍然缺乏定量分析方法或标准来评估脱空的范围和严重程度。此外,针对不同接缝传荷能力下的脱空影响分析也存在一定局限性[2]。因此,该研究结合水泥混凝土路面的结构特点和弯沉测试的实际情况,采用正交试验和有限元方法来分析板角弯沉、板边中点弯沉以及它们之间的比值随着路面结构参数、接缝传荷能力和板角脱空尺寸的变化规律,为后续评估板角脱空情况提供了基础。

1 有限元模型的建立

1.1 路面结构参数

根据水泥混凝土路面设计规范[3],确定水泥混凝土面层板尺寸为5.0 m×5.0 m。路面结构组合为水泥混凝土面层+水稳碎石基层+Winker地基结构[4]。为研究各结构层参数对脱空路面弯沉值的影响,具体参数选取范围如表1所示。

表1 路面结构层参数

1.2 接缝模拟

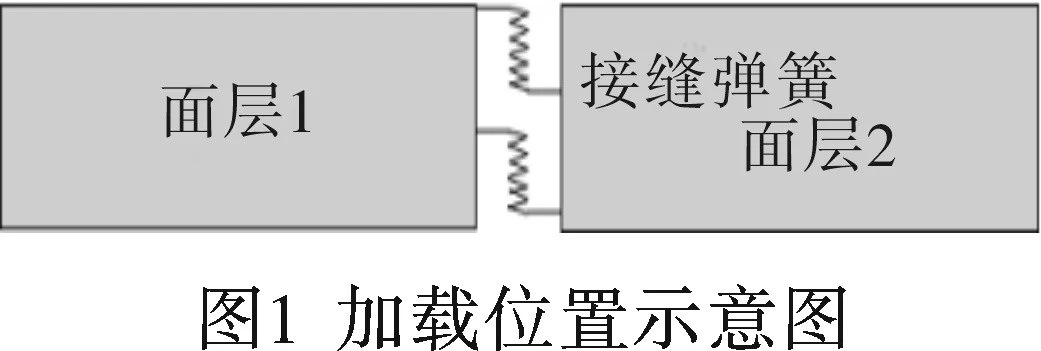
我国水泥混凝土路面接缝具有一定程度的荷载传递能力,主要依靠传力杆设置连接相邻面板来传递竖向剪力。为了建模的便捷,该文选用弹簧单元法进行接缝模拟,在ABAQUS中实体模型离散化生成单元后,采取弹簧单元法连接面层板间对应的网格结点,如图1所示。通过设定法向方向上的弹簧刚度系数来改变接缝刚度的大小,模拟不同状态下的路面接缝状况[5]。根据板角、板边和板中结点的贡献面积程度,计算不同接缝刚度下三种位置结点的接缝弹簧刚度系数,计算式如式(1)所示。

(1)

式中,q为单位长度接缝刚度,MN/m2;λ为接缝长度,m;NR为板侧面结点的行数;NC为板侧面结点的列数;k为板角结点弹簧刚度系数,板边结点弹簧刚度值为2k,板中结点弹簧刚度值为4k,MN/m。

1.3 脱空模拟

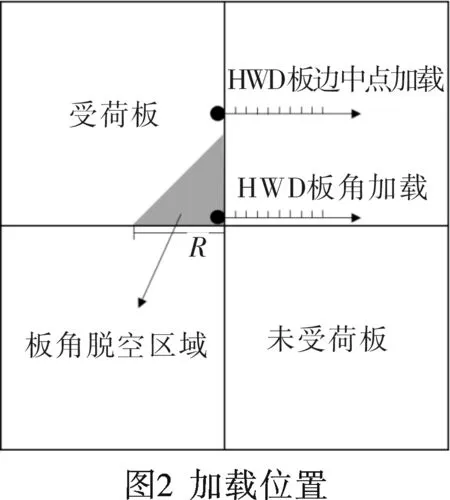
路面脱空是在载荷和环境共同作用下产生的路面内部病害,通常发生在面层板角位置下,表现为基层模量的衰减或者基层材料的缺失。建模过程中将脱空模型的形状在板角处简化为等腰直角三角形[6],脱空尺寸用直角边的边长R来表示。为了研究脱空尺寸对弯沉值的影响,将R的范围设置在0～1.6 m之间。对于脱空区域的设置,选择直接移除脱空区域内的基层材料来模拟脱空导致的基层支承作用的缺失。为简化计算,将原有的动态冲击荷载用静态均布荷载代替,荷载大小统一采用200 kN,作用区域为半径0.15 m的圆形范围,压强为2.83 MPa,作用位置位于板边中点处和板角处,如图2所示。

2 正交试验

2.1 因子水平设计

该研究采用了正交试验,建立了L32(47)正交表来进行试验设计,综合分析了面层模量、面层厚度、基层模量、基层厚度、地基反应模量、接缝刚度以及脱空尺寸对板边中部和板角弯沉值的影响,各个影响因子的水平如表2所示。

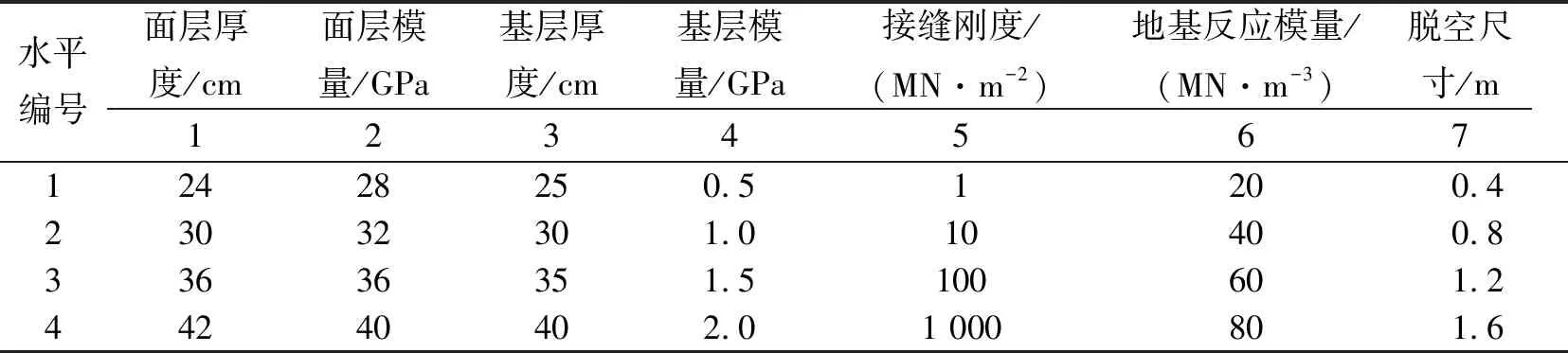
表2 各影响因子水平表

2.2 极差分析

极差是一组数据中最大值与最小值之差,通常用来衡量数据集中的变异性或波动范围。在实验设计和数据分析中,极差可以用来估计各个因素对测试结果的影响程度大小。正交试验的直观分析结果如表3所示,其中Li表示不同影响因素在不同水平时的平均值。当板角发生脱空时,板角处的弯沉值远大于板边中点弯沉值。板边中点弯沉值受面层厚度的影响最大,其次是地基反应模量和接缝刚度。板角处的脱空尺寸对其几乎没有影响。板角弯沉值受面层厚度和接缝刚度影响最大,其次是板角脱空尺寸和地基反应模量。

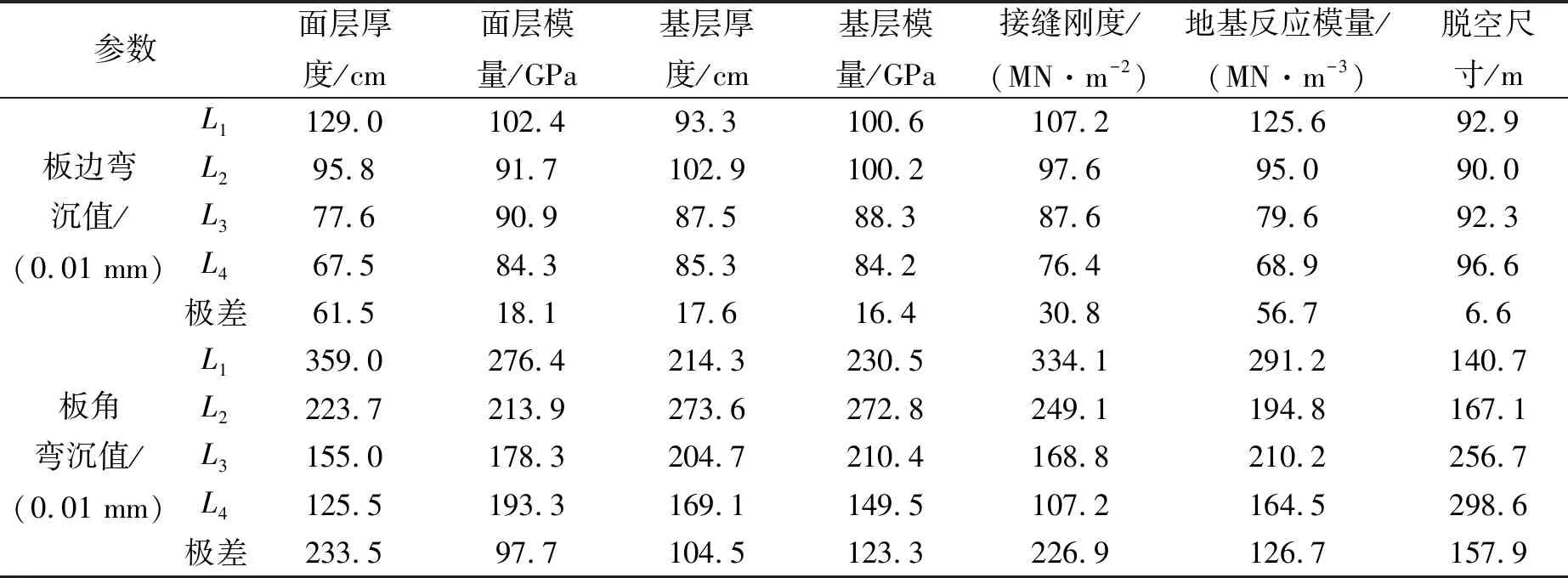
表3 正交试验极差分析结果

3 各弯沉值方差分析

3.1 板角弯沉与板边中点弯沉

多因素方差分析是一种利用方差比较的方法,通过假设检验的过程来判断各个因素是否对因变量产生显著性影响。它的主要目的是排除因素水平的差异和试验误差对观测值的影响,以便确定各个因素的影响程度是否显著。在方差分析中,使用F统计量来比较各个因素的均方,F值越大表示该影响因素与因变量之间的相关性越强。通常,显著性水平(通常设置为0.05)用来判断这种相关性是否显著。当显著性水平P>0.05时,表示该影响因素与因变量之间的关系不显著,而P值越接近于0,则表示相关性越强。

正交试验方差分析结果如表4、表5所示。板边中点弯沉值各因素方差F由大到小分别是地基反应模量>接缝刚度>面层厚度>基层厚度>面层模量>基层模量>脱空尺寸。从这些方差分析结果可以看出,地基反应模量对板边中点弯沉值的影响最大,其次是接缝刚度、面层厚度、基层厚度、面层模量、基层模量,而脱空尺寸对板边中点弯沉几乎没有影响。这些结果表明,地基反应模量是主要影响板边中点弯沉值的因素。而对于板角弯沉值,各因素方差F由大到小分别是接缝刚度>脱空尺寸>地基反应模量>面层厚度>面层模量>基层厚度>基层模量。从显著性分析结果可以看出,接缝刚度和脱空尺寸对板角弯沉值的影响最显著,其他因素的影响相对较小。因此,在评估板角脱空状况时,需要特别关注接缝刚度和脱空尺寸的变化,因为它们对板角弯沉值的影响远大于其他因素。

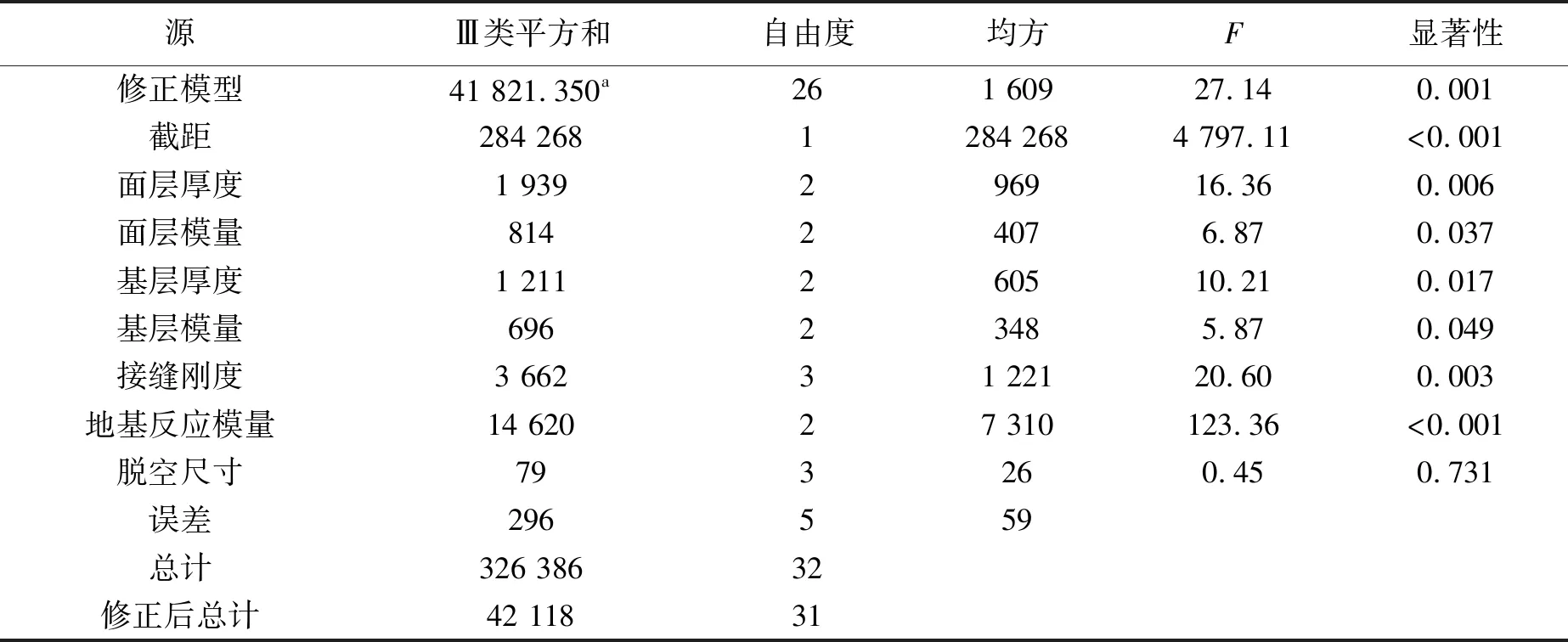
表4 板边中点弯沉方差分析结果

表5 板角弯沉方差分析结果

3.2 板角与板边中点弯沉比

板角弯沉值受接缝刚度和板角脱空尺寸影响较大,受路面结构层参数影响较小。板边中点弯沉值受路面结构层参数与接缝刚度影响较大,受板角脱空尺寸影响较小。对板角弯沉值与板边中点弯沉值之比ω进行各影响因素方差分析可以发现,路面结构层参数(面层厚度、面层模量、基层厚度、基层模量、地基反应模量)对弯沉比ω的显著性均大于0.05,表现为不显著;脱空尺寸和接缝刚度对弯沉比ω的显著性远小于0.05,表现为极为显著,如表6所示。因此,构建板角与板边中点弯沉比ω的指标可以削弱路面结构层参数的影响。

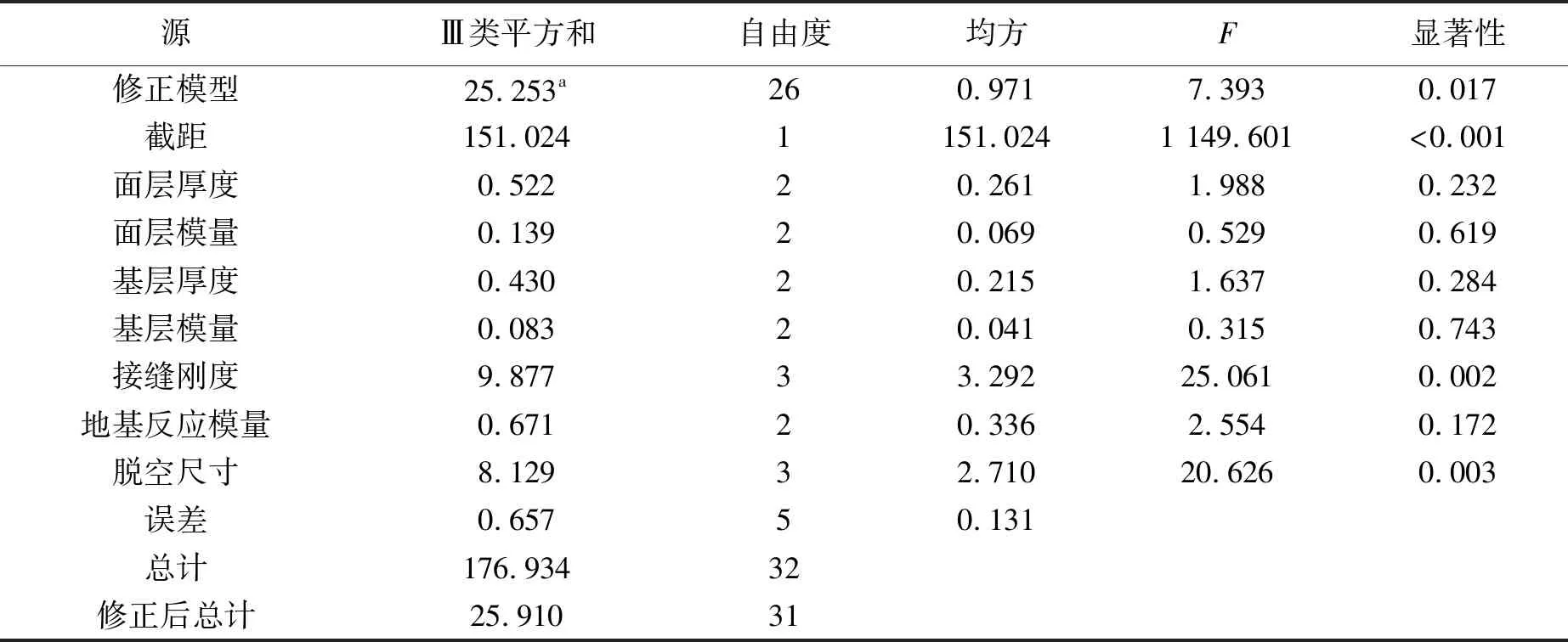
表6 弯沉比ω方差分析结果

4 结 语

该研究建立了基于接缝弹簧单元的水泥混凝土路面板角脱空有限元模型,并采用了正交试验来综合分析面层模量、面层厚度、基层模量、基层厚度、地基反应模量、接缝刚度以及脱空尺寸对板边中部和板角弯沉值的影响。正交试验的极差结果表明,板角脱空尺寸对板边中点弯沉无显著影响,板边中点弯沉受地基反应模量影响最大,其次是接缝刚度和面层厚度。板角弯沉受接缝刚度和脱空尺寸影响比较显著。方差分析结果表明,板角与板边中点弯沉比ω的指标可以削弱路面结构层参数的影响,对比板角弯沉,板角脱空尺寸和接缝刚度对弯沉比ω的P值远小于0.05,显著性更大。这对深入了解水泥混凝土路面板角脱空问题的影响因素和机制具有重要意义,有助于改进和维护道路路面质量。