基于深度强化学习的旅行商问题研究

邹 铁

（雅安开放大学，四川 雅安 625000）

0 引言

旅行商问题（TSP）一般是指找到一条经过给定城市的路线，这条路线长度最短。很多相似的问题都可以用此问题进行建模，同时由NP 完全性理论可知，如果可以用计算机有效地解决此问题，将有助于解决其他NP 完全问题，但经过几十年的努力，还没有发现一种有效解决此类问题的精确算法。

用近似算法解决此类问题，是当前应对此类问题的有效方式，但由于近似算法的设计与问题的形式相关，需要对某一类问题进行深入研究，而根据相关领域知识设计启发式算法，其算法设计难度较大。

机器学习是利用已知经验和数据求解问题的一类算法，使用机器学习方法（特别是神经网络）设计解决组合优化问题的算法已成为当前的研究热点，Bello I 等使用指向性网络（PointerNetwork）和强化学习方法设计了组合优化问题的神经网络求解方法[1]；Bengio Y 等对用神经网络求解组合优化问题进行了综述[2]；Kool W 等使用注意力机制（Attention）对路径问题进行了算法设计[3]；Joshi C K 等使用图神经网络（GNN）对路径问题进行了建模并使用与Kool W 相似的强化学习方法进行了求解[4]。

上述研究指出了设计神经网络求解组合优化问题的方法主要分为三个部分，即设计求解问题的神经网络结构、设计训练该网络的算法以及使用训练算法对神经网络进行训练。本文将基于Transformer 架构[5]（一种基于序列的神经网络架构，适合用作序列建模），配合强化学习算法，设计求解旅行商问题的神经网络。

1 问题描述

旅行商问题（Travel Salesman Problem）：给定一个图G=（V，E），其中，V 是G 的节点集，E 是G的边集，给定一个从E 到R+的代价函数cost，求该图的一条环游C，使得该环游的总代价最小，即使得∑e∈Ccost（e）最小。

如果限制该代价函数，使其满足：当任意三边e1、e2、e3构成一条回路时，有cost（e1）≤cost（e2）+cost（e3）成立，则该问题被称为欧氏旅行商问题。

由NP 完全性理论可知，如果能找到一种有效算法解决欧氏旅行商问题，也就能找到解决一般旅行商问题的有效算法。故以下讨论均限制在欧氏旅行商问题的范围内。

2 注意力模型

2.1 注意力模型的概要描述

在序列到序列的模型中，从源序列生成目标序列时，不仅要考虑当前状态和源序列中的元素，还要考虑当前序列中元素与上下文元素关系的这种方法被称为注意力机制。

注意力机制，即对齐机制，最早出现在神经机器翻译[6]中，这项技术能让解码器在每个时间步长中专注于某些被编码器编码的单词，使得输入单词到翻译结果的路径变短，从而实现减少短期记忆限制影响的目的。

在文献[5]中，研究人员通过Transformer 神经网络架构，显著改善了神经机器翻译的水平；另外，当前最流行的生成语言模型chatGPT 其内部架构GPT-3[7]也是基于此神经网络架构设计的。由于Transformer 架构除了自注意力机制（指当表示序列中某一时刻状态时，可以通过计算该状态与其他时刻状态的相关性，从而生成目标序列中的元素的方法）和一些必要的连接层（如嵌入层、归一化、线性层等）外，不包含卷积层和循环层，故其训练速度比其他完成相似功能的网络有明显提高。

2.2 Transformer 架构

一般情况下，我们将从序列映射到序列的神经网络模型归结为编码器－解码器模型，其含义为将输入I 用神经网络变换为中间表示M，然后将中间表示M 再通过神经网络变换为O。在这一过程中将I 变换为M 的阶段称为编码，由编码器完成；而将M 变换为O 的阶段称为解码，由解码器完成。Transformer 模型中的编码器和解码器均使用了自注意力层和线性层，并以残差方式连接，并进行归一化操作，即每一层的输出xo均为：

其中，Sublayer 函数可以看作自注意力层（多头注意力层）和线性层，LayerNorm 表示归一化函数。Transformer 的核心结构如图1 所示，其中虚线框中的层作为一个整体可根据需求重复多次。值得注意的是，图1 与文献[5]中描述的Transformer结构稍有差别，其表现为图1 去掉了原始的位置编码部分。

图1 Transformer 网络主体架构[5]

在图1 中，嵌入操作是一个线性变换，将输入变为多个特征，可由一个线性层表示；多头注意力（Multi-head Attention）的具体结构在文献[5]中有相关描述，这里总结如下：

计算注意力的方式，可用以下公式表示：

计算多头注意力的方式，用如下公式表示：

其中，headi通过以下公式计算：

以上公式中WQ、WV、WK分别表示以Q、V、K为输入的线性层表示矩阵，Concat 函数表示将headi（i=1...h）合并为一个h×dv维的行向量，该行向量输入以WO表示的线性层将得到多头注意力。

2.3 基于Transformer 架构构建求解欧式旅行商问题的神经网络

在2.2 节中描述了Transformer 架构的核心结构，结合欧式旅行商问题的描述（这里取代价函数为图G 中两点的欧式距离，在求欧氏距离时以每个结点的坐标作为输入，神经网络的输入为图G中结点的位置坐标），设计求解问题的神经网络如图2、图3 所示。

图2 编码器

图2 是编码器部分（虚框中的部分作为整体，重复2 次），即将一个带欧式距离的无向图通过多头注意力层和线性层变换为一个张量（图G 的编码），为解码器提供必要的信息。在编码器中使用多头注意力时，其Q、K、V 均为同一张量，在计算多头注意力时需要依次使用公式（4）、（2）、（3），这里不再重复。

图3 是解码器部分，其作用是将编码器提供的张量与输入一起生成被选择路径上结点的概率分布信息。

图G 中结点概率分布生成后，使用贪心法选择最大概率所对应的结点，这样就完成了一个结点的选择，重复使用图3 所示的神经网络架构，可生成一系列的结点，直到图G 中的结点全部被访问一次，这样就生成了一条回路，计算该回路的总长度，以及生成该回路结点的对数概率分布，作为持续改进回路的激励方式。

3 训练算法

深度强化学习是一种通过激励调整神经网络参数的学习算法，被广泛用于解决智能体的行动问题，如智能体玩电子游戏、下棋等一系列问题。深度强化学习，主要分为基于价值函数的学习方法和基于策略梯度的学习方法，以及这两种学习方法的结合。在这里我们使用带基线的策略梯度学习方法训练求解TSP 问题的神经网络，具体算法可用伪代码描述，见图4。

图4 带可变基线的策略梯度学习算法

该算法中的t 检验是差异显著性检验，在这里通过对比当前参数下计算得到的路径总长度与基线参数下计算得到的路径总长度的差异显著性，来判断是否应当更新当前基线。

4 实验

笔者用以下环境（见表1）对问题实例进行了训练和求解。

表1 训练与求解环境

训练中分别使用了包含10 000 个20 结点TSP 问题实例的数据集、包含10 000 个50 结点TSP 问题实例的数据集以及包含10 000 个100 结点的TSP 问题实例的数据集。

对20 个结点的TSP 问题训练情况如图5 所示。图5a 是训练损失，图5b 是在训练时每批次的平均路径长度，图5c 是在验证集上的平均路径长度（在训练过程中，对于每一个数据集通过随机打乱等方式生成1.28×108个实例，每个batch 由512个实例组成，每训练50 次记录一次数据，总计50 000 条数据，训练时间为4 小时47 分39 秒）。

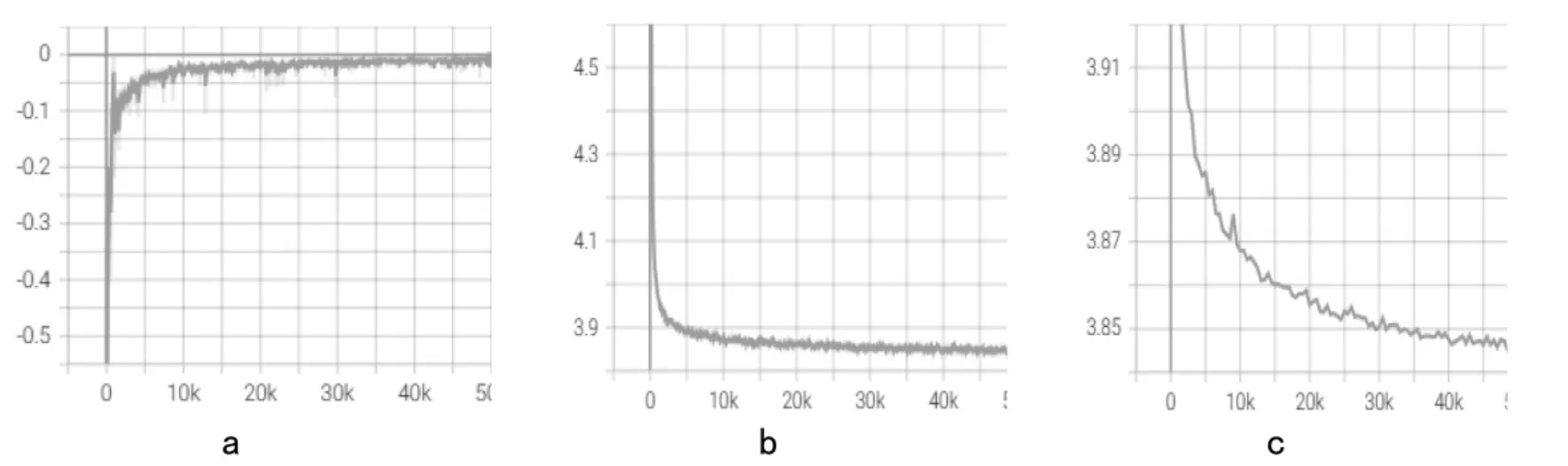
图5 TSP20 数据集上的训练与验证（未平滑）

对50 个结点的TSP 问题训练情况如图6 所示。图6a 是训练损失，图6b 是在训练时每批次的平均路径长度，图6c 是在验证集上的平均路径长度，为看清数据趋势我们对数据进行了平滑处理，其平滑度为0.6（由于显存限制，在50 个结点的TSP 问题训练时，我们将每个batch 的实例数设置为200，其他参数不变，总计128 000 条数据，训练时间为15 小时5 分46 秒）。

图6 TSP50 数据集上的训练与验证（平滑度0.6）

对100 个结点的TSP 问题训练情况如图7 所示。从图中可以看出训练数据与训练损失的关系（见图7a），训练数据与平均路径长度的关系（见图7b），验证数据与平均路径长度的关系（见图7c），平滑度仍取0.6（每个batch 的实例数设置为50，训练时间为53 小时22 分27 秒）。

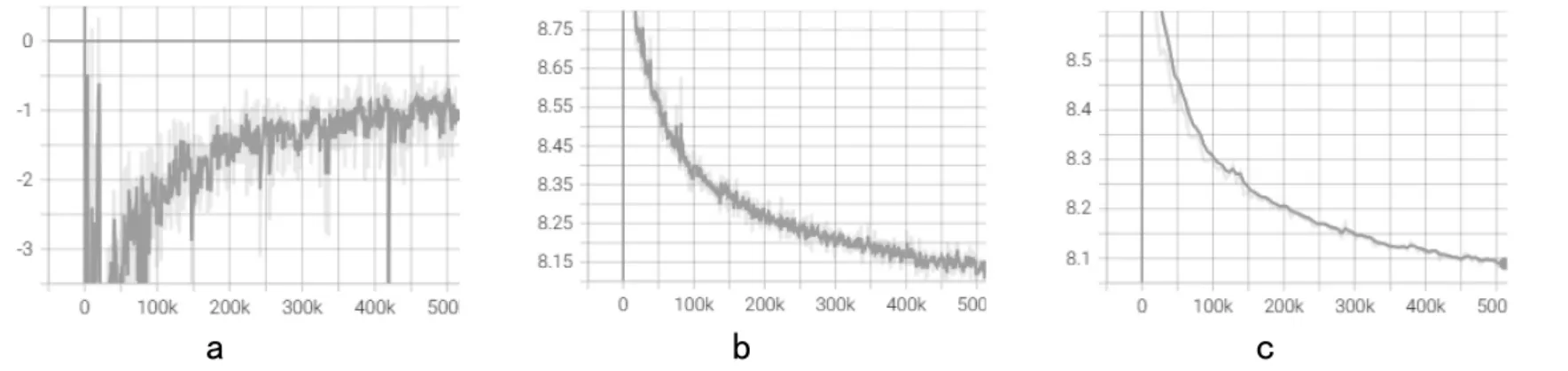
图7 TSP100 数据集上的训练与验证（平滑度0.6）

从平均路径长度和验证时的平均路径长度来看，以Transformer 架构和图4 中所示算法构建求解TSP问题的神经网络模型是可行的，不过训练时间相对较长，随着硬件技术的发展，训练时间会进一步缩短。

5 结语

一旦神经网络训练完成，可以得到关于求解某一规模的TSP 的神经网络，并且可以通过神经网络得出结点的选择概率。此操作的复杂度是问题规模的多项式级别，另外通过选择概率获得路径也是问题规模的多项式级别的操作，故可以认为在获得训练好的神经网络后，求解TSP 是多项式时间可近似的。在寻找近似算法的过程中，笔者没有使用除问题实例外的其他知识，仅使用了较长的计算时间，这种方法为寻找相应问题的近似算法提供了一定的思路。

使用这种方法求解TSP 也有一定的缺点，主要表现在求解问题的神经网络的训练时间相对较长。如何缩短训练时间是后续研究的主要方向，一方面可以从改进训练算法的角度考虑；另一方面可以从引入量子算法对神经网络架构和训练算法的角度进行改进，以便使用量子计算机求解相应问题。