具有无症状感染者和时滞的媒介传染病模型的分析

闫娟娟, 雒志学, 高文哲

(兰州交通大学数理学院, 兰州 730070)

传染病严重危害人类的健康,如登革热,霍乱等给人类的生存带来了巨大的灾难.众所周知,疾病发展的过程中,了解传染率至为关键,目前已有大量学者建立了具有双线性发生率和标准发生率的传染病模型.在现实生活中,传染病一般会有潜伏期,当易感者与染病者接触感染后,先是携带病毒,但病毒不会立即爆发,而是经过一段时间才发病成为染病者,这一过程在数学模型中通常用时滞来表示.文献[1]对具有双线性发生率的时滞传染病模型进行了分析,对平衡点进行了讨论,证明了满足某些条件时时滞可以导致Hopf分支的产生,并讨论了分支的性质.随着染病者行为的变化,发生率会趋近于饱和状态,因此采用饱和发生率更加符合实际.文献[2]研究了具有饱和发生率的媒介传染病模型,文献[3-9]对具有饱和发生率和潜伏期时滞的传染病模型进行了分析,讨论了在一定条件下平衡点的稳定性,间接说明时滞也许不会给疾病的传播带来影响.文献[10]研究了具有饱和发生率和免疫期时滞的传染病模型,给出了平衡点全局稳定性的条件,证明了时滞可以导致地方病平衡点的稳定性发生变化从而在该平衡点存在Hopf分支.在文献[11-13]中,学者对具有时滞的媒介传染病模型进行了研究.无症状感染者由于没有明显的特征而被忽略,从而低估疫情爆发的风险.上述模型均没有考虑无症状感染者.本文在文献[2]的基础上讨论了一类具有无症状感染者和时滞影响的媒介传染病模型．

1 模型的建立

在文献[2]的基础上本文建立如下具有时滞的媒介传染病模型:

(1)

其中,Sh(t)、Ia(t)、Ib(t)、Rh(t)分别表示人群中的易感者,无症状的感染者,有症状的感染者,恢复者.Sv(t)、Iv(t)分别表示易感媒介,染病媒介.Λh,Λv分别表示人群和媒介的补充率,β1表示染病媒介对易感人群的感染率,β2表示染病人群对易感媒介的感染率,μh表示人群中的自然死亡率,μv表示媒介的自然死亡率,γa表示无症状感染者的恢复率,γb表示有症状感染者的恢复率,da表示无症状感染者的因病死亡率,db表示有症状感染者的因病死亡率,αi(i=1,2,3)表示饱和发生率,p表示无症状感染者向易感媒介传播疾病的概率,θ表示易感者与染病媒介所接触成为无症状感染者的概率,τ为时滞,表示疾病的潜伏期.

模型的初始条件满足:

Sh(θ)=φ1(θ),Ia(θ)=φ2(θ),

Ib(θ)=φ3(θ),Iv(θ)=φ4(θ),φi(θ)>0,φi(0)>0(i=1,2,3,4),θ∈[-τ,0].

(2)

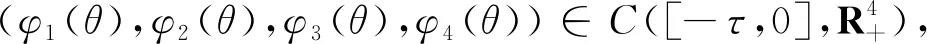
(3)

下面证明Ω是系统(3)的正向不变集．

引理1设(Sh(t),Ia(t),Ib(t),Iv(t))是系统(3)满足初值条件(2)的解,当t≥0时,(Sh(t),Ia(t),Ib(t),Iv(t))是有界的．

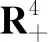
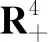
2 平衡点的存在性和基本再生数

R0=

k1=μh+γa+da,k2=μh+γb+db.

(4)

其中,

3 稳定性分析

3.1 平衡点E0的稳定性分析

局部稳定性的证明类似于文献[14]中的证明,因此得到如下定理．

定理2当R0<1且τ≥0时,平衡点E0是局部渐近稳定的;当R0>1时,E0是不稳定的．

定理3当R0<1时,系统(3)的平衡点E0是全局渐近稳定的．

证明构造Lyapunov函数

V=Z1Ia+Z2Ib+Iv+

其中,

k1=μh+γa+da,k2=μh+γb+db,

则V关于系统(3)的导数为

3.2 平衡点E*的稳定性分析及Hopf分支存在的条件

定理4当R0>1时,平衡点E*是局部渐近稳定的．

证明系统(3)在平衡点E*处所对应的特征方程为

λ4+c1λ3+c2λ2+c3λ+

(d1λ2+d2λ+d3)e-λτ+c4=0,

(5)

其中,

c1=h1+k1+k2+h2,c2=k2h2+k1k2+k1h2+h1k2+h1h2+h1k1,c3=h1k2h2+k1k2h2+h1k1k2+h1k1h2,c4=h1k1k2h2,d1=cm2+m1b,d2=cm2k1+cm2h1-adm1-aem2+(h1+k2)m1b,d3=h1cm2k1+h1m1bk2-adm1k2-aem2k1,

其中,

k1=μh+γa+da,k2=μh+γb+db,

1) 当τ=0时,方程(5)变为

λ4+c1λ3+(c2+d1)λ2+(c3+d2)λ+

d3+c4=0.

(6)

根据Hurwitz判别法,(6)式的每一个根均有负实部,因此,当R0>1且τ=0时,系统(3)的平衡点E*局部渐近稳定．

2) 当τ>0时,设λ=iω(ω>0)是方程(5)的一个纯虚根,分离实部与虚部得

(7)

将(7)式的两个方程分别平方后再相加得

ω8+B1ω6+B2ω4+B3ω2+B4=0,

(8)

其中,

(9)

令w2=y,则方程(8)变为

y4+B1y3+B2y2+B3y+B4=0.

(10)

定义

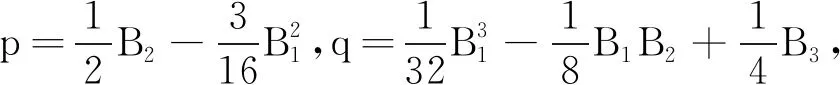
根据文献[15]中根的分布可以得到方程(10)的根有以下结论.

1) 若B4<0,则方程(10)必有一个正实根．

2) 若Δ≥0,B4≥0,当且仅当y1>0,h(y1)<0时,方程(10)存在正实根．

3) 若Δ<0,B4≥0,当且仅当存在一个y*∈(y1,y2,y3),使得y*>0,h(y*)≤0,则方程(10)至少存在一个正实根．

其中,

当τ=τ0、λ=iω0时,可以得到

其中,

d2,

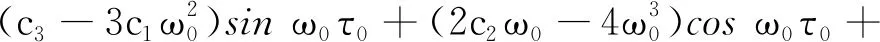
2d1ω0,

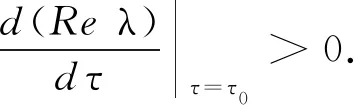
综上所述,可以得到如下定理.

定理5当R0>1且β1V1+β2V2≠0时,

1) 当τ∈[0,τ0)时,系统(3)的地方病平衡点是局部渐近稳定的;

2) 当τ>τ0时,系统(3)的地方病平衡点是不稳定的;

3) 当τ=τ0时,系统(3)在地方病平衡点E*处产生Hopf分支．

4 Hopf分支方向和周期解的稳定性

4.1 建立抽象微分方程

如果τ=μ+τ0,则在μ=0处,系统(3)将会在地方病平衡点E*处产生Hopf分支,即μ=0为系统(3)产生Hopf分支的分支值．

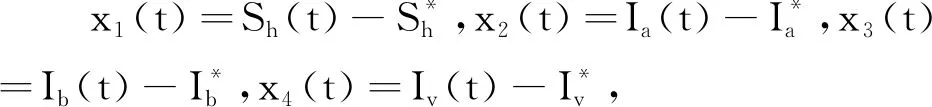
x′(t)=Lμxt+f(μ,xt),

(11)

其中,x(t)=(x1(t),x2(t),x3(t),x4(t))T∈R4,Lμ:D→D4,f:R×D→R4.

当φ=(φ1,φ2,φ3,φ4)∈D([-1,0],R4)时,有

Lμ(φ)=

(12)

其中,

(13)

其中,

由Riesz表示定理可知,存在一个有界变差函数η(θ,μ),θ∈[-1,0],使得

(14)

事实上,可以令

(15)

其中,

对于φ∈C([-1,0],R4),定义

则系统(11)转化为

x′(t)=Aμxt+Rμxt,

(16)

其中,xt(θ)=(x1(t+θ),x2(t+θ),x3(t+θ),x4(t+θ)),θ∈[-1,0]．

4.2 Hopf分支的方向和稳定性

对于φ∈C([-1,0],R4),定义A的伴随算子A*如下,

对于φ,φ∈C,定义双线性内积为

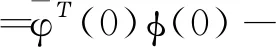
(17)

其中,η(θ)=η(θ,0),A(0)与A*是一对共轭算子.±iω0τ0是A(0)的特征根,则它也是A*的特征根,下面计算A(0)关于特征根iω0τ0的特征向量以及A*关于特征值-iω0τ0的特征向量．

假设p(θ)=(1,p1(0),p2(0),p3(0))Teiω0τ0θ是A(0)关于特征值iω0τ0的特征向量,于是有A(0)p(θ)=iω0τ0p(θ),计算可得

由(17)式得

〈p*(s),p(θ)〉=

(1,p1,p2,p3)Teiω0τ0ξdξ=

为了确保〈p*(s),p(θ)〉=1,令

根据文献[16]中Hassard提出的方法可以得到一些重要的系数:

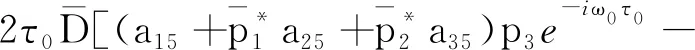
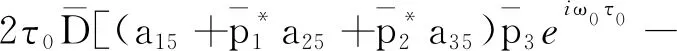
其中,

(18)

下面求B1,B2,当θ=0时,有

(19)

因此有

K11(0)=

(20)

将(18)式的第一个式子和(20)式的第一个式子代入(19)式的第一个式子得

等价于

同理将(18)式的第二个式子和(20)式的第二个式子代入(19)式的第二个式子得:

求出B1、B2的值后可分别代入W20(θ),W11(θ)的表达式中,进一步也可以算出g21.因此可以算出下列表达式的值:

(21)

综上所述得到以下定理.

定理6当τ=τ0时,分支周期解的性质由(21)的各个表达式决定,因而得到以下3个结论.

1) Hopf分支的方向由μ2的符号决定,若μ2>0(μ2<0),则Hopf分支是超临界的(亚临界的)．

2) 分支周期解的稳定性由β2的符号决定,若β2<0(β2>0),分支周期解是稳定的(不稳定的)．

3) 分支周期解的大小由T2的符号决定,若T2>0(T2<0),分支周期解的周期增大(减小)．

5 结论

本文是在文献[2]的基础上,同时考虑无症状感染者和潜伏期时滞的媒介传染病模型.通过分析得到以下结论:1) 当τ≥0且R0<1时,平衡点E0是全局渐近稳定的,疾病不再存在.当R0>1且τ=0时,平衡点e*是局部渐近稳定的;2) 当R0>1且0≤τ<τ0时,平衡点e*局部渐近稳定,τ>τ0地方病平衡点不稳定;3) 当R0>1且时滞τ经过临界值τ0时,地方病平衡点的稳定性丧失,从而这个平衡点处出现Hopf分支,利用Hassard等[16]提出的规范型理论和中心流形定理分析了分支方向和周期解的稳定性.这种媒介传染病模型的研究,对预防和控制此类传染病有着非常重要的作用．