基于公交车开展物流配送的车辆路径优化问题

颜梦铃

（重庆交通大学经济与管理学院，重庆 400074）

0 引言

如今，电子商务增长、生活节奏加快、共享型经济兴起及可持续发展等趋势，不断驱动着城市物流配送的发展和变化。日益频繁的货物需求导致城市中心每天有大量的商品流通，这使得城市配送必然是多品种、小批量、高频次的，而客户对配送时效性以及反应速度的要求也越来越高。许多企业推出了一系列时效性服务产品以满足不同场景下不同消费者对物流速度的不同需求，这使得客户能够在精确的时间段内收取货物，可见城市配送的及时性和精确性已成为物流服务的重要指标。

客货共运系统现已在国外得到了初步应用。MARINOV 研究了欧洲各国相关案例：2003年，德国德累斯顿开始利用轨道交通为大众公司提供货运服务，2007年，荷兰阿姆斯特丹开始尝试采用有轨电车运输货物，同期，法国巴黎开始借助客运列车实现市中心与市郊之间的货物运输[1]。KIKUTA 研究了日本札幌市于2010年开展的地铁配送货物的试验[2]。目前，我国正积极推动客货共运系统的研究和建设。2022年省交通运输厅联合省财政厅印发了《吉林省开展客货场站客货一体化转型升级改造2021-2022年度专项补助资金实施方案》，对客运企业实施公交化改造、全域公交等方面进行补助。充分发挥载运工具和基础设施的富余能力，实现客货共运，将成为未来交通发展的重要趋势[3]。

客货共运模式可以分为两类，一个是“点－干线－点”运输模式，另一个是“点对点”配送模式。“点－干线－点”运输模式中，公交车/轨道交通承担货运中转站之间的中长距离“干线”运输工作，物流配送企业承担快递收集及末端配送等“点”端业务[4]。Nash[5]最早提出了使用公共交通工具运送货物的概念。Trentini 等[6]提出旅客、货物共同使用交通资源，共享道路容量、公共交通服务及基础设施。包括共享公共汽车、地铁、电车；共享多用途车道、货车车道；共享配送站、停车场货物柜、地铁站储物柜等[7，8]。Fatnassi 等[9]提出了客流和货流共享快速运输网络，研究了整合乘客快运和货物快运（PRT-FRT）模式，以估计在城市地区整合共享交通模式的潜力及其提高可持续性的能力。Bi 等[10]分析了高铁快递对高铁网络的适应性，并计算了高铁快递包裹在高铁网络的运输量。Behiri 等[11]后来对城市地铁网进行货运做了进一步的研究，开发了一种鲁棒蚁群优化（ACO）元启发式算法来处理大型实例。而“点对点”配送模式以出租车作为主要的配送载体，实现货物点到点的运输，该模式适用于高附加值、时效性要求高的货物运输。AMOUS 等[12]建立了一个实时匹配司机和乘客的动态合乘模型；Li 等[13-15]将乘客和包裹整合在同一出租车网络，详细定义共享问题（share-a-ride），确定最佳时间表和路径。

通过对客货共运相关问题的研究发现，现有的文献多以地铁货物相关问题为主，较少涉及公交车货运。而且大多集中在对模式的可行性分析、风险控制、“最后一公里”的客货共运等问题的研究上，较少讨论在公交中客货协同的车辆路径问题。所以，本文将以公交车的动态客流量为基础，探讨以公交车为载体的客货协同问题。

1 基于公交车开展物流配送的路径优化模型建立及算法设计

1.1 基于公交车开展物流配送的路径优化问题具体描述 基于公交车开展物流配送的路径优化问题描述为货物从配送中心由公交车转运至一个公交站点，然后用配送车辆从公交站点配送至物流中转站进行简单的分拣再配送给客户，最后配送车辆返回物流中转站的过程。由于本文提到的配送中心临近公交站点，故将该公交站点作为虚拟的配送中心进行探讨。且配送车辆提前至末端公交站点等候，货物到站后直装车配送至物流中转站进行分拣，送往下一级客户[16]。模型假设如下：①不考虑公交站的储存功能，货物到站后直接装车配送；②配送中心到公交始发站的距离忽略不计。本文以总成本U 最小化为目标，其中包括固定成本，运输成本和转运成本，符号定义如下：J={1，2，3，…，j}表示客户点集合；V={1，2，3，…，v}表示车辆集合；p 表示物流中转站；K={1，2，3，…，k}表示公交站点集合；dih表示节点i 和h 之间的距离；θ 表示公交车转运货物的单位转运成本系数；qj表示客户j 的需求量；表示公交车b 在公交站点k 时的剩余运能；Qv表示配送车辆v的容量限制；mv表示配送车辆v 的单位成本；Nbk表示公交车b 在公交站k 时的乘客数；表示公交车r 在公交站点k 上车的乘客数量；表示公交车r 在公交站点k 下车的乘客数量；表示配送车辆v 从节点i 行驶到节点h，取值为1，否则为0；表示公交车b 在公交站点能够转载的货物量满足预定的最小值取值为1，否则为0。

以物流总成本最小化为优化目标，建立基于公交车开展物流配送的路径优化模型如下：

其中式（1）表示物流总成本最小化；式（2）表示每个客户只能被访问1 次；式（3）表示从物流中转出发的配送车辆一定回到物流中转站；式（4）表示配送车辆的负载限制；式（5）表示公交的运能能满足其所分配的客户需求；式（6）表示当公交车r 从公交站点k 出发时车上乘客的数量，即公交车r 从公交站点k-1 出发时车上乘客数加上在公交站点k 增加的乘客数；式（7）表示公交车r 能够装载的货物量，即线路l 中的公交车r，在所有公交站点中能够装载的最小货物量；式（8）-式（9）表示决策变量的0-1 约束。

1.2 改进遗传算法 本文基于公交车开展物流配送的车辆路径优化模型为单目标模型，对于该类模型的求解，通常使用启发式算法，例如蚁群算法、变邻域搜索算法、模拟退火、遗传算法、禁忌搜索等。本文对遗传算法（GA）生成的种群个部分染色体采用模拟退火算法（SA）进行优化拓展解的空间，提高算法的全局和局部空间搜索能力。首先，随机生成初始解产生初始种群并计算适应度函数值，接着用模拟退火算法优化部分经过交叉、变异、选择后的染色体，最后应用GA 算法进行配送方案优化，进而生成配送路径。算法的流程图如图1 所示。

图1 改进的遗传算法流程图

①染色体的编码与解码。该算法的染色体采用正整数编码方式，长度为需要配送的顾客点和车辆数之和，每条染色体代表一个可行解。若需用V 辆车服务N 个顾客点，则全部顾客序号1，2，…，N、全部车辆序号为N，N+1，……，N+V 构成染色体的N+V 个基因，0 表示物流中转站，每个基因的值对应一位顾客或者车辆的序号。如N=5、V=7，某染色体为{1，2，3，6，4，5，7}，表示一个顾客点总数为5、车辆数为2 的可行解，其中的数字代表相应顾客点和车辆序号，路径1：0→1→2→0；路径2：0→3→4→5→0。代表第一辆车从物流中转站出发依次服务顾客点1、2 后返回物流中转站，第二辆车从物流中转站出发依次服务顾客点3、4、5 后返回物流中转站。

②选择。本文的改进算法中使用的是轮盘赌法。首先通过个体的适应度值计算每个个体的被选择概率P，如式（10）所示，为个体i 的适应度值。然后将每个个体的选择概率进行累积求和生成一个累积概率表。最后生成一个0到1 之间的随机数，根据随机数在累积概率表中的对应位置，找出对应个体作为选择结果。

③变异。对染色体中每一位基因进行以下操作：1）随机一个浮点数r；2）比较r 与变异pm，若r 较小，则对当前基因为进行变异，变异为取值域内一个随机数，否则进行下一位基因的操作。

④交叉。本文采用的是两点交叉。即在父代染色体中随机设置了两个交叉点，然后再进行部分基因交换。例如有父代染色体 1 {1，2，3，6，4，5，7}、 染色体 2{1，2，6，3，4，7，5}，两个交叉位点是第2 个和第5 个。那么就将染色体1 中的{2，3，6，4}与染色体2 中的{2，6，3，4}交换位置，得到两个子代染色体 {1，2，6，3，4，5，7}和{1，2，3，6，4，5，7}。

⑤模拟退火算法。模拟退火算法是一种新的随机搜索方法，它是近年来提出的一种适合于解决大规模组合优化问题的通用而有效的近似算法。与以往的近似算法相比，模拟退火算法具有描述简单、使用灵活、运用广泛、运行效率高和较少受到初始条件约束等优点。模拟退火算法包含两个部分即Metropolis 算法和退火过程。退火过程是一种贪婪的方法，其目标是要找到最大值。而Metropolis 算法是以一定的概率来接受新解，从而避免陷入局部最优的情况。

2 算例分析

2.1 算例验证

为了验证模型和算法的有效性，本文以重庆市主城区某配送中心（DC）、20 个（客户点C1-C20）以及选取的303路公交车，其中2 个公交站点四公里（K1）、龙洲大道（K2）2 个与之对应的物流中转站（P1、P2）参与货运。假设客户需求在10-20 间随机分布，地理位置服从均匀分布，可通过高德地图获取坐标及其之间距离。公交系统运送货物的单位成本为3 元，配送车辆的单位运输费用为10 元，配送车辆的维修成本为50 元/辆，物流中转站的固定成本为50元，违反时间窗的单位时间惩罚成本是15 元/时。

2.2 结果分析

优化前没有公交车参与货运，由货车单独完成配送任务。虽然没有转运成本，但是配送成本较高，进而导致物流运用总成本较大。针对基于公交车开展物流配送的车辆路径优化问题，以总成本最小化为目标函数，应用改进的遗传算法对优化模型进行求解，得到基于公交车开展物流配送的车辆路径优化前后总成本、配送车辆使用数以及运输时间等变化情况如表2 所示。

表1 基于公交车开展物流配送的车辆路径优化方案表

表2 基于公交车开展物流配送的车辆路径优化前后对比

由表2 和图2 可知，通过公交车开展物流配送，配送车辆减少了3 辆，公交转载率提高至50%，将部分货运任务转移给了公交车；总成本减少了30%，其中转运成本增加了300 元，固定成本减少了25.67%，配送成本下降了51.86%；运输时间减少了41.7%。

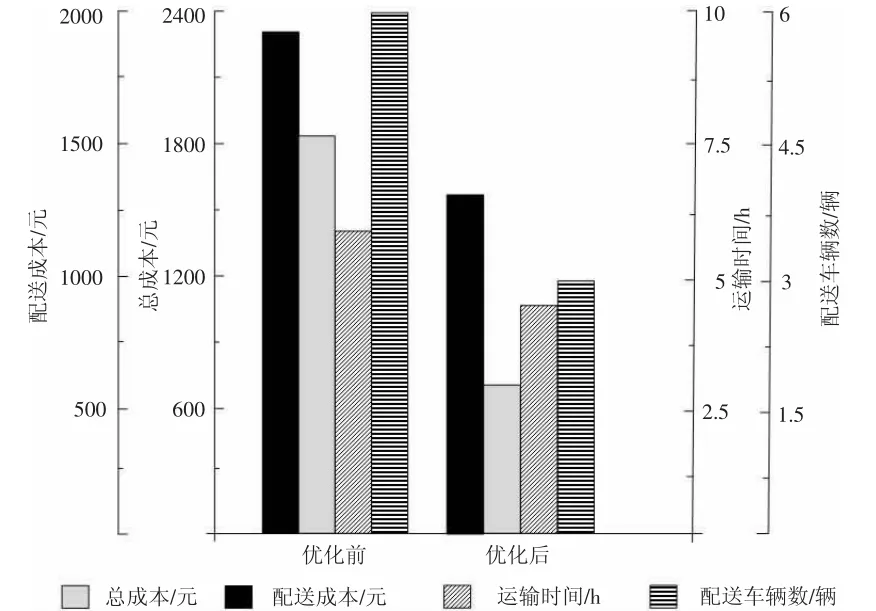
图2 路径优化前后对比各项指标对比图

3 结论

本文从公交车货运出发，构建了物流配送车辆路径问题提，以最小化成本为总目标，构建城市物流路径优化模型。运用改进的遗传算法求解该模型，该算法在遗传算法生成种群的过程中，运用模拟退火算法进行优化拓展解的空间。本文以重交市某区域公交站点为例，对比分析了基于公交车开展物流配送的车辆路径优化前后总成本和运输时间等的变化情况，获得了物流配送的最优路径结果，节约了配送成本，验证了改进后算法的有效性。