热-湿-应力耦合作用下框架锚杆支撑的边坡冻融特性分析
2023-12-14刘铭鲍硕超
刘铭, 鲍硕超
(吉林建筑大学土木工程学院, 长春 130000)
冻土区的存在及其演变过程诱发的热融滑坡[1]对自然环境和人类生产活动造成了不同程度的影响,直接威胁人民的生命财产安全,与边坡稳定性密切相关的是边坡防护工程。传统的支护结构在冻土边坡治理中存在诸多问题,如部分防护结构在冻胀作用下破坏,无法达到理想的防护效果。因此,对冻土边坡防护需要一种安全有效、技术先进、施工方便、造价经济的方法[2]。
对于冻土区边坡防治问题,许多学者在冻土边坡的理论与防治措施方面进行了大量研究。Zhang等[3]研究发现,冻融破坏是冻土区边坡失稳的最主要原因,其本质是土壤水分在土壤孔隙中的冻结和融化。Xin等[4]针对不同土质进行试验发现,不同性质的土体经历冻融循环后其强度变化也不同,土体黏聚力和摩擦角随着干密度、冻融循环和饱和度的增加而逐渐减少。Abdolghanizadeh等[5]提出冻融循环次数增加导致土体产生的非线性应力松弛,是边坡稳定性研究的重要部分。Vahdani等[6]在对冻融数值模型的研究中,将温度作为一个额外的变量,引入一个广义的应变和应力张量,以此来计算对边坡稳定性的影响。
近年来,学者们针对边坡的支护展开了大量研究。何江飞等[7]针对黄土高边坡治理加固中的空间受限和高填方填筑等问题,提出了加筋土-框锚组合体系,对该组合体系协同作用进行了分析。曹程明等[8]以特殊土岩组合地层为背景,采用桩锚支护,结合监测数据对支护结构内力变化规律进行研究。在众多支护结构中,框锚结构因其简单可靠的设计原理和低廉的造价得到了广泛的发展与应用[9-10]。基于此,以框架锚杆结构支护边坡,设计室外试验。在理论上建立冻融荷载作用下边坡土体的物理场数值计算模型,土体和结构之间工作作用的计算模型。基于模型方程,使用MATLAB编制计算程序,通过与试验结果的对比,验证程序的正确性。得到季冻区框锚支护边坡的水分场、温度场、应力场以及锚杆内力分布规律,揭示支护结构和土体相互作用的机理,为框架锚杆结构支护冻土区边坡的应用提供可靠的理论依据。
1 数学模型
1.1 基本假定
(1)土体土质均匀联系,为各向同性弹性体。
(2)水汽蒸发的耗热量忽略不计,且不计其他化学势和场的作用,如盐分的析出。
(3)不考虑施工时对支护结构造成的误差,假定其一直处于正常工作情况。
1.2 基本方程
根据多孔材料传热传质理论[11],土体冻融过程中温度与水分的变化归结为以下二维方程组[式(1)~式(3)]。
(1)
(2)
ψ=P+G
(3)
式中:C为土体密度ρ和土体比热容cp乘积,即ρcp;t为计算时间;λ为土体的导热系数;θi为体积含冰率;θu为体积未冻水率;ρi和ρw分别为冰和水的密度;kw为与未冻水相关的渗透系数;ψ为土水势能,水压力P和重力势G之和。
水压力P可通过Clapeyron方程[12]描述为
(4)
式(4)中:T0为土体冻结温度;L为冰水相变潜热。
由平衡微分方程和几何方程可得
(5)
式(5)中:∇为拉普拉斯算子;σ为应力矩阵;G为体积力;ε为总应变矩阵;u为位移矩阵。
在冻结过程中,土体体积变化是由原土体中部分水和迁移来的部分水冻结成冰引起的。在冻结和融化过程中假定土体颗粒不可压缩,体膨胀变形εv可表示为
εv=0.09(θ0-θu)+1.09Δθ-n
(6)
σ=c(ε-ε0)
(7)
1.3 结构与土体协调作用
将框架柱等效为梁单元,锚杆等效为杆单元,土体单元采用三角形单元。为保证结构精细化模拟的有效性,至关重要的是单元形成的数值模型的准确与否。因此,采用零厚度四节点单元作为结构和土体的联结单元[13]。如图1所示,联结单元宽度w=0,节点1和4、3和2在开始时占有同一空间位置,可以很方便地放置于结构和土体之间,不影响结构和土体的单元划分。
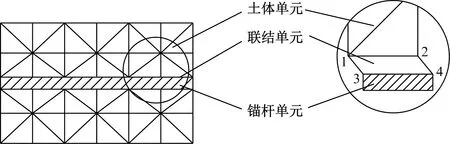
1、2、3、4为联结单元的4个节点序号
联结单元中上层节点1、2与土体单元联结,将土体单元的位移和应力状态传递给下层节点3、4,下层节点再传递给结构单元。通过联结单元的形状函数来描述结构和土体的运动关系,进而体现出二者的联结关系。
1.4 结构与土体协调作用方程
土体为三角形单元,其位移模式[14]为
(8)
式(8)中:ui、uj、um、vi、vj和vm分别为三角单元3个节点i、j、m上x、y方向的位移;NS为土体单元的形函数矩阵;δeS为土体单元的节点位移。
由虚功原理可得到土体单元的刚度矩阵和节点力与节点位移的关系可表示为
(9)
feS=kSδeS
(10)
(11)
(12)
(13)
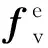
对联结单元其位移可表示为
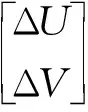
=NBδeB
(14)
式(14)中:ΔU、ΔV为联结单元在x、y方向上的位移;Uup、Udown、Vup和Vdown分布为单元上下边界的在x、y方向上的位移;NB为联结单元的形函数矩阵;δeB为联结单元的节点位移。
由虚功原理可得到联结单元的刚度矩阵和节点力与节点位移的关系可表示为
(15)
feB=kBδeB
(16)
式中:Ω为单元计算空间;kB为联结单元的刚度矩阵;k′为联结单元的刚度系数;feB为联结单元的节点力。
通过对应力场求解得出δeS和feS,即求得联结单元上层节点位移和节点力,代入式(16)即可求得下层节点位移和节点力即δeB,即与结构单元相对应的节点位移,将其代入结构单元中进行计算即可求得结构的节点力。
feStr=kStrδeB
(17)
式(17)中:feStr为结构单元的节点力;kStr为结构单元的刚度矩阵。
将各部分的单元刚度矩阵在整体坐标系下进行迭加可得到结构与土体的整体协调作用方程为
(18)
(19)
(20)
FS=KSδS
(21)
FB=KBδB
(22)
δB=δStr
(23)
FStr=KStrδStr
(24)

由式(1)、式(2)和式(18)~式(24)组成了季冻区框架锚杆支护边坡的水热力耦合模型。
2 建立数值模型
对水分场和温度场采用有限差分法计算得到每个时间步长的结果,对应力场在每个时间步长内采用有限元法进行分析。前文已经给出应力场的有限元方程,不再赘述。仅对温度场的差分公式进行离散分析,在对水分场离散时亦是同理。
2.1 有限差分法
有限差分法[15]是以差分的原理为基础的计算方法,通过离散的函数值所构成的差商来近似逼近相应的偏导数。如温度T对时间t的导数可表示为
(25)
式(25)中:Tn+1为n+1时刻的温度;Tn为n时刻的温度;tn+1和tn分别为n+1时刻和n时刻;Δt为计算的时间步长。
在几何意义上表示求弧线的斜率,如图2所示。
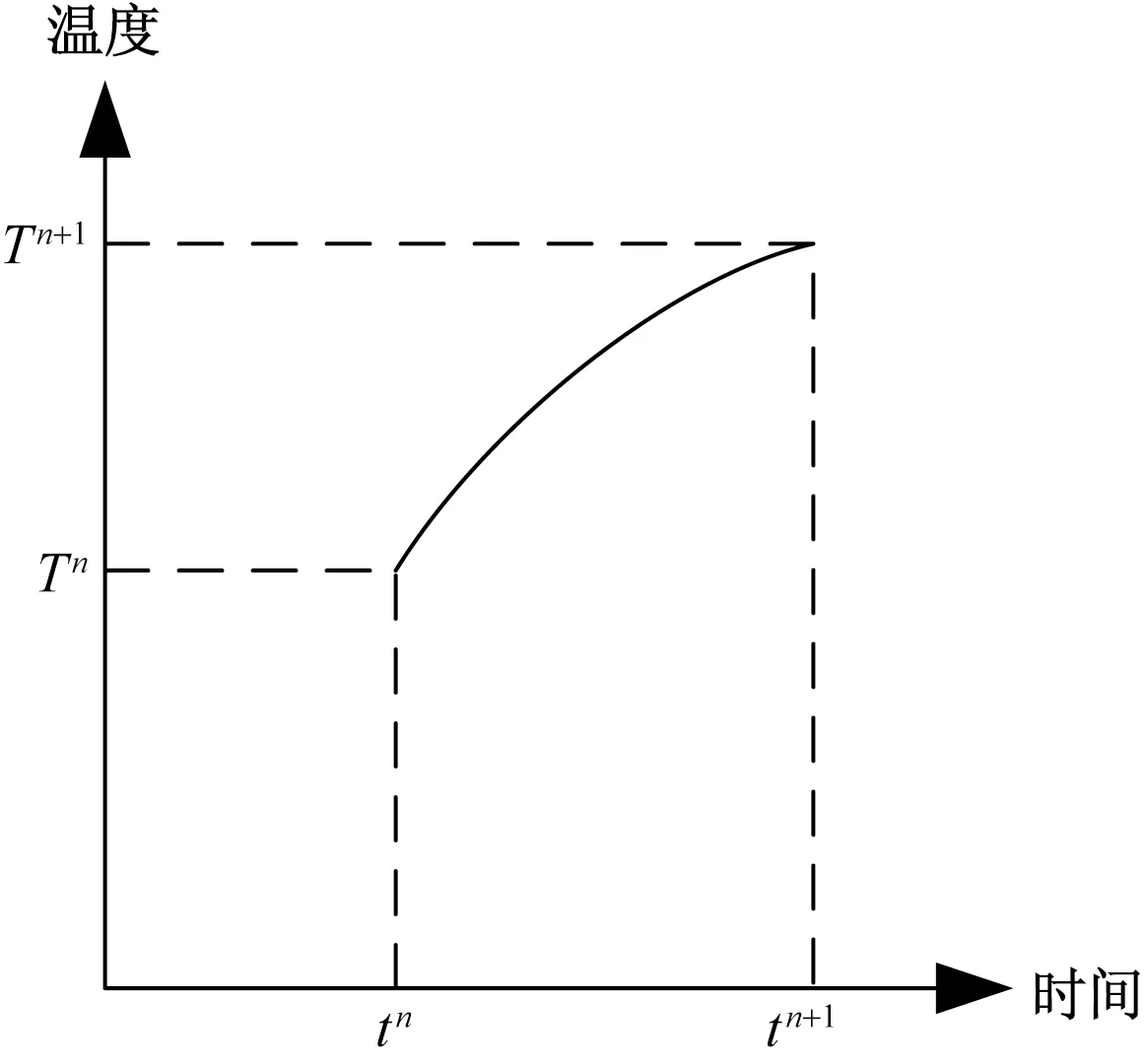
图2 斜率的表示Fig.2 Representation of slope
2.2 建立差分方程
将式(2)~式(4)代入式(1)整理得
(26)
(27)
(28)
为方便理解,在此引入半线。即在点(i,j)和点(i+1,j+1)之间引入点(i+1/2,j)和(i,j+1/2)。式(26)左端中在点(i,j)处T对t的一阶偏导等于点(i,j)在n+1时刻时T和n时刻T的差除以时间步长Δt。即
(29)
(30)
式(26)右端中在n时刻点(i+1/2,j)处T对x的一阶偏导等于n时刻时点(i+1,j)T值和点(i,j)T的差除以空间步长Δx。即
(31)
(32)
n时刻点(i,j)处T对x的二阶偏导等于n时刻时点(i+1/2,j)一阶偏导和点(i-1/2,j)一阶偏导的差除步长Δx。即
(33)
T对y的二阶偏导同理展开即可。
假设在n时刻时,点(i,j)的温度T已知。对式(26)展开后左端有两个时间层n+1、n,右端若都以n时刻展开计算求得的n+1时刻结果误差极大,而都以n+1时刻计算对计算机内存需求增大,变得烦琐。因此,采用交替计算方法即能解决误差又能使计算过程简化。
在n时刻,各点温度值已知,如图3所示。
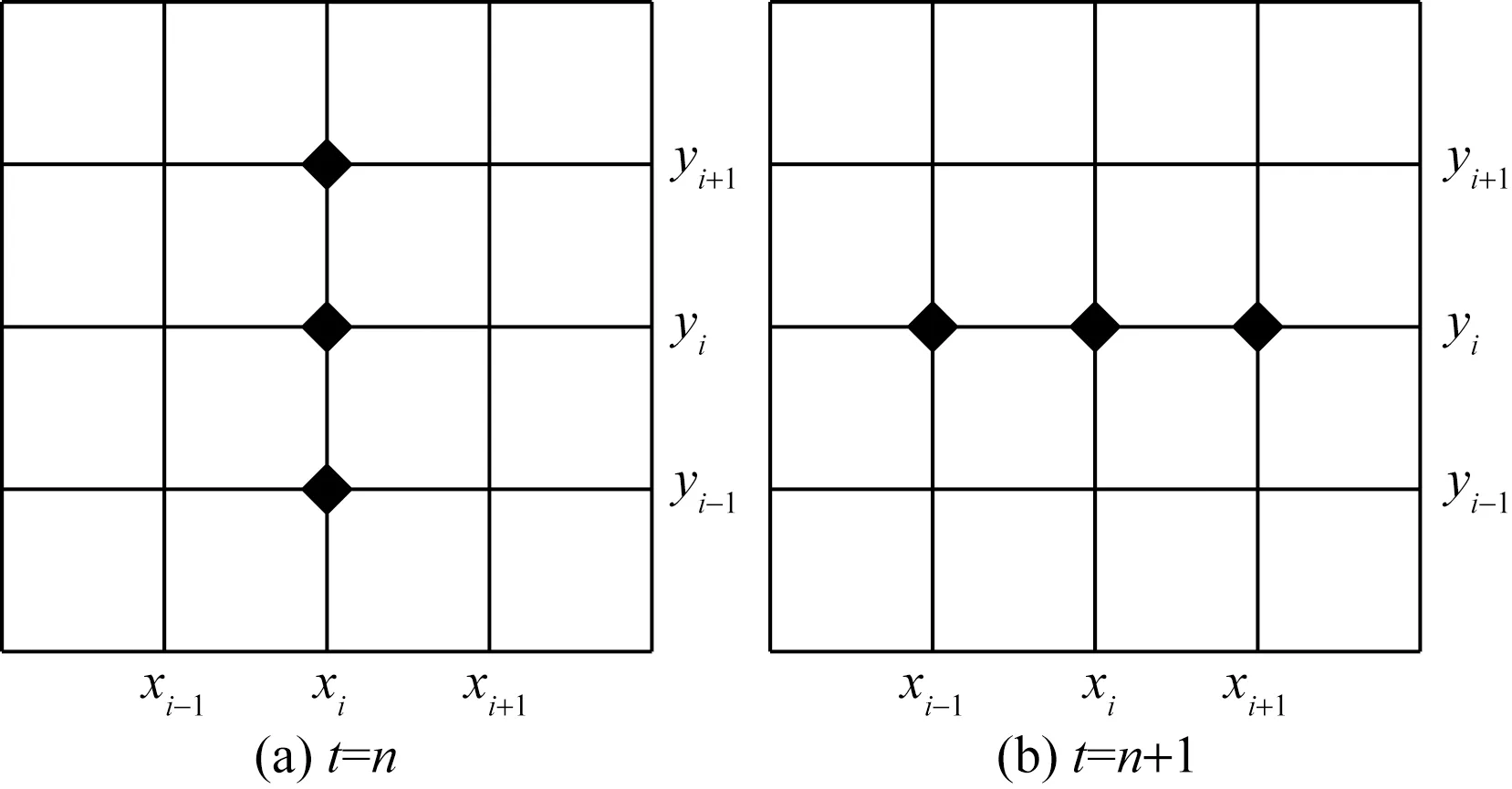
xi-1、xi、xi+1、yi-1、yi、yi+1为n时刻或n+1时刻时,网格单元划分后的坐标
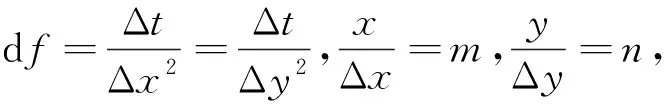
(34)
对于边界条件,在上边界是T关于时间t的函数,即T=T(t);在下边界T为一个已知值。左右边界的热流密度为0,即
(35)
由左边界条件可知:
(36)
对左边界点展开,即i=1时。如图4所示,得到左边界点的差分方程,右边界点同理展开即可。

图4 左边界节点Fig.4 Left boundary node
(37)
对所有离散点都进行如上展开,即在n+1时刻在x方向上展开,在n时刻在y方向上展开。而n时刻时各点T已知,结合边界条件写成矩阵形式为
AU=B
(38)
(39)
(40)
(41)
(42)
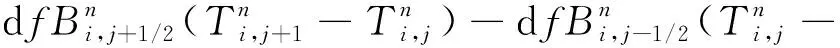
(43)
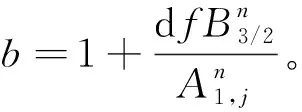
对矩阵方程求解可得到n+1时刻沿x方向展开的离散点T值。
与计算n+1时刻类似,在n+2时刻,此时n+1时刻各点T值已求得。对内部点在y方向上以n+2时刻展开,在x方向上以n+1时刻展开,即能得到n+2时刻的差分方程。不同的是在n+2时刻对边界的处理。
由上边界条件可知,在n+2时刻时上边界点的温度已知,即j=1时。如图5所示,得到上边界点的差分方程,下边界点同理。
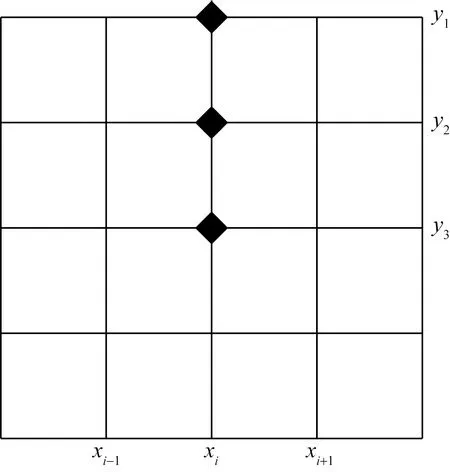
图5 上边界节点Fig.5 Upper boundary node
(44)
在n+2时刻,对离散点都进行相应的展开后组合成矩阵,求得n+2时刻的解。如此反复,便可得到所有时间步长内的解。
3 程序验证
为了得到真实环境下各物理场变化关系,结合室外环境设计了室外试验,将其结果与计算结果进行对比验证。
3.1 室外试验
试验模型坡高3.0 m,坡角为75°,如图6所示。框架混凝土强度等级为C30,横梁尺寸为20 mm(长)×20 mm(宽)×3.0 m(高),立柱尺寸为20 mm(长)×20 mm(宽)×2.0 m(高)。锚杆钢筋为HRB400级,锚固段注浆采用M20级水泥浆,半径40 mm。试验相关设计参数和传感器布置如图7、图8所示。

图6 框架锚杆支护边坡室外模型试验Fig.6 Outdoor model test of frame anchor support slope
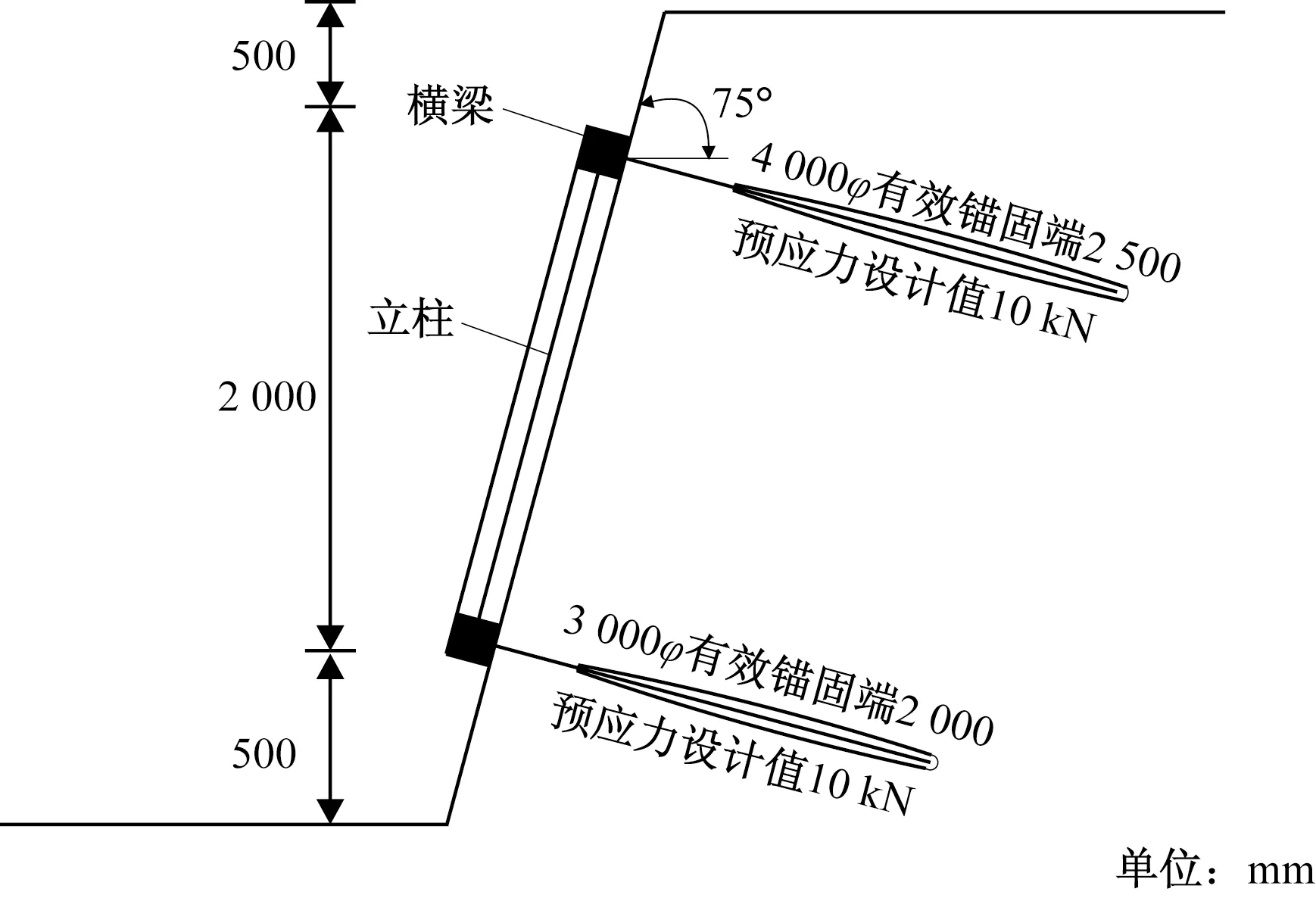
图7 模型示意图Fig.7 Model sketch map
3.2 参数取值
由地勘报告可知,试验场地土体为常见的高原地区黄土,土质均匀、松散、欠固结。通过室内试验得到地基土平均含水率为20.58%,内摩擦角为15°,黏聚力24.87 kPa,孔隙比为0.98。经判断,地基土属于弱冻土层,冻结温度Tf为-0.21 ℃。结合相关资料[16-18],基本特性参数如表1所示。

表1 基本参数Table 1 Basic parameters
冻土导热系数λf和融土导热系数λu分别表示为
(45)
冻土热容Cf和融土热容Cu分别为
(46)
导水系数kw为
(47)
未冻水与温度的关系可表示为
(48)
土体弹性模量E与泊松v分别表示为
(49)
(50)
3.3 计算模型
3.3.1 几何尺寸
结合试验模型和场地因素考虑,几何计算模型如图9所示。其坡高3.0 m,坡角为75°,长为6.8 m,宽为9 m。

图9 模型尺寸Fig.9 Model size
3.3.2 初始条件
对于温度边界条件,由于试验场地的日平均气温会低至为-4.1 ℃,结合室外试验实测结果,坡顶、坡面和坡脚的热边界条件为
(51)
式(51)中:t为时间,d。
土体初始温度由观测数据取夏季冻融周期外的平均温度4.5 ℃。
对于水分边界条件,由于正午温度的升高,地表水分蒸导致上边界水分散失,而降雨降雪导致上边界水分补充,左右边界及下边界无水分渗入或渗出,因此上边界的水分条件为
(52)
土体初始含水率由土样室内试验测定的20.58%。
位移边界条件:左右边界在x方向上固定y方向上自由,下边界x、y方向均为固定,其余边界自由。
3.4 试验结果验证
冻结深度随时间变化的曲线如图10所示。可以看出,前半段计算值与试验值较吻合,后半段与试验值相比偏大。从冻结深度曲线变化情况看,计算结果符合冻胀随时间发展的规律,因此本文建立的模型是宜用于季冻区边坡工程的设计和计算。
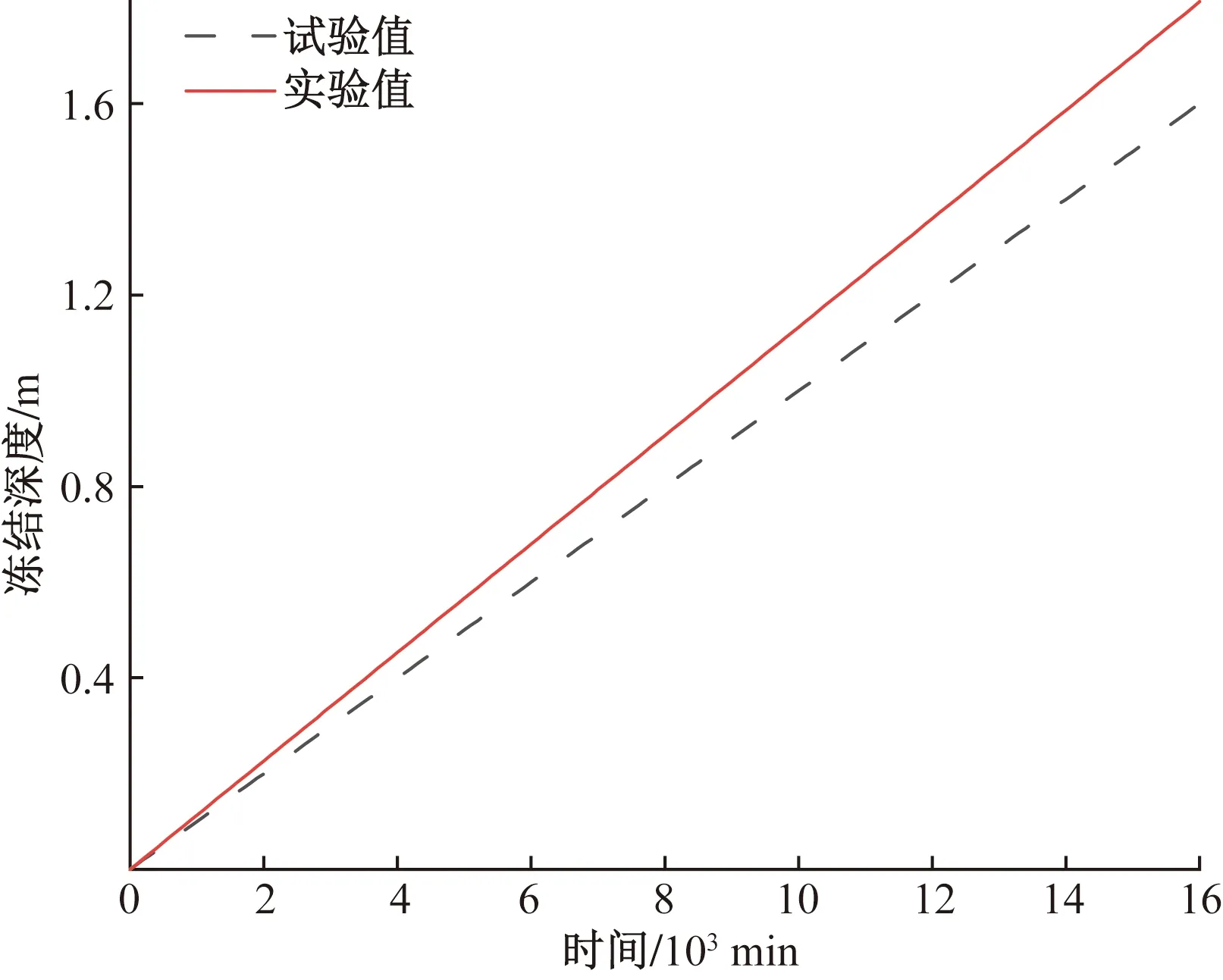
图10 不同时刻下冻结深度Fig.10 Frezzing depths at different time
4 结果与分析
由试验观测结果可知,最大冻结深度与最大融化深度分别出现在1月5日和4月4日。其中,冻结时表示冻深达到最大值,融化时表示融深达到最大值。
4.1 温度场
冻结时刻前后12 d的观测数据与计算值对比曲线如图11所示。冻结和融化时的温度云图如图12所示。
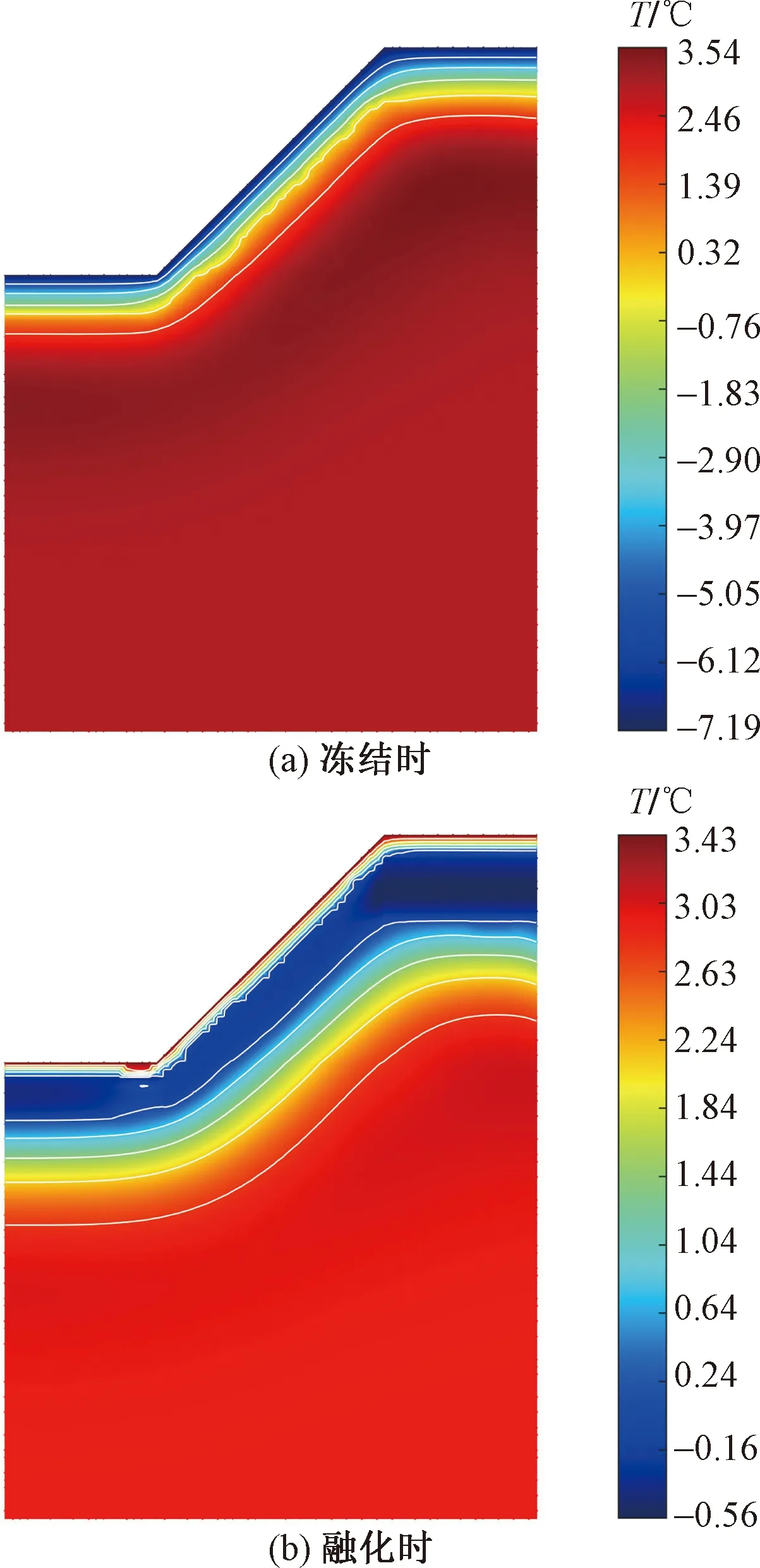
图12 温度云图Fig.12 Temperature nephogram
由图11可知,计算值整体比试验值小约2 ℃,但试验值和计算值呈现出相同的发展规律,随着时间的进行,温度逐渐降低,冻结深度不断往下发展。在最大冻深后,温度有小幅度的回升,可见,其变化符合冻胀规律,计算值与试验值基本吻合。
由温度云图(图12)可知,冻结最大影响深度约2.0 m,再往下温度基本保持稳定。受坡顶冻结的影响,坡面顶部冻深最大。融化时地表温度影响深度约1.5 m,受坡顶融化的影响,坡面融化深度沿坡面减小。结合冻结和融化的温度云图可知,在整个冻融过程中,坡体内部只有一定深度的土体温度发生了变化,这一部分土体经历冻胀和融化变形,其应力状态也随之变化,容易发生冻融滑塌,在实际工程中应重点观测该部分土体。
4.2 水分场
冻结时刻前后12 d的观测数据与计算值对比曲线如图13所示。冻结和融化时的水分云图如图14所示。
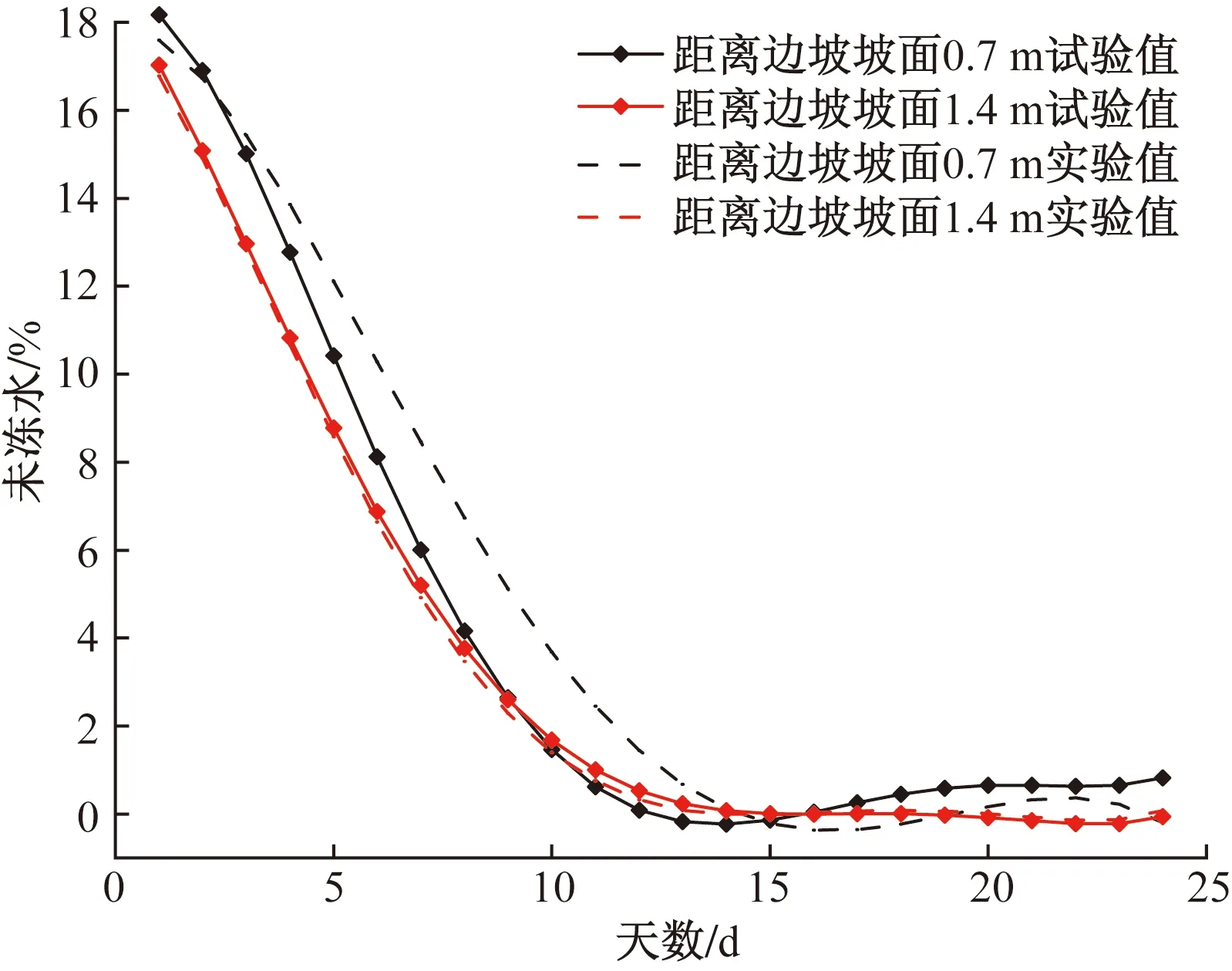
图13 未冻水对比Fig.13 Comparison of unfrozen moisture
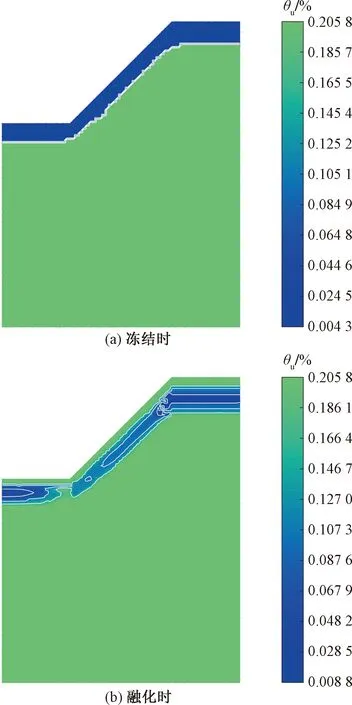
图14 未冻水云图Fig.14 Unfrozen moisture nephogarm
从图13可以看出,计算值比试验值要大约0.2%,但与试验值吻合相当好。随着冻胀变形的发展,未冻水含量不断减少直至水分完全冻结,这也符合实际情况。
未冻水含量与温度相关,由图14可知,冻结时未冻水云图与温度云图趋势接近。在2.0 m处分界明显。在融化土层内,受坡顶融化影响,坡顶未冻水量最低,沿坡面向下水分不断聚集。
4.3 应力场
冻结与融化时的剪应力云图如图15所示。冻结时土体性弹性模量的增加,导致了剪应力是融化时的2.5倍,冻结时剪应力沿坡面向下大致呈线性分布,在坡脚集中。在边坡其他区域剪应力分布均匀,因此在冻结时边坡整体是较稳定状态;融化时,剪应力在坡脚出现了明显的应力集中,在融化区域和未融化区域界面发生剪应力突变,边坡处于不稳定状态。
4.4 锚杆轴力分析
锚杆轴力如图16所示。在初始、冻结、融化3种工况下,结合试验结果与计算值对比分析可知,相比于初始时,由于在边坡坡面产生的冻胀变形,进而导致支护结构发生位移,直观的表现在第一排锚杆自由端轴力增加了约20 kN,第二排锚杆自由端轴力增加了约17 kN,并沿着锚杆长度方向变化量不断减小。离坡面越远,这种由冻胀变形引起结构的位移量越小,因此在锚固段轴力变化不大。3种工况下,冻结时锚杆轴力最大,融化后轴力大幅度降低,但仍然要比初始时的轴力值要大,而造成这种现象的原因是融化后土体应力发生了重分布,坡面产生了不可恢复的位移,从而导致锚杆无法恢复至初始工况下的轴力。
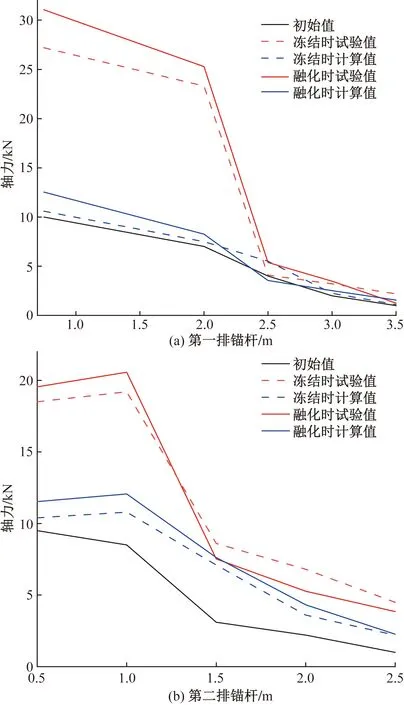
图16 锚杆轴力对比Fig.16 Comparison of Anchor Rod Axial Force
5 结论
(1)建立框架锚杆支护边坡的耦合计算模型,结合MATLAB编制了计算程序,并与室外试验对比分析,验证了程序的可靠性。
(2)在试验过程中存在只有一定深度的土体仅受到冻融影响,这一深度可以通过计算得到。与冻结时相比,融化时锚杆轴力大幅度降低,但仍留有残余应力,表明冻融作用对结构内力影响较大,在采用结构支护边坡时,应按冻胀工况对结构进行设计。
(3)考虑多物理场耦合作用,通过试验和理论计算,对框锚支护边坡在单次冻融条件下各物理场反映的规律进行分析,但并没有进一步分析多次冻融循环条件下各物理场的变化,需在以后的工作中对此部分进行深入研究。
