基于改进DPSO非退出故障下多无人机任务规划

邵士凯, 李厚振, 赵渊洁

(河北科技大学电气工程学院, 石家庄 050018)

随着技术的进步,无人机在各个行业均得到广泛的应用。在复杂的战场上,多机协同执行任务是无人机技术的研究热门,尤其是多无人机协同执行打击任务是无人机智能化、多样化的重要组成部分[1-3]。

当前发展成果中,无人机任务分配的主要控制方式包括集中式、分布式与分层次控制。文献[4]针对地面目标的动态任务分配问题,建立了两种分配模型,并与基于合同网算法、智能优化算法、聚类算法等进行对比,分析了其优缺点及研究现状。文献[5]提出了一种离散狼群算法的任务分配方式,对高维复杂问题进行功能性优化,并通过正交实验和方差分析,证明离散狼群算法(discrete wolf swarm algorithm, DWSA)具有较好的收敛性。文献[6]提出了一种将3种激光扫描数据与无人机航空影像融合的拱桥精细化建模方法,并通过实景三维模型为类似底部脱空建筑的数据采集方法提供了参考。文献[7]提出了一种差分进化-离散粒子群优化-郭涛-模拟退火(differential evolution-discrete particle swarm optimization-Guo Tao-simulated annealing,DE-DPSO-GT-SA)算法的协同多任务分配,并进行了多种算法的对比,仿真实验证明该方法具有较好的收敛特性。文献[8-9]考虑实际环境下无人机任务分配的协同能力,加入了复杂的地形约束。文献[10]提出了一个由嵌入式硬件和高级别通信协议相结合的系统,作为识别、分发和分配任务的基础,进而用简单分散的方式供多无人机使用。文献[11]提出了一种动态离散鸽群的优化算法,进行处理多无人机协同搜索攻击任务规划,集成了任务分配和路径生成。综上可知,关于目前多机协同任务分配的研究,仅考虑了算法的改进和一对一的目标分配,而针对无人机发生故障后的多对一任务分配问题考虑不充分。

此外,当任务分配完成后,为保证无人机到达任务目标点,还需要进行无人机轨迹的设计与规划。当前无人机航迹规划的研究中,大部分成果仅针对单架无人机的航迹进行了深入的探索,多机的航迹规划以及与任务分配的耦合程度尚未进行有效研究。运用图论的方法进行一些路径规划是当前研究的一种思路,如A*算法[12]、匈牙利算法[13]、随机树算法[14]、Voronoi图形算法[15]等。这类方法由于均是基于代价图进行规划的,需要进行离线存储好代价图,从而导致该方法较费时。随着人工智能技术的发展,仿生物群体捕食技术的算法被广泛应用于航线规划中,应用较广泛的算法如蜂群算法(bee colony algorithm,BCA)[16]、狼群算法(wolf swarm algorithm,WSA)[17]、遗传算法(genetic algorithm,GA)[18]以及粒子群算法(particle swarm optimization,PSO)[19]等。其中粒子群算法因搜索能力强、易仿真操作等优势被广泛应用,文献[20]提出了将粒子群算法进行航线预规划,并结合高斯伪谱法进行拟合进行航线规划的方法,该方法有效提高了收敛速度,航线平滑性更好。文献[21]考虑无人机航迹在三维空间结构的特点,提出了一种遗传算法和模拟退火算法相结合的算法,通过三维有限空间仿真验证了该算法可实现最优航迹的有效缩短,同时迭代次数也得到了相应的减少。

综上所述,针对多无人机打击任务规划,当前研究大都只考虑了一对一的打击规划场景,即一个敌方目标只由一架无人机进行打击,且仅考虑了任务分配的直线距离,不符合实际作战环境下的航迹规划,从而造成规划结果不避障;同时,当前无人机任务规划研究中仅涉及任务分配或者航迹规划的一方面内容,没有考虑现实状况下二者耦合情况;另一方面,当无人机发生故障后,各机协同执行任务的有效性尚未进行有效探究。

基于此,针对无人机发生故障下多对一的协同打击任务规划进行了研究,将任务分配与航迹规划进行耦合。首先,针对障碍环境下的多无人机-多目标分配场景,进行任务分配算法建模,分配过程中考虑了雷达障碍等因素,同时算法不基于无人机-目标的直线距离,而是耦合基于航线规划的实际飞行距离;其次,提出一种基于混合改进策略的离散粒子群任务分配算法,利用Sobol序列进行种群初始化,基于柯西算子、非线性时变变异策略,以及自适应交叉学习策略更新优质个体,丰富种群的多样性;最后,在山峰、雷达等威胁约束下,进行无人机故障前后仿真实验。为部分无人机发生轻微故障后,多机协同执行任务规划的问题提供了理论依据。

1 问题描述

假设无人机群在执行打击任务的过程中,部分无人机发生轻微故障,在不退出战斗序列的情况下,飞行能力受限,只能对局部范围内的目标进行打击,剩余无人机调整状态,协助故障机重新完成对新目标的打击任务。因此,为使任务规划结果最优,需在合理的约束条件下将无人机按照最低损耗成本进行任务分配。

定义存在m架无人机,te个敌方目标,且m>te,执行多对一的打击任务,即无人机对不同标号的目标进行不同架次的打击。当有无人机发生故障时,重新协调各机机动性能和飞行成本,在满足各种约束的情况下,完成任务分配。

在任务分配完成后,各机根据给定的航迹点运用三次样条插值的方法执行航迹规划,最终准确打击目标。

1.1 约束条件

1.1.1 打击次数约束

假设无人机执行任务分配时,对目标i执行打击的次数表示为MAttack(i),目标点数集合表示为t,则打击次数可表示为

(1)

式(1)中:当目标标号t为偶数时,无人机进行A1架次的打击;当目标标号t为奇数时,进行A2架次的打击,具体打击次数根据仿真进行设定。

该约束的优化约束指标函数为

(2)

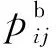
1.1.2 空间协同约束

对于多无人机协同飞行时,考虑无人机之间因发生碰撞导致任务失败的情况,建立具有空间协同能力的约束条件,设定任意两架无人机之间的距离为d,为避免碰撞,d应满足:

d>dmin

(3)

式(3)中:dmin为机间最小安全距离。

其对应的优化约束指标函数为

(4)

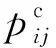
1.1.3 总航程最短约束

当前无人机任务分配的研究中,航程约束仅基于直线距离的规划,不符合无人机实际飞行轨迹,即基于直线距离的任务分配不一定满足存在障碍飞行环境下的最优分配结果。故提出的总航程最短约束将无人机实际飞行航程作为约束条件考虑在内。

假设S1表示无人机从起始点到敌方目标点需要付出的航程代价,为更加直观地表现目标函数的适应值变化,对航程代价约束值进行归一化处理,具体表示为

(5)

li=sqrt[(xk+1-xk)2+(yk+1-yk)2+

(zk+1-zk)2]

(6)

式中:η为航迹点总数;k为某一航线点;xk、yk、yk+1、xk+1为该航线点在水平面上的坐标;zk、zk+1为航线点的垂直高度;lstr为无人机任务分配完毕后起点与目标点的直线距离。

航线规划的结果即是在任务空间中,通过搜索一系列的航迹点,经过迭代寻优得到符合最短总航程约束的点,从而构成可飞行航迹。

此外,考虑到无人机在实际作战环境中,存在山峰和雷达监测的威胁,当无人机进行航迹规划时,需要将其考虑在内,故引入如下约束条件。

1.1.4 雷达威胁约束

多无人机在执行任务飞行时需避免被敌方目标设置的雷达监测到,假设雷达探测范围表示为半球形,且不会被周边地形遮盖,则多无人机在执行任务的航线规划过程中,其雷达威胁模型设置为

Lradar=(xk,yk,zk,rk)

(7)

式(7)中:xk、yk、zk为雷达所在的中心位置;rk为其监测半径。

(8)

其优化约束的指标函数为

(9)

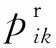
1.1.5 山峰威胁约束

在实际环境中,多无人机协同执行任务分配时,还需要规避飞行区域内的山峰。因此,机群应与山体威胁保持一定航距。则山峰威胁约束的建模形式为

(10)

式(10)中:xu、yu、zu为山峰威胁的三维坐标位置;a、b为山峰的起始位置;c为山峰的高度;d为可调节系数;k′为山峰的面积跨度。

其优化约束的指标函数为

(11)

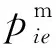
1.2 评价指标

多机协同任务规划需满足上述各约束条件,使各机任务规划优化性能达到最优。因此,目标函数表示为

S=c1S1+c2f2+c3f3+c4fR+c5fM

(12)

式(12)中:S为总代价值;S1为总航程最短约束代价;f2为打击次数协同约束惩罚值;f3为空间协同约束惩罚值;fR为雷达威胁惩罚值;fM为山峰威胁惩罚值;c1、c2、c3、c4、c5为各约束指标所占权重值,满足:

c1+c2+c3+c4+c5=1

(13)

2 求解策略

2.1 改进离散粒子群算法

由于传统离散粒子群算法求解效率慢,适用性差,提出了一种混合策略改进的离散粒子群算法(mixed strategy improved discrete particle swarm optimization,MSDPSO),有效提升了算法的寻优结果和收敛速度,具体改进如下所示。

2.1.1 基于Sobol序列初始化策略

由于离散粒子群算法(discrete particle swarm optimization, DPSO)采用生成[0,1]之间生成伪随机数的方式进行种群初始化,组织性和遍历性差,且个体分布不均匀,从而导致寻优性偏低。采用Sobol序列进行初始化,使得种群分布更为规范、解空间覆盖率更高,进而提升算法的寻优精度。图1为伪随机分布与Sobol序列分布初始化的对比。

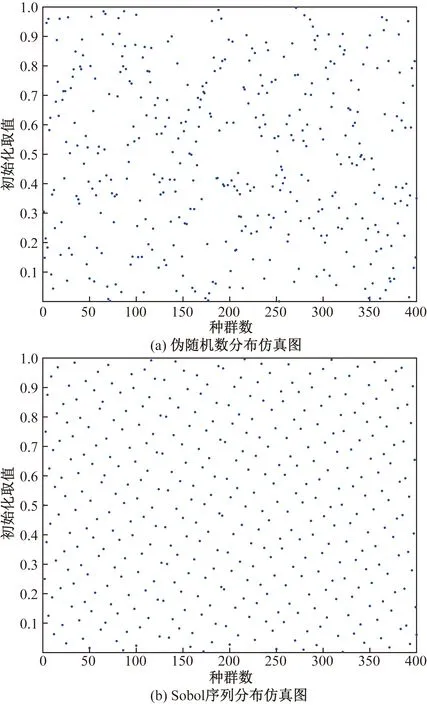
图1 种群初始化方法对比Fig.1 Comparison of population initialization methods

由图1对比可知,采用Sobol序列进行种群初始化后的解空间覆盖率比传统初始化方法更高,且分布更规范。从而提高算法收敛速度。

2.1.2 非线性时变策略

DPSO借鉴遗传算法的思想,离散化PSO的粒子位置和速度,更新为交叉和变异策略,其变异策略不能及时根据位置的变化做出相应的调整,从而导致寻优性变差,为解决该问题,引入非线性时变策略:

(14)

如式(14)所示,将变异策略分为3个阶段,其中,T为最大迭代次数,t′为当前阶段的迭代次数,在变异策略处于算法的后期阶段,此时解的寻优性较差,故设计非线性时变的变异因子的前两个阶段能够加强粒子的变异能力,从而及时摆脱局部搜索,提高解的寻优能力,随着迭代的进行,适应值趋于最优,变异因子随之进入第三阶段的线性环节,从而加快算法的收敛速度。a′、b′分别为不同阶段的系数因子,具体数值根据仿真进行设定。此外,交叉因子r1、r2也会影响粒子的更新速度与寻优能力,为进一步提高算法的收敛速度与全局寻优能力,对交叉因子进行线性改进,可表示为

(15)

(16)

交叉因子r1随着迭代的进行而增加,r2随迭代次数的累加而减小。

这使得算法在迭代开始阶段积极进行全局搜索,进而提升收敛速度,随着迭代接近尾声,个体学习能力的加强使得种群不易陷入局部最优,同时,r1与r2的和为1,表示粒子兼顾寻优能力和收敛速度。

2.1.3 柯西变异策略

针对DPSO易陷入局部最优的特点,引入柯西算子能够有效提升算法的全局搜索能力,增强搜索空间。由于柯西分布函数在中点的步长较小,在两端的步长较大,从而对粒子个体产生较大扰动,使得粒子能够及时调整位置,避免陷入局部最优。同时,柯西分布峰值下降的坡率较缓且峰值较小,从而使得粒子经过变异后用于搜索的时间花费较少,进而能够把更多的时间用于全局寻优上,因此提高了改进算法的收敛速度。

经过离散化的算法采用如下改进的柯西变异公式,进行更新当前个体的最优位置,提高全局寻优能力。

(17)

从而增强全局寻优能力,提高了改进算法的收敛速度。

2.1.4 自适应交叉学习策略

针对传统离散粒子群算法全局寻优能力差的特点,在迭代前期及后期加入自适应交叉学习策略,将粒子之间的交叉置换拟化为人与人之间交流学习的方式,通过交流比较,粒子不断进行个体寻优从而改善自身状态,可表示为

(18)

式(18)中:Xnew为通过加入自适应交叉学习策略,将粒子之间的交叉置换拟化为人与人之间交流学习的方式,通过交流比较,粒子更新得到的新个体;f(x)为通过离散粒子群算法不断迭代得到的任务序列;x为随机粒子;xp为相邻粒子;rand为产生(0,1)之间的随机数,用于放大个体之间学习的过程,通过不断迭代,更新个体最优,从而丰富了种群的多样性,进而提升改进算法的全局寻优能力。

2.2 无人机航迹规划

2.2.1 粒子群算法

为保证任务分配的合理性,需要为无人机到达目标点制定合理避障的飞行路线。故基于基本粒子群算法进行航线预规划。其数学模型为

(19)

(20)

2.2.2 三次样条插值算法

与基于直线距离的任务分配相比,航线预规划能够保证更好的任务合理性,然而预规划得到的航线是一系列相对粗糙的航迹点,导致无人机轨迹不平滑。因此,运用三次样条插值算法,对PSO的预规划航线进行再优化,从而得到更加平滑的无人机航线。

假设a=η0<η1<…<ηn=b,其中,ηi为航迹点,i=1,2,…,n,在区间[ηi-1,ηi]上的分段函数s(η)为小于或等于三次的多项式且二阶可导。可表示为

s(η)={si(η),η∈[ηi-1,ηi],i=1,2,…,n}

(21)

si(η)=aiη3+biη2+ciη+diη3

(22)

式(22)中:ai、bi、ci、di为待定系数,其和为4n。

一般情况下,为得到三次样条插值函数s(x)的待定系数ai、bi、ci、di,采用自然边界条件,即

s″i(xi)=s″i(xn)=0

(23)

综上,结合式(21)～式(23)进行联立方程组来确定待定系数值。

2.3 流程设计

根据上述方法的介绍,基于混合策略改进的离散粒子群算法进行故障下多无人机任务规划的流程步骤如下。

步骤1设定基本参数。给定无人机、目标点位置,设定环境障碍参数,包括雷达威胁的个数及监测中心坐标与半径,山峰威胁的个数及相关参数。

步骤2初始化种群数量,设置粒子个体极值和全局极值的初值,以及最大迭代次数。

步骤3开始进行迭代寻优,编译适应值函数并输入多约束条件,给定相应惩罚值,计算每次的代价值,并画出代价值函数曲线。

步骤4根据每次迭代的代价值,判断粒子当前迭代值与个体极值的大小情况,如若连续10次迭代值相等,执行柯西变异策略,帮助跳出局部最优;否则不执行此策略,直接进入下一步骤。

步骤5执行改进离散粒子群算法的交叉策略,并依据改进算法依次执行公式(14)的的非线性时变策略,并将当前迭代次数与最大迭代次数进行比较,直至执行完设定的最大迭代次数。

步骤6依据任务分配得到的分配结果,利用粒子群算法进行航线预规划。

步骤7根据粒子群算法航线预规划的结果,运用三次样条插值算法对航迹进行再优化。

具体仿真流程设计如图2所示。

图2 故障下无人机任务规划算法流程图Fig.2 Flow chart of UAV task planning algorithm under fault

3 仿真与分析

3.1 仿真参数设定

根据流程设计,在配置为Intel 5,1.19 GHz的计算机上,运用MATLAB2020b进行仿真实验。设定迭代次数T=200,种群数N=400;航迹点η=10;打击次数A1=3,A2=2;无人机安全间距d=20 m。

设定三维地形环境为250 km×250 km×70 km的任务区域,包括5个雷达监测区域和2个山峰威胁区域,雷达区域在仿真环境中以半球进行绘制,山峰则用高低起伏不同的曲面进行绘制。其参数设置如表1所示。

表1 威胁参数Table 1 Threat parameters

将无人机拟化为质点,并忽略相关的动力学模型。假设初始状态下,无人机未发生故障时,以12架无人机打击5个敌方目标为背景进行仿真实验,坐标位置如表2所示,目标点位置如表3所示。各无人机从起点出发,满足各约束条件下打击所有目标点。

表2 无人机起点位置参数Table 2 UVA starting point position parameters

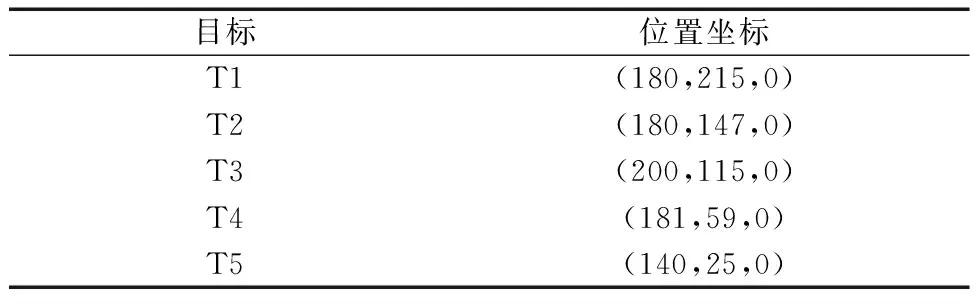
表3 目标点参数Table 3 Parameters of target point area

3.2 仿真结果分析

3.2.1 改进算法性能对比

根据不同策略方法,分别对传统的离散粒子群算法进行改进优化,得到以下4种单策略改进的离散粒子群算法:基于Sobol序列初始化改进的离散粒子群算法(sobol discrete particle swarm optimization,SDPSO);基于非线性时变的变异因子改进的离散粒子群算法(nonlinear time-varying discrete particle swarm optimization, NDPSO);基于柯西变异策略改进的离散粒子群算法(Cauchy discrete particle swarm optimization, CDPSO);基于自适应交叉学习策略改进的离散粒子群算法(re-cover discrete particle swarm optimization, RDPSO)。将以上4种改进算法与传统的离散粒子群算法(discrete particle swarm optimization, DPSO)以及MSDPSO进行仿真对比。

为了验证改进算法的有效性,分别将MSDPSO与SDPSO、NDPSO、CDPSO、RDPSO和DPSO进行了对比仿真,并同时进行了10次、30次、50次以及100次蒙特卡罗仿真,求其平均值后得到图3所示算法适应值对比结果。

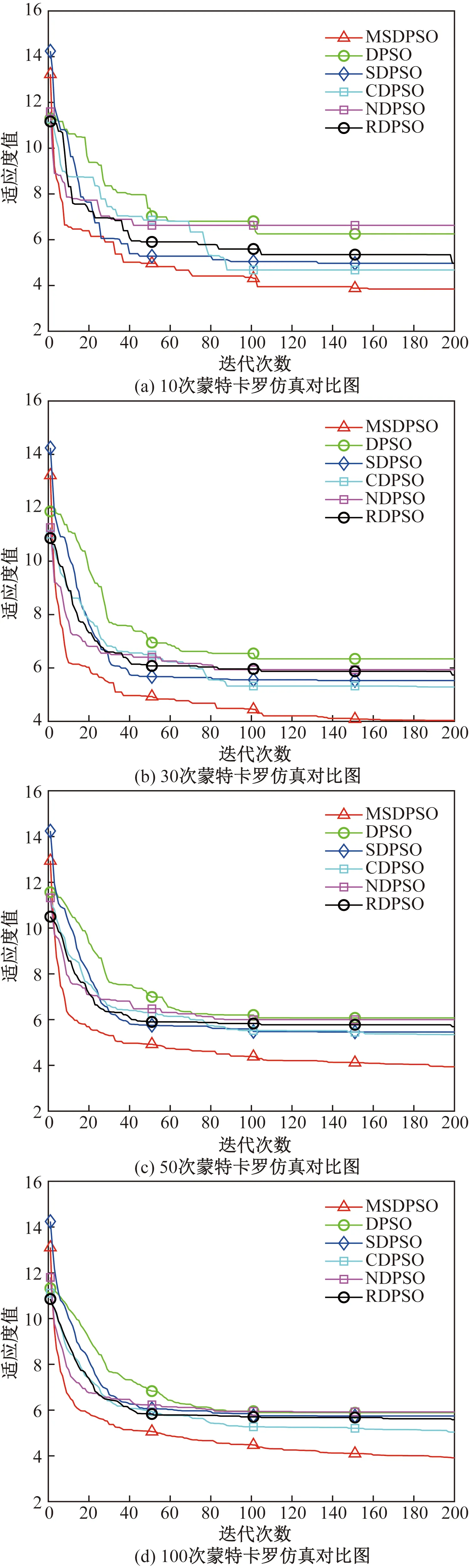
图3 改进算法适应值比较Fig.3 Comparison of fitness values of improved algorithms

根据图3仿真对比结果,经过多次蒙特卡罗仿真,MSDPSO在历次迭代寻优性能上均优于DPSO和其他单策略改进算法,寻优有效性较好。

此外,为验证MSDPSO的寻优稳定性和有效性均优于DPSO,分别给出100次仿真下的具体适应度曲线。仿真结果如图4所示。

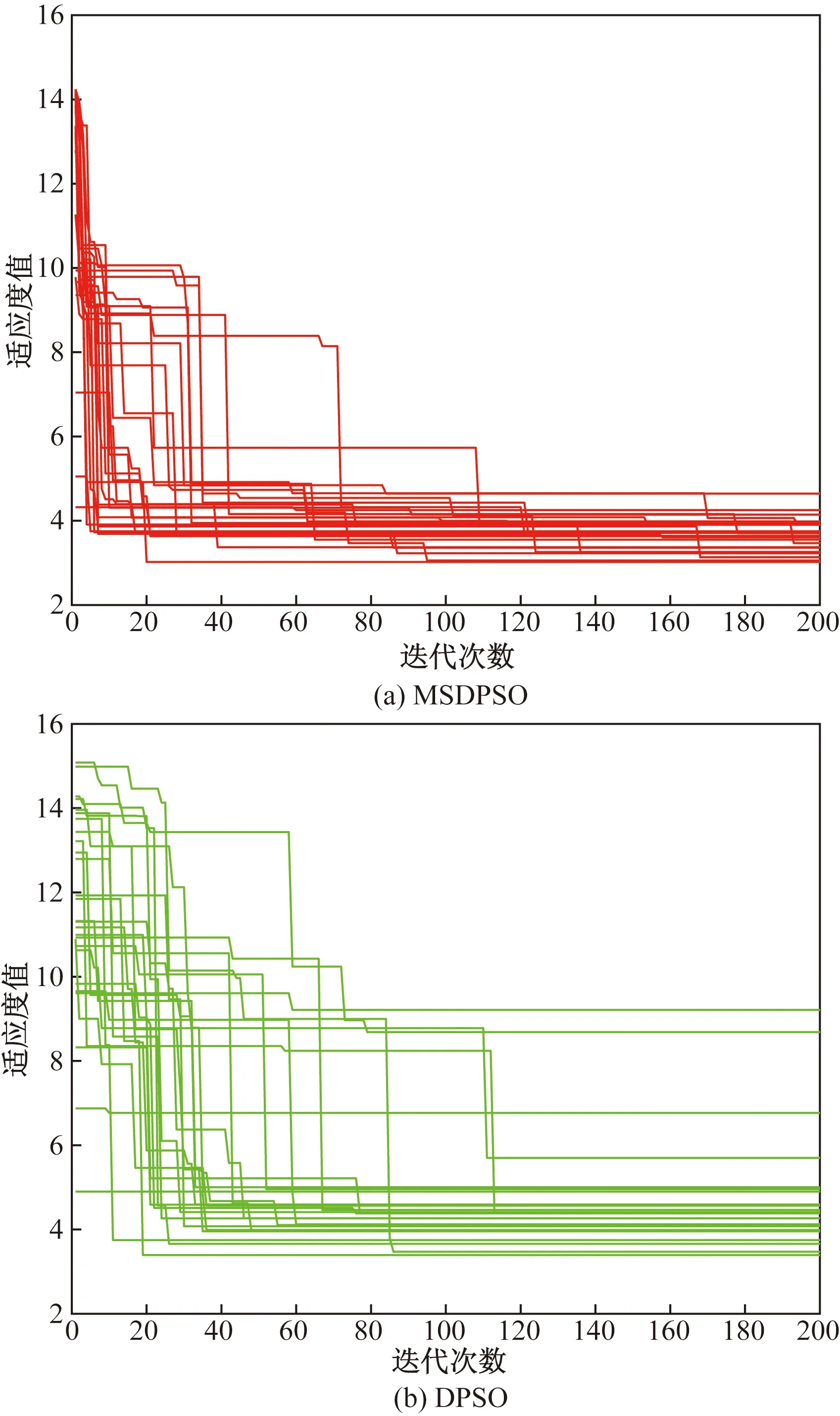
图4 适应值变化曲线Fig.4 Fitness curve

从图4可以看出,基于MSDPSO的适应值变化曲线较基于DPSO的适应值变化曲线更加稳定且有更好的收敛性,说明MSDPSO具有更稳定的寻优性,且最优值比DPSO更好,验证了MSDPSO具有更高的全局寻优能力,收敛速度也更快。

3.2.2 基于三次样条插值航线再优化

由于基于PSO的航迹规划,航线粗糙且平滑度低,利用三次样条插值的方法进行航迹再优化,可以使航线更平滑,且与MSDPSO的耦合程度更高。故基于三次样条插值的航迹再优化与基于PSO的航迹预规划进行了仿真对比,如图5、图6所示。

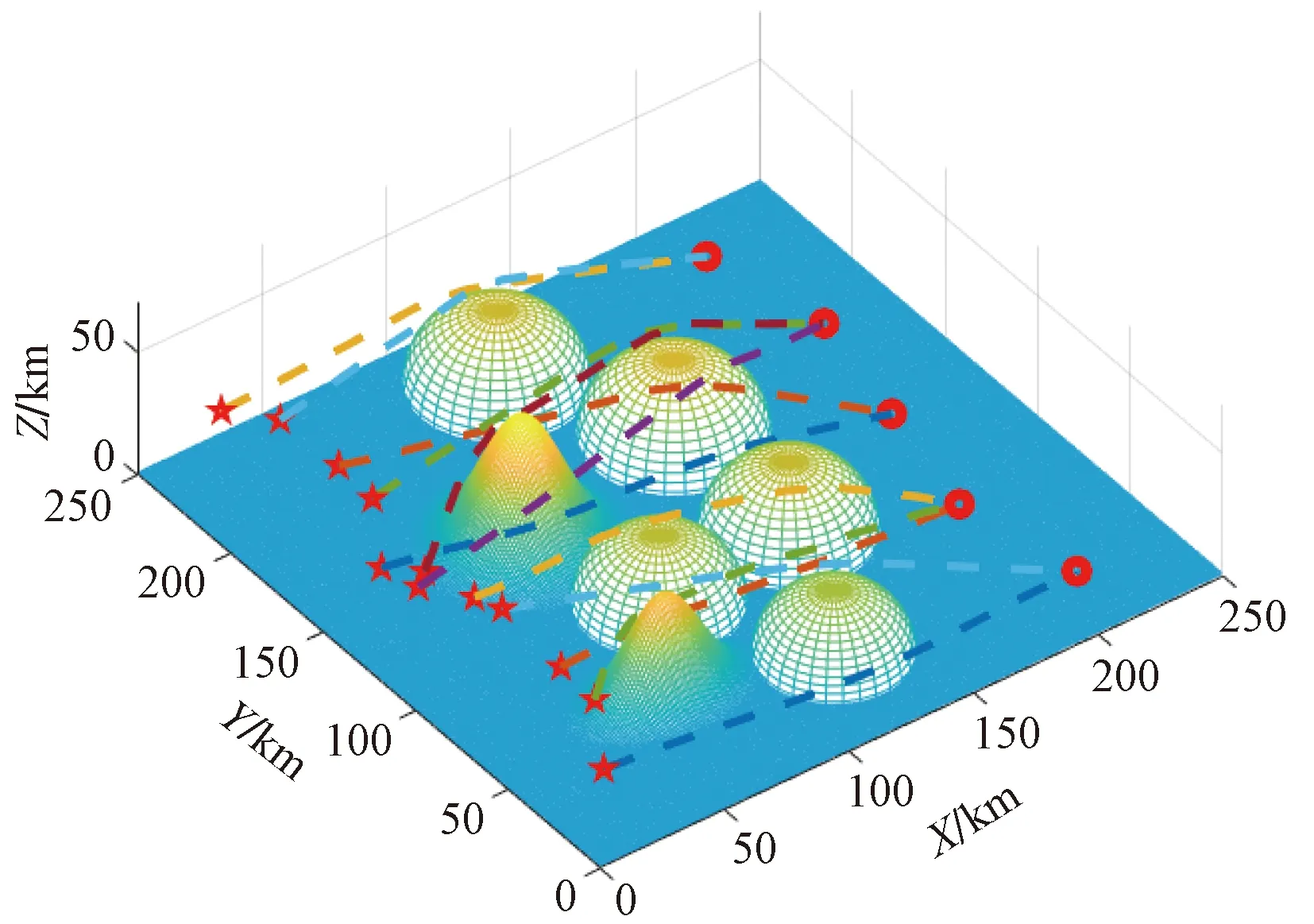
红星表示无人机的起始点;不同颜色的虚线是每架无人机基于PSO得到不同的轨迹规划,通过颜色对比可以更加直观地看出各无人机满足各项约束条件,有效躲避障碍物

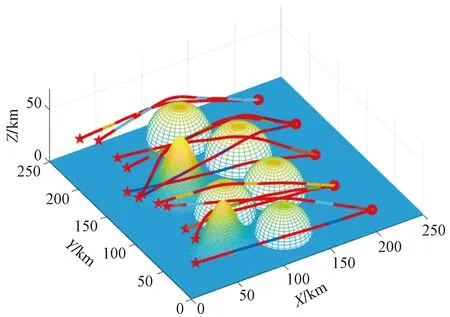
红星表示无人机的起始点;不同颜色的实线是基于PSO得到的航线是离散的轨迹点,在此基础上,利用三次样条插值的方法对轨迹进行再优化,可以得到更加平滑且连续的无人机轨迹,进而证实运用三次样条插值算法进行无人机航线再优化更符合无人机实际飞行

通过前后的仿真对比可以看出,基于PSO得到的航线是离散的轨迹点;经过三次样条插值优化过的无人机轨迹更加平滑且连续,证明运用三次样条插值算法进行无人机航线再优化更符合无人机实际飞行。

3.2.3 正常状态下多无人机任务规划

为与故障后的任务规划结果进行对比,首先基于MSDPSO进行正常状态下的多无人机协同任务分配,然后利用三次样条插值算法进行无人机的航迹优化,在各约束条件下并结合相关参数进行了如图7所示的仿真实验。

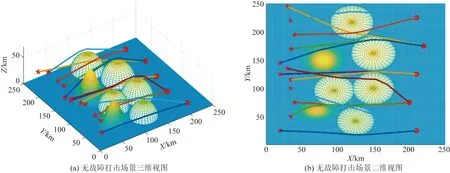
红星表示无人机的起始点;不同颜色的实线是为验证基于MSDPSO在无人机群无故障场景下的有效性,通过仿真实验得到每架无人机不同的打击任务规划,同时与图8、图9的故障场景进行对比实验

根据仿真结果可知,基于MSDPSO各无人机在正常状态下均优化得到最优打击任务分配,实现了无人机多对一的打击场景,且结合多无人机航迹规划,成功实现了对障碍物的避障,证明了改进算法具有良好的应用有效性。

3.2.4 故障后多无人机任务规划

假定该12架无人机在执行打击任务过程中,第2、8号无人机在原航迹规划的第3个航迹点发生机动故障,丧失部分打击能力,无法按照原定任务进行打击,需要整合各无人机重新进行任务规划。如图8所示。

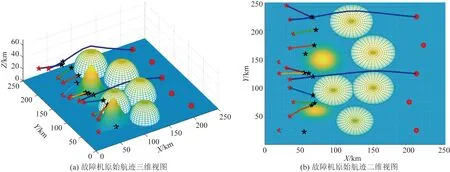
红星表示无人机的起始点;黑星表示无人机发生故障时的航迹点位置;不同颜色的实线表示的含义是第2、8号无人机发生故障前,各无人机原始的任务规划

根据图8仿真信息可知,故障前,第2号、8号无人机分对1号、3号目标进行打击;且故障前已对无人机打击次数进行了约束,此时第2、8号无人机发生故障而仍保存部分行动能力,剩余无人机的状态并未受到影响。因此,通过减小对故障机的最短航程约束,允许故障机在能力范围内对就近目标优先进行打击,其他约束条件保持不变,基于MSDPSO对各无人机进行任务重规划,继续完成打击任务。具体仿真结果如图9所示。

表示有无人机发生故障后,剩余的健康无人机基于MSDPSO得到的任务规划结果;表示第2、8号无人机故障前后的任务规划结果;红星表示无人机的起始点;黑星表示无人机发生故障时的航迹点位置

为与故障前无人机的任务分配形成对比,图9在图8的数据基础上进行的仿真实验,保留了第2、8号无人机故障前的航线信息,即蓝实线所表示的航线。通过黑蓝实线的对比,并结合仿真图10所示的故障前后MSDPSO打击任务分配结果可以看出,故障前,第2号、8号无人机分别对1号、3号目标点进行打击;故障后,第2号无人机依然针对1号无人机执行打击任务,说明2号机在故障受损的控制范围内,基于MSDPSO可以搜索到距离自身故障位置最近的1号目标进行打击,验证了MSDPSO具有有效的寻优能力,而8号机转换为对4号目标点进行打击,说明无人机协同执行任务规划过程中,健康无人机可以根据态势变化,迁就故障机根据其故障状态优先选择目标点进行打击。

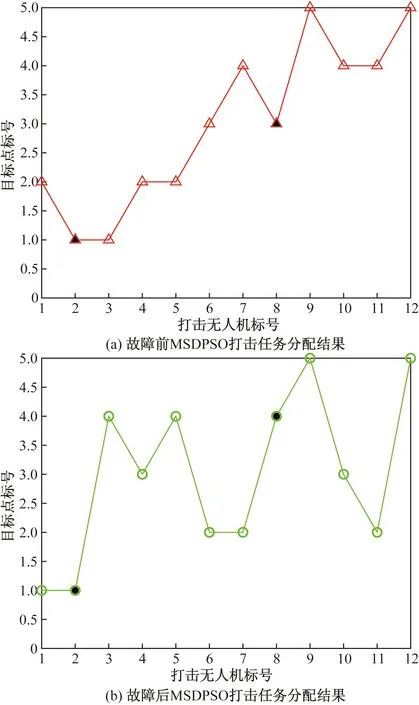
黑色三角、黑色圆点分别表示无人机2、8号在故障前后的打击任务分配结果

根据图11无人机间距仿真信息,各无人机在执行任务过程中,机间距离均大于设定的最小值,满足空间协同约束。

4 结论

针对非退出故障下多无人机执行多目标任务规划的问题,提出了一种混合改进策略的离散粒子群算法进行求解。利用Sobol序列进行种群初始化,基于柯西算子、非线性时变的变异策略,以及引入自适应交叉学习策略,提高了算法寻优能力和收敛速度。为得到公正且信服的评估,将各无人机在多种约束条件下进行了多组蒙特卡罗模拟仿真,并与传统离散粒子群算法和单策略改进下的算法进行了充分比较,验证了所提出的MSDPSO的有效性。得出如下主要结论。

(1)MSDPSO比DPSO、SDPSO、NDPSO、CDPSO和RDPSO获得更好的最优解。

(2)MSDPSO的收敛速度比各DPSO更快。

(3)混合策略改进下的DPSO可以优化得到更佳的分配方案,从而降低任务规划成本,验证了所提方法的有效性。