格宾网片拉伸试验的有限元法数值实现

2023-12-14李立云吴浩瀚李雷

科学技术与工程 2023年32期

李立云, 吴浩瀚, 李雷

(北京工业大学城市建设学部, 北京 100124)

格宾网片是镀锌低碳钢丝织成的金属网,广泛应用于土木水利工程领域内,如防护岩崩落石[1]、边坡防护[2]、路堤稳定性增强[3]和堤岸防护[4]中。目前,格宾网片的力学性能研究多采用物理试验展开,以获得材料特性或校准数值模型[5-6]。基于物理试验,人们明晰了格宾网片宏观力学性能和变形破坏特征,发现影响网片拉伸强度的关键因素有网孔尺寸、网丝直径和绞边方式[7-8]。然而,通过物理试验所获的力学指标有限,若进行更细致研究则需布设大量传感器,导致物理试验实施存在诸多困难和不确定性。数值模拟方法可以消除物理试验中的施作困难和不确定性,为研究网片各组分对其整体力学性能的影响带来便利性,进而优化网片设计或改进物理试验方案[9]。

网片力学性能数值研究中最常采用的为离散元法[10-12]。但是,格宾网片的离散元模型过度依赖物理试验进行校准且不能反映网片的三维变形特征。众所周知,有限元法适用于具有非线性几何形状、复杂力学行为和各种接触条件的连续介质问题,为降低计算成本,一些使用桁架单元或膜单元的简化网片有限元模型被提出[13-14]。但是,简化网片模型不能准确描述荷载作用下网丝的力学响应,实际风险点位可能被忽略。现存少数可用的三维数值模型虽已较为成熟,但都十分复杂。因此,构建一个正确可信、方便快捷的三维格宾网片有限元模型,是对网片开展更深入力学性能研究中亟待解决的问题,还具有推广格宾结构实际工程应用的价值。

鉴于此,聚焦于格宾网片拉伸试验的数值实现,探讨格宾网片精细化三维模型[15]在有限元数值模拟中的适用性和择取关键参数的可靠性,首先基于三维精细化建模方法建立格宾网片数值模型,并将其移植于有限元软件Abaqus中模拟恒定速率下的准静态拉伸试验。之后,分析网片系统的能量曲线,探讨保证模拟结果可靠的情况下控制计算成本的最优方案。最后,通过对比分析数值模拟与物理试验结果,验证模拟方法的合理性及模拟结果的正确性,揭示拉伸荷载作用下格宾网片的变形特征以及应力分布情况。为进行不同规格网片的拉伸试验创造有利条件,为后续格宾结构力学性能的深入研究奠定基础。

1 网片特征及夹持方式

格宾网片的几何特征按空间结构分为六边形网孔、边丝和端丝,如图1(a)所示。几何尺寸为长幅L、宽幅W、网丝直径d和网孔尺寸M×N,网孔尺寸由双绞合网丝轴线之间的距离M与上下两结点之间的距离N控制,如图1(b)所示。

s为双绞丝长度

以尺寸L×W=1 000 mm×1 000 mm的网片物理拉伸试验[15]为基准。物理试验中网片被夹具夹持的尺寸范围为930 mm×660 mm,夹持方式如图2所示,根据《工程用机编钢丝网及组合体》(YB/T 4221—2016)夹持[16]。

黑色圆点表示夹具和网片之间的连接点

2 格宾网片数值模型

2.1 格宾网片三维有限元建模

格宾网片的数值模型采用笔者提出的三维有限元精细化建模方法[15]实现。该方法基于SolidWorks软件和ABAQUS软件的结合,充分考虑了网片的空间复杂性,通过捕捉网丝的运动轨迹实现复杂网片建模。网片建模过程如图3所示。

图3 格宾网片建模流程图Fig.3 The modelling procedure of gabion mesh

格宾网片模型通过复制装配相互交织缠绕且做圆柱螺旋运动的单根网丝得到,构建单根网丝模型所需的参数为:双绞丝长度s=30 mm、网丝直径d=2.5 mm、网孔尺寸M×N=80 mm×100 mm以及双绞丝缠绕数n=3次。根据上述参数,利用SolidWorks软件建立单根网丝模型,并在Abaqus中完成装配,得到格宾网片数值模型如图4所示。

网丝间接触定义为通用接触,切向摩擦系数0.3,法向硬接触以严格控制模型穿透。为模拟物理试验中夹具作用于网片的拉伸荷载,对数值模型边界条件做如下处理:首先,设定图4中标识为RP的参考点,耦合上部端丝到参考点RP-1,并使该点1 000 s内沿y轴正方向拉伸170 mm,加载方式采用平滑分析步以减少初始荷载施加时对网片造成的影响;耦合下部端丝到参考点RP-2,该点完全固定。其次,约束黑色圆圈内双绞丝x方向的位移。

2.2 网丝材料参数标定

低碳钢丝是典型具有长塑性阶段的材料,为在数值模拟中准确地描述其变形过程,定义材料属性时要对在物理试验中得到的本构模型数据进行标定。参考朱凯[17]的2.7 mm网丝物理拉伸试验结果,如图5所示。

图5 网丝的应力-应变曲线Fig.5 Stress-strain curves of the wire

数值模拟中的材料属性参数包括网丝弹性模量E、真实应力σt和塑性应变εp。根据图5初始直线段,可以计算得出弹性模量E=20 GPa。但是物理试验得到的应力-应变数据为名义应力σn和名义应变εn,由式(1)、式(2)获得。数值计算中所需的真实应力σt和塑性应变εp需要通过名义应变εn和名义应力σn转换获得:由式(3)、式(4)计算得出真实应变εt和真实应力σt,并由式(5)得到塑性应变εp。

(1)

(2)

式中:Δl为网片钢丝长度的变化量;l0为网片钢丝的初始长度;F为荷载;A0为网片钢丝的初始截面面积。

(3)

(4)

式中:l为网丝的当前长度;A为网丝的当前截面面积。

(5)

式(5)中:εe为弹性应变。

根据式(1)～式(5)对网丝拉伸物理试验数据进行处理后得到材料塑性参数,如表1所示。采用表1中的真实应力σt和塑性应变εp赋予材料属性,进行单根网丝的拉伸数值模拟后得到应力-应变曲线,如图5所示。图5中数值模拟与物理试验结果吻合程度非常高,说明材料的弹塑性参数设置正确。

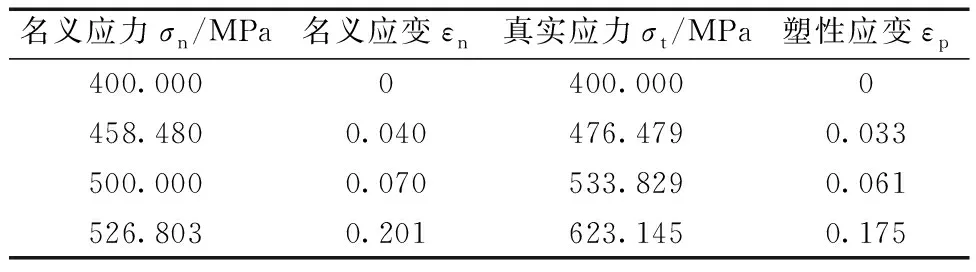
表1 网丝材料塑性参数Table 1 Plasticity parameters of wire material

3 结果与讨论

3.1 数值试验可靠性分析

所依托的网片拉伸试验是一个典型低加载速率下的准静态问题。准静态求解分析一般用ABAQUS/Standard算法解决,但Standard算法解决非线性问题时,往往需要很长的计算时间,甚至无法收敛到最终解。因此,采用广泛用于瞬态响应分析的ABAQUS/Explicit算法,该算法很好地改善了非线性问题的收敛性。同时,研究中采用三维8节点减缩积分六面体实体单元(C3D8R)和质量缩放功能,前者可以克服剪切自锁与模型扭曲问题,后者降低了Explicit算法的计算成本。

减缩积分单元在各个方向上的积分点数目较少,能节约计算成本。但较少的积分点数目会导致沙漏现象发生,采用伪应变能Ea进行沙漏控制。伪应变能、塑性变形耗散能、可恢复的应变能和单元扭曲控制耗散能等能量的总和为应变能Ei,伪应变能占应变能的多少是判断计算结果是否可靠的重要指标。伪应变能越大,计算结果可靠度越低。为了便于讨论,定义伪应变能与总应变能的比率为μ,如式(6)所示。根据文献[18-19],μ需控制在10%以下且越小越好。

(6)

伪应变能的大小与模型单元数量密切相关,单位体积内单元数量越多,伪应变能越小,计算结果越可靠,但计算成本也会急剧上升。表2列出了5种计算工况下的单元数量和计算耗时情况,可以看出,随着单位体积内单元数量的增加,单位耗时基本呈线性增加。

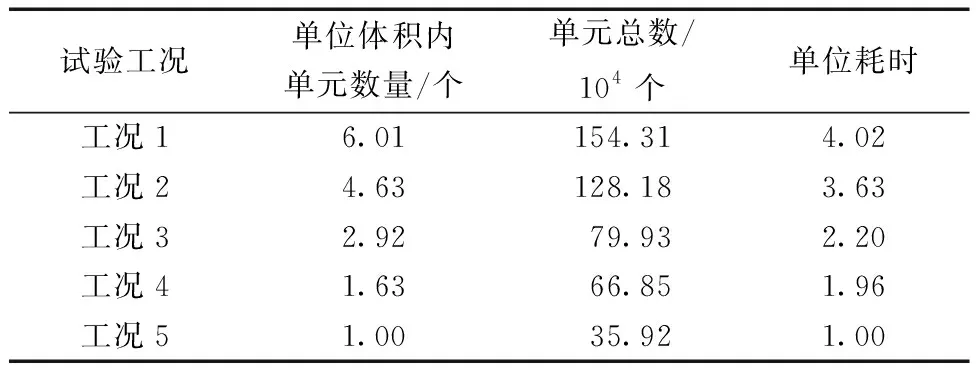
表2 数值试验工况Table 2 Numerical test conditions

网片拉伸过程中的伪应变能与应变能历程曲线如图6所示。伪应变能与应变能曲线随着拉伸率的增大呈现出相似的上升趋势。图6(a)表明,伪应变能在拉伸率到达12%前增长缓慢,之后迅速增大,至试验结束时依然保持较大的增长速率。造成这种现象的原因是:试验开始阶段的单元变形较小,沙漏不明显;但随着网片被逐渐拉长,单元扭曲变形增大,导致伪应变能急剧增加。此外,工况5～工况1随单元细分伪应变能逐渐减小,且增长幅度亦逐渐降低,工况5与工况1的伪应变能在试验结束时最大相差了115 J。同时,由图6(b)可知,各工况下应变能变化趋势大致相同。应变能在拉伸率到达10%前增长较慢,之后快速增长。但在试验结束前,由于网丝断裂后应力重分布,应变能呈现出减小再增加的波动状态。

能量比率μ变化如图7所示。试验伊始,荷载的施加使μ曲线呈现出激增又下跌的起伏现象;之后,μ稍微增加并保持稳定,直至拉伸率为11%时曲线发生波动;拉伸率达到17%时网丝失效,曲线增幅变大。虽然各工况下曲线发展趋势相近,但能量比率的平均值差别较大。随着单元的细分,能量比率的平均值从工况5的9%降低至工况1的2.5%,整体呈递减趋势;虽然工况3与工况4的能量比率曲线基本重合,但这属于特殊情况。分析整体试验情况,细分单元是减小伪应变能的一种可靠手段。此外,工况2与工况1平均值相差仅为0.5%,但随着单元总数的增加,计算成本会急剧上升,故在保持较低计算成本的情况下工况2的单元划分方式有效控制了沙漏,较为合理。

图7 伪应变能与应变能比率Fig.7 Ratio of artificial to total strain energy

对质量缩放功能的必要性和可靠性进行讨论。

在Explicit算法中,算法稳定所需的时间增量可表示为

(7)

式(7)中:Le和ρ分别为元素最小特征尺寸和密度;E为元素的弹性模量。

网片拉伸过程中,荷载引起部分单元极度变形,最小特征尺寸快速减小,从而消耗极多的运算资源。通过质量缩放增大单元质量,可以提高模型的收敛性与计算效率。但质量增加导致系统动能增加,进而可能会改变网片的受力状态,影响模型计算结果的可靠性。因此,确保试验的准静态条件尤为重要。采用半自动质量缩放将最小增量步放大为0.003 s。图8展示了不同工况下网片系统的动能以及能量平衡的历程曲线。

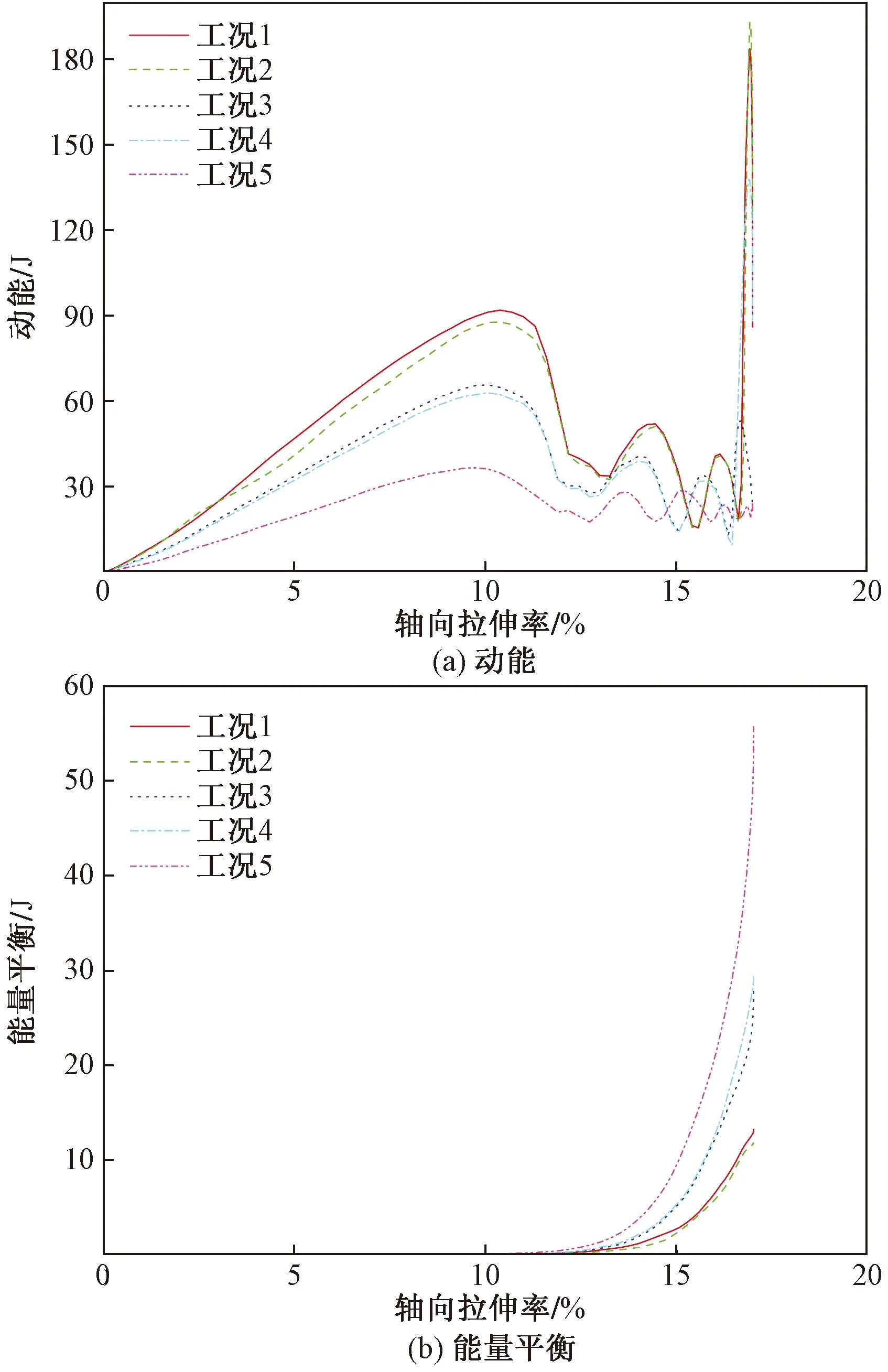
图8 动能与能量平衡历程曲线Fig.8 Kinetic energy and energy balance history

由图8(a)可知,网片系统动能在荷载施加后至10%拉伸率前先平稳增加,然后至拉伸率为17%时波动下降,该种动能历程曲线特征由平滑分析步的加载方式导致。当拉伸率达到17%时,网丝断裂失效,动能曲线呈现出急剧涨跌姿态。对比图6(b)和图8(a)可知,数值试验中动能与应变能相比几乎可以忽略不计,表明本研究中采用的质量缩放没有改变网片系统的准静态条件。

能量平衡Et为网片系统产生与耗散的能量总合,即Et=Ek+Ei-外力做的功-因质量缩放所产生的能量(Ek为动能),其历程曲线如图8(b)所示。由其定义可知,能量平衡越接近于0,则模拟过程的收敛性越好,数值模拟结果的可靠性越强。数值模拟中的能量平衡曲线在拉伸率为13%前几乎为0;当拉伸率超过13%以后,能量平衡快速增大,但试验结束时能量平衡最大数值为工况5中56 J,最小数值仅为工况1中13 J,所有工况下能量平衡与应变能的比值都可以忽略不计。因此,数值试验中的能量收敛情况良好。

综上所述,数值试验获得的结果是可靠的。

3.2 网片的轴力响应分析

数值试验得到了单轴拉伸作用下格宾网片的力学响应特征,将其与在物理试验[15]中得到的结果进行对比分析。图9给出了网片的轴力-伸长率曲线,可以看出,所有工况下轴力-伸长率曲线发展趋势基本相同,都能较好地重现格宾网片拉伸破坏过程的两个阶段,即六边形网孔机械变形阶段和网丝弹塑性变形阶段。第一阶段的伸长率小于13%,轴力与伸长率近似为线性关系且曲线斜率较平缓,网片的伸长量主要为六边形网孔机械变形与网丝弹性变形。第二阶段的伸长率为13%～17%,网孔机械变形停止,轴力-伸长率曲线仍近似为线性关系但斜率较第一阶段增大良多,网片伸长量以网丝塑性变形为主。网丝达到极限承载力后失效断裂,表现为脆性破坏和轴力呈快速回落。

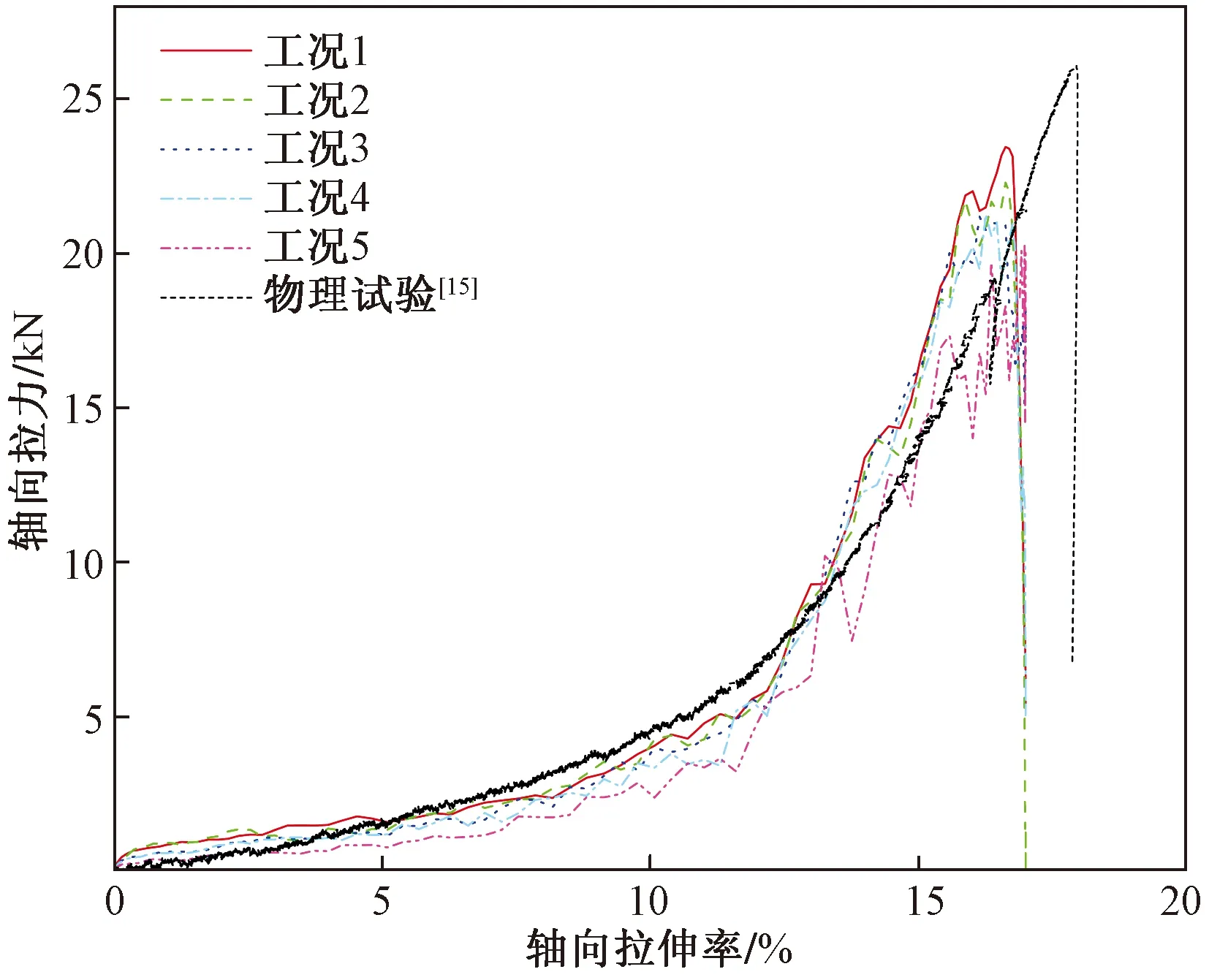
图9 网片拉伸试验轴力曲线Fig.9 Axial force curves of mesh tensile test

从峰值轴力(图9)上来看,不同工况有明显的差异。工况5轴力峰值与物理试验相差6 kN,相对误差达到了23%,且曲线波动情况明显呈锯齿状,尤其在网丝断裂前这一现象最为严重。工况5～工况1曲线发展趋势逐渐趋于平滑,轴力峰值不断增加,工况1轴力峰值与物理试验仅相差2 kN,相对误差为7%。数值试验结果得到优化的原因是单元划分逐渐精细,网片系统的伪应变能控制得到改善。数值结果表明,当采取减缩积分单元进行模拟时,需要严格控制单元大小以控制伪应变能。一旦伪应变能过大,即能量比率μ>5%时,会使模拟结果曲线波动异常和轴力误差增大。当能量比率μ<5%时,模拟结果曲线平滑且与物理试验结果较为符合。3.1节结果已表明,单元划分过细会导致计算成本急剧上升,同时模拟结果并无较大改善,因此,此类数值试验的能量比率μ可控在约5%。

由图9可知,数值试验与物理试验的最终网片拉伸率相差2%,该误差由两点导致。首先,边界条件的不同是造成这一误差的主要原因。施加拉伸荷载时,数值试验耦合端丝结点进行加载,而物理试验采用夹具夹持网片加载。夹具拉伸网片时会造成与其接触的双绞丝压缩变形,该段变形并未被记录处理,反而直接将夹具的位移距离作为网片被拉伸的绝对距离,导致计算获得的网片拉伸率大于其实际拉伸率。数值模拟试验通过耦合端丝加载,使网片整体受拉,很好地发现了这一问题,为后续物理试验的改进提供了经验:物理试验应记录网片变形前后的绝对位置以减少误差。其次,采用Explicit算法计算时会不可避免地累积误差,但在节约计算成本的条件下,这种累积误差可以接受。相较于物理试验与离散元数值模拟,有限元数值模拟更为经济快捷,且很好地揭示了网片的力学性能。

3.3 网片变形特征与应力分布

鉴于数值试验中各工况格宾网片的力学响应相似,故选择工况1的结果进行分析。图10显示了工况1中网丝失效前一时刻的状态。网片在拉伸过程中X轴方向上出现了类似“颈缩”的现象,表现为六边形网孔在宽幅方向上缩短的同时在长度方向上伸长。同时,宽幅边缘处的六边形网孔产生极大形变,网丝几乎紧贴在一起。物理试验[15]中网片的拉伸破坏情况如图11所示。对比图10与图11发现格宾网片的宏观变形特征与物理试验的宏观变形特征基本吻合。由图10可知边界约束处的钢丝应力集中现象最为严重,最大应力约为644 MPa;此外,最靠近端丝的六边形网孔开口处有较为严重的应力集中,约为600 MPa;页面网丝的应力平均为300 MPa。

图10 网片拉伸数值试验应力云图Fig.10 Numerical tensile test stress diagram

图11 网片拉伸物理试验的变形破坏Fig.11 Tensile deformation failure of gabion mesh

数值试验中网片的应力分布情况与网丝断裂位置相对应。图12给出了网丝断裂时刻的变形图以及各模拟工况下网丝的断裂情况。网丝断裂位置都位于应力集中现象最严重的边界约束处。其中,工况4和5仅有一个断裂点位于网片右侧,工况1和2则同时有两个断裂点位于网片左侧,在工况3中有4个点处的网丝同时断裂。这种网丝失效模式也体现在物理试验中,但不同的是物理试验中与夹具相连的六边形网孔开口处也时常断裂。数值试验和物理试验结果存在上述差异的主要原因归纳如下:一方面,数值模拟的各项条件过于理想,故断裂位置集中在应力集中最严重处;另一方面,物理试验中网丝材料性能、网片制作过程等存在的差异使得有较严重应力集中的六边形开口处也较易断裂。