基于岩屑分形理论的岩石力学参数实时评价方法

2023-12-14徐声驰杨虎李立常小龙刘锐周鹏高

科学技术与工程 2023年32期

徐声驰, 杨虎, 李立, 常小龙, 刘锐, 周鹏高

(1.中国石油西部钻探工程有限公司地质研究院, 克拉玛依 834000; 2.中国石油大学(北京)克拉玛依校区, 克拉玛依 834000;3.克拉玛依职业技术学院, 克拉玛依 834000)

众所周知,岩石力学贯穿于整个石油天然气勘探开发全过程。岩石的力学性质研究和应用越来越受到石油工程界的高度重视。快速、准确获取岩石力学参数对于钻完井和油气田开发工程具有重要意义。目前,获取岩石力学参数的方法包括:利用岩心开展室内力学测试,获得若干个深度点的岩心力学参数;依据统计学方法建立研究工区的多口井测井数据与岩心测试力学参数的多元回归关系式,借助专业软件由完钻井测井数据反演出岩石力学参数。该方法依赖于钻井取心情况,且需要等待完井电测之后才能计算岩石力学参数,具有较大的时效限制[1-2]。

分形理论是一门描述自然界中不规则、无序的现象和事物不规则程度的科学,研究对象为一些具有自相似性的不规则曲线和形状[3-4]。分形几何学基本思想认为,客观事物的层次结构,局部与整体方面,在时间、空间、功能、形态、信息、等方面具有统计意义上的相似性,称为自相似性。放大或缩小几何对象,可看到局部和整体具有相似的结构。维数是度量几何对象的重要特征量,是描述空间位置所需的独立坐标数目。分形理论引入了维数概念,可以定量描述客观事物的“非规则”程度,并将维数从整数扩大到分数,从而突破了一般拓扑集维数为整数的界限。

通过测量无序或不规则事物的维数,进而研究维数与某些关键参数、信息之间的内涵关系,是分形理论具体应用的主要方式[3-6]。自20世纪70年代以来,分形理论在地理学、计算机、材料科学、物理学、岩石力学等诸多领域得到广泛应用[5-7]。同时,中国多位学者在分形岩石力学领域也开展了有效探索。谢和平[8-9]率先将分形几何理论应用到岩石力学中,主要集中研究断裂演示与分形维数的关系问题,其后又将分形理论应用于岩石力学的其他领域中。李士斌等[10-12]利用分形几何理论研究了钻井过程中岩石破碎机理及形成过程,提出了一种以岩屑为对象的岩石可钻性测试方法。李玮等[13]从等破碎概率角度研究了上返岩屑分布规律问题,应用分形几何理论建立了等概率条件下上返岩屑的破碎规律表征模型。潘德元等[14]总结了岩屑分形规律的影响因素及影响程度。闫铁等[15-17]通过分析岩屑的分形破碎特征及钻井工况特点,建立钻井工程能效评价模型,研究钻井工程中破岩能耗与岩屑分形破碎特征的关系。李嵬岩[18]应用岩屑分形理论与修正钻速方程,预测了伊拉克鲁迈拉油田石膏夹层岩石可钻性。

上述学者的研究主要集中于岩石破碎分形规律和钻头可钻性评价方面,而将分形理论用于深层岩石力学参数评价的成果鲜有报道。因此,如何借助分形理论探索岩屑分形几何参数与岩石本体力学参数的关系,并将钻井期间录井岩屑进行分形测试,建立岩石力学参数的随钻评价方法,是研究的创新之处。首先,以准噶尔盆地玛湖油田为研究对象,利用完钻井岩心开展力学测试,建立岩石力学参数与多项测井物理量多元统计学模型。其次,借鉴文献[13-15]建立的岩屑颗粒的分形维数测试方法,测试目标井上返岩屑及岩心二次破碎样品的分形维数,并依据测井岩石力学模型计算出岩屑原位地层的岩石力学参数,将这些力学参数与岩屑分形维数建立统计模型。最后,建立目标油田或地区岩石力学参数的随钻评价流程,测试正钻井上返岩屑的分形维数,可实时计算正钻井段的岩石力学参数。应用案例的数据对比表明,岩屑分形维数计算的岩石力学参数具有较高的精度。研究成果拓展了分形岩石力学的应用领域,为岩石力学参数的实时预测提供了新方法。

1 岩石力学测井反演模型构建

1.1 岩心力学测试

实验采用的MTS岩石物理力学测试系统由数字电液伺服刚性试验机、孔隙度和渗透率测试、超声波测试3个子系统构成。其轴向压力、围压以及流体注入压力最大值分别为1 000 kN、140 MPa和70 MPa,轴向压力和围压的加载速率小于20 N/s,轴向位移传感器量程为-50～50 mm,位移分辨精度为0.000 1 mm。系统可同时测试力学(轴向应变、径向应变、位移、轴压、流体注压、围压)、声学(纵波和横波速度、初至时间)和温度等物理量,可获取的力学参数包括抗拉强度、单轴抗压强度、内摩擦系数(或内摩擦角)、内聚力、杨氏模量和泊松比等。

根据玛湖油田完钻井取心情况,选取Ma139、Ma15等4口井的全直径岩心,在全直径岩心同一深度处钻取3块岩心制作成3块标准岩样,共制作102块标准岩样(图1)。

图1 岩石力学测试筛选的标准岩样Fig.1 Standard rock samples for rock experimental test

选取同一深度处的3块标准岩样为一个岩样组,共计10个岩样组,编号依次为1,2,…,10。选取的岩性具有多样性和代表性,包括砾岩、泥岩、砂岩。每组标准岩样开展单轴和三轴力学压缩破坏测试,围压分别为0、20、40 MPa;力学测试后基于莫尔-库伦准则开展力学参数分析,可获得岩心的抗压强度、杨氏模量、泊松比、内聚力和内摩擦系数(表1)。

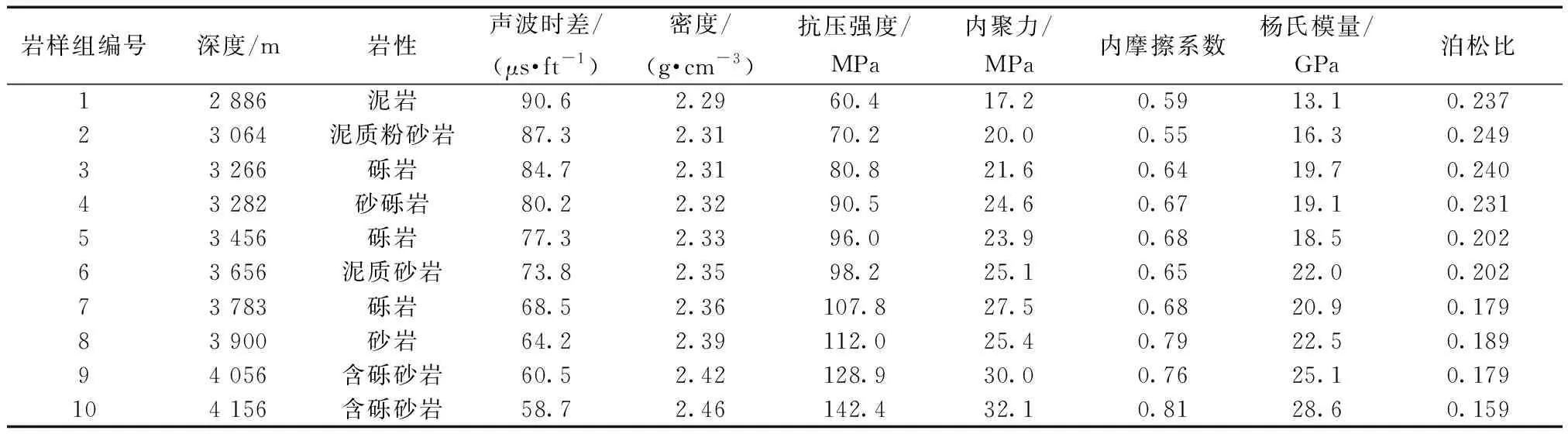
表1 玛湖油田岩心力学测试结果Table 1 Mechanical test results of core in Mahu oil field

1.2 统计学模型构建

岩石力学参数与测井物理量中的声波速度、密度之间具有较好的相关性,但中外学者针对特定地区或地层建立的岩石力学参数的测井反演关系式不具有通用性[19-20]。需要将目标油区岩心测试数据与岩样原位测井物理量对应,应用多元回归方法,建立目标油区岩石力学参数的测井统计学模型[21-22]。

由此,根据玛湖油田岩心力学测试结果,构建出适于玛湖油田的岩石力学参数测井模型(表2)。其中,单轴抗压强度与纵波时差和岩石密度的相关性最好,内摩擦系数(内摩擦角)与纵波速度相关性最好,动态杨氏模量由岩石密度、纵横波速度的理论公式计算,动、静态杨氏模量之间具有呈良好的幂函数关系,动、静态泊松比大小呈随机关系且相关性较差。

表2 玛湖油田岩石力学参数与测井数据的关系Table 2 Relationship between rock mechanical parameters and logging data in Mahu oil field

2 岩石破碎的块度分形维数

岩石结构中充满随机的、无序的缺陷,岩石是一种具有天然损伤的复杂地质材料。钻井岩石破碎过程受岩石内部结构和钻头的作用力控制。由于岩石本身以及载荷的各向异性,岩石破碎形态表现的千差万别[23-24]。岩石中小破裂群体逐渐聚集,形成宏观上的破碎,这种从微观损伤发展到宏观破碎的过程是能量耗散过程。由于小破裂又是由更微小的裂隙演化和聚集而来,这种自相似的行为必然导致破碎后块度分布也具有自相似的特征。因此,破碎岩屑还是存在内在的统一性,其自相似性在统计意义上仍然成立。

2.1 岩石的分形维数

岩石经钻头破坏后形成形态各异的岩屑颗粒,但从统计中仍满足自相似规律,现常用Rosin-Rammler函数[式(1)]和Gaudin-Schuhmann函数[式(2)]描述岩屑颗粒分布规律[11]。

(1)

(2)

式中:N为岩屑粒度小于γ的相对累积量,%;γ为岩屑颗粒直径,mm;γm为岩屑粒度分布直线与N=1直线交点的相对累积量值;γ0为粒度特性系数;n为均匀性系数。

将式(1)按级数展开后,舍去第二项后面多项,即可得到式(2),表明当岩屑粒度较小时,两个分布函数均可用于岩屑颗粒分布规律,研究认为式(1)适用于颗粒分布趋于粗粒端,式(2)适用于颗粒分布趋于细粒端[10-12]。

将标注化处理后岩屑通过不同方形孔筛网筛选,孔径记为γi,筛子孔径选取大于5种,以获得足够的数据量用于回归分析。以筛选粒径小于γi的岩屑样品被筛选漏下去,颗粒质量记为Mdown(γi),对应的留在筛网上的记为M(γi),颗粒总数记N(γi),称重天平量程为0～250 g,精度为0.001 g。

岩屑样品二次破碎后粒度分布遵循质量-频率分布关系可表示为

(3)

对式(3)两边求导有

dM∝γn-1dγ

(4)

将岩屑破碎后定义为一种破碎体分形,可表示为

N(γi)=Aγ-D

(5)

考虑破碎体质量-尺寸-数量间关系为[18]

(6)

由式(5)和式(6)可知,岩屑质量和颗粒直径关系为

dM∝γ3dN

(7)

由式(4)和式(7)可得

γn-1dγ∝γ3γ-D-1dγ

(8)

因此,由式(8)可得到分形维数D的表达式为

D=3-n

(9)

式中:γmax为岩屑最大粒径,mm;M为岩屑总质量,g;A为常数;D为分形维数,无量纲;V为岩屑颗粒体积,mm3。

2.2 岩心分形维数测试

采用型号ST-E200的颚式岩石破碎机,对上述10组标准岩样进行力学测试后的碎块进行二次破碎处理。该破碎机由动和静两块颚板组成破碎腔,广泛运用于各种矿石与大块物料的破碎,被破碎物料的最高抗压强度为320 MPa。破碎机工作时,活动颚板对固定颚板作周期性的往复运动,物料在两颚板间受到挤压、劈裂、冲击而被破碎。设备转子转速为100～1 000 r/min,进料口尺寸为0～80 mm,出料粒度为0～30 mm,处理能力为0.3～1.0 t/h,电机功率为6 kW。

首先,对岩心二次破碎后的岩屑进行称重;然后进行筛分,将岩屑通过不同方形孔筛网筛选,孔径记为γi(i为不同孔径),筛子孔径选取8种,把各尺寸级别的岩屑分离出来,并对各尺寸级别的岩屑进行称重并记录。

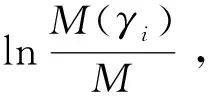
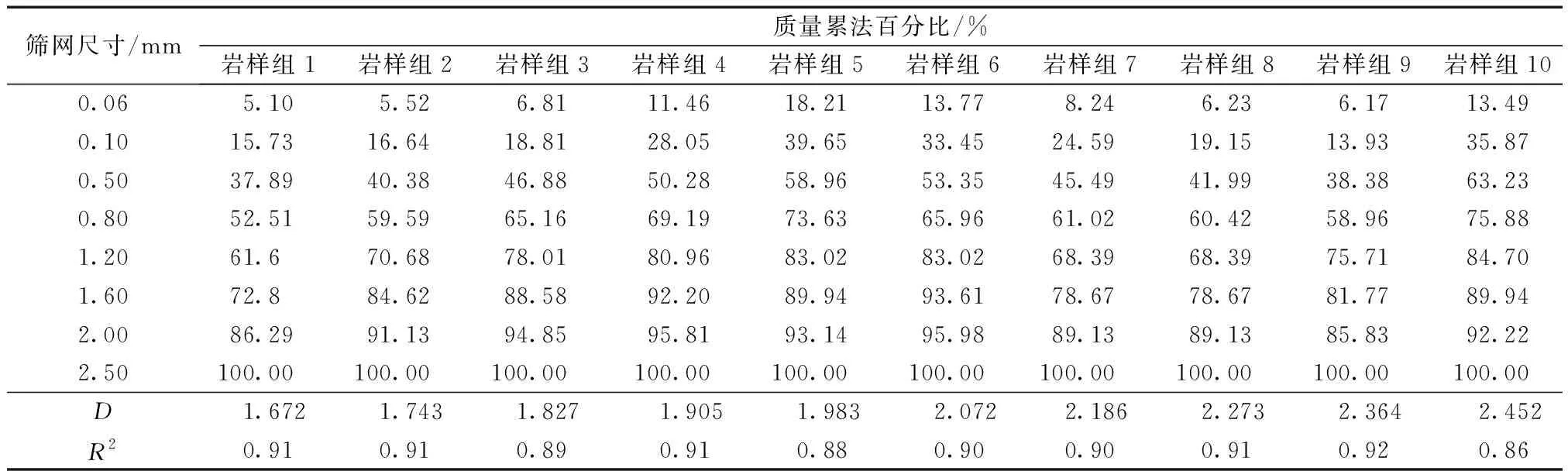
表3 岩屑筛分质量累计百分比Table 3 The cumulative percentage of screened mass of upward return cuttings

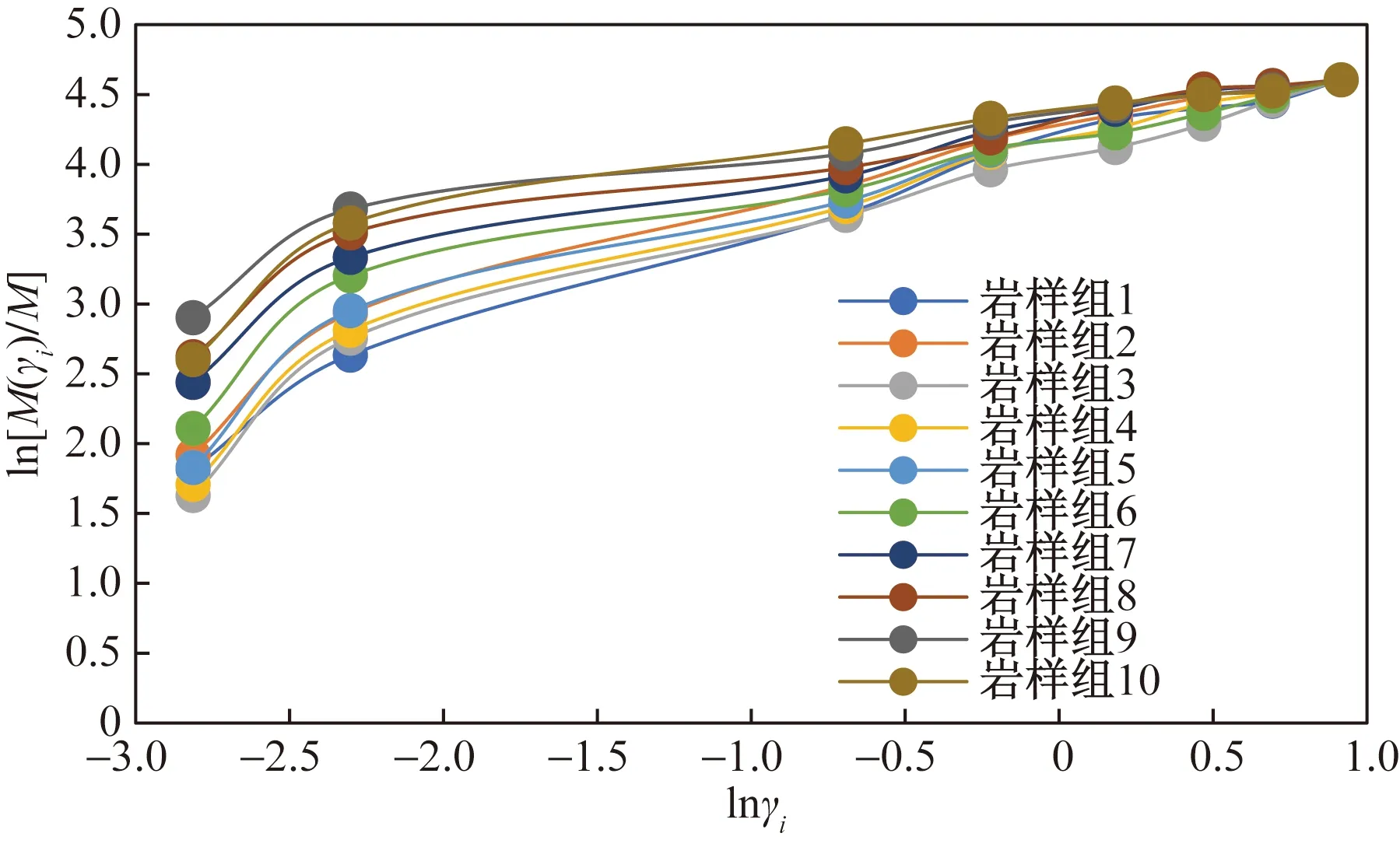
图2 岩心二次破碎样品的分形曲线Fig.2 Fractal curve of core secondary crushing sample

3 基于分形维数的岩石力学模型构建

将上述玛湖油田10组岩心力学参数的测试数据与其对应的分形维数绘制出散点图(图3),并建立各项力学参数的线性回归方程,表明岩心二次破碎颗粒的分形维数与其各力学参数的相关性较好。其中,岩石抗压强度、内摩擦系数随分形维数增大而增大,表明分形维数越大,岩石越坚硬;杨氏模量随分形维数增大而增大,泊松比随分形维数增大而减小,表明分形维数越大,岩石越难以变形。

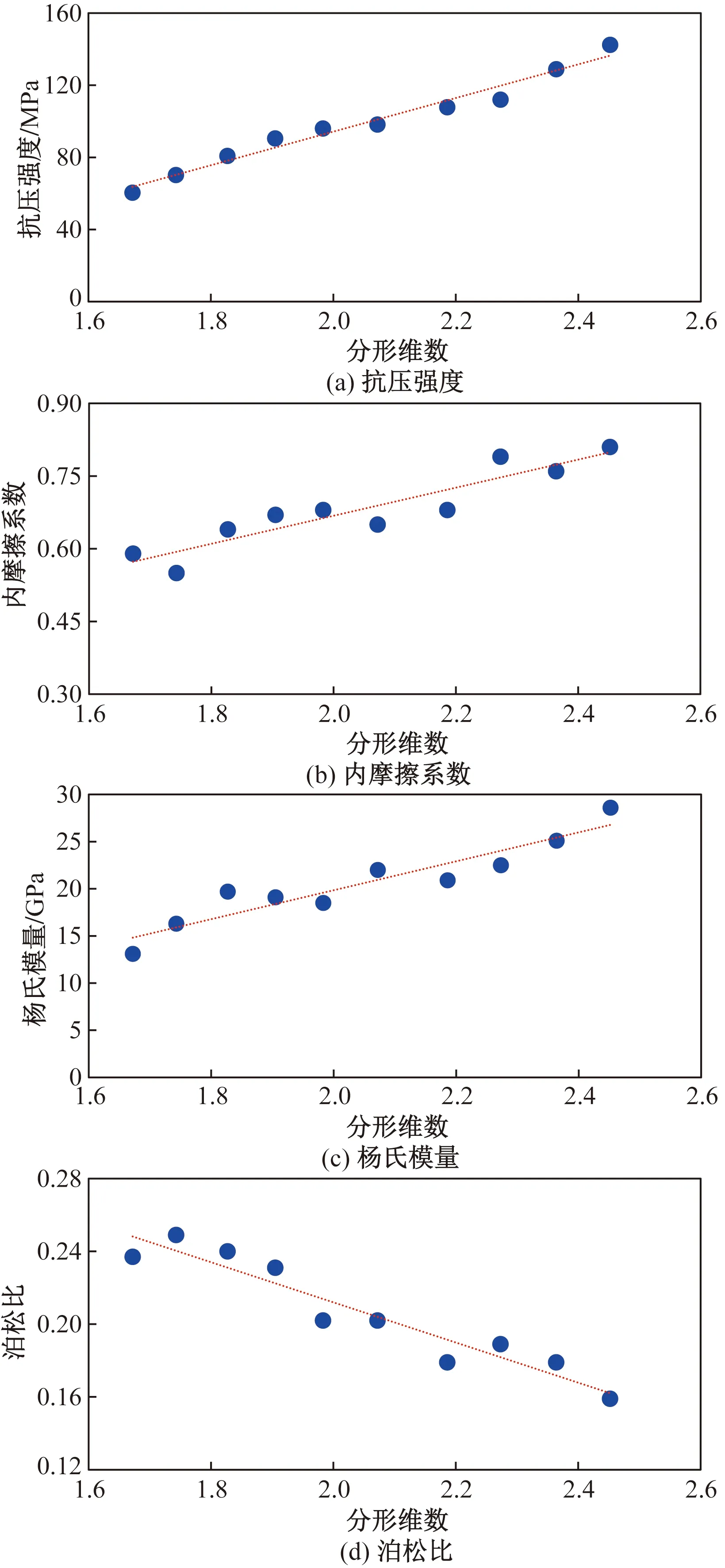
图3 岩石力学参数与分形维数的关系曲线Fig.3 Relationship curve between rock mechanical parameters and cutting’s fractal dimension

结果(图3)表明,岩石的各项力学参数均可用岩屑分形维数来表征或衡量,也表明岩屑的微观结构决定宏观的岩石物理力学性质和岩屑粒度分布。由此归纳出基于岩屑的分形维数的玛湖油田深层岩石各项力学参数随钻计算模型(表4)。

表4 玛湖油田基于岩屑分形维数的岩石力学参数模型Table 4 Rock mechanics parameter model based on fractal dimension of rock debris in Mahu oil field

4 模型验证与应用

4.1 模型验证

Ma123井是一口部署于准噶尔盆地玛湖油田的评价井,目的层为二叠系风城组,岩性主要为灰色、褐灰色砂砾岩。该井钻进到风城组后,收集井深为3 700～4 100 m共14个深度点处的岩屑,经清洗烘干,再二次破碎。将二次破碎岩屑样品用8种不同目数的筛网分选,按照2.2节中的步骤,利用上返岩屑样品的筛分质量累计百分比数据,通过线性回归计算得到分形维数(表5)。将获取的分形维数,代入表4所示的模型,得到基于岩屑分形维数的各项岩石力学参数(表6)。由此。通过录井随钻实测上返岩屑分形维数,实现了深层岩石力学参数的实时预测和评价。待Ma123井完井电测后,将该井测井数据代入表2中的模型,得到基于测井数据的各项岩石力学参数(图4)。

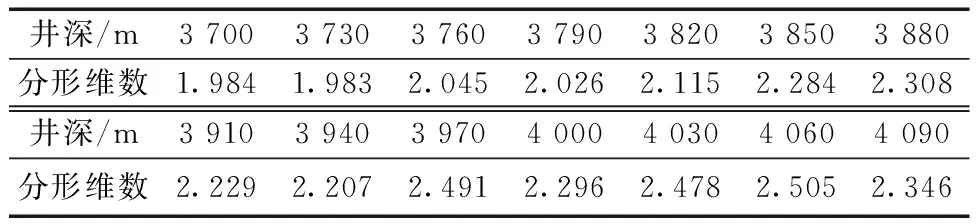
表5 Ma123井风城组岩屑分形维数Table 5 Fractal dimension of cuttings in fengcheng formation of well Ma123

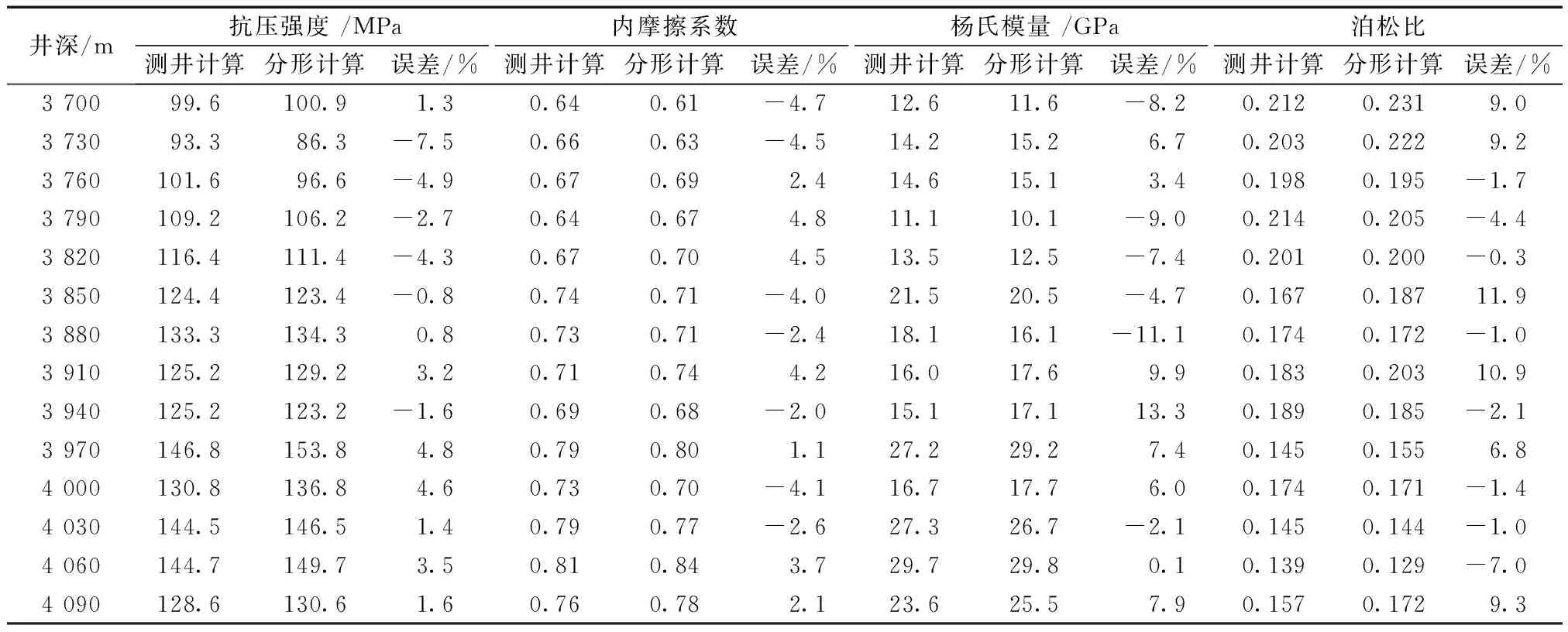
表6 分形维数与测井数据计算的岩石力学参数对比Table 6 Comparison of rockmechanical parameters calculated by fractal dimension and logging data

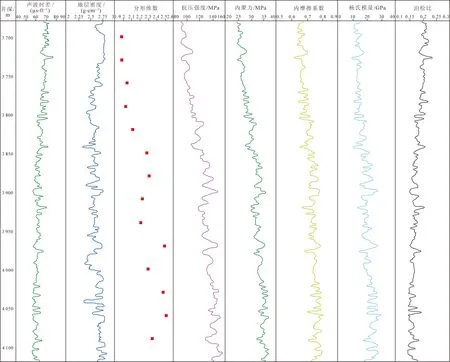
1 ft=0.304 8 m

以图4中Ma123井测井数据反演出的岩石力学参数为基准,对比由岩屑分形维数计算的岩石力学参数(表6),分形维数计算的抗压强度误差为-7.5%～4.6%,内摩擦系数误差为-4.7% ～4.8%,杨氏模量误差为-11.1%～13.3%,抗压强度误差为-7.0%～10.9%。抗压强度与内摩擦系数的误差相对较小,杨氏模量与泊松比的误差略大,可满足工程要求。结果表明,利用上返岩屑分形维数实现岩石力学参数的实时计算是可行的。

4.2 录井实时评价方法

通过Ma123井录井实践,总结出一套基于分形理论的岩石力学参数的实时评价方法:①针对特定的工区或地层,利用完钻井的岩心和对应的测井数据,测试岩石力学参数,建立岩石力学参数与测井数据的关系式;②将力学测试后的岩心碎块进行二次破碎,测试出岩屑分形维数,建立岩石力学参数与岩屑分形维数的关系式;③获取正钻井岩屑,二次破碎后并测出其分形维数,再利用岩石力学参数与岩屑分形维数的关系式,即可实时获取岩石力学参数。