换热器螺旋管冷凝换热的数值模拟与实验研究

2023-12-14徐裕民孙伟珂于哲林洪俊陈学永李西兵

科学技术与工程 2023年32期

徐裕民, 孙伟珂, 于哲, 林洪俊, 陈学永, 李西兵

(福建农林大学机电工程学院, 福州 350002)

随着工业化进程的加快,能源问题也越来越突出,中国在第75届联合国大会上宣布,力争2030年前二氧化碳排放达到峰值,努力争取2060年前实现碳中和目标[1]。在兼顾可靠性与碳中和两个目标的要求下,提高能效,注重节能技术的开发、推广及使用。换热器是一种应用非常广泛的热交换器,在能源产业中有着举足轻重的地位,换热器在整个生产工艺总设备中占据30%以上。具有单位面积换热量大,传热效率高,操作压力大,补偿性能好等优点,现广泛应用于制冷、冶金和化工等领域[2]。因此加强不同参数对螺旋管传热的影响研究对于提高换热器的节能效果非常重要。

对于换热器的冷凝换热,中外学者开展了大量工作。杨英英等[3]采用R32为工质对水平管进行可视化冷凝换热实验研究,结果表明,El Hajal J流型图对小管径内冷凝流型的预测误差较大。Mozafari等[4]开展了螺旋管换热器内R-600a的冷凝特性实验研究,结果表明,在每一倾角下,换热系数随质量流量和平均蒸汽质量的增加而增加。Macdonald等[5]对丙烷在水平管内的冷凝传热进行了实验,结果表明,传热系数随着质量流量的增加而增加,随着饱和温度的降低而降低。Salimpour等[6]讨论了结构参数对螺旋盘管中R404A冷凝传热的影响,结果表明,在低蒸汽质量下,传热系数随着盘管直径的减小而增加,随着盘管间距的增加而减小。Yu等[7]以碳氢类混合工质作为制冷剂,使用实验和模拟相结合的研究方法对螺旋管内的凝结换热开展研究,提出了一种适用于碳氢类混合工质的冷凝换热关联式。Zhu等[8]对光管和螺旋槽管两种结构中超临界CO2的换热系数进行了实验研究,结果表明,螺旋槽管具有较好的换热效率。赵进元[9]对螺旋管内二次流的换热特性进行研究,最终得到了螺旋管内强化换热技术的方法。Koluib[10]对螺旋管换热器R407-C热流体工质的冷凝换热特性进行实验研究,结果表明,R407-C的质量流量与换热系数成正比,随着R407-C饱和温度的降低,R407-C侧换热系数和整体换热系数都相应增加。曹佳铭等[11]对一种缠绕管换热器进行结构优化与实验研究,提出一整套改进的计算模型,结果表明,改进后的模型传热误差最大不超过3.6%,压降误差最大不超过8.5%,说明改进的计算模型具有较高的准确度。

综上可知,关于水平管和螺旋管冷凝传热的实验研究很多,而对换热器螺旋管的数值模拟研究很少,对螺旋管在制冷和空调热水器系统中的推广使用而言,现有研究还远远不足。为此,对R22制冷剂在螺旋管中冷凝换热进行数值模拟,分析换热器螺旋管的流场分布特性,研究流体流速和饱和温度对螺旋管内换热性能的影响,并在企业内的换热器测试实验室进行实验,对数值模拟的准确性进行验证。为螺旋管换热器的设计优化以及空调热水器一体机的节能损耗研究提供一定的科学依据。

1 数学模拟方法

1.1 数学模型

1.1.1 多相流模型控制方程

流体体积法(volume of fluid,VOF)通常可用于跟踪气液界面的运动,是一种简单有效的自由边界数值处理方法,因此选用VOF模型作为模拟设置中的多相流模型。FLUENT18.0中的VOF模型能够用于模拟不同类型管道的冷凝和流动[12]。对于多相流,在VOF模型中,αl和αv分别为液体和气体的体积分数。液体和气体的总体积分数应限制为1,即

αl+αv=1

(1)

其他热性质(如黏度和导热率)也通过上述方程所示的算术平均值来计算。能量和温度计算公式分别为

(2)

(3)

式(2)中:El为液体内能量;Ev为气体内能量;ρv为气体密度,kg/m3;ρl为液体密度,kg/m3;Tl为液体的温度,K;Tv为气体的温度,K;密度ρ的计算公式为

ρ=αlρl+αvρv

(4)

包括连续性、动量、能量守恒在内的控制方程如下[13]。

(1)连续性方程。

(5)

式(5)中:t为时间,s;∇为哈密尔顿算子;u为速度,m/s;Sl为从相变模型获得的液相质量源项,kg/(m3s)。

(6)

(2)动量守恒方程。

ρg+Fσ

(7)

式(7)中:p为压力,Pa;ɑ为相体积分数;μ为物体黏度,Pa·s;g为重力加速度,m/s2;Fσ为表面张力。由连续表面力模型计算得出[14],其计算公式为

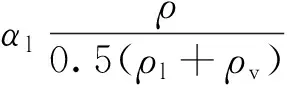
(8)

式(8)中:σ为表面张力系数;κ为曲率,其计算公式为

(9)

(3)能量守恒方程。

(10)

式(10)中:E气体和液体的总能量;T为气体和液体的总温度;λe为气液相有效热传导系数;hlg为汽化潜热。

1.1.2 相变模型

在数值研究中,Lee相变模型同时考虑了传热和传质。质量源项由Lee相变模型[15]计算。Lee相变模型与VOF模型相结合已广泛应用于管内流动冷凝的建模,VOF模型与Lee模型相结合用于模拟,以获得流型和传热系数。Lee模型中的传质可表示为

(11)

(12)

式中:Tsat为饱和温度;Tl为液体温度;Tv为气体温度;Sv为蒸发中的传质;Sl为冷凝中的传质;r为松弛因子;ρl和ρv分别为液相和气相密度,eva为蒸发,con为冷凝。

Lee相变模型中的松弛因子r对模拟结果有较大的影响[16]。因此,为了提高收敛速度和精度,在冷凝换热的数值模拟中,r值取103。

1.1.3 湍流模型

使用可以旋流校正的“Realizablek-ε模型”对湍流条件下换热器螺旋管的管内流场进行数值仿真能更好的适应曲率变化,而且可以加快收敛速度。“Realizablek-ε模型”的湍动能k的表达式为[17-18]

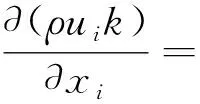
(13)

式(13)中:σk为湍动能的湍流普朗特数;xi为X轴方向坐标分量;ui、uj为X、Y轴方向速度分量。。

湍流耗散率ε的表达式为

(14)

式(14)中:C1、C2为经验常数;xj为Y轴方向坐标分量;σε为耗散率的湍流普朗特数。

湍流黏性系数μt可表示为

(15)

式(15)中:Cμ为常数。

1.2 物理模型

采用Solidworks2018三维软件构建了换热器螺旋管的物理模型,重要的结构参数主要有换热器螺旋管的螺旋直径D、螺距P和管道直径d,如图1所示。利用ICEM CFD18.0软件对换热器螺旋管物理模型进行网格划分,换热器螺旋管的进口端面的网格,如图2所示,通过FLUENT18.0软件对换热器螺旋管的物理模型进行数值仿真。

图1 螺旋管三维结构示意图Fig.1 Schematic diagram of three dimensional structure of spiral tube

图2 进口面网格示意图Fig.2 Grid diagram of inlet surface

1.3 数值方法

数值模拟中考虑了重力的影响,重力加速度方向是沿Z轴负方向。换热器螺旋管的管内工质为R22制冷剂,计算域内的工质物性可由REFPROP9.1确定。在螺旋管的进口处设置速度入口边界条件,螺旋管进口温度设置为323.15 K;在螺旋管的出口处设置压力出口边界条件;设置入口螺旋管内的气相体积分数为1;换热器螺旋管的壁面设置为无滑移壁面,材料为不锈钢,由于定壁温或者定热流等壁面边界条件对压降和换热无影响[19],因此螺旋管壁面设置为定壁温无滑移壁面,壁面温度设置为313.15 K,与饱和温度差值10 K,输入相应的水力直径和湍流强度。

在FLUENT软件中,采用Transient求解计算器,Explicit格式离散求解。采用Implicity Body Force处理提高计算收敛性。湍流模型选用Realizablek-ε模型,选择Scalable Wall Functions来处理湍流模型的边界层。求解计算过程采用SIMPLE算法;梯度离散项采用Least Squares Cell Based;压力离散项采用PRESTO!;体积分数项采用Geo-Reconstruction;动量方程、能量方程、湍流动能方程和耗散率方程采用二阶迎风格式;松弛因子不变,使用默认值,对管道出口处气相体积分数、进出口质量流量进行监控,保证数值模拟达到收敛。

2 数值模拟结果与分析

2.1 网格无关性验证

网格无关性验证将选取结构参数为螺旋直径D=300 mm、螺距P=19.52 mm、管道直径d=9.52 mm的换热器螺旋管,对螺旋管的物理模型采用O型结构化网格划分,并且对边界层处的网格进行加密,表1为相应的网格设置参数与网格数量。

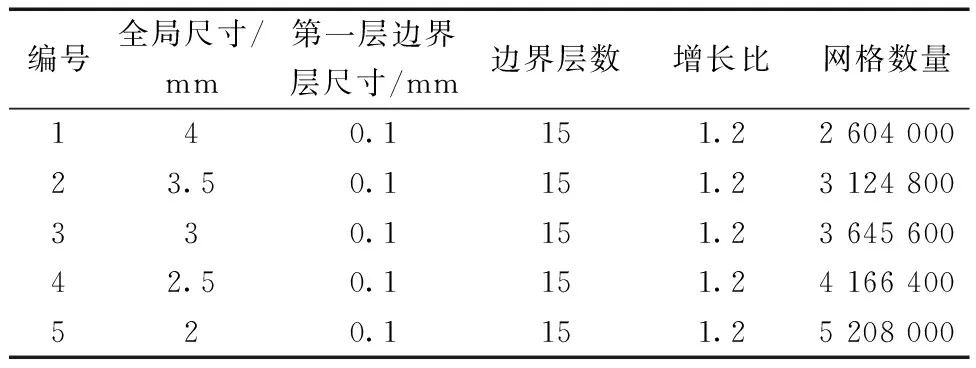
表1 网格划分参数及输出网格数Table 1 Mesh partition parameters and output mesh number

网格无关性验证基于FLUENT18.0软件进行分析,在软件中设置条件为:工质为水,进口速度为1 m/s,进口温度为298.15 K,在恒壁温的条件下,壁面温度为333.15 K。换热系数和进出口压降随网格数量的变化分别如图3(a)和图3(b)所示。

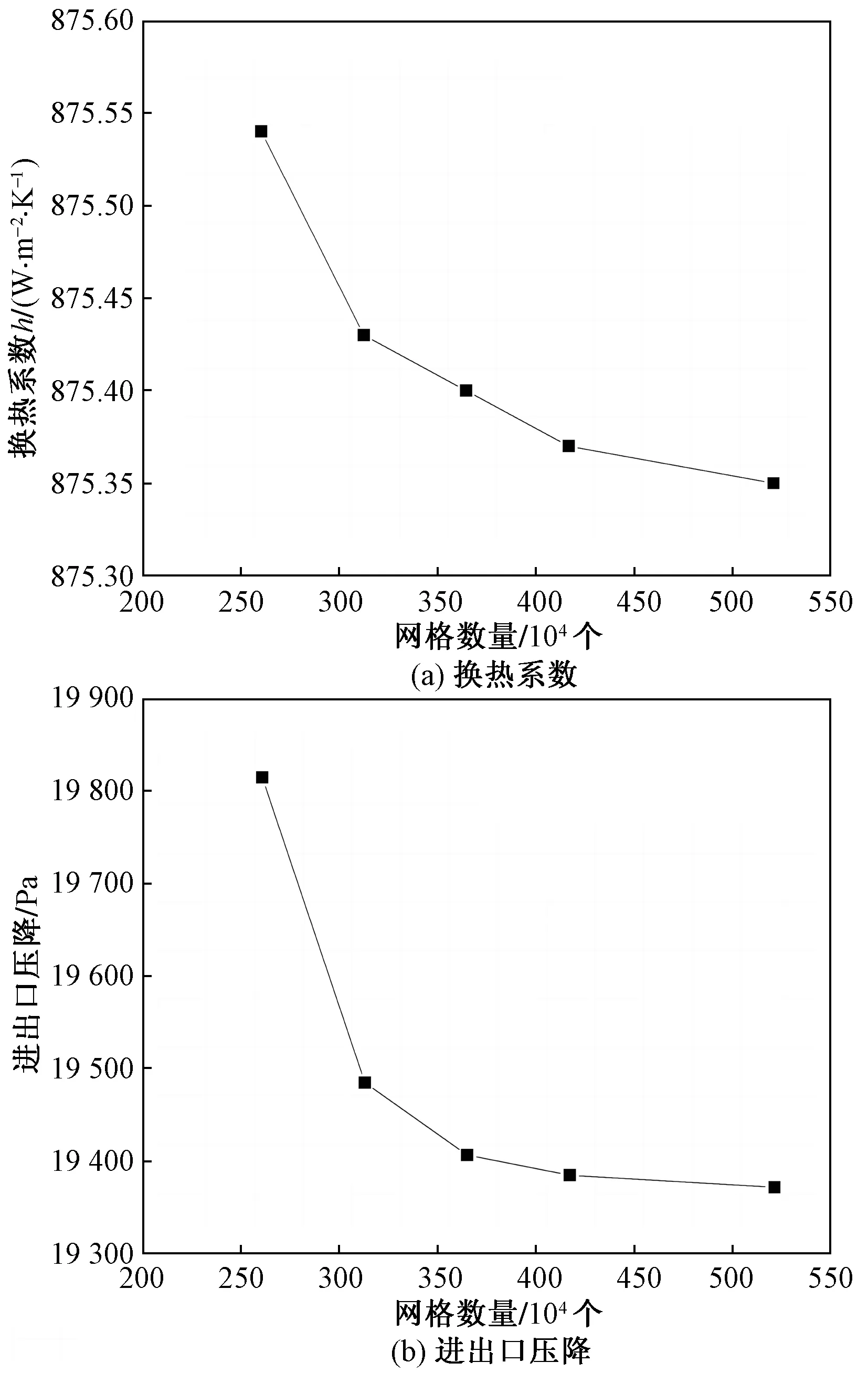
图3 换热系数和进出口总压降随网格数量的变化示意图Fig.3 Schematic diagram of wall heat transfer coefficient and total pressure drop at inlet and outlet with the number of grids

数值仿真结果表明,换热器螺旋管的换热系数、进出口压降随网格数量增加而减少;当网格数量为4 166 400的情况下,换热器螺旋管的换热系数和进出口压降的变化趋于平稳,将不随网格的变化而变化。因此从计算精度和效率两方面考虑,采用第4组划分网格的方法,这种划分网格的方法可以满足网格无关性验证的要求,对其它螺旋管进行网格划分时,均可使用类似的方法计算。

2.2 各参数沿管截面分布情况

2.2.1 螺旋管内气液相体积分布情况

图4为流体在螺旋管内沿着轴向方向上,是ZX截面的气液相分布云图。

1#～22#为螺旋管入口开始每180°的截面

R22制冷剂在螺旋管内的冷凝过程中,随着气态R22制冷剂的不断凝结,冷凝液逐渐积累,管内的冷凝流型开始改变。从图4可以看出,沿管道方向冷凝液越来越多,主要流型为分层流。因为入口边界条件为纯气相,冷凝时间非常短暂,因此,入口阶段流型为雾状流。随着气态R22释放潜热,在管壁附近持续冷凝,在剪切力的影响下,冷凝液被管道中心流速较快的气体吹起,由于剪切力大于重力,因此,冷凝液沿着螺旋管外壁流动,形成半环状流,随着冷凝过程的继续进行,流型逐渐由半环状流转化成分层流,在分层流流型中,由于液相密度较大,速度也相应减小,流型在重力的作用下,冷凝液聚集在管道底部。此外,还可以看出气液界面略微倾斜,这是由于离心力导致的。

2.2.2 螺旋管内温度场分布情况

图5为流体在螺旋管内沿着轴向方向上并且是ZX截面的温度场分布云图。

1#～22#为螺旋管入口开始每180°的截面

将螺旋管的温度场与气液相分布云图相对比,螺旋管管内温度场与气液相分布场情况对应良好,从图5可以看出,入口处全部为高温的气态工质,管壁温度低于制冷剂温度发生冷凝,冷凝换热发生不久后,螺旋管外壁开始出现一层液膜,因此管壁附近温度较低。随着气态R22制冷剂在螺旋管内发生持续性的冷凝,在重力和离心力的双重影响下,管道上部的冷凝液开始流向管道的外侧底部,并且冷凝液逐渐增多,导致管底的温度比较低。因此,与管道顶部相比,管道底部有很明显的温度边界层。

2.2.3 螺旋管内速度场分布情况

图6为流体在螺旋管内沿着轴向方向上并且是ZX截面的温度场分布云图。

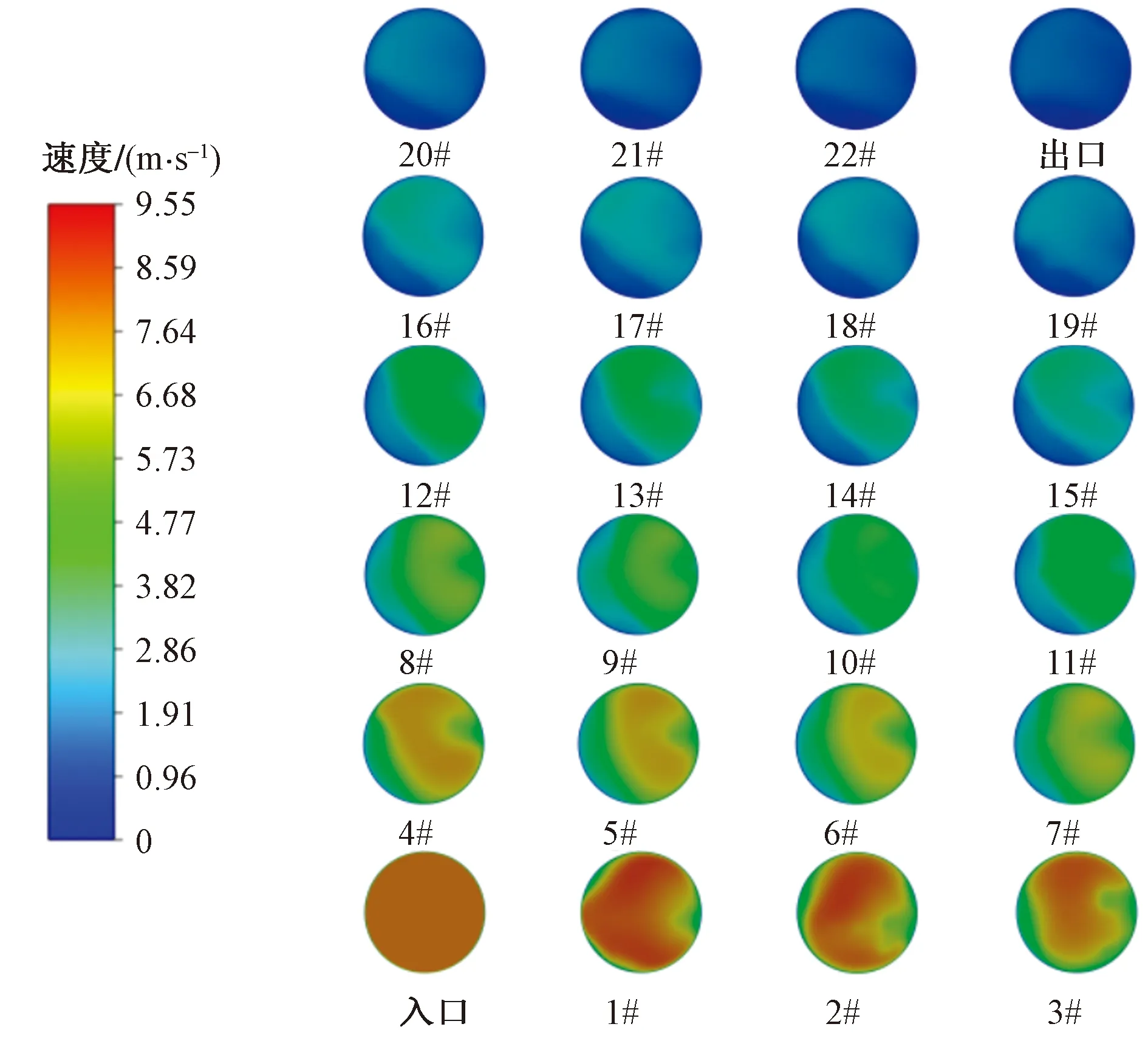
1#～22#为螺旋管入口开始每180°的截面

从图6中可以看出,流体速度沿着管道流动方向逐渐减小,这是因为随着冷凝换热地进行,冷凝液逐渐增多,流体密度逐渐增大,整体流速也就逐渐减小,并且液相部分的速度小于气相部分的速度。此外,在螺旋管的上端和下端流体的流速则是近似对称的,并且速度分布没有明显的变化,由于离心力和二次回流的作用,截面外侧的流速要大于内侧的流速,外侧管壁附近具有较大的速度梯度,管内侧的速度等值线呈以内侧顶点为中心的小的凸起状。

2.3 螺旋管内冷凝换热影响因素

2.3.1 流体流速对换热系数的影响

图7为在饱和温度323.15 K下,螺旋管内不同流体流速6、8、10 m/s时冷凝换热系数随干度的变化趋势图。从图7中可以看出,在饱和温度和干度一样的条件下,流体流速越高,冷凝换热系数越大。因为随着流体流速增高,气液界面的剪切力越大,增加了界面扰动,促进了液膜中的湍流强度,强化了气相和液相之间的换热,使得冷凝换热系数增大。此外,在相同速度的条件下,干度越大,换热系数也相应增大。因为干度增加,说明螺旋管道的截面有很大一部分为气相,液相部分占据的较少,冷凝液的厚度随着干度的增加而减小,其中的热阻也相应减小,因此使得换热系数增加。

Tsat为饱和温度;v为流体速度

2.3.2 饱和温度对换热系数的影响

图8为流体流速在8 m/s下,螺旋管内不同饱和温度303.15、313.15、323.15 K时冷凝换热系数随干度的变化趋势图。从图8中可以看出,饱和温度对冷凝换热系数有很大的影响,随着饱和温度降低,冷凝换热系数相应增大,因为在不同的饱和温度时R22制冷剂有着不同的物理性质,饱和温度越低时,R22制冷剂释放出的潜热越高,换热系数越大。另外,随着饱和温度的增高,液相密度减小,而气相密度增大,气液相密度的改变会造成气体空隙率降低,让管道截面上更大一部分被液相占据,产生非常大热阻,从而使得冷凝换热系数降低。R22制冷剂在303.15、313.15、323.15 K时的热力学性质使用物性软件REFPROP9.1查询,R22制冷剂的物性参数如表2所示,汽化潜热由标准状态焓与摩尔质量计算,计算公式为[20]

表2 液相R22和气相R22在各饱和温度下的热物性参数Table 2 Thermophysical parameters of liquid phase R22 and gas phase R22 at various saturation temperatures

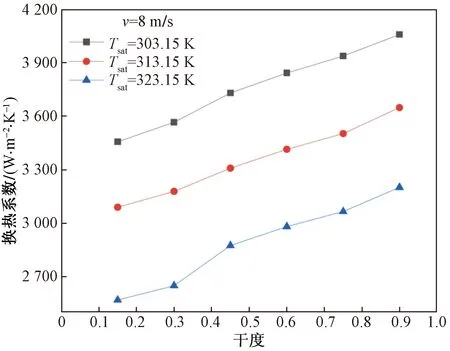
图8 饱和温度对冷凝换热系数的影响Fig.8 Influence of saturation temperature on heat transfer coefficient of condensation

(16)

式(16)中:L为汽化潜热,J/kg;H为标准状态焓,J/kmol;M为摩尔质量,kg/kmol。

从表2中还可以看出,在液相状态下,随着饱和温度增高,液体的黏度降低,使得液体的导热能力升高,有助于提高螺旋管的换热性能,但是液相热阻对换热系数影响更大。因此,在饱和温度升高时,整体的冷凝换热系数降低。

3 实验研究

3.1 实验系统原理

本次实验为螺旋管管内冷凝传热实验,实验的主要目的是为了对不同因素下螺旋管内冷凝换热系数进行测量,从而对数值模拟结果进行验证。采用R22制冷剂作为冷凝换热的工质,在常压的工况下运行。将不锈钢制作的螺旋管作为研究对象,实验系统原理如图9所示,主要由R22制冷剂回路、冷却水回路和相关测试装置以及数据测量系统组成。

图9 实验原理图Fig.9 Experimental schematic diagram

制冷剂系统主要包括压缩机、循环泵、螺旋管实验段、储液罐、过滤阀、流量计、膨胀阀、蒸发器、气液分离器和稳压器,流量计置于过滤阀与膨胀阀之间对制冷剂的流量进行测量。压缩机排出的高温、高压的气态R22制冷剂进入换热器螺旋管实验段,与注入生活水箱中的冷水进行换热,发生冷凝产生冷凝液流进储液罐中,被干燥、计量后经膨胀阀节流进入蒸发器,吸收周围环境的热量,再经过气液分离器,变为气态制冷剂后被压缩机吸入,进入下一次循环。同时,在螺旋管实验段的进出口分别插入PT100温度传感器和压力传感器对R22的温度和压力进行测量。并且通过流量计测量R22体积流量计算速度。

实验整体装置如图10所示,实验将选取结构参数为螺旋直径D=300 mm、螺距P=19.52 mm、管道直径d=9.52 mm的换热器螺旋管。为了降低环境温度所产生的误差,所有实验设备和管道表面使用了隔热保温措施。

图10 实验实物图Fig.10 Actual picture of experiment

3.2 实验数据处理

实验过程中保持螺旋管外壁面温度为恒定值,通过调节流量大小,再基于螺旋管进出口温度和压力,计算出螺旋管的壁面平均热流密度q,在相变情况下q的计算公式为[21]

(17)

式(17)中:m为质量,kg;l为螺旋管长度,mm;ΔH为螺旋管进出口焓差,J/kmol。

螺旋管实验段进口干度可表示为

(18)

螺旋管实验段出口干度可表示为

(19)

式中:xin、xout分别为进口和出口的干度;U为加热电压,V;I为加热电流,A;Q为冷凝放热量,W;hs为R22处于饱和液态时的比焓,J/kg;hin为预热前过冷液态时的比焓,J/kg;mr为制冷剂测质量流量,kg/h。

R22制冷剂的平均干度可表示为

(20)

R22制冷剂的饱和温度可表示为

(21)

式(21)中:Tin、Tout分别为R22制冷剂进出口温度,K。

螺旋管内冷凝换热系数的计算公式为[22-23]

(22)

式(22)中:hex为R22制冷剂的冷凝换热系数,W/(m2·K);δw为管壁厚度,mm;Tw为壁面温度,K;λ为螺旋管的导热系数,W/(m·K)。

3.3 数值模拟结果与实验结果对比分析

将模拟数据与实验数据进行对比,并判断数值模拟模型的合理性。

3.3.1 不同流体流速下冷凝换热模拟数据与实验数据对比

图11描述了流体流速分别为6、8、10 m/s,饱和温度323.15 K的条件下,数值模拟和实验得到的冷凝换热系数对比情况。从图11中可以看出,流体流速模拟数据和实验数据对冷凝换热换热系数的影响的趋势较为一致,冷凝换热系数在模拟数据整体上比实验数据偏高,流体流速为6 m/s时,最大误差在11%,平均相对误差为7.02%,流体流速为8 m/s时,最大误差在10.8%,平均相对误差为5%,流体流速为10 m/s时,最大误差在7.02%,平均相对误差为4.7%,流速越大时,误差较小,因为在流体流速较大时,传热传质得到强化,换热的损失量较小。

图11 不同流体流速时冷凝换热系数模拟值与实验值的对比Fig.11 Comparison of simulated and experimental values of condensation heat transfer coefficient at different flow rates

3.3.2 不同饱和温度下冷凝换热模拟数据与实验数据对比

图12给出了在流体流速8 m/s,饱和温度分别为303.15、313.15、323.15 K时,数值模拟和实验得到的冷凝换热系数对比情况。模拟数据和实验数据均表明,R22在303.15 K时的冷凝换热系数整体上高于323.15 K的冷凝换热系数。饱和温度为303.15K时,最大误差在3.26%,平均相对误差为1.84%,饱和温度为313.15 K时,最大误差在6.05%,平均相对误差为3.1%,饱和温度为323.15 K时,最大误差在8.11%,平均相对误差为3.2%。将模拟数据和实验数据进行对比,产生的误差在10%以内,说明了所建模型的准确性。此外,实验和模拟的结果都说明,在流体流速一定时,增加干度对于提高冷凝换热系数有十分明显的作用。

根据对换热器螺旋管所做的数值模拟以及实验研究可知,对数值模拟结果与实验结果进行对比,在不同流体流速时冷凝换热系数的模拟数据与实验数据之间的相对误差为3%～11%,在不同饱和温度时冷凝换热系数的模拟数据与实验数据之间的相对误差为3%～8%,误差工程计算的允许范围之内,说明数值模拟方法和结果是合理的。通过对流体流速和饱和温度模拟数据和实验数据进行对比,发现模拟数据均高于实验数据,产生误差的原因包括:在数值模拟中假设管道内壁为光滑的状态,但在实验当中管道内壁有一定的粗糙度,使工质的湍动能发生耗散,导致在实验过程中管内工质的实际速度低于设置的进口速度;模拟中假设温度是不发生变化的,而在实验过程中,温度是发生变化的,工质的热物性也会产生变化。