计及源/网不确定性的区域电网有功不平衡度评估
2023-12-14张瑞田佳李璐璐冯沛儒李坤李生虎
张瑞, 田佳, 李璐璐, 冯沛儒, 李坤, 李生虎*
(1.国网安徽省电力有限公司, 合肥 230000; 2.合肥工业大学电气与自动化工程学院, 合肥 230009;3.国网安徽省电力有限公司经济技术研究院, 合肥 230000)
随着化石能源枯竭和环境保护压力,新能源并网容量越来越大[1]。但是风电和光伏出力随机、波动,与负荷需求的匹配性较差,可能降低电网安全水平[2-3]。在新能源并网场景中,量化评估区域电网内电源与负荷间的有功平衡能力,可为电网运行和规划提供依据。
大型电网中,各区域电网通过联络线交换功率,从而在全网范围实现资源的优化配置,促进新能源消纳[4-5]。文献[6]提出了基于时序生产模拟的源网储一体化规划模型,证实电网互联可减少储能容量,降低运行成本。文献[7-8]研究发现,网架结构、电源配置、机组开机计划、负荷特性等因素均会影响风电消纳能力。通过优化联络线计划,合理安排调整区间交换功率,提高新能源利用率也是现有研究的一大热点。文献[9-10]考虑电网安全、交易合同实际执行等约束构建双层优化模型,将电网运行状态与联络线计划相结合制定省间的联络线计划。文献[11]首次建立跨区直流联络线的运行优化模型,从而充分利用直流联络线调整能力,但未考虑区域内部安全约束。文献[12]将不同时段的联络线载荷作为约束条件,提出分散式调度方法协调多区域发电资源。
但上述研究均是站在区域间角度,考虑电力电量平衡,全网统筹进行功率优化,较少关注单个区域内的源荷有功平衡问题。文献[13]研究了区间电力交换对区内风电、光伏承载能力的影响。区域间功率交换越多,联络线是否正常运行将成为关键。如果某电网过多依赖与其他电网电力交换,外网或联络线故障可能会大范围扩散导致电网安全不可控,因此需要评估区域电网有功不平衡度[14]。
鉴于此,计及风光出力不确定性和电网随机故障,提出区域电网有功不平衡度的评估指标和算法。改进聚类算法处理大量风光出力场景。定义两个区域不平衡度指标:电力不平衡度和供电能力不平衡度。考虑源/网不确定性,采用状态枚举和概率加权方法,计算区域电网不平衡度。改进发电再调度模型,将不平衡度指标分别纳入目标函数和约束条件;建立目标函数对约束的灵敏度模型,以量化调整不平衡度约束对优化目标的影响。通过算例结果验证所提算法的有效性,为区域电网安全运行具有指导意义。
1 风光出力场景聚类
为量化长时间尺度下电网不平衡度,引入聚类算法[15-17],以得到风光出力场景。负荷波动容易预测,且规划中多以最大负荷作为严重场景,因此未单独建模。传统聚类算法随机选取初始聚类中心,聚类结果不稳定且依赖于设定类数K。设共有S个场景,其中第i个场景si=(si,1,si,2,…,si,T)。计算场景间距离d(si,sj),计算公式见式(1),结果存入矩阵D见式(2)。
(1)
D[i,j]=d(si,sj)
(2)
式中:Si,a、Sj,a为场景i和j中的第a个数据;D[i,j]为矩阵D的第i行第j列。
对D每行从小到大排序,选取每行前m个距离较小值相加,作为每个场景密度。密度越小,与附近场景联系越紧密。选取密度最小场景se,作为第1个初始聚类中心c1。寻找第e行最大值,挑选与c1距离最远场景作为第2个初始聚类中心c2。
由最大最小距离准则确定其余初始中心。在D中寻找各场景si到c1、c2距离较小值,从中挑选最大者Li见式(3),对应场景为c3。重复上述步骤,确定K个聚类中心。按最小距离,将各场景分别分配到K类{C1,C2,…,CK}。计算各类平均值作为新的聚类中心,重复计算直至聚类中心不再改变。
Li=max{min[d(si,c1),d(si,c2)]}
(3)
采用DBI(Davies Bouldin index)如式(4)、式(5)[18]所示,以及SC(silhouette coefficient),如式(6)[19]所示来判断类间分离性、类内紧密性。DBI越小聚类效果越好;SC越接近1越好。由此确定最优K。具体步骤如图1所示。
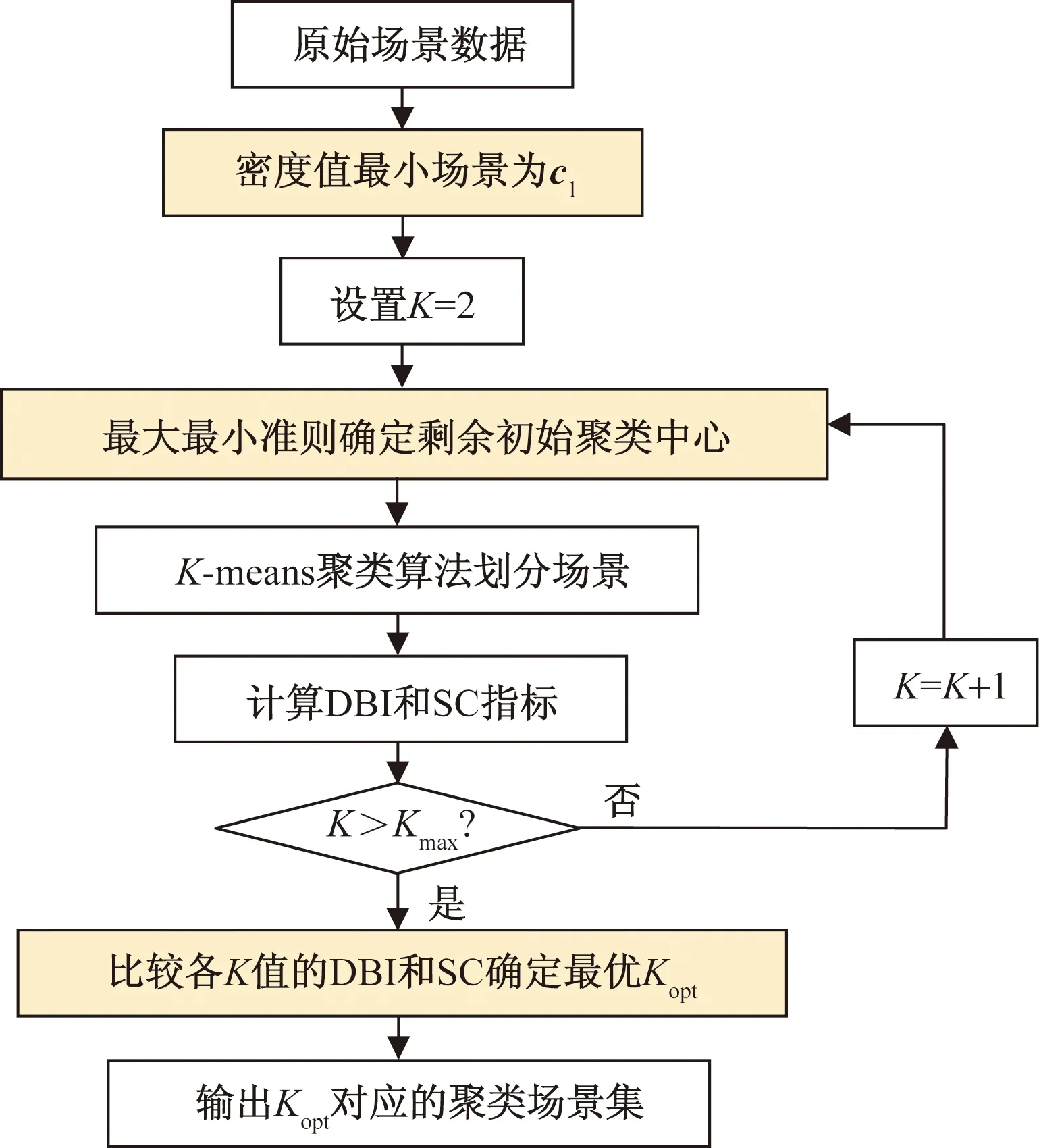
Kmax为设置的最大类别数;Kopt为最佳分类数
(4)
(5)
(6)
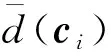
2 区域电网不平衡度指标和算法流程
所提区域电网有功综合不平衡度指标由电力不平衡度γ1和供电能力不平衡度γ2构成,分别从源荷匹配程度和供电阻塞两方面来衡量区域电网的有功平衡能力。
γ1为区域内机组出力和负荷比值与1的差值的绝对值[式(7)],反映区域内源荷不匹配的程度。
(7)
式(7)中:I为区域编号;PGi、PWi、PVi、PLi分别为节点i的常规机组、风电、光伏、负荷有功。
在电网故障后,经调度仍可能切负荷。将区域内可增发有功与切负荷差的绝对值,定义为γ2[式(8)],反映电网安全约束对区域供电阻塞的影响。
(8)
式(8)中:ΔPGi为常规机组有功发电裕度;ΔPLi为切负荷量。
兼顾电力不平衡度和供电能力不平衡度,定义区域电网I处于某运行状态下的综合不平衡度φI,可表示为
φI=ω1γ1,I+ω2γ2,I
(9)
式(9)中:ω1、ω2分别为相应权重。
图2给出区域电网不平衡度算法流程。基于风电、光伏数据聚类,计算DBI、SC以判断最佳类数。对每一场景,枚举发电机和线路故障,根据设备可用率计算全网状态J概率pJ[20]。通过潮流计算,判断是否有过载、常规机组出力或节点电压越限。若有,将不平衡度引入目标函数和约束条件,对全网发电再调度。枚举全网全部状态(总数W),概率加权得到区域I的综合不平衡度φI,ALL,可表示为
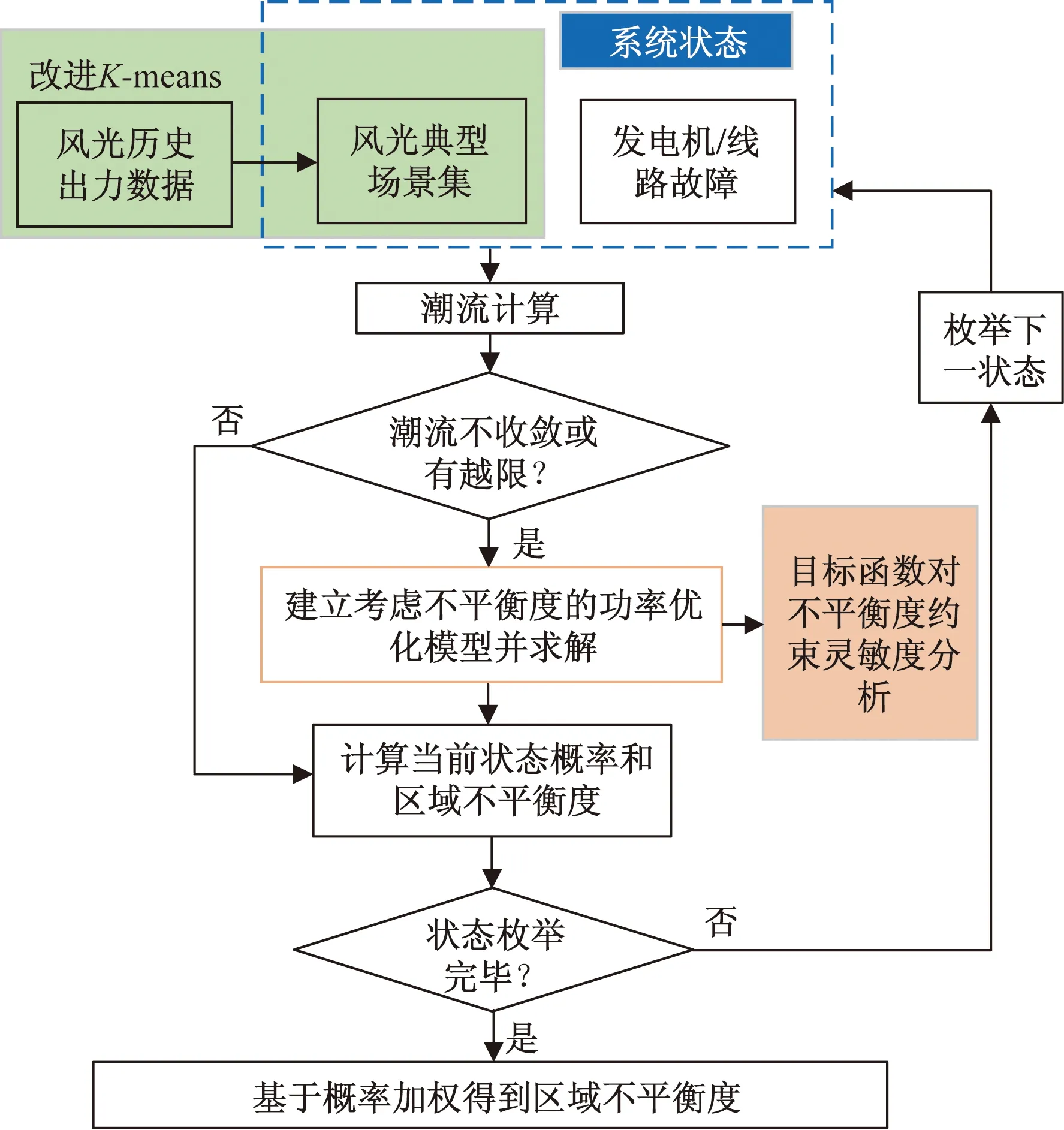
图2 区域电网不平衡度评估流程图Fig.2 Flow chart for assessing the imbalance degree of regional grids
(10)
式(10)中:φI,J为区域电网I在运行状态为J时的综合不平衡度。
3 考虑不平衡度的发电再调度模型
3.1 目标函数和约束条件
当违背电网安全约束时,若用传统的切负荷模型优化调度,可能需通过相邻区域增加输出减少切负荷,此时单个区域的电力不平衡度会增加,联络线功率传输压力增大,成为是否会引发进一步故障的关键。 因此改进调度模型,将故障影响控制在本区域内。
现有优化模型通常不直接以发电裕度为目标,常用与其相关的发电成本来表示。因此,将γ2分为两项:发电成本f1和最短距离加权的切负荷f2;取γ1为f3,建立目标函数f,可表示为
(11)
(12)
(13)
f=min(ρ1β1f1+ρ2β2f2+ρ3β3f3)
(14)
式中:ND为全网节点数;R为区域电网数;NG为常规机组数;a1i、a2i、a3i为燃料费用系数;εPi为节点离故障点最短距离;ρ1、ρ2、ρ3为对应于发电成本、切负荷量、γ1的权系数;为了协调f1、f2、f3数值大小,引入系数β1、β2、β3。
约束条件包括节点功率平衡式(15)、式(16)、常规机组出力约束[式(17)]、电压约束[式(18)]、载荷约束[式(19)]、切负荷量约束[式(20)]。新增γ1约束[式(21)],以便降低区域电网电力不平衡度。
PGi+PWi+PVi-PLi+ΔPLi-
观察组在使用甲钴胺治疗的基础上(具体剂量与方法对对照组患者一致),增加使用前列地尔(国药准字H10980024)进行治疗,具体剂量及方法为,10 μg 的前列地尔配以0.9%氯化钠注射液100 mL ivdrip qd。2组患者均进行为期4周的治疗。
(15)
(16)
(17)
Vi,min≤Vi≤Vi,max
(18)
(19)
0≤ΔPLi≤PLi
(20)
0<γ1,I<γ1,I,max
(21)
式中:Vi、Vj分别为节点i、j电压幅值;Gij、Bij分别为线路ij电导和电纳;θij为相角差;QGi、QLi、ΔQLi分别为常规机组、负荷、切负荷无功;Pij、Qij分别为线路ij有功和无功;Sij,max为线路载荷上限;PGi,max、PGi,min、QGi,max、QGi,min分别为发电机有功、无功出力上下限;Vj,max、Vi,min为电压幅值上下限;γ1,I,max为区域I的电力不平衡度上限。
3.2 目标函数对约束灵敏度
为量化不平衡度约束对目标函数的影响程度,根据目标函数对γ1上下限求导建立灵敏度模型。γ1下限为0,因此对其上限求灵敏度。构造拉格朗日函数为
F=f(x)-yTh(x)-zT[g(x)-l-gmin]-
wT[g(x)+v-gmax]-
(22)
式(22)中:x为变量;f(x)为目标函数;h(x)为等式约束;g(x)为不等式约束;gmax、gmin分别为不等式约束上下限;rr为不等式约束个数;lq、vq为第q个松弛变量,对应矩阵为l、v;y、z、w为拉格朗日乘子;μ为扰动因子。
式(22)存在极值的条件是,其变量偏导为0,即最优解xopt满足式(23)。
∂F/∂x=∇xf(xopt)-∇xh(xopt)y-
∇xg(xopt)(z+w)=0
(23)
式(23)中:∇x为目标函数对x的梯度。
式(23)两端同乘以dx得式(24)。
(24)
式(24)中:mm为等式约束数;yq、zq、wq为对应的第q个拉格朗日乘子;hq、gq分别为第q个等式和不等式约束。
将gq用γ1约束替换求得灵敏度[式(25)],为对应的拉格朗日乘子ωγ,1,I,其物理意义为当γ1约束上限调整量为dγ1时,引起目标函数[式(14)]的变化量。
(25)
4 算例分析
全网由两个区域电网(IEEE-RTS和IEEE-14系统)组成,通过2条联络线交换功率(图3),其中区域A负荷更密集。共有常规机组16台,输电支路56条。节点6接入光伏,节点18接入风电。基准容量为100 MW。发电机、线路参数来自文献[21-22]。
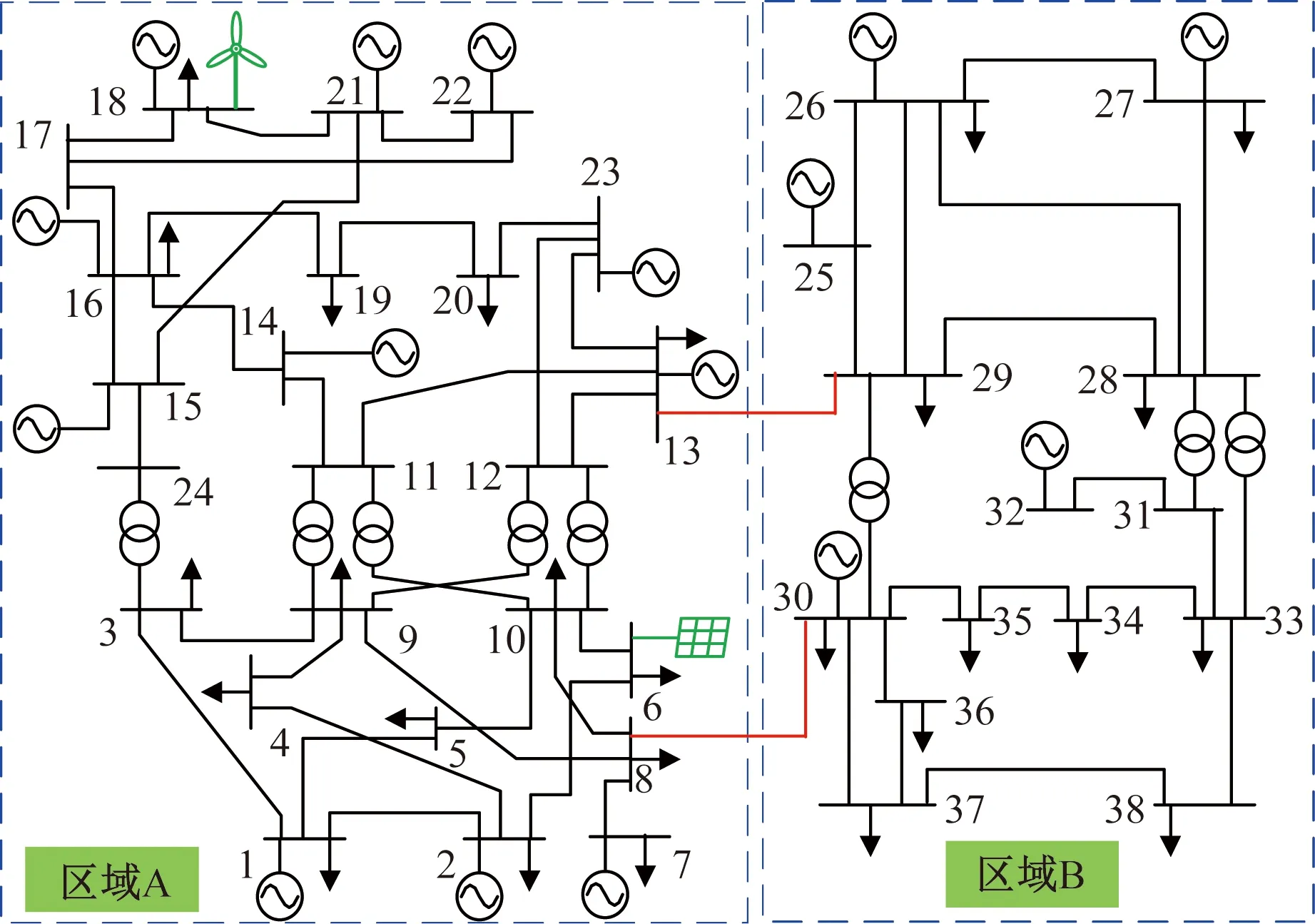
图3 多区域电网结构Fig.3 Structure of multi-region grid
4.1 风光场景聚类结果
以一个月风电/光伏历史数据为样本,采用改进聚类算法,计算有效性指标如表1所示。当风电K=4、光伏K=3时,DBI最小,SC最接近于1,效果最好,如表1中加粗数据所示。因此将风电聚为4类,光伏聚为3类。将聚类结果组合为出力场景,如表2所示。
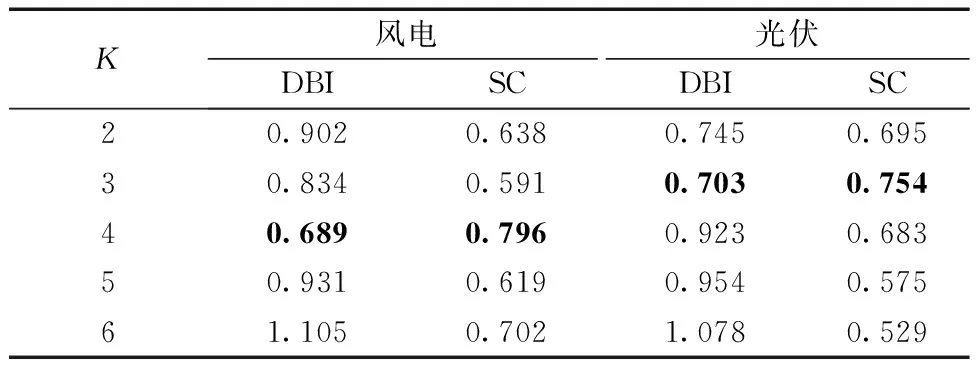
表1 不同K值下DBI和SC Table 1 DBI and SC with different K
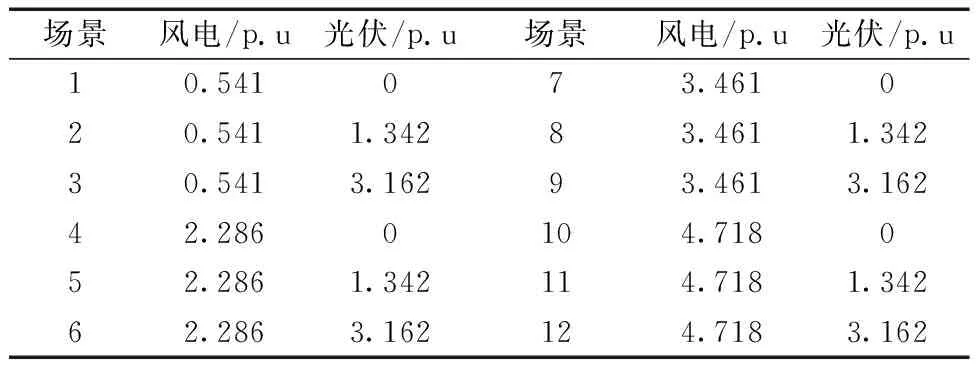
表2 聚类场景组合情况Table 2 Combination of clustering scenarios
4.2 不平衡度评估结果
目标函数中切负荷重要程度大于发电成本和γ1,因此ρ1、ρ2、ρ3分别取0.2、0.6、0.2;统一为成本的数量级,β1、β2、β3分别取1、104、104;约束γ1,I,max设置为0.2;综合不平衡度根据γ1、γ2波动范围,ω1、ω2分别取0.8、0.2。场景6中,枚举线路8~10停运,经潮流计算,节点2、13无功越限,线路6~10过载。采用考虑不平衡度的发电再调度模型后,各节点有功如图4所示。

图4 经优化后各节点有功Fig.4 Active power of each node after optimization
将所提优化模型作为模型1,将其与以切负荷f2为目标函数的模型2对比,结果如表3所示。模型2比1切负荷量减少0.210 3p.u,但不平衡度γ1,B超过了γ1,B,max范围。模型2调度是通过区域B增加发电或切负荷弥补区域A故障影响,牺牲了相邻区域利益,增加了联络线压力。模型1以切负荷量增多为代价,使γ1控制在允许范围内,同时两区域γ2分布相对均匀,使得区域A综合不平衡度降低0.483,区域B降低0.294 3,减小了联络线压力。
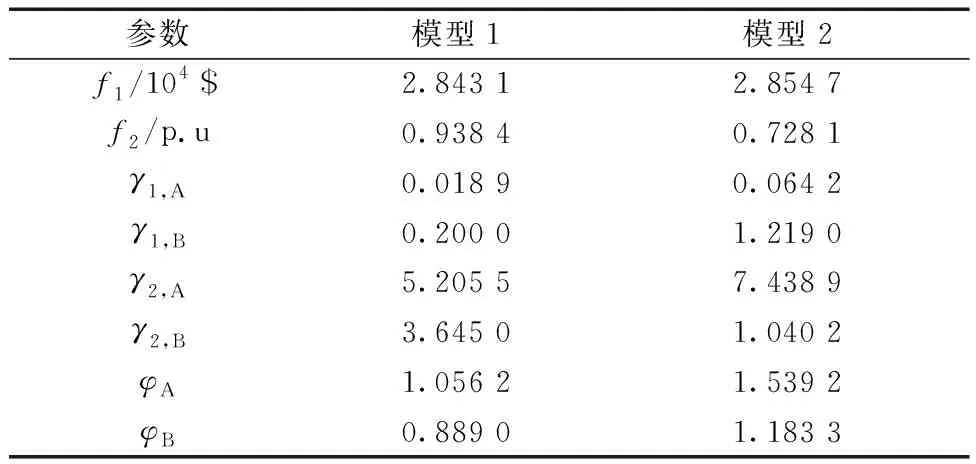
表3 两种优化模型结果对比Table 3 Comparison of the results with 2 optimization models
在每一场景下枚举电网故障,概率加权计算各区域综合不平衡度如图5所示。A区域综合不平衡度φA,ALL和B区域综合不平衡度φB,ALL曲线变化趋势基本一致,因为发电再调度是站在全网电力电量平衡的角度,各区域功率变化趋势基本一致。φA,ALL平均值大于φB,ALL平均值,区域A综合不平衡度更高。
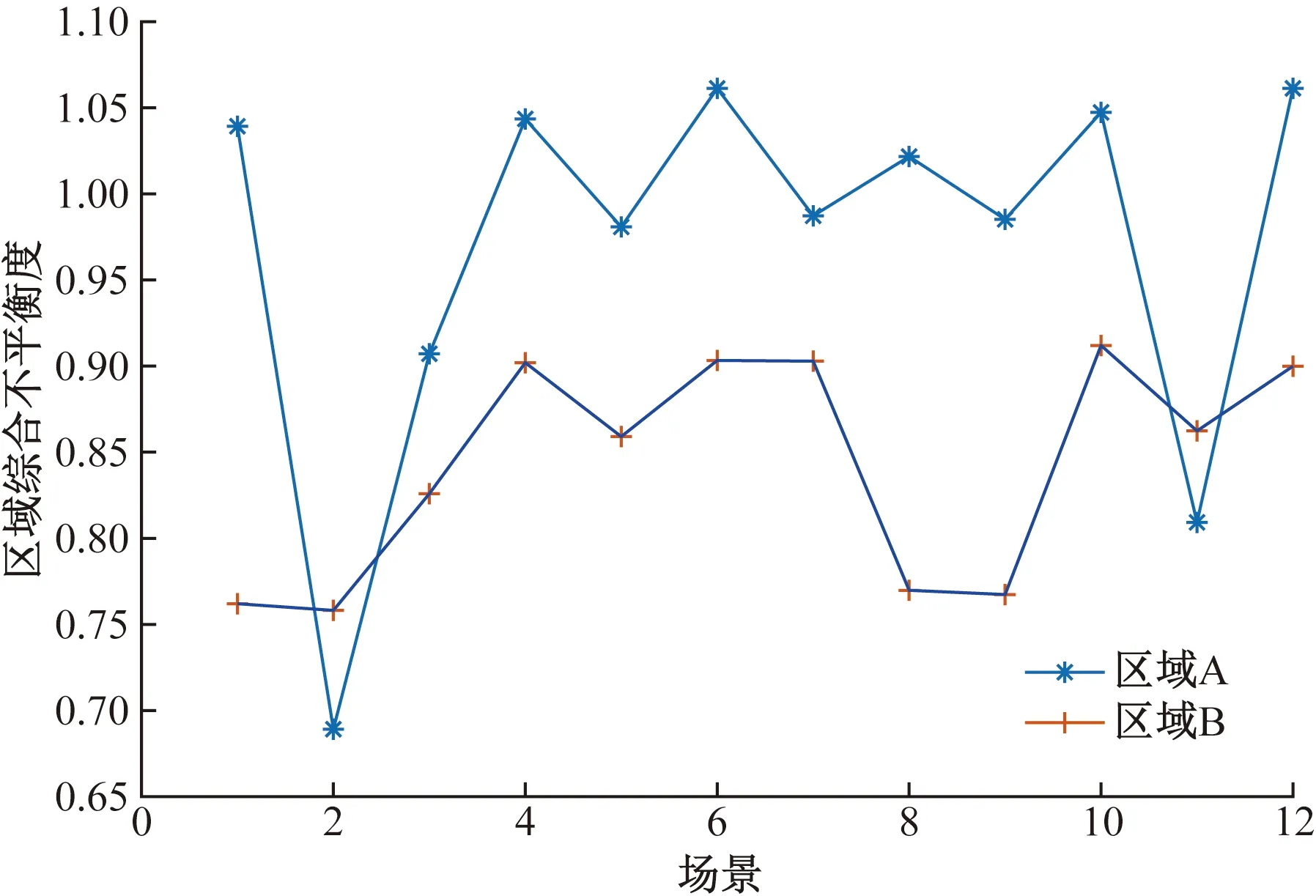
图5 区域电网的综合不平衡度Fig.5 Comprehensive imbalance of regional grids
对场景12,枚举发电机/线路故障,比较ρ1、ρ2、ρ3取值不同时指标如表4所示。随γ1权系数ρ3增加,区域综合不平衡度φA,ALL和φB,ALL均下降。当ρ1由0.4下降为0.3,ρ3由0.1增加到0.2时,发电成本增加270$,切负荷量增加0.006 p.u。目标函数中γ1加权系数ρ3增加,使得综合不平衡度降低,但以切负荷量和成本增长为代价,因此ρ3取值不宜过大。
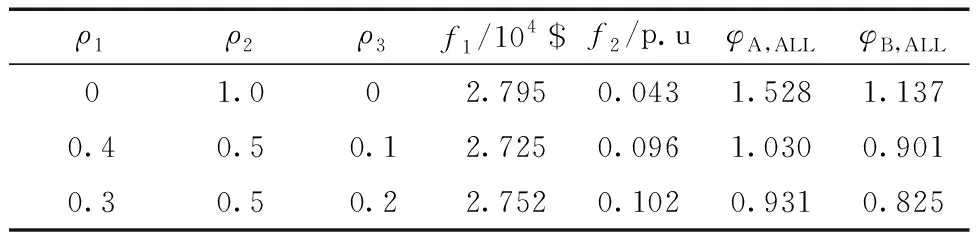
表4 ρ不同时优化结果Table 4 Optimization results with different ρ
4.3 目标函数对约束灵敏度
计算与γ1,I,max对应拉格朗日乘子w,得到目标函数对γ1,I,max灵敏度,以量化不平衡度范围的影响。枚举864个状态,统计∂f/∂ϒ1,I,max概率分布如图6所示。∂f/∂γ1,I,max为正,说明增加γ1上限将扩大最优解范围,目标函数减小;∂f/∂γ1,I,max越小,说明最优解越远离γ1,I,max边界;反之越靠近γ1,I,max边界。以表3场景为例,γ1,B为0.2,到达边界,此时∂f/∂γ1,B,max=1.493 7,表示若γ1,B,max变化1%,f将减小0.000 127%。
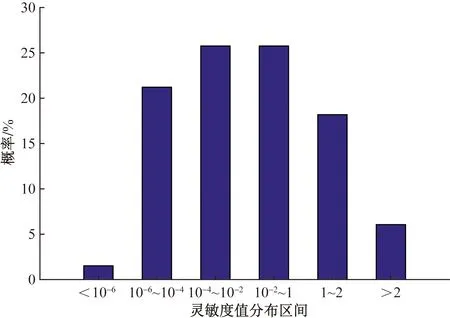
图6 ∂f/∂γ1,I,max概率分布Fig.6 Probability distribution of ∂f/∂γ1,I,max
计算∂f/∂γ1,I,max与∂f/∂PGi,max如表5所示,其中出力接近上限的发电机组灵敏度大于∂f/∂γ1,I,max,这些机组出力上限取值对优化目标改善效果强于γ1,I,max。其中,∂f/∂PG16,max最大且为正,对于相同的优化目标降低量,PG16,max的增加量最小,代价最低。因此,这些灵敏度值量化不等式约束范围对目标函数的改善效果,从而以最小调整代价达到最好改善效果。
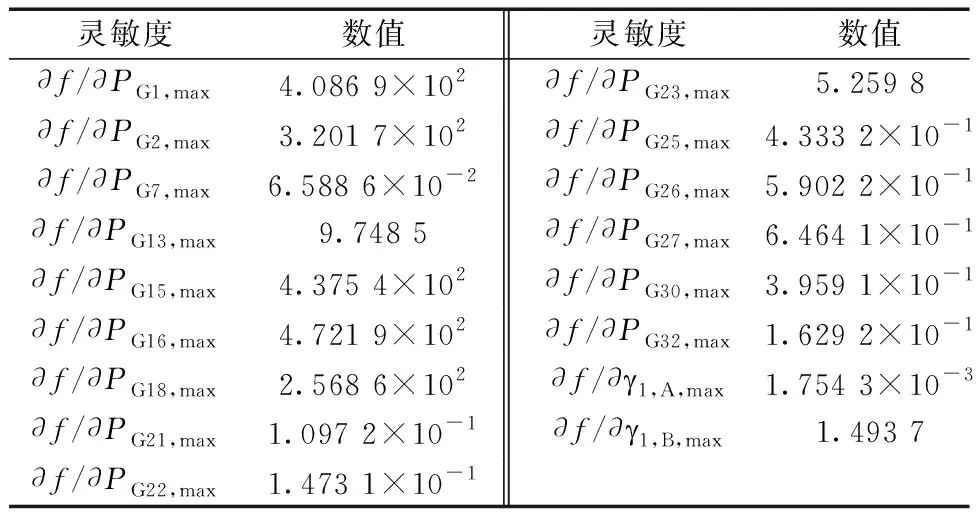
表5 ∂f/∂γ1,I,max与∂f/∂PGi,max计算结果Table 5 Calculation results of ∂f/∂γ1,I,max and ∂f/∂PGi,max
5 结论
新定义区域电网不平衡度指标,计及新能源出力不确定性及电网随机故障,提出不平衡度评估方法和优化模型,得到以下结论。
(1)与传统切负荷模型相比,所提发电再调度模型可以降低区域电网有功不平衡度。
(2)各区域在不同风光出力、电网故障状态下综合不平衡度指标变化趋势基本一致。目标函数γ1权重增加,综合不平衡度指标下降。
(3)灵敏度可以量化调整约束范围对优化目标的影响。选择灵敏度值大的约束条件,能以较小的调整量改善综合目标函数。
