基于改进麻雀搜索算法的路径规划*
2023-12-13司马燊刘汉明刘财辉胡鹏程
司马燊,刘汉明,†,刘财辉,郭 港,余 聪,胡鹏程
(1.赣南师范大学 数学与计算机科学学院;2.江西省数值模拟与仿真技术重点实验室,江西 赣州 341000)
0 引言
路径规划[1]算法可分为两大类,一种是以A*、快速搜索随机树[2-4]等为主的启发式算法,另一种是以蚁群算法(Ant colony optimization,ACO)[5]、遗传算法(Genetic Algorithms,GA)[6]、模拟退火算法(Simulated Annealing,SA)[6]、麻雀搜索算法(Sparrow search algorithm,SSA)[7]等为代表的群智能算法.其中,启发式算法存在搜索时间长、全局遍历开销大、计算效率低等问题.群智能算法由于寻优能力强、实现容易等优点被广泛使用,如工业优化[8]、路径规划[9-15]、优化计算[16]等领域,这些领域中也经常看到麻雀算法[17]的身影.在群智能路径规划领域,MIAO[12]等提出基于自适应蚁群算法的室内移动机器人路径规划算法,采用自适应启发因子和信息素挥发因子来平衡全局搜索和算法的收敛能力.MACTT[18]等人提出分层的路径规划方法,平衡路径的平滑度和最短路径.以上文献虽然取得了不错的效果,但是搜寻实验地图中的障碍物分布较为集中,并没有真正平衡算法全局和局部搜索.
受上述文献的启发,本文提出基于适应度值变化的自适应麻雀搜索算法(Adaptive sparrow search algorithm,ASSA)的移动机器人(Automated guided vehicle, AGV)路径规划.
1 麻雀搜索算法基本原理
SSA把麻雀分为发现者、追随者和预警者三种角色进行寻优.每只麻雀代表当前问题的可行解,麻雀的位置可表示为

(1)
其中n表示群体中麻雀的数量,d是要优化的变量的维度.麻雀和食物之间的匹配程度用适应度衡量,其适应度值为

(2)
发现者第t+1轮迭代时的位置:
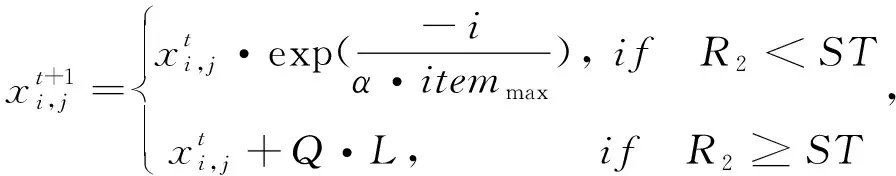
(3)
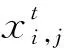
一旦发现者找到更好的食物,他们就会立即前往相应的位置进行竞争.追随者第t+1轮迭代时的位置
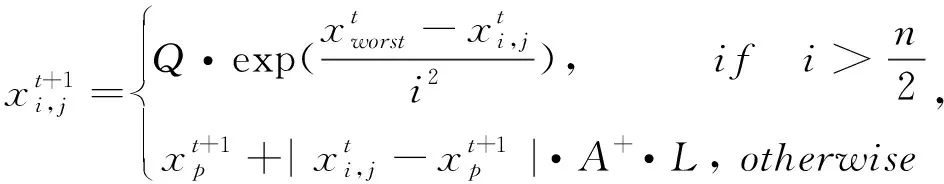
(4)
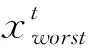
另外,麻雀群体中的预警者对天敌作出预警,使得发现者带领群体飞向更安全的地方.预警者t+1轮迭代时的位置
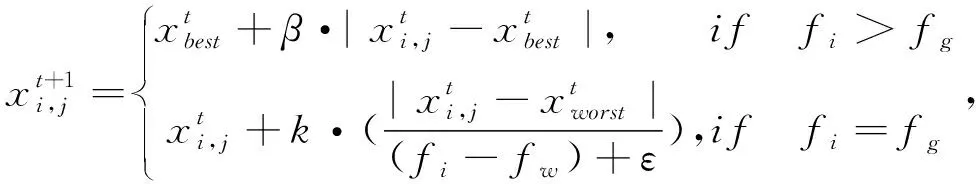
(5)

2 改进的麻雀搜索算法
2.1 发现者更新策略
由式(3)知,R2和ST的取值决定其是把群体带到安全区域还是在原有区域继续搜索,即全局搜索或局部搜索.现有研究大多集中在更新策略[19-22],在ST的取值上研究不多.结合本文研究的具体实例,将适应度值变化与ST的更新进行关联,即在迭代过程中最优适应度值发生变化时(麻雀找到了更好的食物),将ST的取值扩大,促使发现者在当前迭代中偏向于局部搜索,加速种群的收敛速度,反之则偏向于全局搜索,进一步扩大搜索范围.具体更新策略为

(6)
2.2 追随者更新策略
SSA追随者以固定的n/2为更新策略边界,限制了算法的适应性,同时A+的复杂运算拖慢了算法的运算速度.这里将式(4)的更新策略边界改为B,随迭代数变化而变化
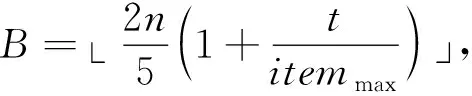
(7)
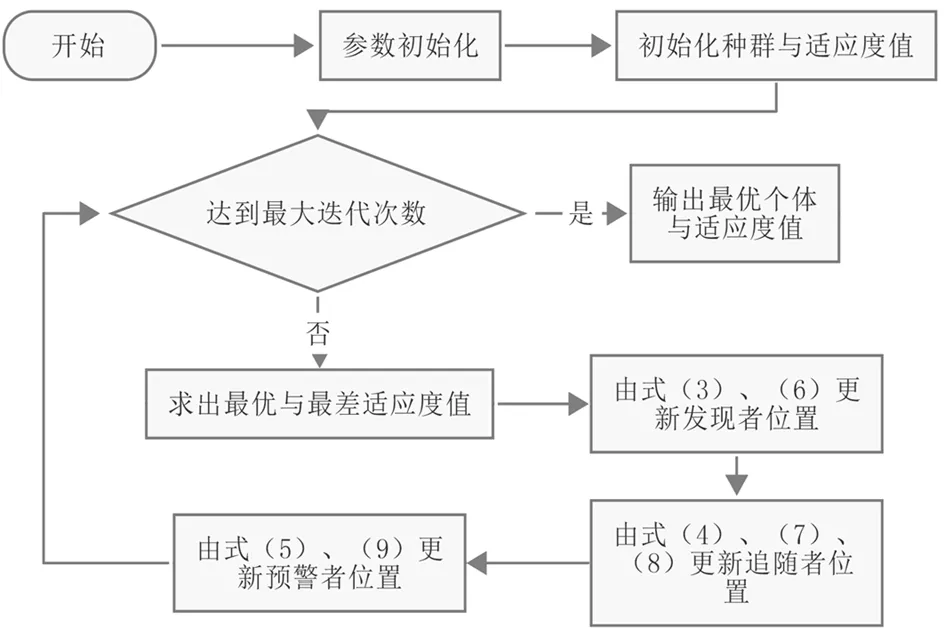
图1 改进后的算法流程
2.3 随机保留策略
SSA的更新策略在迭代前期效果较好,但中后期,麻雀均聚集在最优解附近,使种群趋同性严重,增加了陷入局部最优的风险.本文以一定概率随机地保留意识到危险的麻雀和劣于上一轮迭代的追随者的位置不变,有助于提高种群多样性,降低陷入局部最优的风险.随机保留策略为
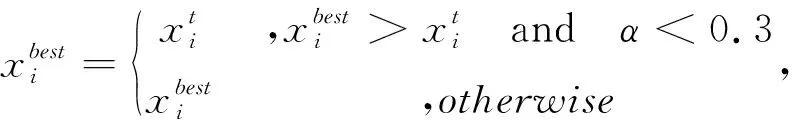
(9)
2.4 改进后的算法流程(图1)
3 实验结果与分析
为验证算法改进在理论上可行,除节3.4算法应用实验外,其它实验所使用的测试集为基准公开测试集[23]中的11个(表1).实验环境为Windows11 64位、内存16GB、Intel Core i7-10870H.

表1 基准测试函数
3.1 ξ参数优化
取ξ为0.1-0.9(步长0.1)的ASSA实验结果如表2、表3所示,其中Best和Mean分别表示获得最好的最优值、均值的数量.

表2 常数ξ优化实验结果*
*较好的结果加粗倾斜表示,表4同.

表3 常数ξ优化实验结果统计*
*各算法在11个测试函数中取得最好的最优值和均值的函数数量.
由表2、表3可知,参数ξ为0.4左右时效果较优.
3.2 性能比较
为验证ASSA的性能,把其与麻雀算法(Sparrow search algorithm,SSA)、粒子群算法(Particle swarm optimization,PSO)、灰狼算法(Grey wolf optimization,GWO)、正余弦算法(Sine cosine algorithm,SCA)、树种优化算法(Tree seed algorithm,TSA)和风驱动算法(Wind driven optimization,WDO) 进行对比实验.PSO参数的c1=2,c2=2,ω=2,SCA的a=2,TSA的st=0.1,WDO的rt=0.3,g=0.2,alp=0.4,ω=0.3,GWO的αinitial=2,αend=0,SSA的PD=0.2,SD=0.2.所有算法的种群规模为50、最大迭代次数为100,进行30次独立实验,取各算法求解的最优值(Best)、最差值(Worst)、均值(Mean)及标准差(Std),实验结果示于表4,同时表5给出了各算法平均性能优于其他算法的数量.
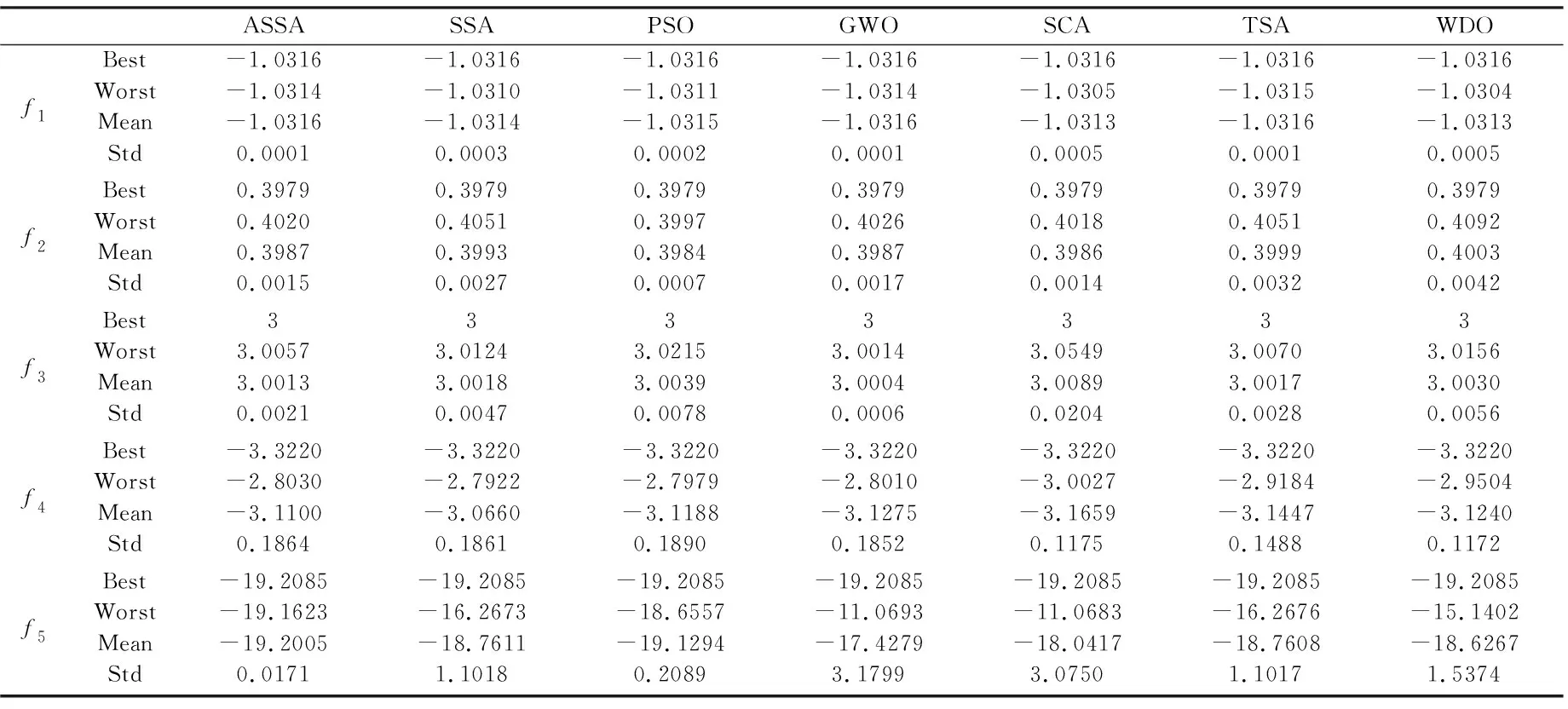
表4 对比实验结果
表4显示,虽然SSA与ASSA一样都能在实验中取得相同的最优值(Best),但在算法的平均性能(Mean)上SSA均劣于ASSA.另外,表5显示ASSA的平均性能在所有测试算法中最优.
3.3 收敛速度比较
为直观对比各算法收敛速度,绘制30次实验中各轮迭代适应度值均值的变化曲线(图2-12),为了更好地显示与SSA的差异,单独绘制ASSA与SSA对比.

图2 F1平均适应度曲线 图3 F2平均适应度曲线

图4 F3平均适应度曲线 图5 F4平均适应度曲线

图6 F5平均适应度曲线 图7 F6平均适应度曲线
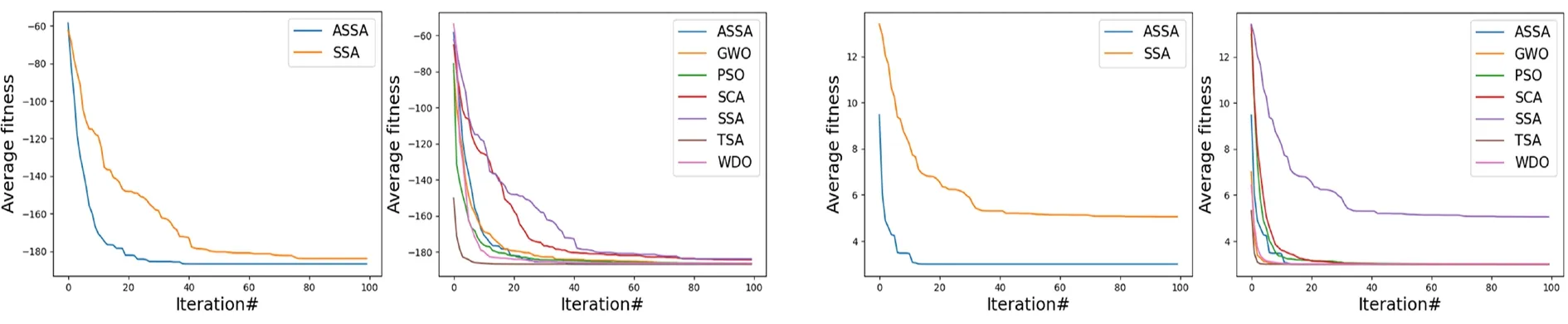
图8 F7平均适应度曲线 图9 F8平均适应度曲线
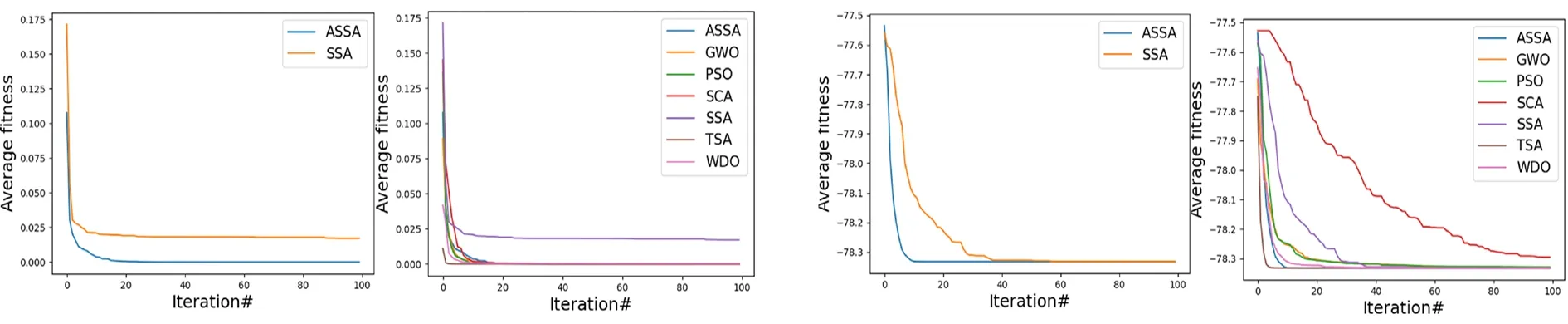
图10 F9平均适应度曲线 图11 F10平均适应度曲线
根据图2-12函数平均适应度值收敛曲线知,
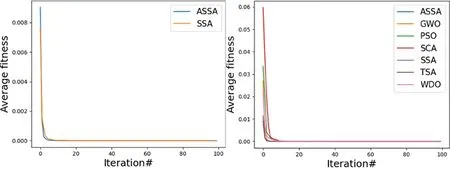
图12 F11平均适应度曲线
不论是在单峰还是多峰函数,改进后的ASSA算法在不降低寻优能力的前提下获得了更快的收敛速度,收敛到同等精度所需的迭代次数更少,尤其在迭代前期收敛速度增加更为明显,说明对麻雀算法在发现者和追随者的策略选择阈值上改进有效,随着算法迭代到后期,ASSA和SSA收敛趋势基本趋同,说明随机舍弃策略并未对算法收敛产生较明显的负面影响.
3.4 移动机器人路径规划
为验证ASSA在移动机器人路径规划上的效果,将其与原算法SSA应用于栅格地图下进行路径规划,实验环境与理论验证相同,栅格地图为随机生成.
3.4.1 任务环境建模
在进行机器人路径规划前选用栅格地图法[24]建模.这里用矩形栅格表示地图,地图中有随机分布的障碍物(蓝色栅格)、可行区域(白色栅格),并包含起点(绿色栅格)和终点(红色栅格).除起点和终点外,地图中每一个栅格存在关系
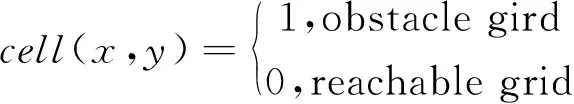
(10)
3.4.2 代价函数
路径规划常将路径长度作为其优劣程度的评价指标,故本文路径长度的代价函数为
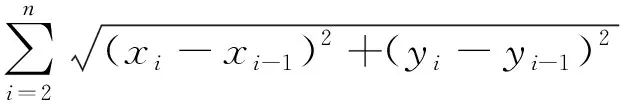
(11)
n表示生成路径中栅格的个数.
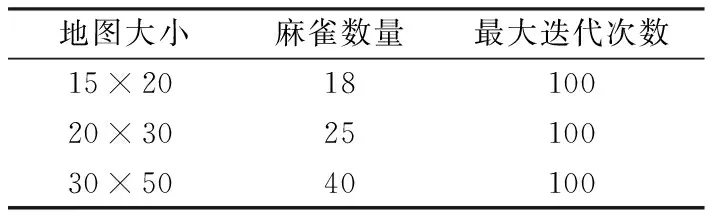
表6 路径规划参数
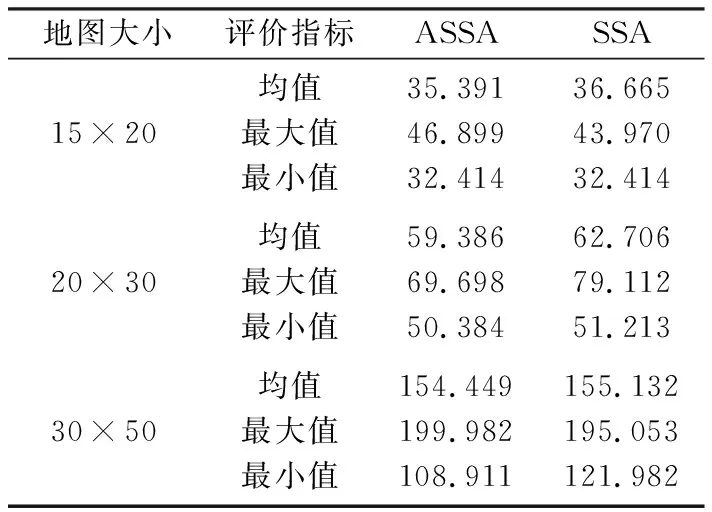
表7 路径规划结果
3.4.3 实验参数说明
栅格地图大小、麻雀数量、最大迭代次数等参数如表6所示,均进行30次独立实验,实验要求在每一列选择一个可行栅格直至终点.
3.4.4 实验结果与分析
实验结果如表7及图13-18所示.
根据表7中的实验结果知,在三类大小地图中ASSA规划出来的平均路径长度均小于SSA,证明在路径长度上ASSA整体性能优于SSA.,结合图13-18的两类算法规划的路径图,ASSA规划出的路径比SSA更平滑.但实验表明,随着地图的增大、障碍物分布的复杂程度上升,不论是ASSA还是SSA都无法凭借自身单一的算法找到最优路径.故此,在后续的研究上除算法改进外还需考虑栅格地图处理.

图13 15×20地图的ASSA最优路径 图14 15×20地图的SSA算法最优路径 图15 20×30地图的ASSA算法最优路径
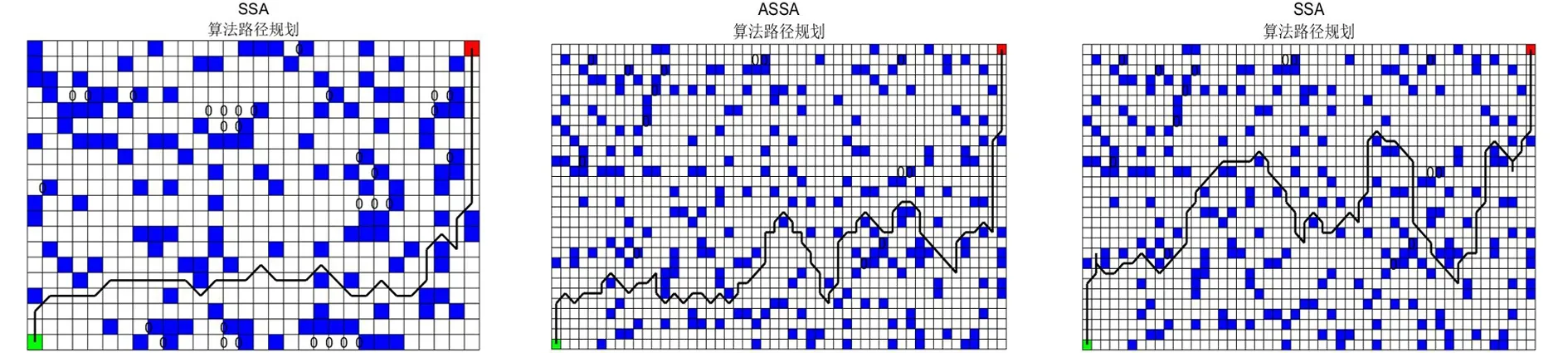
图16 20×30地图的SSA算法最优路径 图17 30×50地图的ASSA算法最优路径 图18 30×50地图的ASSA算法最优路径
4 结论
对于SSA算法存在的易陷入局部最优等问题,本文提出了改进的算法ASSA.该算法通过动态调整发现者的预警值、追随者的边界值及随机保留追随者和预警者非最优位置等策略提高了算法的全局寻优能力,降低了算法陷入局部最优的概率,提升了算法整体的寻优效率和精度.与6个常用算法在11个基准测试函数的比较实验结果表明,相比于SSA,ASSA具有更好的性能和更快的收敛速度及更强的鲁棒性,综合性能上有较大的提升,并在路径规划中取得了较好的结果.但大规模地图、障碍物分布复杂的情况下, ASSA与SSA一样,无法获得最优路径,有待于后续的进一步研究.
