利用加权对数范数分解的矩阵填充算法*
2023-12-13赖烨辉黄慧英彭绍婷胡文玉
赖烨辉,黄慧英,彭绍婷,胡文玉
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
0 引言
低秩矩阵填充问题是指基于矩阵的低秩特性,利用已知的部分元素合理精确地将未知元素进行填充.具体来说,给定不完整数据的观察矩阵Y∈m1×m2,矩阵填充问题可转化为求解如下优化问题[1]:
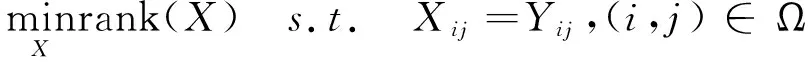
(1)
其中X∈m1×m2是待恢复的准确数据,Ω表示与观测数据元素对应的位置集合.
然而,由于秩函数的非凸性和不连续性,上述秩极小化问题是NP-难问题.因此,秩函数通常被核范数替代.然而,作为一种凸的近似替代函数,核范数极小化结果通常会偏离实际秩极小化的结果,这是因为核范数无差别地将X的所有非零奇异值相加,造成矩阵的大奇异值被过度惩罚,而在实际秩极小化问题中,所有非零奇异值都受到等量对待.为了克服上述问题,研究人员选择用非凸替代函数来近似秩函数,从而获到了更好的实验结果.例如,Gu等[2]提出了基于加权核范数的极小化问题(Weighted Nuclear Norm Minimization, WNNM),其利用加权核范数代替核范数作为模型的低秩惩罚项,降低了对大奇异值的惩罚度;Chen等[3]提出使用对数范数代替核范数作为模型的低秩惩罚项,进一步降低对大奇异值的惩罚度.
上面提出的方法都需要计算完整的奇异值分解(Singular Value Decomposition, SVD).在处理大规模数据时,SVD需要大量的计算成本和时间,这限制了它们在处理大规模问题时的适用性[4].为了解决这个问题,研究人员提出了基于低秩分解的矩阵填充方法.例如Cabral等[4]提出了一种核范数的双线性分解方法,他们证明:任何矩阵都可以分解为两个因子矩阵的乘积,并且矩阵的核范数等于两个因子矩阵的Frobenius范数(F范数)平方之和的一半.Lin等[5]推广至一种更一般的鲁棒矩阵分解方法(Robust Matrix Factorization, RMF).然而,这些只是核范数的双线性分解,结果仍然偏离实际的秩极小化结果.为此,Chen等[6]结合重加权核范数极小化和双线性分解,提出了重加权低秩矩阵分解(Reweighted Low-Rank Factorization, RLMF).此外,Chen等[3]提出了一种对数范数矩阵分解(Logarithmic norm Regularized Matrix Factorization, LRMF).以上方法虽然一定程度上能够抑制大奇异值的过度惩罚问题,但是在低秩分解上由于缺少可调控参数,灵活度不够.
为此,本文提出一种利用加权对数范数矩阵分解(Weighted Logarithmic norm Matrix Factorization,WLMF)的矩阵填充算法,其中使用加权对数范数作为秩函数的非凸替代函数,通过引入权重参数和指数参数,能更灵活的进行矩阵分解并进一步地抑制大奇异值的过度惩罚.
1 相关工作
给定一个不完整的观测矩阵Y∈m1×m2,矩阵Y的部分元素缺失,其他可观测的元素可能被噪声污染.设W∈m1×m2为一个0-1指示矩阵,元素1和0取值分别映射被观察到和缺失元素的位置[4].考虑到噪声的存在,矩阵填充问题的一般模型为:
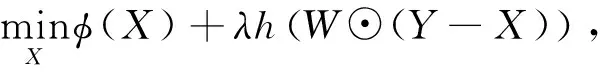
(2)
其中⊙表示Hadamard积,第一项φ(·)是与X秩函数相关的低秩正则化项,第二项h(·)是消除噪声的数据拟合项,λ>0为惩罚参数.针对不同的噪声类型,可以使用不同的拟合项.例如,稀疏噪声常用1范数刻画,高斯噪声常用F范数刻画.由于直接极小化矩阵秩函数是NP-难的,低秩正则化项通常使用凸的核范数来替代,即其中σi(X)表示X的第i大奇异值,其顺序按大小递减排列.为了抑制大奇异值的过度惩罚,Gu等[2]提出加权核范数作为秩函数的非凸替代函数,即
但是,使用式(2)中的极小化框架,矩阵填充需要执行完整的SVD.为了解决这个问题,研究人员设计了一个具有可分离的低秩正则化双因子框架来代替式(2):

(3)
其中U∈m1×r和V∈m2×r是因子矩阵,满足r≪min{m1,m2}.式(3)在优化求解过程中只需要在两个因子矩阵上计算SVD,不需要像式(2)优化时需要计算大规模矩阵的SVD,从而显著降低计算成本和时间.在此框架内,Cabral等[4]提出了矩阵核范数的双因子等价替代,等式如下:
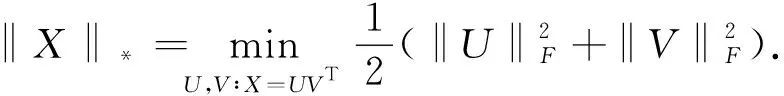
(4)
但这种方法没有避免核范数极小化结果偏离真实秩极小化结果的问题.为此,Chen等[6]提出了重加权核范数的双因子等价替代,等式如下:

(5)
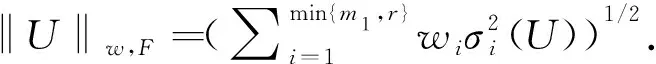

(6)
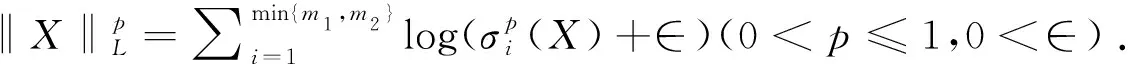
2 利用加权对数范数因子分解的矩阵填充
首先介绍加权对数范数因子分解的相关定义与理论性质,然后给出基于加权对数范数因子分解的矩阵填充模型和求解算法.
2.1 加权对数范数因子分解
在秩极小化问题中,研究人员使用秩的非凸替代函数代替秩函数.基于此,本文提出如下的加权对数范数作为秩的非凸替代函数.对于任意矩阵X∈m1×m2,定义

(7)
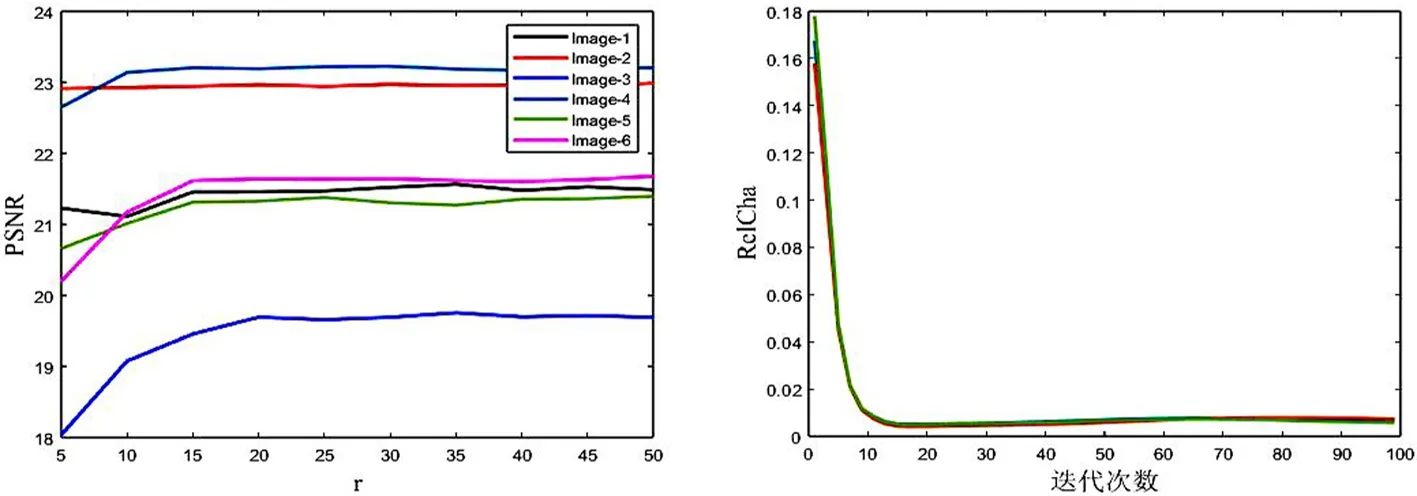
其中σi(X)表示X的第i个奇异值,0 图1 秩函数与不同秩代替函数的对比图σ表示奇异值,f(σ)表示函数值 严格来说,加权对数范数只是一种伪范数,因其不满足范数的三角不等式.从图1可以看出与其他秩替代函数相比,它可以更大程度上抑制大的奇异值惩罚度,惩罚的程度可以通过调整参数p来灵活控制.同时,权重w的引入,不仅可以进一步降低大奇异值的惩罚程度,还可以降低小奇异值的惩罚程度.其中小的奇异值通常被认为是噪声,这使得模型更加具有鲁棒性.虽然加权对数范数整体的函数值小于秩函数,但是不同大小的奇异值的惩罚度更加相近. 类似于式(4)中核范数与双因子矩阵F范数的等价关系,本文提出加权对数范数的双因子等价替代,结果见如下定理1.与Chen等提出的结果(式(6))相比,其矩阵分解只能在p=1/2时进行,而本文提出的双因子分解具有更高的调控灵活性,p可取(0,1]范围内的任意值时进行分解.同时,权重w的引入也增强了本文提出模型的可扩展性. 引理2设f(ex)=log(wepx+1),0 (8) 其中σi(U)、σi(V)、σi(X)分别是矩阵U、V、X的第i个奇异值. 证明要证明不等式(8)成立,只需要证明函数f(ex)=log(wepx+1)是一个关于x的单调递增的凸函数.对任意x≥0,f(ex)关于x的一阶导数(1/wepx+1)(wpepx)≥0,说明它是一个关于x的单调递增函数;再者,其二阶导p2wepx(wepx+1)-2≥0,说明它是一个关于x的凸函数.由引理1可知,不等式(8)成立. 定理1假设矩阵X∈m1×m2可以分解为X=UVT,其中U∈m1×r,V∈r×m2和rank(X)≤r≤min{m1,m2},则有如下等式成立: (9) 其中c可取(0,2],0 证明首先,根据不等式(8),有如下不等式: 其中第二个不等式由杨氏不等式[8]2ab≤a2+b2,∀a,b≥0可得.根据加权对数范数的定义和rank(X)≤r,可得: (10) (11) 综合式(10)和式(11),定理1结果得证. 除了双因子分解形式,定理1还可以推广到多因子分解形式.在给出结论之前,先给出以下引理: 引理3设有函数fp(ex)=log(wepx+1),x∈[0,+∞),0 n·fc/n(x1x2…xn)≤fc(x1)+fc(x2)+…+fc(xn), (12) 其中p=c/n,n∈N+. 证明 接下来,提出加权对数范数的多因子分解等价定理. 定理2给定矩阵X∈m1×m2,设X可以分解为其中X1∈m1×r1,Xi∈ri-1×ri(i=2,…,n-1),Xn∈rn-1×m2,rank(X)≤ri≤min{m1,m2}(i=1,…,n-1),则有 (13) 其中第一个不等式自然成立;第二个不等式由引理3得到;第三个不等式是基于r≤min{m1,r1},r≤min{m2,rn-1}以及r≤min{ri-1,ri}(i=2,…,n-1).因此,以下不等式成立: (14) (15) 结合式(14)(10)和式(15),定理2结论得证. 在式(2)的秩极小化框架下,使用加权对数范数作为矩阵填充问题的低秩正则化项,考虑高斯噪声,提出如下模型: (16) 根据定理2,上式可以等价地转化为多因子分解形式,模型如下: (17) 其中X1∈m1×r1,Xi∈ri-1×ri(i=2,…,n-1),Xn∈rn-1×m2,而W∈m1×m2表示0-1指示矩阵.式(16)和式(17)中的变量满足如下关系:其中rank(X)≤r≤min{m1,m2}(i=1,…,n-1). 由于式(17)中的耦合变量难以优化,本文应用临近交替极小化框架(Proximal Alternating Minimization, PAM)[9]对模型进行高效求解.在临近交替极小化框架中,不同的优化变量被分解为耦合因子,这些矩阵因子依次进行更新.例如,对于第k次迭代,在固定其他因子的情况下,极小化关于第i个因子矩阵Xi的优化问题: (18) (19) (20) 接下来,讨论子问题式(20)的求解.给定一个矩阵A∈m1×m2,设其进行奇异值分解为A=UAΣAVAT,其中ΣA=diag(σ1(X),…,σmin{m1,m2}(X)).设α>0,考虑如下优化问题: (21) 根据范数的酉不变性,可得 其中Tr(·)表示迹范数,式中的不等式是基于von Neumann迹不等式[12],且当X的奇异值分解使用UA和VA分别作为左奇异向量和右奇异向量时,等式成立.从而,式(21)可以改写为: (22) 其中σi(X)(i=1,…,min{m1,m2})和σi(A)(i=1,…,min{m1,m2})分别是X和A的第i个奇异值. 在问题(22)中,可以使用广义奇异值阈值算子(Generalized Singular Value Thresholding, GSVT)[13]来求解形式如下的问题: (23) (24) 其中xi=σi(X),ai=σi(A),g(x)=αlog(wxc+1). 问题(24)通过GSVT计算最大的局部最小值点为xi,然后比较0和xi处的函数值大小,得到最优解 ∇fai(xi)=0,0 算法:WLMF算法输入:Y∈ℝm1×m2,λ,n,c,μmin,kmax;输出:Xki ;1.初始化:{X0i}={X1i},t1=1,ω1=0,k=1,i=1;2.更新μki=max{L(di(Xki),μmin)},其中L(di(Xki))=‖Qk1,i‖2·‖Qk2,i‖2是di(Xki)的Lipschitz常数;3.更新ωki=min{(tk-1-1)/tk,0.9999μk-1i/μki},其中tk=(1+1+4t2k-1)/2;4.更新[Xki]=Xki+ωki(Xki-Xk-1i);5.根据式(23)更新Xk+1i=UAdiag(Proxg(A))VAT;6.i=i+1;7.若i>n,则k=k+1,i=1;8.若k=kmax或收敛,输出结果,否则转至2; (25) 同时为了验证本文算法的收敛性,提出算法的终止准则是连续两个重构矩阵的相对变化(RelCha)足够小.RelCha表示为: (26) 其中η>0是一个给定的容许值. 表1 不同模型的合成数据修复结果 针对合成数据的修复,构造了一个大小为600×600的秩为30的随机非负矩阵.构造方法为先生成两个大小为600×30的随机非负矩阵U和V,然后两者相乘得到合成矩阵,即X=UVT,并随机抽取5%的元素作为观测矩阵.使用n=2和c=0.8的WLMF进行实验,并设置秩参数r=35.各模型实验结果取十次实验的平均值.表1展示了各模型在合成数据上的实验结果. 从表1的实验结果可以看出本文提出的WLMF算法在对比实验中取得了最好的实验结果,并且与未进行矩阵分解的算法相比,WLMF算法的运行时间要短许多. 为了更好的对比5种算法的修复性能,本文在多张彩色图片上进行图像实验.自然图像通常可以被视为近似的低秩矩阵[1],由于其具有三个颜色通道,因此实验通过矩阵填充算法分别修复每个通道.以图2(见下页)中像素大小为300×300的6张原始图像作为实验对象,随机抽取其像素的15%作为实验的观测矩阵.在实验中,使用n=2和c=0.8的WLMF进行实验,并设置秩参数r=20. 各算法的定量实验结果如表2所示,所有结果均为10次实验的平均值.除了每张图片的修复结果,表中还记录了6幅图像修复结果的平均值和运行时间的平均值.从表2可以看出,本文提出的WLMF算法在所有模型中得分最高.平均而言,它比其他算法有明显的优势.同时,对比各算法的运行时间,可以发现本文提出的算法运行时间较短.另外,图3展示了Image-3在各算法模型上实验的视觉比较.可以更直观的看出,WLMF算法可以更好的修复图像的细节,更接近原始图像. 图2 原始彩色图像 图3 Image3在不同模型下的实验结果 表2 不同模型的彩色图片修复结果 图4 PSNR随秩参数的变化图 为了研究秩参数r对图像修复的影响,进一步测试了具有不同秩参数r的WLMF算法性能.每个场景下PSNR随r的变化如图4所示.可以发现,六张彩色图片实验结果数值总体趋势随着r的增大而增大,并在r=20之后趋于稳定,即使在增大r实验结果也没有明显变化.该结果表明,所提出的WLMF模型对于秩参数的选择具有一定的鲁棒性. 图5是当Image-3的采样率为15%时算法WLMF的RelCha随迭代次数的变化曲线,三条曲线表示三条颜色通道.从变化曲线可以看出,随着迭代次数的增加,RelCha值迅速减小并趋于0,说明WLMF算法具有较好的收敛性. 在本文中,提出了一种加权对数范数矩阵分解算法WLMF来求解矩阵填充问题.该算法结合了秩函数的非凸替代和低秩矩阵分解,使得该算法具有更好的恢复性能,并提高了计算效率.数值实验结果验证了算法的有效性,在整体视觉效果和局部细节保留方面优于对比的经典算法.




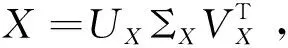
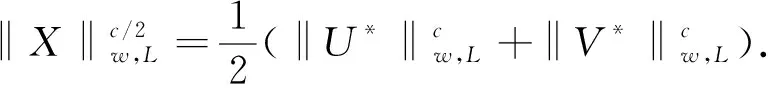
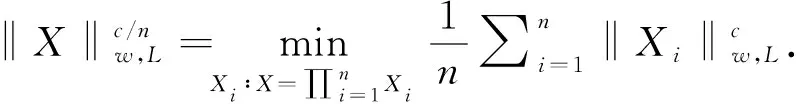


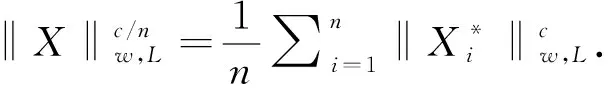
2.2 矩阵填充模型


2.3 模型求解





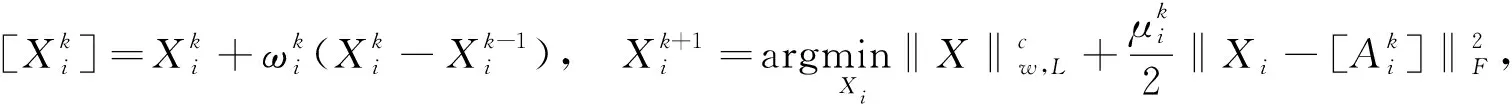

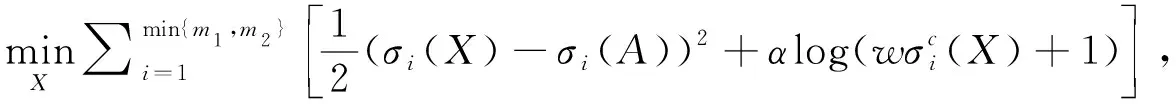



3 实验



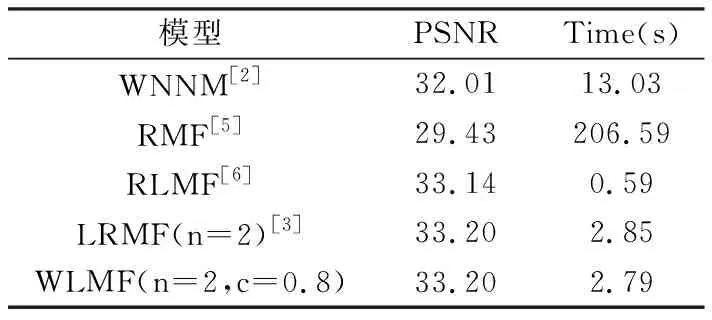
3.1 合成数据修复
3.2 彩色图像修复



3.3 参数灵敏度分析
3.4 算法收敛性
4 总结
