高速公路路隧过渡段施工阶段不均匀沉降关键影响因素分析

韩亚军 HAN Ya-jun；刘滔滔 LIU Tao-tao；姚琴 YAO Qin

（中国电建路桥集团，清远 511500）

0 引言

在高速公路路隧过渡段，隧道一侧仰拱及仰拱回填部分具有较大刚度，而路基一侧为柔性材料，天然含水量相对较高、孔隙比大，刚度较小，在外部荷载作用下，会产生较大的变形，因而路隧过渡段易产生纵向不均匀沉降，轻则影响行车平顺性，重则会引发跳车现象甚至会威胁行车安全。现有研究分析了高速铁路路隧过渡段的线路变形特点及机理、路隧过渡段无砟轨道力学性能、搭接板结构在路隧过渡段中对不均匀沉降的影响[1-3]。目前关于高速公路路隧过渡段尤其是施工阶段不均匀沉降方面的研究较少。本文结合广东地区某高速公路工程实际，建立路基-土体-隧道一体化有限元模型，基于现场过渡段施工方案选取影响参数分析其对路隧过渡段不均匀沉降的影响规律。

1 工程概况

1.1 地形地貌及设计概况

选取某高速公路隧道入口附近路隧过渡段作为研究对象。此段高速公路总体约为东西走向，呈近直线分布，隧道最大埋深约159.53m，隧道采用分离式洞口位于斜坡上，自然山坡坡度约为10°～40°，设计明洞长10m，隧道区属剥蚀丘陵地貌区。

1.2 地层岩性

工点主要地层从上至下依次为：①粉质黏土，揭露层厚2.30～4.50m；②砂质粘性土，揭露层厚0.70～15.00m；③全风化花岗岩，钻孔揭露层厚2.20～17.40m；④强风化花岗岩，钻孔揭露层厚2.60～37.00m；⑤中风化花岗岩，钻孔揭露厚度3.10～42.10m。

2 计算模型

2.1 计算假定

建立高速公路路隧过渡段有限元分析模型时，为简化计算模型、提高计算效率，做出如下假定：①土体为各向同性弹塑性均质体；②计算模型仅考虑重力荷载与车辆荷载对沉降量的影响；③水位不变，不考虑孔隙水压力引起的土体固结；④路基底面、各层土体接触面均简化为平面。

2.2 本构模型及材料属性

本文土体的模拟计算依据摩尔-库仑屈服准则，材料参数主要包括弹性模量、泊松比、天然密度、粘聚力、内摩擦角以及膨胀角等；对于隧道洞口材料以及路基路面材料，选择弹性本构模型进行模拟，其中材料参数主要包括弹性模量、泊松比、天然密度等，表1为路隧过渡段模型材料参数表。

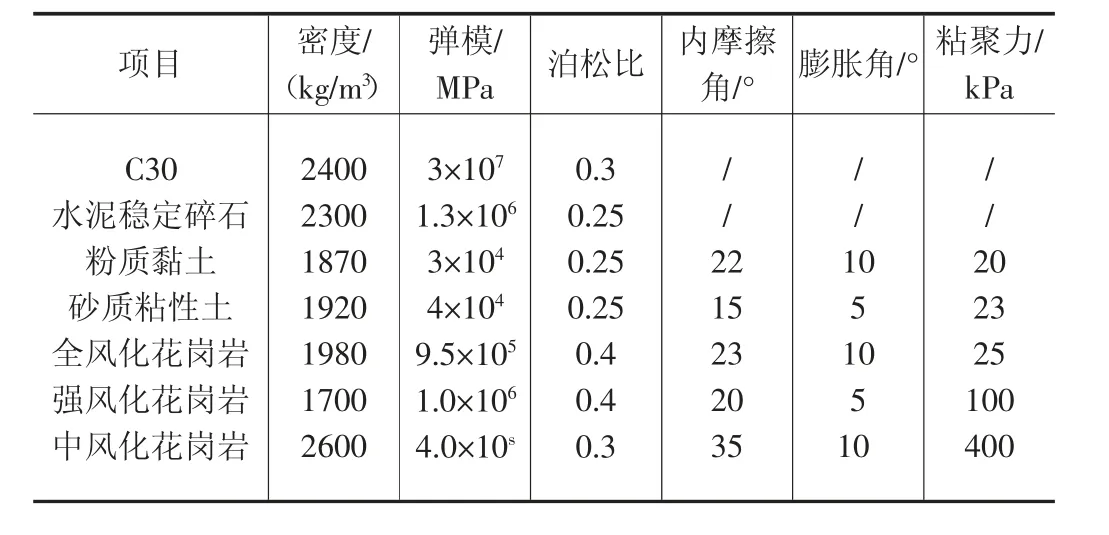
表1 材料参数表

2.3 边界条件及接触条件

根据研究地段路基和隧道的受力与约束情况，有限元模型边界条件设置为：y方向为竖直方向，地基底部施加全约束（各方向位移均为0），两侧面施加z方向的位移约束，正面和背面施加x方向的位移约束；顶部为自由面，只考虑上部重力与车辆荷载引起的竖向应力和位移变化。

有限元模型中接触方式全部设置为硬接触，即两物体之间的穿透量为0；各土层之间均采用摩擦接触，从最顶层自上往下摩擦系数依次采用0.35、0.3、0.4，0.3。

2.4 网格划分及荷载条件

为提高有限元模型计算精确性，对有限元模型中路基及仰拱部分进行网格加密，另外由于隧道与土体进行接触，受力较为复杂，故对隧道与土体接触部分的网格也进行加密处理。网格单元类型设置为C3D8R，有限元模型网格总数为21530，节点数为31420。

对土体、隧道、路基路面部分施加重力荷载，并将车辆荷载简化为20kPa的均布荷载，施加在路面上。

建立的高速公路路隧过渡段有限元模型如图1所示。

图1 路隧过渡段有限元模型

对比分析有无车辆荷载对路隧过渡段沉降量的影响，计算结果见图2。

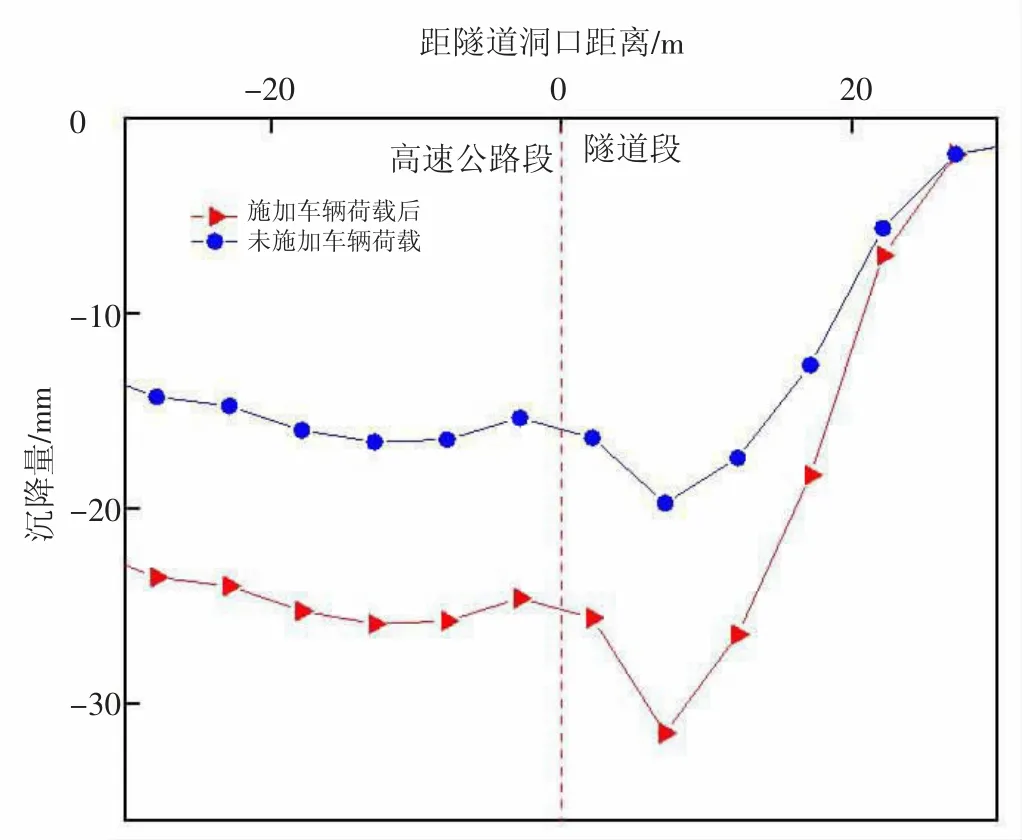
图2 施加车辆荷载前后沉降量对比

由图2可知，在施加车辆荷载后最大沉降量和最大不均匀沉降量有显著增长。在车辆荷载作用下，最大沉降量为31.5mm，最大不均匀沉降由3.6mm增长到了5.9mm。车辆荷载对沉降量影响不可忽略，故在下文分析中均考虑施加车辆荷载。

3 不均匀沉降影响因素分析

3.1 搭板

计算分析时，搭板厚度采用0.3m，搭板长度采用6m，与隧道端搭接长度分别取为0.5m、1m、1.2m、1.5m、2m。计算结果如图3所示。

由图3可知，在搭接长度取1m时，原最大沉降位置处沉降量减少了9.0mm，且最大不均匀沉降量为3.8mm。但与隧道搭接长度超过1.2m后，隧道内部约2m处沉降量会显著增大，当搭接长度取2m时，该处沉降量增长了14.5mm，且最大不均匀沉降量为15.1mm，对路隧过渡段沉降有负面效应。故与隧道端搭接长度取0.5～1m时，对沉降量及最大不均匀沉降量的控制效果更为良好。

进一步研究搭板长度对路隧过渡段沉降的影响。分析时，搭板与隧道搭接长度取1m，搭板厚度取0.3m，搭板长度分别取4m、5m、6m、7m、8m。计算结果见图4。

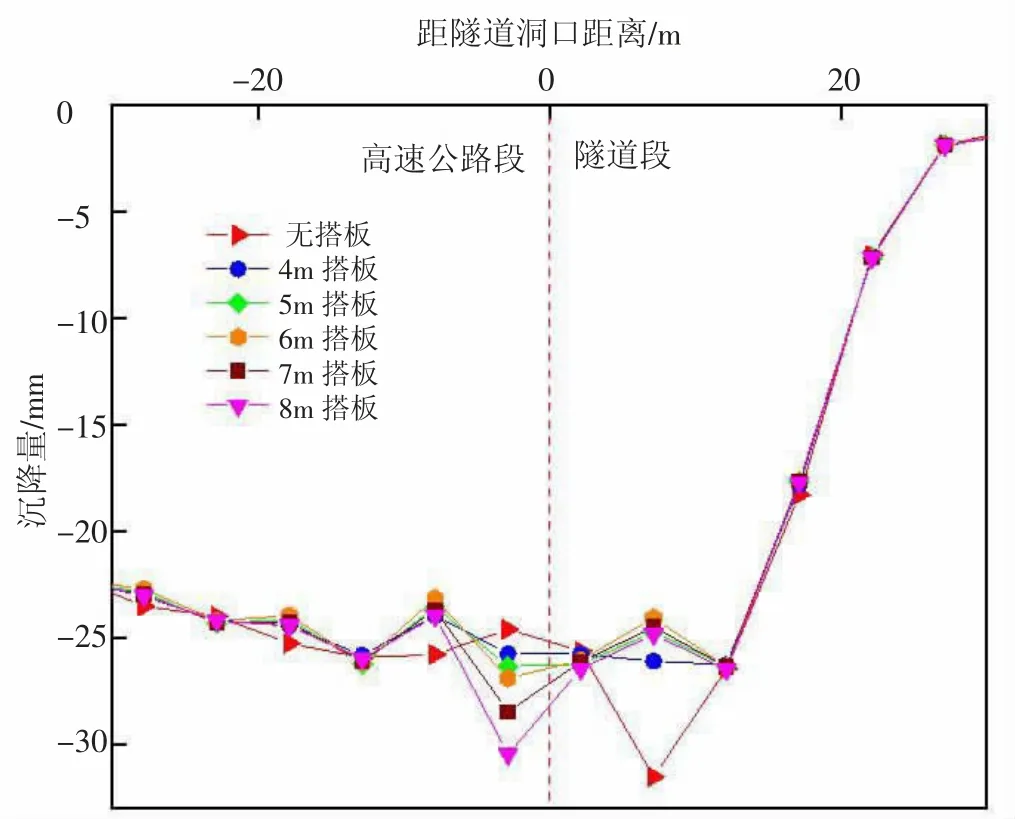
图4 改变搭板长度沉降量对比

由图4可知，设置搭板结构后，隧道洞口前约7m处沉降量、原最大沉降量位置处沉降量均有所减小，在搭板长度取6m时，减小量为7.5mm，最大不均匀沉降量为3.8mm。隧道洞口前约2m处沉降量在设置搭板后增大，挡板长度超过6m，隧道洞口前约2m处的沉降增量变化显著，当搭板长度取8m时，此处沉降量增大了5.9mm，且最大不均匀沉降量为6.5mm。故搭板长度取在4～6m，对沉降量的控制有较为适宜的效果。

3.2 路基材料

实际工程中路基材料使用的是水泥稳定碎石，密度为2300kg/m3，弹性模量为1300MPa，泊松比为0.25，现在保持其他条件不变，分别采用改变材料密度、材料弹性模量来对沉降量进行分析。

保持路基材料的弹性模量及其他条件不变，密度分别取2300kg/m3、2600kg/m3、2900kg/m3来对沉降量进行分析。计算结果见图5。

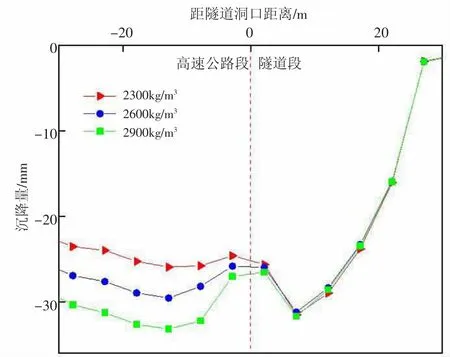
图5 改变路基材料密度沉降量对比

由图5可知，随着路基材料密度的增大，高速公路段的最大沉降量随之增大，密度取2300kg/m3、2600kg/m3、2900kg/m3时，高速公路段的最大沉降量分别为25.9mm、29.5mm、33.1mm，最大不均匀沉降量分别为5.9mm、5.5mm、5.2mm。

保持路基材料的密度及其他条件不变，弹性模量分别取1300MPa、1600MPa、1900MPa来对沉降量进行分析。计算结果见图6。

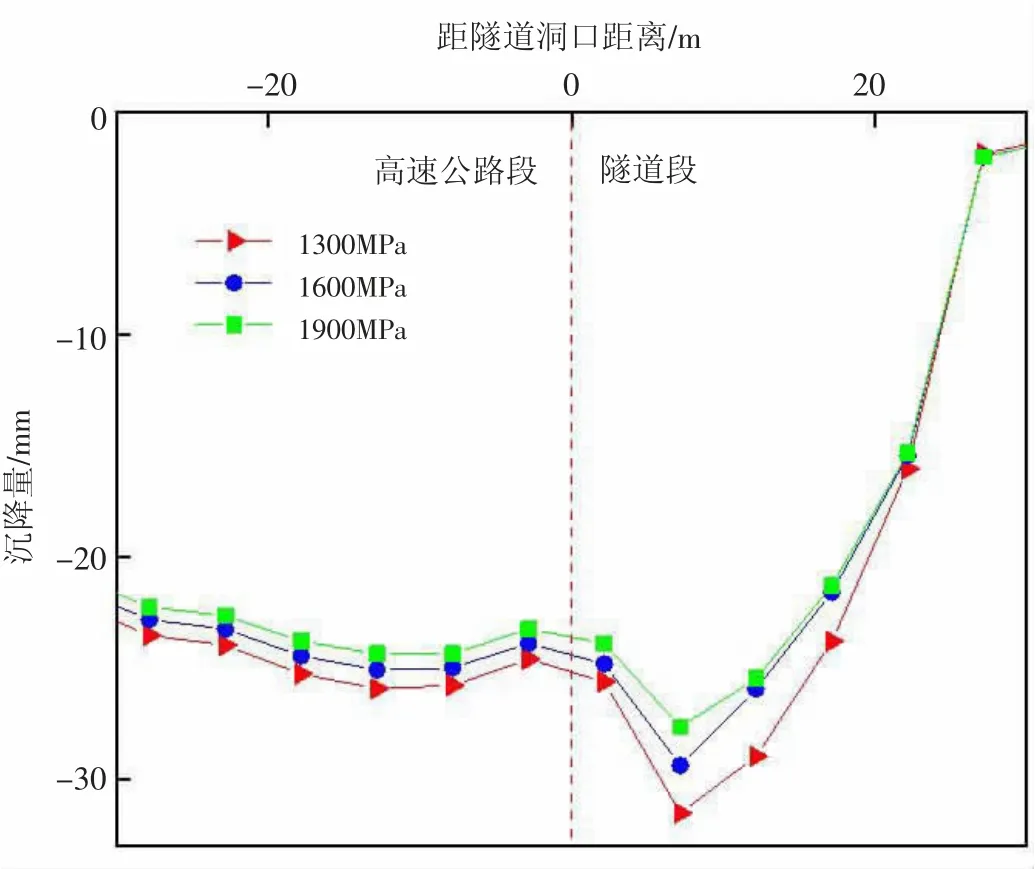
图6 改变路基材料弹性模量沉降量对比

由图6可知，当路基材料弹性模量取1600MPa、1900MPa时，原最大沉降位置的沉降量分别减小了2.2mm、3.9mm，最大不均匀沉降沉降量分别减少为4.6mm和3.8mm。

3.3 路面铺装层厚度

原工程路面铺装最顶层及次顶层为SAM-13层和CAG-20C层，其厚度分别为4cm和6cm，现通过改变SAM-13层、CAG-20C层厚度的方式来对沉降量进行分析。计算结果见图7。

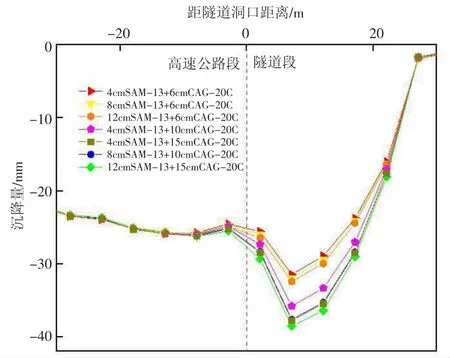
图7 改变SAM-13层、CAG-20C层厚度沉降量对比

由图7可知，在同时增加两层厚度时沉降量有显著的变化，但是在仅增加SAM-13层厚度时沉降变化量非常微小，可以进一步说明次顶层CAG-20C厚度的改变对沉降量有较大的影响。

4 结论

本文建立路基-土体-隧道一体化有限元模型，分析了搭板、路基材料、路面铺装层厚度变化对路隧过渡段不均匀沉降的影响规律，主要结论如下：①设置搭板结构对控制路隧过渡段沉降有良好的效果，但搭板与隧道端搭接长度应控制在0.5～1m范围内，搭板长度应控制在4～6m范围内，对沉降的控制量可以达到9mm，可将最大不均匀沉降量控制到3.8mm，搭接长度过长、搭板长度过长都会对沉降量及不均匀沉降量有不良影响。②路基材料密度增大沉降量会随之增大，路基材料弹性模量增大沉降量会随之减小，在路隧过渡段采用密度相对较小、弹性模量相对较大的路基材料，可以在一定程度上控制路隧过渡段的沉降量及不均匀沉降量。③改变路面铺装最顶层厚度对沉降量影响较小，但改变次顶层厚度对沉降量影响较大，仅改变次顶层CAG-20C厚度且取15cm时，最大沉降量可达到6.3mm，最大不均匀沉降量可达9.3mm，故路面铺装次顶层厚度不宜采用过厚。