拉格朗日插值法在铁路货运量的探究与应用

文/马萱航 孙语聪 罗纯

铁路运输在整个运输领域中占有重要的地位，并发挥着愈来愈重要的作用，在一定程度上反映了我国经济发展水平。考虑到铁路货运量影响因素较多导致预测准确性较低的问题，提出基于拉格朗日插值的灰色GM（1，1）模型预测铁路货运量数据，并推算避免龙格现象的改进拉格朗日插值预测模型，预测结果表明，所提预测方法能够有效提高预测精准度，铁路运输效率较好。

0.引言

铁路货运在我国交通运输行业中的位置和作用至关重要，铁路货物运输是我国的经济命脉。国外一些国家较早地对铁路货运量就展开研究并得到相关结论。文献[1]中考虑到对于铁路货运量影响因素的作用力不同，利用神经网络构架铁路货运量影响因素图表并进行预测分析；文献[2]中首次提出将Box-Jenkins模型运用到铁路货运量的预测中，得到了较为准确的结果。铁路货运量的大小受到社会、自然环境和经济等因素影响，且相关数据不够完善，准确的判断并分析所有的影响因素存在较大难度，使得传统方法如线性回归模型、时间序列分析模型等对铁路货运量的预测一直无法达到较好的拟合效果。灰色GM（1，1）模型以贫信息、小样本为研究对象，提供了不确定性系统解决问题的新思路[3]。如果将铁路货运量看做是一个灰色系统模型，对可以被监测到的铁路货运量进行累加变换，得到一个指数增长模型后进行预测，得到结果再将累加模型以此进行累减还原原数列，从而得到一个对铁路货运量的未来预测值。传统GM（1，1）模型基本思想是:为方便数学建模，对原序列进行一次累加生成，因累加后序列具有指数增长趋势，所以利用近似一阶微分方程建立模型，最后由建模序列累减生成预测序列完成原序列发展趋势的预测[4-5]。

1.灰色GM（1，1）模型

1.1传统GM（1，1）

传统GM（1.1）具体建模过程如下：

设原始数据序列AGO为

X（0）={X1（0），X2（0）X3（0），…，Xn（0）}，n=1，2，3……

对原始数据X（0）做一次累加，得到新序列1-AGO

X（1）={X1（1），X2（1）X3（1），…，Xn（1）}，n=1，2，3……

构造数据矩阵B及数据向量Y，定义白化模型

1.2传统灰色模型误差分析

传统GM（1，1）建模时，原始数列中并不能直观体现其规律性，而对其累加后可以得到具有明显指数增长规律的新数列，此建模方式没有考虑到累加得到的数据也只是近似指数增长的数列，而非完全指数增长，在这个过程中会产生较大误差，无法准确拟合原序列，预测精度并不理想。由于对于累加数列所求得的微分方程只能近似看做指数增长，在这个过程中，曲线的弯曲程度直接影响了模型的精度，却无法对曲线进行预知，图像说明如下。

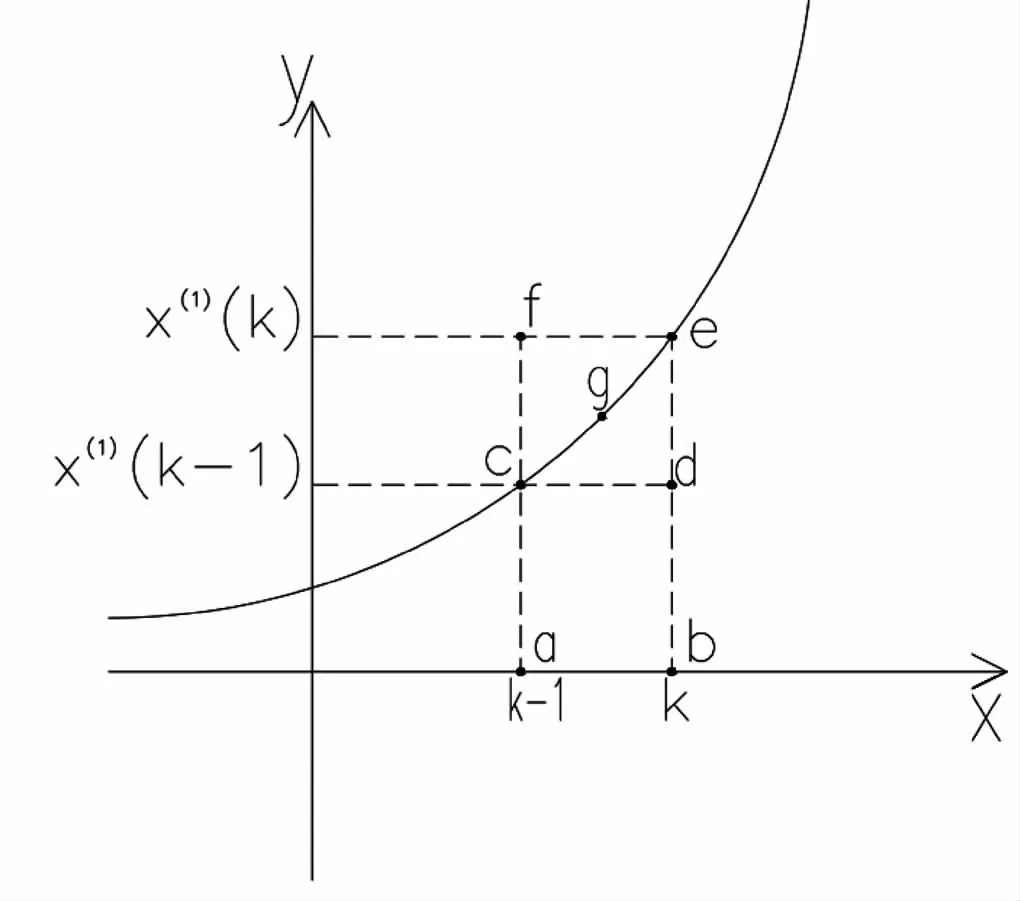
图1 灰色预测模型白化表示

同时考虑到拉格朗日插值拟合的过程中会出现龙格现象导致预测结果出现偏差，由此，再对拉格朗日插值进行改进。

对区间[k，k+1]求其插值函数可以得到

2.实证分析

本文选取中国货运量2000-2020年的数据进行建模分析，数据来源为国家统计局中国统计年鉴[8]。用2000-2015年的相关数据测算得到GM（1，1）预测模型，对2016-2020年的货运量总量进行验证从而预测未来三年的数据，采用前文所叙述的原理和方法进行分析，利用MATLAB建立模型计算结果如下。

表1.2000-2015年我国铁路货运量总量（万吨）

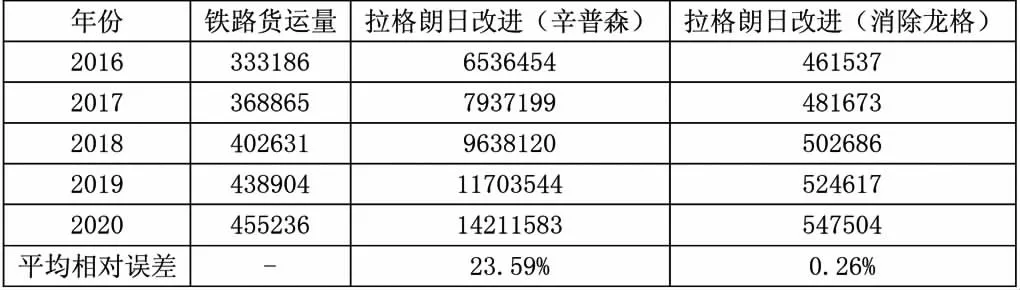
表2.2016-2020年我国铁路货运量（万吨）预测结果

由此可以对比看出，经过改进拉格朗日插值的GM（1，1）预测模型精度相比拉格朗日插值GM（1，1）有所提高，有着更高的精度，采用上述基于改进拉格朗日插值改进的灰色模型进行预测未来5年我国铁路货运量总量情况如下表所示。

表3.2021-2025年我国铁路货运量（万吨）预测

根据原始数据和预测结果显示，可以看出未来我国铁路货运量总量将不断上升，这与我国铁路的不断完善有着密不可分的关系，数据从2000年的178581万吨到2020年的455236万吨，预测结果显示未来铁路货运量仍然会持续增长，尤其随着我国铁路线路的增多和延长，我国铁路货运量将会迎来新的高峰。

3.结语

本文基于拉格朗日插值灰色预测模型对白化背景值进行分析，提出消除拉格朗日插值造成的龙格现象的改进拉格朗日插值灰色GM（1，1）预测模型，并对我国铁路货运量总量进行实证探究和分析，改进模型所得到的结果具有一定的科学性，可为我国铁运相关部门的科学决策提供一定的理论依据和参考价值。C

引用出处

[1].KLODZINSKI J，AL-DEEK H.Transferability of an intermodal freight transportation forecasting model to major florida seaports[J].Transportation R esearch R ecord Journal of the Transportation Research Board，2003，1820:36-45.

[2].CULLINANE K P B，MASON K J，CAPEM.A comparison of models for forecasting the baltic freight index:box-jenkins revisited[J].International JournalofM aritime Economics.1999（1）:15-39.

[3].曾祥艳.灰色预测GM（1，1）模型的几种拓广模型研究[D].成都:电子科技大学，2016.

[4].N ING X U，DANG Y.Characteristic adaptive GM（1，1）modeland forecasting ofChinese traffic pollution em ission[J].SystemsEngineering-Theory＆Practice，2018，38（1）:187-196.

[5].刘思峰等.GM（1，1）模型的几种基本形式及其适用范围研究[J].系统工程与电子技术，2014，36（3）:501-508.

[6].张春晓，陈又圣，黄鸿展.基于拉格朗日插值的电子耳蜗分数延迟和参数失配分析[J].中国医学物理学杂志，2021，38（04）:468-471.

[7].钟凯强，周建平，薛瑞雷，熊莹.一种采用Lagrange插值的相贯线简化算法[J].热加工工艺，2021，50（15）:131-135+140.

[8].中华人民共和国统计局.中国统计年鉴[M]北京：中国统计出版社，2020.