基于鲁棒优化的数控加工工艺参数优化研究＊

2023-12-13杨文宜李伯棠陈杰新

科技与创新 2023年23期

杨文宜，李伯棠，陈杰新

（1.广州航海学院实验中心，广东广州 510725；2.广州航海学院港口与航运管理学院，广东广州 510725）

如今，随着数控工具自动化程度提高，对工具结构的需求不断增加，参数也发生了变化。在数控和单批机械制造中，工具磨损工具也会增加切割强度切削力[1]和切削功耗[2]，能源消耗可达到40%[3]。同时，在一次操作中选择各种技术标准将导致工具磨损率的显著差异[4]，更换磨损工具也将改变组合最佳能效参数的过程[5]。

在数控和机械制造过程中，选择合理的刀具来提高机器效率和节能非常重要。最近，许多学者开始研究该问题，如ZHOU 等[6]针对独立地优化切削参数和刀具路径，提出了一种新的多目标优化模型；SAHA等[7]使用500 μm TiAlN 涂层WC/6Co 立铣刀对Ti-6Al-4V 进行微铣削过程中工艺力学、材料变形机制、刀具几何形状、润滑和工艺参数的累积影响；CAPⅠK 等[8]研究了钻头寿命与岩石力学、可钻性和研磨性之间的关系及钻头磨损类型；LⅠN 等[9]分析了切削参数对铣削力、铣削温度和表面粗糙度的影响，提出了一种基于非支配排序遗传算法和层次分析的综合优化模型；SEVERⅠNO 等[10]提出了一种可以识别零件形貌并确定铣削腔的最佳刀具直径集算法，以解决因为相对较大的刀具直径减少铣削时间的问题。

在现实中，不确定性是引起数控加工过程困难的主要原因之一，但相关研究较少，如龚肖新等[11]构建了模具数控加工切削参数优化方案模糊模型。但模糊模型的缺点在于可能存在约束间的冲突，从而导致决策错误。为了应对该问题，BEYER 等[12]开始采用鲁棒优化理论研究，BERTSⅠMAS 等[13-14]基于之前的研究，建立了一个改进的鲁棒优化框架。

综上，在数控批量加工生产的过程中，考虑刀具使用寿命的不确定性和工艺参数组合的均衡状态对加工过程中能源使用效率的影响，对工艺加工机制和能源使用效率的特点进行研究。

1 问题描述

数控加工过程中，加工工艺参数是需要进行组合优化的问题。参数的组合影响着数控处理过程中的切削功耗和加工物品表面去杂质的效率[15]，进而加大了刀具磨损程度。需要适时调整参数来减少能耗并提高生产效率。实际生产作业中，参数的变化可能会引起数控加工过程的变化，使制造企业面临巨大的风险。因此，本文设定考虑刀具使用寿命具有不确定性，参数的变化用对称区间表示。在上述条件下，建立以最短切削加工时间为目标的单特征零件批量加工非线性规划模型；然后针对刀具使用寿命不确定的情况，建立基于鲁棒优化的数学模型，分析不确定参数的变化对工艺参数的影响。

2 模型建立

2.1 目标函数

工序加工时间包括切削时间、换刀时间和工艺辅助时间。加工时间最短的切削数量能够实现最高的生产效率。最小化切削加工过程时间的公式如下：

式中：d0为工件直径的数值；Lw为加工长度的数值；Δ为加工余量的数值；asp为切削深度的数值；vc为切削速度的数值；f为进给量的数值；x、y、z为刀具寿命系数的数值；CT为与切削条件有关的常数的数值；tot为换刀之外的辅助时间的数值。

2.2 约束条件

约束条件具体如下：

式中：nmin、nmax为机床主轴最低和最高转速的数值；fmin、fmax为机床的最小进给量和最大进给量的数值；为与工件材料和切削条件有关的系数；Fmax为最大进给力的数值；Fc为切削力的数值；η为机床功率有效系数；Pmax为机床最大有效切削功率的数值；r为刀具直径的数值；Rmin为零件表面粗糙度要求的最小值；Cv、Kv、xv、yv、sv、qv、pv、l分别为相关加工系数；ap为背吃刀量的数值；ae为侧吃刀量的数值；z为齿数的数值；N为重磨次数的数值；T为道具寿命的数值；α、β为辅助时间的相关系数的数值。

式（2）限制主轴转速的最大和最小转速的范围；式（3）限制进给量在最小和最大进给量之间，式（4）限制切削进给抗力小于或等于所允许的最大进给力，式（5）表示机床功率应小于规定的最大有效切削功率，式（6）限制加工过程中的零件表面粗糙度小于或等于零件质量的最低粗糙度要求，式（7）表示数控加工过程中必须考虑到刀具使用寿命，式（8）表示辅助时间与切削速度、进给量的关系，限定变量不小于0。

3 鲁棒优化模型建立

在实际数控加工过程中，很难把握刀具使用寿命的时间量，往往这些不确定因素会造成数控加工工艺参数优化困难，导致额外成本增加，所以需要考虑刀具使用寿命T不确定的情况，根据文献[12-14]的处理方法，把T看作一个有界对称的随机变量，取值为，这里T代表需求量的名义值，为名义值的最大偏差值。为了控制道具寿命的鲁棒性，本文引入新的参数取值范围为[0，1]，用于调整模型的保守性，不一定取整数。由式（7）发现，不等式的右端只有一个参数，所以这里代表T的保守度的变化程度，根据鲁棒优化方法得到式（7）的鲁棒对应式：

式中：w1和r1为根据对偶理论所增加的变量。

从以上分析得到的对应鲁棒优化模型是以式（1）为目标，以式（2）—式（10）为约束条件的非线性规划模型。

4 案例分析

为了证明所建立鲁棒优化模型的有效性，本文应用一个案例进行分析，使用软件MATLAB 中的YALMⅠP 工具包进行计算，具体数据如下：①数控车床规格参数。主轴最低转速nmin为93 r/min，主轴最高转速nmax为1 600 r/min，最小进给量fmin为0.25 mm/r，最大进给量fmax为3.6 mm/r，最大切削力Fmax为11 000 N，最大有效切削功率Pmax为19 kW，机床功率系数η为0.95。②其他参数。工件材料为46 钢棒，切削深度asp为2 mm，加工质量要求轮廓算数平均偏差不超过6.3 μm，加工时使用切削液，刀具的刀尖圆弧半径rε为0.9 mm。由切削用量手册可以得出刀具寿命为64 243 h，取800，α和β分别取0.3 和0.5，其他系数如表1 所示。为了测试所建鲁棒模型的稳定性，设置保守度Γ分别为0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0，运算结果如表2 所示。

表1 刀具寿命及切削力系数表

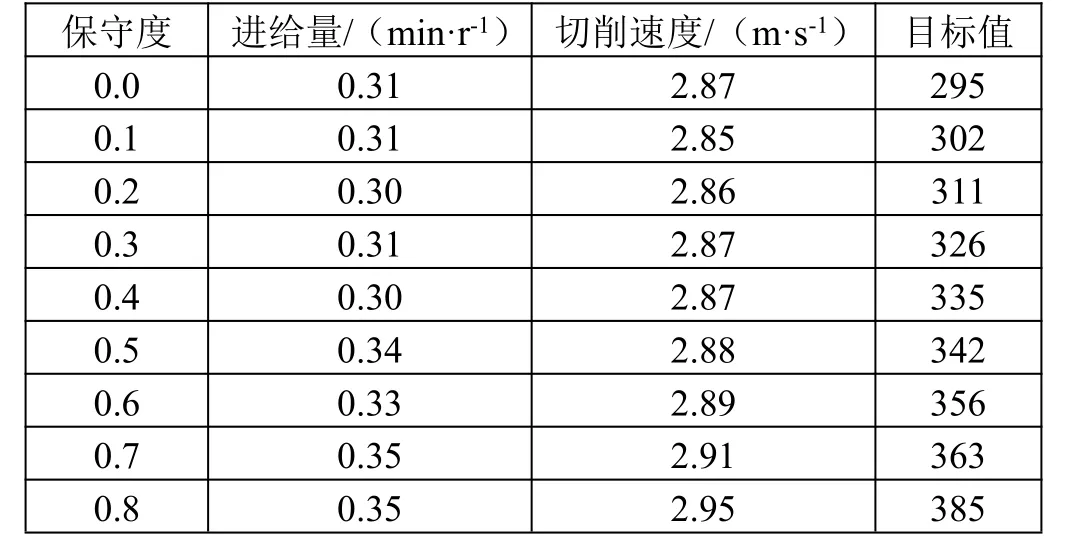
表2 不同保守度水平下目标值的对比

由表2 可知，随着保守度的增加，扰动的范围变大，模型的目标值递增。这是因为所属的集合变大，模型可行域变大使得目标值变大，说明了鲁棒模型的保守性与其最优性成反比。对于最保守情况下的鲁棒优化模型，虽然保守性增强而最优性降低了，而在刀具寿命发生变化的时候，模型的解仍然可以有效地应用于数控加工流程，给出的决策体现了实用性和有效性，证明所提鲁棒优化模型符合实际要求。