基于优化算法的波浪能装置最大输出功率设计
2023-12-13王骥源贺冠翔赵书玲
王骥源,贺冠翔,赵书玲
(江西理工大学电气工程与自动化学院,江西 赣州 341000)
波浪能是一种重要的海洋可再生能源,分布广泛,储量丰富,具有可观的应用前景,如何将波浪能最大化地转化利用成为新能源领域的热门话题。波浪能转换装置有液压式、气压式、机械式3 种形式,李燕等[1]研究表明,液压式波浪能转换装置由于转换效率高、输出稳定,为首选波浪能转换装置。液压式装置又可细分为点头鸭式、摇摆式、阀式、振浮式4 种,其中振浮式应用研究最广,振浮式波浪能装置主要通过垂荡和纵摇获取并转换波浪能[2]。对于此类装置输出功率的优化,国内做了不少研究,已有的相关研究中,研究人员通常借助软件仿真、算法优化等方式找出相应的最大输出功率。潘海鹏等[3]基于遗传算法对以浮子为驱动装置的直驱式海浪发电系统的最大功率进行跟踪控制,此方法可大幅度提升发电系统对波浪能的捕获效率;黄俊豪等[4]借助WFT 法获取波浪能发电系统最大功率的捕获条件,并结合Simulink 仿真,最终提升了使得系统功率输出的优化效果;杨俊华等[5]根据商用软件求解浮子的非线性参数,结合改进型的鲸鱼算法,优化了相应负载参数,进而提高了波浪能捕获效率。
本文根据振浮式波浪能转换装置垂荡和纵摇这2 种运动方式,并建立该装置运动和功率模型,在此基础上进行数值求解和算法优化,设计出了实现波浪能装置输出功率最大化的最优系统参数,为实际应用提供参考。
1 问题的提出及理论依据
图1 为振浮式波浪能装置示意图,由浮子、振子、中轴及能量输出系统(简称“PTO 系统”,包括弹簧、直线阻尼器、扭转弹簧、旋转阻尼器和转轴)等构成。在波浪激励力和波浪激励力矩作用下,浮子同时进行垂荡和纵摇,并通过PTO 系统使振子沿着中轴进行垂荡和纵摇。除此之外,浮子在线性周期微幅波作用下[6],还受到附加惯性力和附加惯性力矩、兴波阻尼力和兴波阻尼力矩、静水恢复力和静水恢复力矩的影响。振子沿中轴垂荡时,直线阻尼器的阻尼力与浮子和振子的相对速度成正比,比例系数为直线阻尼器的直线阻尼系数;振子沿中轴纵摇时,旋转阻尼器的扭矩与浮子和振子的相对角速度成正比,比例系数为旋转阻尼器的旋转阻尼系数,2 个阻尼系数在[0,100 000]区间取值。浮子和振子通过相对垂荡运动和相对纵摇运动驱动直线阻尼器和旋转阻尼器做功,并将所做的功作为该波浪能装置的能量输出。结合相关条件,计算出波浪能装置输出的最大功率,并确定该功率下直线阻尼器的阻尼系数和旋转阻尼器的阻尼系数。分析问题时,考虑海水是无粘无旋的,忽略中轴、PTO 的质量和各种摩擦。

图1 振浮式波浪能装置示意图
遗传算法最早由美国的JOHO 于20 世纪70 年代提出,该算法起源于对生物系统所进行的计算机模拟研究,是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算将问题的求解过程转换成生物进化中染色体基因的交叉、变异等过程。它的大致实现过程为从任意初始种群出发,通过随机选择、交叉和变异操作[7],产生一群更适合环境的个体,使群体进化到搜索空间中越来越好的区域,这样多代繁衍进化,最后收敛到一群最适应环境的个体,求得问题最优解。
2 数值模型
2.1 垂荡运动状态分析
装置受力情况如下。
振子进行垂荡时,只受PTO 系统力,而PTO 系统力包含弹簧力和直线阻尼力,具体受力情况如图2 所示。

图2 振子受力图
振子的受力方程如下:
式中:F1为振子所受合力的数值;FPTO为PTO 系统力的数值;Fc为弹簧力的数值;Fx为旋转阻尼器的阻尼力的数值。
结合上文可知,浮子受力情况如图3 所示。
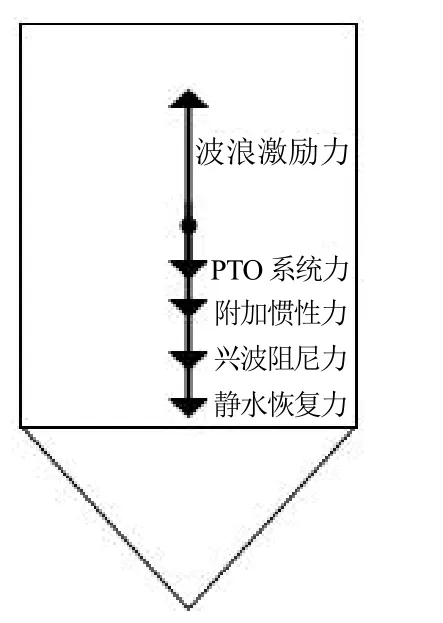
图3 浮子受力图
波浪激励力可表示为:
式中:f为波浪激励力振幅的数值;ω为入射波浪频率的数值。
结合浮子的受力情况,并根据牛顿第二定律,可以列出浮子的垂荡运动方程为:
式中:mb为浮子质量的数值;m′为垂荡附加质量的数值;为浮子垂荡运动加速度的数值;Fb为兴波阻尼力的数值;Fl为静水恢复力的数值。
同理,振子的垂荡运动方程为:
式中:Cz为直线阻尼系数;为浮子垂荡运动速度的数值;为振子垂荡运动速度的数值;Kc为弹簧刚度的数值;xb(t)为浮子垂荡位移的数值;xv(t)为振子垂荡位移的数值。
2.2 纵摇运动状态分析
装置所受力矩如下。
类比垂荡,振子进行纵摇时,受到的力矩如下:
式中:M1为振子所受力矩的数值;MPTO为PTO 系统力矩的数值;Mc为弹簧扭矩的数值;Mx为旋转阻尼器的阻尼扭矩的数值。
结合上文可知浮子受到的力矩,并根据刚性力学中的转动定律,可以列出浮子的纵摇运动方程为:
式中:Ib为浮子转动惯量的数值;I′ 为纵摇附加转动惯量的数值;为浮子角加速度的数值;Mw为兴波阻尼力矩的数值;Mj为静水恢复力矩的数值。
振子的纵摇运动方程为:
式中:Iv为振子转动惯量的数值;为振子角加速度的数值;Kx为旋转弹簧刚度的数值;θb(t)为浮子角位移的数值;θv(t)为振子角位移的数值;Cx为旋转阻尼系数的数值;为浮子角速度的数值;为振子角速度的数值。
2.3 波浪能输出功率
该装置垂荡时,由直线阻尼器和弹簧组成的PTO系统对外做功,因为该装置并非是受到恒力运动,结合微元法和积分法,给出相应的功率公式如下:
该装置纵摇时,由旋转阻尼器和扭转弹簧组成的PTO 系统对外做功,该装置纵摇时受到的力矩亦非平衡,同理,输出功率公式如下:
结合式(1)和式(2)可知,该装置对外输出的总功率如下:
3 数值计算和结果分析
3.1 转动惯量的确定
在求解最大功率前,为确定装置纵摇运动对应的常量参数,需先求出浮子和振子的转动惯量,求解过程如下。
先建立浮子的直角坐标系,如图4 所示。
再确定浮子质心。分别确定圆柱和圆锥对应质心坐标Z1和Z2,结合质心运动定理,可得浮子的质心坐标:
然后确定浮子面密度:
式中:ρb为浮子面密度的数值;mb为浮子质量的数值;L圆柱为圆柱半径的数值;L圆锥为圆锥半径的数值。
圆柱侧面和圆锥侧面转动惯量计算如下:
式中:I1为圆柱侧面转动惯量的数值;I2为圆锥侧面转动惯量的数值。
最后,结合平行轴定理[8],可求得圆柱侧面和圆锥侧面对于质心轴的转动惯量之和,即浮子的转动惯量,公式如下:
式中:d1为圆柱质心到浮子质心距离的数值;d2为圆柱质心到浮子质心距离的数值。
同理,可求得振子转动惯量:
3.2 最大输出功率的计算
求得转动惯量后,结合浮子振子的运动模型和输出功率的模型,引入波浪能装置的常量参数(如表1所示)和直线阻尼系数、旋转阻尼系数这2 个变量参数,编写优化算法,求解该波浪能装置的最大输出功率。
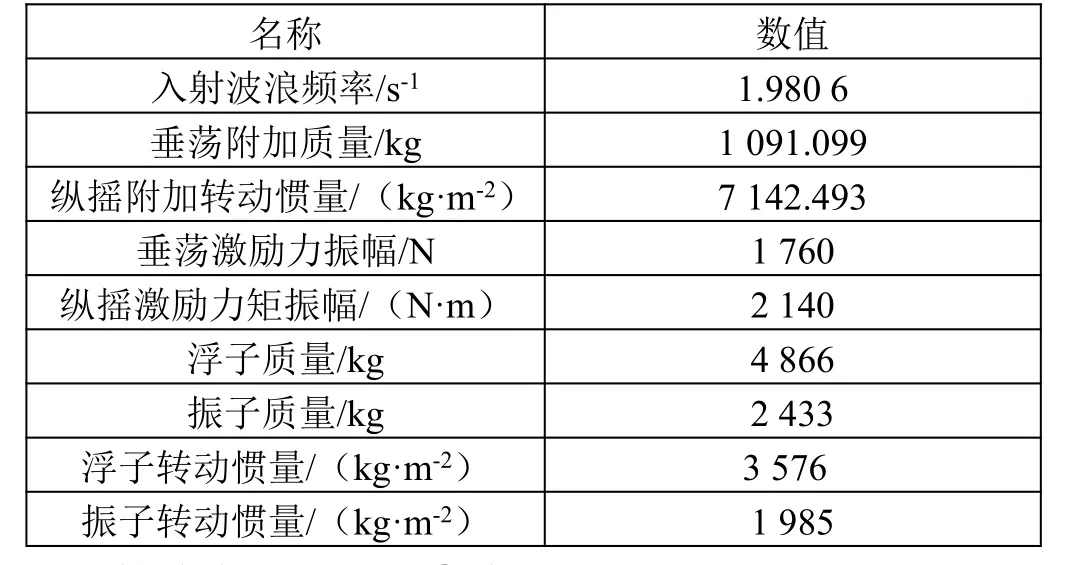
表1 波浪能装置的常量参数
算法步骤如下:①给出求解浮子振子运动状态的算法框架1。将浮子和振子垂荡和纵摇2 个运动对应的微分方程模型导入Matlab 的ode45 函数中,设定浮子和振子的初始位移和速度均为0,运动总时间为184.2 s,步长为0.2 s,最终可求得浮子和振子各自在0~184.2 s 内每隔0.2 s 的速度,由于尚未代入变量值,暂时无法求解。②在框架1 的基础上,结合式(3)和式(4),先离散化计算每隔0.2 s 波浪能装置对外所做的功,再通过数值积分计算出0~184.2 s 所做出的总功,并除以总周期,最终给出求解输出功率所需要的算法框架2。③设定GA 工具箱的初始参数,具体设定为lb=[0,0],表示2 个变量下限;ub=[100 000,100 000],表示2 个变量上限;PopulationSize=10,表示种群数量;Tolfun=1e-3,表示允许误差;CrossoverFraction=0.75,表示交叉率;EliteCount=2,表示每次遗传中的筛选个数;Generation=20,表示迭代遗传次数。④将步骤②中编写好的算法框架2 导入设置好参数的GA 工具箱,并开始运行,最终求得结果。
3.3 结果分析
GA 收敛图如图5 所示。根据图5 可以看到GA 算法的收敛效果较好。

图5 GA 收敛图
波浪能装置输出的最大功率最终收敛于315.77 W,相应的最优直线阻尼系数为589 00 s/m,最优旋转阻尼系数为95 541 s/m。
为了验证结果的可行性,以时间为自变量、位移为因变量,给出浮子振子在最优直线阻尼系数下的垂荡运动状态图,如图6 所示。
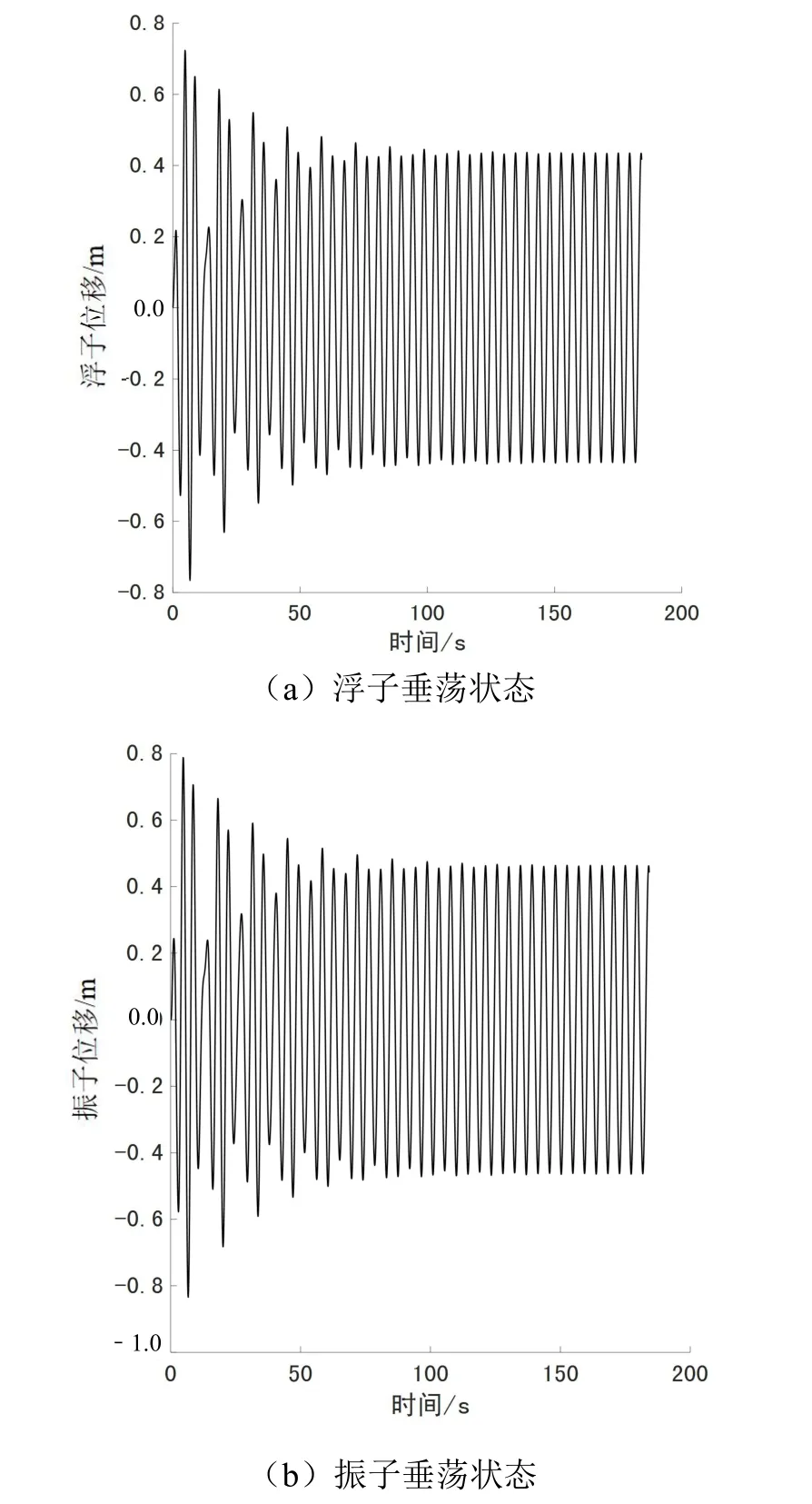
图6 垂荡运动图
由图6 不难看出浮子和振子垂荡状态类似波浪进行简谐运动的状态。除了垂荡,再以时间为自变量、角位移为因变量,给出浮子振子在最优旋转阻尼系数下的纵摇状态图,如图7 所示。

图7 纵摇运动图
纵摇运动也类似波浪的简谐运动。结合遗传算法收敛图和装置运动状态图,最终可以较好地验证该最优系统参数的可行性,并与实际情况相符合。
4 结束语
本研究结合运动学和能量转换等理论建立振浮式波浪能装置输出功率的数学模型,利用Matlab 编写智能优化算法,对实现装置输出功率最大化的最优变量参数进行搜索。经Matlab 的可视化检验,最终得出切合实际情况的最大输出功率和2 个最优阻尼系数,为实际推广应用提供一定参考。
但此研究仍有不足之处,如在实际情况中,波高与风力的影响不能忽略不计,尤其是在纵摇过程中,风力矩带来的影响不可忽略。其次,垂荡与纵摇具有强耦合性,即垂荡必然伴随着纵摇,发生纵摇的同时一定会发生垂荡。本文并未分析垂荡纵摇的强耦合性对运动的影响,所以在今后研究中有待进一步改进。
