基于动态贝叶斯网络的无人机航迹模型研究*

张 健,罗鑫悦,黎宗孝,赵嶷飞

(中国民航大学 空中交通管理学院,天津 300300)

0 引言

当前,无人驾驶航空业正不断快速发展、迭代演进。在人工智能等全新技术革命为主的第四次工业革命浪潮中,无人驾驶航空应运而生并蓬勃发展,已成为先进生产力的重要载体。随着在农业、物流、航拍乃至载人等通用和运输航空领域的推广应用,无人驾驶航空正在逐步融入国家空域系统。从行业细分市场来看,我国消费级无人机预计2024年市场规模将达到568亿元,工业级无人机预计2024年市场规模达到1 508亿元[1]。

然而,与无人机数量急剧增长的态势相比,无人机管理规范与法律建设明显滞后。中国民航局、JARUS、FAA、EASA相继发布监管规则[2-6]。将小型无人机的运行空域限制为120 m以下,以避免干扰有人机运行。该规则要求小型无人机必须在飞手视距内或在具有有效通信能力的观察员视距内运行。Thomas等[7]、Jeffrey等[8]分别介绍以部分国家为代表的无人机主流运营机构,设想通过空域和航路设计等实现无人机超视距运行,构建无人机空管系统。参照有人机在空中运行安全领域的发展路径,对无人机安全管理而言,无人机空管系统建设的关键和难点在于开发类似于有人机配备的机载防撞系统的无人机冲突探测与解脱(conflict detection &resolution,CDR)技术;作为CDR的前提,航迹预测模型研究成为核心课题[9]。

CDR技术在有人机领域开展比较早,很多学者均在这方面做出过很多研究。James[10]结合美国林肯实验室在机载防撞系统研发方面积累的经验,对有人机航迹预测及CDR建模方法进行了系统总结。然而对于小型无人机航迹预测的研究,国内外均处于起步阶段,主流方法包括基于运动学模型以及机器学习2种方法。

1)基于运动学模型

Vinay等[11]使用适用于有人机的BADA(base of aircraft data)模型对无人机航迹建模,生成无人机航迹预测的性能参数,发现轻型、电动或垂直飞行无人机对模型适用性不足。Chen等[12]针对多无人机协同跟踪多无人机编队问题,提出了1种分散式协同跟踪控制方法。James等[13]证明了无人机差异性对航迹建模误差具有非常大的影响。D’Souza等[14-15]提出1种广义六自由度多旋翼无人机航迹模型,用于有风状态下无人机性能识别。

2)基于机器学习

Alligier等[16]提出1种基于机器学习的方法来学习无人机的运行因素,改进了无人机爬升预测的准确性。Wang等[17]提出1种基于飞行模式识别的混合方法。James等[18]利用神经网络学习无人机视觉特征,提出1种新的无人机探测方法。赵嶷飞等[19]从无人机运行状态角度,实现航迹的状态预测。李亦同[20]利用马尔可夫过程,基于历史数据进行航迹预测方法研究。陆佳欢等[21]使用长短期记忆神经网络算法和历史数据进行训练,提出无人机实时航迹预测算法。

综上可知,针对无人机的航迹预测问题,已有研究均存在不足之处。无人机的机型种类繁多,且存在大量自行开发组装,性能参数各不相同,加之制造商不愿公布参数,采用质点运动模型进行无人机航迹预测,研究中缺乏完整的无人机性能手册。基于无人机历史航迹数据,采用机器学习类方法进行航迹预测成为必然之举。然而已有聚焦于历史航迹数据的模型,存在预测长度和精度之间难以平衡的问题,仅用于短期预测。

鉴于此,本文采用贝叶斯网络作为底层方法。首先,基于经验模型构建了无人机航迹变量之间的静态贝叶斯网络和动态贝叶斯网络。之后,统计历史航迹离散化数据,确定贝叶斯网络中各个子节点变量的条件概率矩阵并进行降维存储。最后,基于动态贝叶斯网络,编程调用条件概率矩阵并反复迭代,最终实现航迹预测。

1 航迹模型的分析

1.1 航迹模型变量

航迹数据包含的变量很多,且变量间存在多重耦合,例如,城市物流无人机低空飞行比高空飞行时速度要小得多、高速飞行比低速飞行时转弯率要小得多。结合航迹预测功能的需要,涉及的主要变量是:高度数据、飞行速度、加速度、升降率和转弯率。基于当前城市物流无人机航迹数据,一般可以直接得到高度、速度,而加速度、转弯率和升降率则需要推导获取。

1)加速度变量。速度可以直接获得或加速度分量整合获得,通过对速度变量做差得到加速度数值。

2)升降率变量。通过无人机前后时刻高度变化获得。

3)转弯率变量。通过无人机航向前后时刻变化得到,或通过速度分量比值推导间接获得。

1.2 航迹模型功能

贝叶斯网络作为1种概率图模型,已在民航安全评估领域进行不少应用。本文将贝叶斯网络模型引入无人机航迹预测问题研究。首先,基于无人机性能和专家经验,构建静态贝叶斯网络和动态贝叶斯网络。接着,对无人机历史航迹数据进行离散化处理,以训练和构建变量间条件概率矩阵。最后,通过预测数据的连续化和可视化处理,实现航迹预测功能。

2 贝叶斯网络模型构建

2.1 贝叶斯网络概述

贝叶斯网络(Bayesian network,BN)被称为因果概率网络,基础是贝叶斯公式。贝叶斯网络各节点变量的条件概率是在贝叶斯公式与统计学的基础上发展而来。设x1,x2,x3,…,xn,是变量X的1个互不相容的完备事件组,且p(xi)>0,Y是X引发的事件,贝叶斯公式如式(1)所示:

(1)

式中:xi为变量X的某个事件;xj为变量X的某个事件;p(xi)为事件xi的发生概率;p(Y|xi)是xi引发Y事件的条件概率。

动态贝叶斯网络模型以离散变量集为研究对象,满足马尔科夫特性和平稳特性。动态贝叶斯网络可以看作是应用贝叶斯统计思想结合动态结构的模型,既能够体现变量之间的概率依存关系,又能描述这一系列变量随时间变化的情况,是贝叶斯网络在时间变化过程上的扩展。动态贝叶斯网络作为1种机器学习方法,已被广泛应用于语音识别、地面交通轨迹数据挖掘等领域。

2.2 初始贝叶斯网络航迹模型

贝叶斯网络将每个变量视为节点,用有向边表示它们之间的条件概率依赖关系,如图1所示。

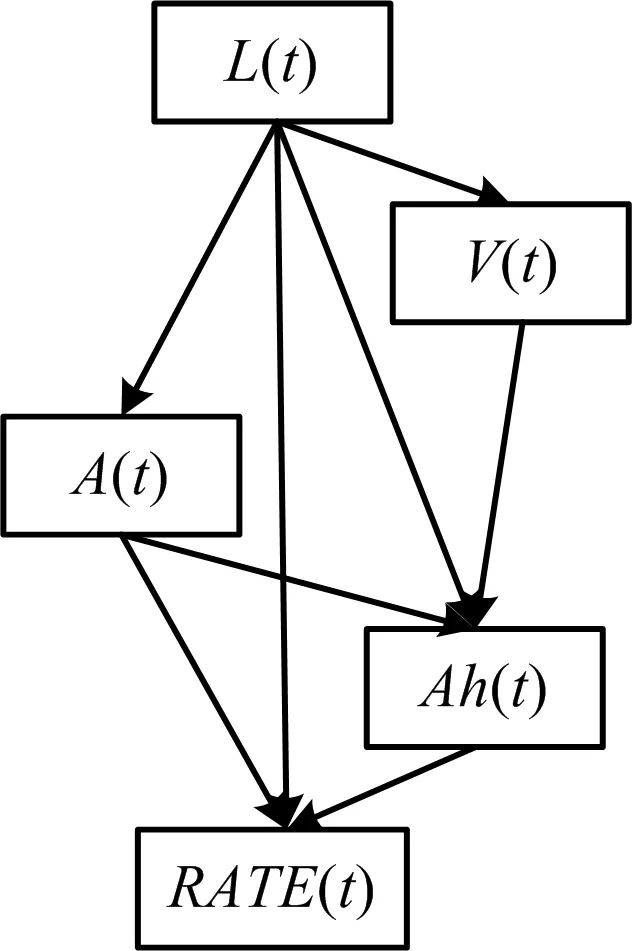
注:L(t)为t时刻高度,m;V(t)为t时刻速度,m/s;A(t)为t时刻加速度,m/s2;Ah(t)为t时刻升降率,m/s;RATE(t)为t时刻转弯率,(°/s)。图1 航迹预测中的静态贝叶斯网络递推关系Fig.1 Recursive relationship of static Bayesian network in track prediction

由图1可知,该网络模型基于航空器性能参数模型和经验模型汇总得来,同时借鉴有人机在航迹预测模型中的参数关系。以升降率Ah(t)为例,影响其取值的父节点包括高度L(t)、速度V(t)、加速度A(t)。

2.3 动态贝叶斯网络模型航迹

动态贝叶斯网络背后的假设是,系统的下一个状态只取决于当前状态,也被称为马尔可夫假设。基于航空器性能和专家经验,同时也借鉴有人机在航迹预测模型中的参数关系,得出如下动态贝叶斯网络航迹模型,如图2所示。

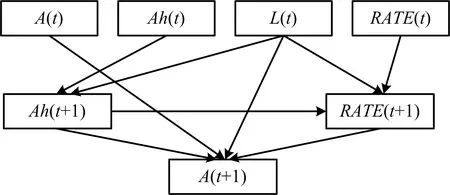
图2 航迹预测中的动态贝叶斯网络递推关系Fig.2 Recursive relationship of dynamic Bayesian network in track prediction

由图2可知,给定当前时刻高度、加速度、升降率、转弯率4个变量值,根据动态贝叶斯网络及各个变量的条件概率矩阵,即可实现下一时刻航迹预测和生成。

3 航迹数据与模型训练

3.1 航迹数据

历史航迹数据是变量取值的出处,也是进行模型训练的基础。本文基于贝叶斯网络的模型求解数据,来自2021年5月10日-2021年5月16日期间,顺丰无人机于江西省赣州市某配送航线运行记录。经统计,日约26 000条,合计182 511条航迹数据。其中,每天存在约15航次飞行活动,飞行活动涵盖离场上升、巡航、下降着陆3个阶段。执行每次飞行活动的无人机机型为Ark方舟无人机或H4四旋翼无人机2款。论文所采用的某城市物流无人机航迹数据格式如表1所示。

表1 无人机航迹数据格式Table 1 UAV track data format

基于前文航迹变量介绍,高度变量可以直接获取,速度、加速度、转弯率和升降率则通过推导获得。

1)速度和加速度变量

速度通过已知速度分量整合获得,如式(2)所示:

(2)

式中:VE(t)为东向速度,m/s;VN(t)为北向速度,m/s;VG(t)为地向速度,m/s。

对前后2个时刻速度做差获取加速度数值,如式(3)所示:

A(t)=V(t+1)-V(t)

(3)

2)升降率变量

通过对无人机前后2个时刻高度数值做差获得,如式(4)所示:

Ah(t)=L(t+1)-L(t)

(4)

3)航向角和转弯率变量

将东向速度与北向速度做比,得到航向参考数据。设定北为Y轴正方向,东为X轴正方向,将将航向参考数据转化为大地坐标系下航向角,如式(5)所示:

(5)

式中:θ(t)为无人机在大地坐标系航向角,(°)。

若VE(t)>0,VN(t)>0,则θ(t)=θ(t);若VE(t)<0,VN(t)>0,则θ(t)=360°-θ(t);若VE(t)>0,VN(t)<0,则θ(t)=180°-θ(t);若VE(t)<0,VN(t)<0,则θ(t)=180°+θ(t)。

进而计算转弯率,如式(6)所示:

RATE(t)=θ(t+1)-θ(t)

(6)

3.2 基于贝叶斯网络的条件概率矩阵训练与存储

3.2.1 条件概率矩阵的训练

基于贝叶斯网络模型要求,对变量历史数据取值进行离散化,并将这些量化区间用序号命名。例如,将高度划分为[100,140)、[140,180)、[180,220)、[220,260]4个区间。针对高度、速度、加速度、升降率、转弯率离散值,运用历史数据统计和训练,生成各节点变量的条件概率矩阵。过程为:

1)针对不同机型,分别筛选出各自飞行活动所产生的航迹数据,用于后续分别针对特定机型的航迹数据训练。

2)针对贝叶斯网络中的每个变量取值,基于数据分布情况分别定义一系列的分割点c1c2…cn对变量数据进行量化。数值小于c1的量化到第1个区间,大于cn的量化到第n+1个区间,以此类推,各个变量分别被量化为1至n+1的离散值。

3)针对某型无人机每次航线飞行活动航迹数据,基于贝叶斯网络中变量间约束条件,分别统计各种约束关系下的出现次数。以转弯率为例,动态贝叶斯网络中的当前时刻转弯率受到上一时刻高度(4个离散值)、当前时刻升降率(4个离散值)、上一时刻转弯率(5个离散值)3个变量约束和决定,要分别针对各组合情况统计当前时刻转弯率取值概率情况,生成条件概率矩阵。

4)针对该型无人机的每次航线飞行活动,分别进行第3步操作,并以之对同型航空器当天其他飞行航次进行预测。选取预测效果最匹配的1次条件概率矩阵,作为当天的条件概率矩阵。

动态贝叶斯网络里的转弯率概率矩阵部分样例展示如表2所示。

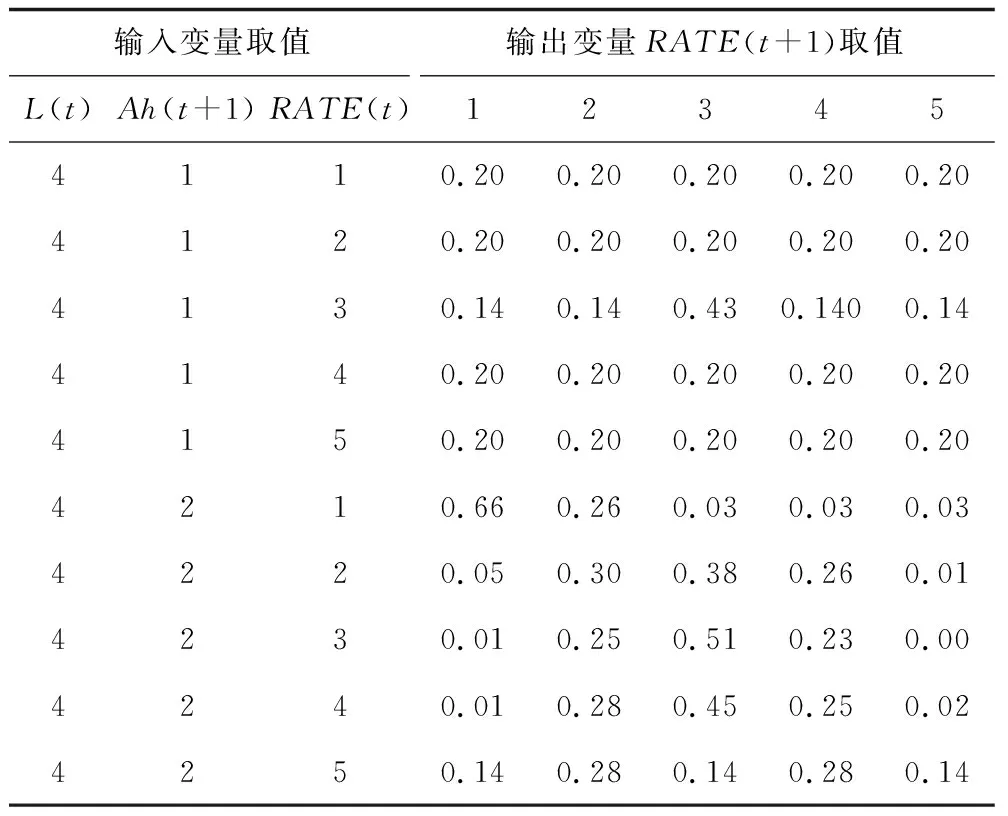
表2 转弯率条件概率矩阵Table 2 Conditional probability matrix of RATE

3.2.2 条件概率矩阵的存储

多重变量条件概率矩阵非常庞杂,为有效存储和调用,提出了多维矩阵降维方法。首先,建立空白矩阵,列数由该变量离散量化区间数决定,行数由其父节点个数和各自离散量化区间数决定。以转弯率的条件概率矩阵存储为例,行数设定时,将上一时刻高度取值定义为百位,将当前时刻升降率取值定义为十位,将上一时刻转弯率取值定义为个位。结合各节点区间个数,确定行数为445行,列数为5列。之后将条件概率矩阵中的每一行概率值导入特定行中,取值范围之外数据做空白处理,如表3所示。

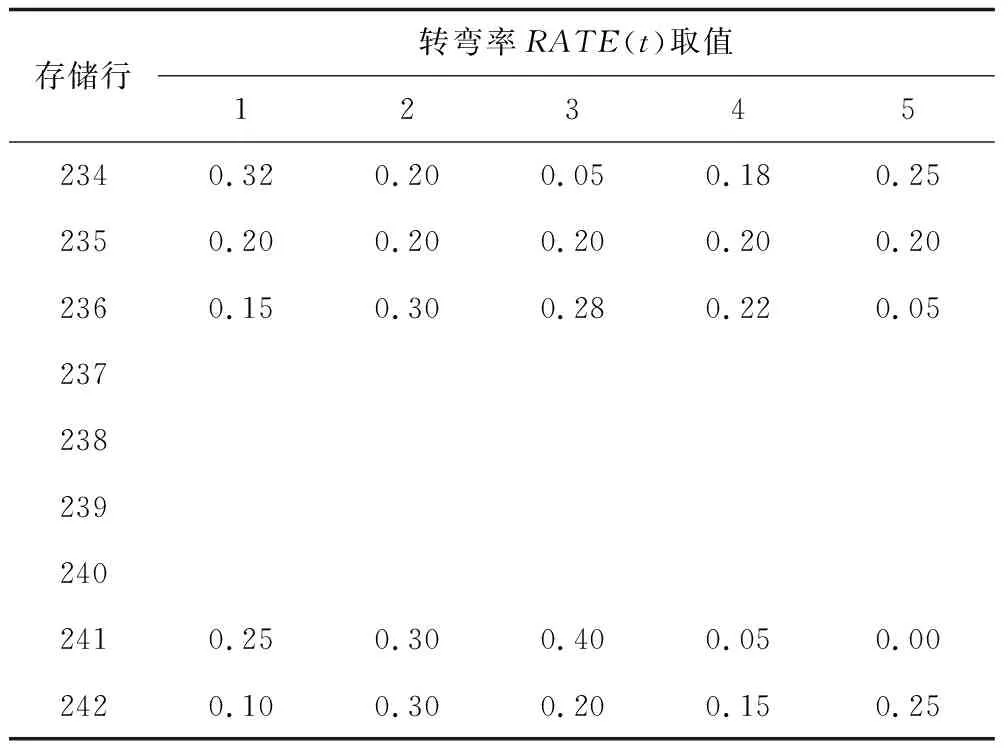
表3 转弯率条件概率矩阵存储格式Table 3 Storage format for conditional probability matrix of RATE

针对无人机升降率、转弯率和加速度,均可建立类似条件概率矩阵。在之后迭代过程中,通过调用变量条件概率矩阵,依照子节点取值概率分布生成预测值。

4 航迹模型预测结果

4.1 预测数据的连续化

通过初始贝叶斯网络和高度初始数据,动态贝叶斯网络中的高度、加速度、升降率、转弯率均获得初始数据,之后在每轮迭代中生成加速度、升降率和转弯率的预测值。在此过程中,高度没有参与预测,需要由升降率新值连续化,更新高度原值生成高度新值,再对高度信息进行离散化,以驱动下一轮预测过程。

预测结束后,需要将升降率、加速度、转弯率的离散值进行逆向连续化处理。直接进行连续化处理,会导致随机取值的波动性过大,毛刺化严重。为此,本文提出1种连续化重复采样方法,即如果离散值在一段时间内始终不变,则只取其对应量化区间内同一随机数值。其中,若量化区间内存在0值,则取0作为该时段数值。以升降率逆向连续化为例进行展示,如图3所示。

图3 升降率连续化重复采样Fig.3 Repeated continuous sampling of Ah

由图3可知,连续化处理可以最大程度降低毛刺现象。上述处理后,将升降率、加速度依次叠加到高度和速度变量上,间接完成高度和速度的连续化,如式(7)～(8)所示:

L(t+1)=L(t)+Ah(t+1)

(7)

V(t+1)=V(t)+A(t+1)

(8)

4.2 预测数据的可视化

针对预测得到的无人机航迹数据,进行可视化处理,建立三维坐标系。其中,Z轴取值地面垂直向上为正,X轴取值向东为正,Y轴取值向北为正。在XY平面上,设定航向初始值,将预测出来的转弯率变化量不断叠加,迭代生成航向新值。基于运动学方程,生成无人机在X轴、Y轴、Z轴的实时位置,如式(9)～(12)所示:

x(t+1)=x(t)+V(t)cosθ(t)

(9)

y(t+1)=y(t)+V(t)sinθ(t)

(10)

z(t)=L(t)

(11)

(12)

式中:x(t)为无人机在X轴坐标;y(t)为无人机在Y轴坐标;z(t)为无人机在Z轴坐标;θ0为无人机初始航向。

预测航迹与历史数据对比如图4所示。

图4 预测航迹和真实航迹对比Fig.4 Comparison between predicted track and real track

从图4可知,预测航迹与真实航迹相似度很高。对预测效果进行分析,如表4所示。

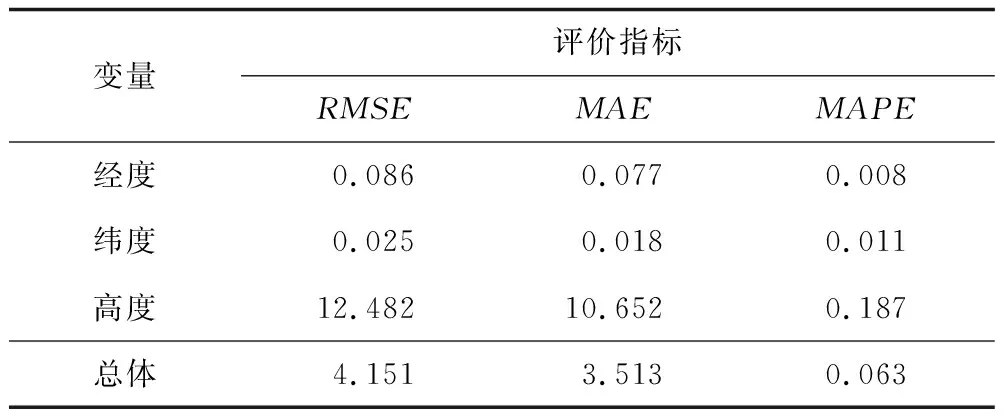
表4 航迹模型的预测性能Table 4 Prediction performance of track model

由表4可知,基于动态贝叶斯网络的无人机航迹预测数值与真实航迹数据总体符合性较好,总体预测精度接近94%。但航迹对比图显示部分航段符合度不够高,进一步数据分析也验证这个观察。

5 结论

1)本文首次将动态贝叶斯网络引入城市物流无人机航迹预测研究中,构建无人机航迹模型,完成无人机航迹变量多个离散取值的动态迭代和预测,最终实现无人机航迹预测功能。

2)数据量化处理和逆向连续化采样存在近似处理,数据离散化处理时存在量化区间数量确定上的不足,后续通过收集更多的无人机运行数据加密量化区间。此外,由于每次对变量离散预测值的连续化采样具有随机性误差,进而导致推导出的高度、速度、航向存在误差,后续考虑通过优化重复采样方法降低该误差。

3)不同飞行阶段和不同型号无人机预测效果存在差异。因无人机不同飞行阶段展示的机动差异,使得预测航迹在上升转入巡航阶段存在较大误差,后续需要针对城市物流无人机不同飞行航段,分别进行精细化预测。此外,文中航迹预测模型是基于同型无人机构建,换言之,不同型无人机需要分别构建预测模型。当前物流运输无人机航线飞行是在飞控系统控制下自动飞行,因此可基本排除人为操作习惯引起的差异。大风等天气也会对无人机飞行航迹保持造成影响,因此,论文中针对不同自然日,分别进行模型训练和构建。后续研究可融入天气因素,完善模型预测效果。

4)本文提出的无人机航迹模型,作为1种普适性航迹预测方法,可以实现针对任意航线、任意机型的航迹预测。随着飞行活动增加,必然会打破当前无人机航线隔离划设的现状。因此,实现特定航线、特定机型的航迹预测,可为不同型号无人机之间交叉运行时冲突探测和解脱技术提供基础。