基于POA-ELM 的含煤地层异常构造分类
2023-12-11赵雯宇王元军
高 洁 , 伊 雨 , 赵雯宇 , 王元军 , 王 亮
(1.山东科技大学 电子信息工程学院, 山东 青岛 266590;2.中天合创能源有限责任公司, 内蒙古 鄂尔多斯 010300;3.山东科技大学 机械电子工程学院, 山东 青岛 266590)
煤矿事故的发生会造成大量的人员伤亡和巨大的经济损失,煤层异常构造的存在会增加煤矿事故发生的概率[1],因此含煤地层异常构造识别研究对提高煤矿开采的安全性十分重要。槽波地震勘探作为一种极具发展前景的地球物理勘探方法,不仅能够有效探测陷落柱、小断层等,同时对采空区及废弃巷道等探测效果也较显著[2]。该技术具有探测精度高、距离大、波形特征易于识别、抗干扰能力强等优势[3],尤其在探测精度和距离方面优于其他煤矿井下物探方法[4],近年来被广泛应用[5-7]。
槽波地震数据的处理与解释是槽波地震勘探的重要一环,目前常用的方法有层析成像、偏移成像等成像法[8-11],通过成像能直观地确定构造的种类和位置,但数据处理与成像过程繁杂,耗时耗力,并且成像结果多依靠人工经验解释,易出现偏差,此外,共中心点叠加法、速度分析法也常用于处理槽波数据[12-14],但多与成像技术结合,同样易出现偏差。近些年,机器学习也被应用到地震勘探领域[15],通过地震数据识别异常地质构造,但多以识别断层为主[16-19],在其他构造识别方面研究较少。
极限学习机(ELM)是由HUANG 等[20]于2004年提出的一种单隐含层前馈神经网络,与传统训练算法相比,ELM 具有设置参数少、学习速度快、训练误差小以及泛化性能好等优势[21-23],但由于ELM 的输入权值与隐含层偏置是随机产生的,导致分类性能不稳定[24-26];鹈鹕优化算法(POA)是2022 年由Pavel Trojovsky 和Mohammad Dehghani 提出的,是一种模拟鹈鹕群体狩猎的智能优化算法,其在逼近最优解方面具有较强的挖掘能力,并且不易陷入局部最优[27],能够为极限学习机寻到最优的输入权值与隐含层偏置,经过优化后的极限学习机更加适合处理数量庞大、包含信息复杂的槽波数据,可以更好地完成煤层构造的识别分类任务。因此,笔者提出基于POA-ELM 的含煤地层构造识别分类方法,对小断层、冲刷带和陷落柱进行识别分类研究,并对分类结果进行评价与分析。
1 方法原理
1.1 极限学习机
与传统的前馈神经网络不同,ELM 未采用基于梯度的算法,而是随机选择输入权值和隐含层偏置[28-29],并根据最小二乘准则,依据Moore-Penrose 广义逆矩阵理论求出输出权值[30]。xin]T∈Rn,ti=[ti1,ti2,···,tim]T∈Rm,n为输入层节点数,
假设有N个任意样本(xi,ti),其中xi=[xi1,xi2,···,m为输出层节点数,中间有L个隐含层,第k个隐含层节点的输出为hk(xi),可表示为
式中,wk=[ωk1,ωk2,···,ωkn]T为输入节点与第k个隐含层节点的输入权值向量;bk为第k个隐含层节点的阈值;wk·xi为wk和xi的内积;g(wk,bk,xi)为激活函数。
ELM 原理如图1 所示。ELM 的学习目标可转化为使输出误差最小,即存在βk、wk和bk,使得

图1 极限学习机原理Fig.1 Principle diagram of extreme learning machine
式中,βk=[βk1,βk2,···,βkm]T为第k个隐含层节点与输出层节点的输出权重向量;yi为第 个样本对应的模型输出。
式(2)用矩阵表示为
其中,H为隐含层节点的输出矩阵;β为隐含层与输出层连接权重矩阵;Y为期望输出矩阵。式(3)展开形式为
通常将期望输出矩阵Y与样本标签T求残差最小平方和作为评价目标函数,使该目标函数最小的解就是最优解,目标函数可表示为
通过线性代数和矩阵理论的知识推导得出式(6)的最优解为
式中,H†为矩阵H的Moore-Penrose 广义逆矩阵。
1.2 鹈鹕优化算法
鹈鹕优化算法模拟了鹈鹕在狩猎过程中的自然行为,每个种群成员代表一个候选解。鹈鹕种群初始化数学描述为
式中,qu,v为第u个鹈鹕的第v维位置;M为鹈鹕的种群数量;r为求解问题的维度,即待优化变量的个数;rand为 [0,1] 内的随机数,dv和lv分别为求解问题的第v维的上、下边界。
鹈鹕种群可用种群矩阵表示,即
其中,Q为鹈鹕的种群矩阵;Qu为第u个鹈鹕的位置。鹈鹕的目标函数值可用目标函数向量表示为
其中,F为鹈鹕种群的目标函数向量;Fu为第u个鹈鹕的目标函数值。
鹈鹕的狩猎过程主要为逼近猎物和水面飞行,在POA 算法中,则主要分为勘探阶段和开发阶段。
(1)勘探阶段。
式中,Q为第u个鹈鹕的新位置;F为基于第1 阶段更新后的第u个鹈鹕的新位置的目标函数值。
(2)开发阶段。
2 含煤地层异常构造模型与槽波信号数据集建立
2.1 含煤地层异常构造仿真模型建立
笔者利用COMSOL Multiphysics5.5 仿真软件,分别建立小断层、冲刷带和陷落柱的三维含煤地层异常构造仿真模型,模型尺寸为100 m×10 m×10 m,上下围岩厚度均为4 m,煤层厚度为2 m,采用主频为200 Hz的雷克子波作为地震子波。在煤层中激发后,检波器会接收到携带各构造信息的槽波信号。三维等效介质模型参数见表1,模型结构如图2 所示,为了更好的模拟实际煤层,避免模型表面边界发生反射现象影响仿真结果的准确性,在3 种构造模型中均设置了低反射边界。

表1 3 种仿真模型物性参数Table 1 Physical parameters of three simulation models

图2 3 种构造仿真模型Fig.2 Simulation model of three structures
2.2 槽波模拟与数据处理
笔者采用槽波地震勘探中的透射波法[31],分别采集小断层、冲刷带、陷落柱的槽波信号。将震源激发点置于模型x=0 的中央处,在模型x=100 m 处共设置606 个检波器,检波器在模型中的位置如图3 所示,所有检波器在x=100 m 处的排列如图4 所示,图4 中每条红色线由101 个检波点排列形成,红色线间距均为3 m,6 条红色线共排列606 个检波点,检波点间距为0.1 m,坐标见表2,Range(2,3,10)表示在y方向检波器位于从2~10 m 以3 m 为步长取点处。

表2 检波器位置坐标Table 2 Position coordinates of the detector

图3 检波器位置示意Fig.3 Schematic diagram of the position of geophones

图4 检波器布置示意(x=100 m)Fig.4 Schematic diagram of geophones(x=100 m)
每种构造模型采集到606 个槽波数据样本,3 种构造模型共得到1 818 个样本,每个样本为时长0.2 s的时序数据,包含501 个采样点,得到1 818×501 的样本数据,如图5 所示,3 种模型的槽波信号能量都集中于0.05~0.10 s,但每类信号的轮廓与幅值具有明显差异,这为实现3 种构造模型的分类提供了可能。

图5 槽波样本数据Fig.5 In-seam wave sample data
在利用极限学习机处理分类问题时,数据的预处理效果直接关系到模型的分类效果。采集到槽波数据后,首先对其进行z-score 标准化,消除由不同量纲与数值量级所引起的数据偏差,使得数据具有可比性。最后采用主成分分析法(PCA)对标准化后的数据进行降维,消除冗余数据,提高分类模型的训练速度,同时也尽可能保留各数据的原始特征,保证分类结果的准确率。PCA 降维时,若第p个特征贡献率接近于1,则选取前p个主成分代替原来的槽波数据。特征累计贡献率情况如图6 所示,第30 个特征贡献率达0.998 5,因此选取前30 个特征,最终将501 个数据特征降为30 个数据特征,得到1 818×30 的样本数据。

图6 特征累计贡献率Fig.6 Cumulative contribution rate of characteristics
3 基于POA-ELM 的煤层异常构造分类模型建立
3.1 传统极限学习机分类模型建立
笔者对极限学习机分类模型的激活函数、隐含层节点数进行研究。如图7 所示,通过比较分类准确率,选择最佳激活函数和隐含层节点数,实验结果表明:随着隐含层节点数的增多分类准确率总体趋势也增高,能够明显看出,当激活函数为Sigmoid 函数或Hardlim 函数时,分类准确率远高于Tribas 函数和Radbas 函数。当隐含层节点数设为20、激活函数设为Sigmoid 函数时,ELM 分类准确率达到了最大值95.24%,隐含层节点数大于20 时分类准确率趋于平稳。根据以上分析,笔者将Sigmoid 函数作为极限学习机分类模型的激活函数,隐含层节点数设置为20。

图7 隐含层节点与激活函数的选择Fig.7 Selection of hidden layer nodes and activation function
3.2 鹈鹕算法优化的极限学习机模型
基于前文的ELM 分类模型,利用鹈鹕优化算法对极限学习机进行优化,在有限的迭代次数里,找到使得ELM 分类效果最佳的输入权值和隐含层偏置,从而弥补ELM 因随机生成输入权值和隐含层偏置导致分类效果不稳定的缺点,提高分类模型性能,优化过程如图8 所示。将极限学习机的分类准确率作为鹈鹕优化算法的适应度函数,进行数次迭代,比较适应度值,不断更新鹈鹕位置,并保存目前最优输入权值与隐含层偏置。笔者将鹈鹕种群数量设置为30,最大迭代次数设置为100,迭代过程如图9 所示,当迭代次数为37 时,POA 为ELM 寻到全局最优解,收敛速度较快。
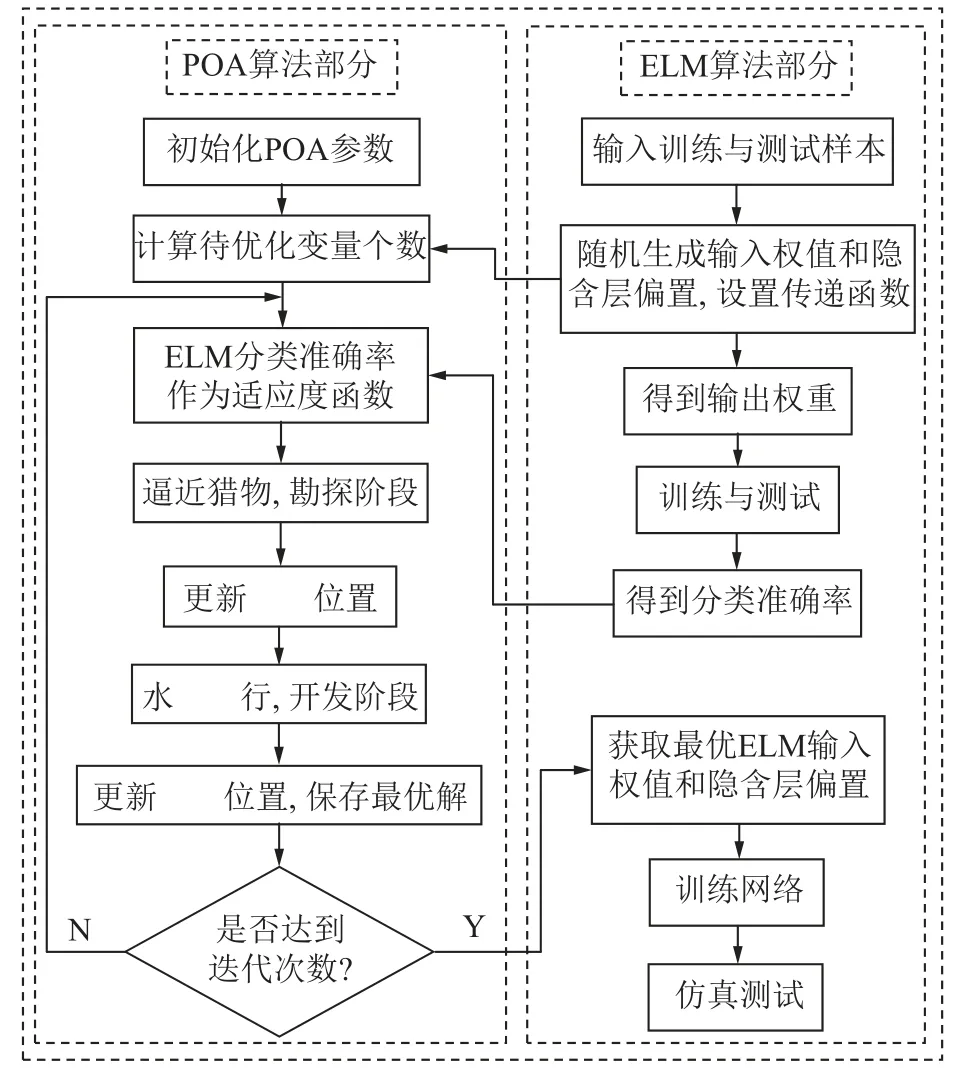
图8 鹈鹕算法优化极限学习机Fig.8 Flowchart of pelican optimization algorithm optimizing extreme learning machine

图9 POA 寻优迭代过程Fig.9 POA optimization iterative process
4 测试结果与分析
4.1 分类结果与分析
实验中随机选取70%的样本数据作为训练集,剩余30%个样本数据作为测试集,将小断层标签设为1,冲刷带标签设为2,陷落柱标签设为3。ELM 测试集的分类结果如图10 所示,分类准确率为95.238 1%,共有26 个样本被分类错误。POA-ELM 测试集的分类结果如图11 所示,分类准确率达99.450 5%,共有3 个样本被分类错误,从准确率和错误分类样的本分布情况来看,POA-ELM 分类效果优于传统ELM。

图10 ELM 分类结果Fig.10 Classification result of ELM

图11 POA-ELM 分类结果Fig.11 Classification result of POA-ELM
前文通过准确率对整体分类效果进行了分析,下面通过精确率(P)、召回率(R)2 个评价指标,对ELM和POA-ELM 的分类结果进行评价和对比,P和R均是针对每类模型的分类结果进行评价。将ELM 和POA-ELM 分类结果的P和R整合为如图12 所示,ELM 各模型的P和R指标均大于93%;POA-ELM各模型的P和R指标均在99%以上,POA-ELM 分类效果明显优于传统ELM,分类效果较为理想。

图12 分类结果评价指标Fig.12 Evaluation index of classification results
为消除数据集分布带来的分类性能波动,笔者采用十折交叉验证评估分类模型的性能,将1 818×30 的样本数据集和1 818×1 的标签数据集打乱顺序并均匀分为10 份,依次选取其中1 份作为测试集,其余9 份作为训练集,每份数据均作为测试集后,完成1 次十折交叉验证,取均值作为1 次十折交叉验证的结果。将以上过程重复10 次,结果如图13 所示,经验证传统ELM 分类准确率波动较大,而POA-ELM 基本保持平稳状态,且分类准确率均保持在99%左右,说明本文构建的POA-ELM 分类模型对于含煤地层异常构造识别分类具有稳定且良好的分类性能。
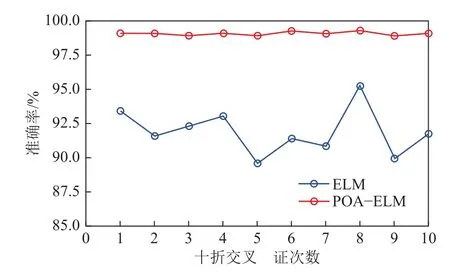
图13 十折交叉验证结果Fig.13 Result of ten-fold cross validation
4.2 POA-ELM 的实际应用
为说明本文构建的POA-ELM 模型对实际构造的分类性能,将长城五号矿1901N 工作面的槽波地震勘探数据引入测试集进行分类。1901N 工作面中槽波观测系统如图14 所示,在1901N 运输巷布置53 个炮点,1901N 回风巷布置61 个接收点,采用透射法勘探,得到2 个异常区YC1 和YC2(图14 洋红色线圈定的范围),经分析YC1、YC2 异常区均为贯穿工作面的断层影响区。选取P1-34~P1-36三炮槽波数据用于实际断层的识别,共183 组槽波数据样本,为保证POA-ELM 模型对实际断层的识别效果,与仿真槽波数据中断层测试集样本量一致,将P1-36炮中包含断层信息较少的第61 组槽波数据剔除,剩余182 组作为识别实际断层的测试集样本,如图15 所示。为保证分类速度与准确率,首先对三炮断层槽波进行4 层小波去噪,去噪前后的槽波如图16 所示,去噪之后波形噪声有所减少,进而对其进行z-score 标准化和PCA降维,得到182×30 的断层测试集数据。182 组断层槽波数据经过数据预处理后,将代替原本的仿真断层测试集数据进行识别分类。

图14 槽波观测系统示意Fig.14 In-seam wave observation system diagram

图15 P1-34 至P1-36 炮槽波时间-振幅Fig.15 Time-amplitude diagram of P1-34 to P1-36 shot in-seam wave

图16 原始槽波数据与去噪槽波数据对比Fig.16 Comparison of original in-seam wave data and denoised in-seam wave data
分类结果如图17 所示,整体分类准确率为97.435 9%,与图11 仿真分类结果相比,准确率有所下降,小断层被错误分类的数据有所增多。结合图18混淆矩阵分析,有4 组断层数据被错误分类为冲刷带,8 组被错误分类为陷落柱,小断层召回率为93.4%,相对于图12 召回率下降6.1%,准确率和小断层召回率下降的主要原因是相对于仿真槽波数据,实际槽波会含有部分残留噪声,且与训练集的仿真数据特征存在差别。总体来看,准确率、召回率及精确率均高于93%,分类结果较为理想,说明本文构建的POA-ELM 模型能够有效分类实际槽波数据,实现地质构造的分类识别。

图17 POA-ELM 实际数据分类结果Fig.17 POA-ELM classification result of real data

图18 实际数据分类混淆矩阵与评价指标Fig.18 Confusion matrix and evaluation index of real data
4.3 不同方法分类结果对比
基于相同的样本数据,分别采用支持向量机(SVM)和BP 神经网络2 种方法对含煤地层异常构造进行识别分类,分类结果如图19 所示,对于仿真数据4 种方法的分类准确率都达到了90%以上,其中POA-ELM 和SVM 的准确率都达到了97%以上;对于含断层的槽波数据POA-ELM 的分类准确率达97.44%,高于其他3 种方法。综合分析,无论是仿真槽波数据还是含实际断层槽波数据,笔者提出的POA-ELM 分类模型都更具优势。

图19 分类结果对比Fig.19 Comparison of classification results
5 结 论
(1)提出了一种鹈鹕优化算法优化的极限学习机分类模型POA-ELM,利用鹈鹕优化算法对极限学习机的输入权值和隐含层偏置进行寻优,提高了极限学习机分类模型的分类准确率和稳定性。
(2)将POA-ELM 分类模型应用到含煤地层异常构造识别分类中,通过建立含煤地层仿真模型,对断层、冲刷带和陷落柱模型进行了识别分类,取得了良好的分类效果,分类准确率达99%以上,分类性能更稳定,效果远优于原始ELM,证明了POA 对ELM 的良好优化效果和POA-ELM 在含煤地层异常构造识别分类中应用的可行性。
(3) POA-ELM 模型对于实际断层的识别准确率达97%以上,识别效果较为理想。与ELM、SVM、BP 的分类结果进行对比,无论是仿真槽波数据还是含实际断层槽波数据,POA-ELM 的分类识别准确率都最高,更具优势。
由于实际槽波数据资源有限,本文只对实际断层进行了识别,今后将对冲刷带、陷落柱等其他含煤地层异常构造进行识别,并进一步应用于槽波地震勘探。
